فرادرسمرجع تابع نمایی – به زبان ساده (+ دانلود فیلم آموزش گام به گام)
۱۹۶۸۷ بازدید
آخرین به‌روزرسانی: ۱۲ اردیبهشت ۱۴۰۲
زمان مطالعه: ۸ دقیقه
دانلود PDF مقاله
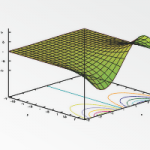
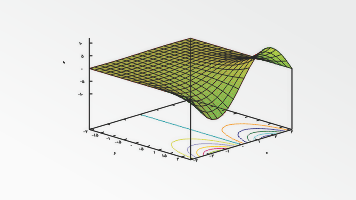
در این آموزش قصد داریم تا به تابع نمایی و خصوصیات آن بپردازیم.
فهرست مطالب این نوشته
فیلم آموزشی تابع نمایی
به تابع زیر تابع نمایی گفته می‌شود:
f(x) = ax
a هر مقدار بزرگتر از 1 است.
خصوصیات این تابع به مقدار "a" وابسته است.
- اگر a=1، نمودار یک خط افقی در y=1 می شود.
- غیر از این موضوع، دو مورد زیر پیش می‌آید:
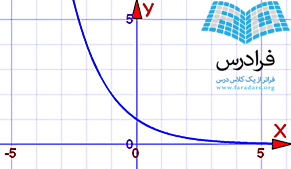
| اگر a بین 0 و 1 باشد
مثال: f(x) = (0.5)x در این حالت:
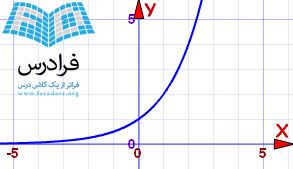
این تابع یک مجانب افقی مماس محور x ها دارد (y=0). | اگر a بزرگتر از 1 باشد
مثال: f(x) = (2)x در این حالت:
این تابع یک مجانب افقی مماس محور x ها دارد (y=0). |
در کل:
- این تابع همواره بزرگتر از " 0 " است، و هیچگاه محور x ها را قطع نمی کند.
- این تابع همواره محور y ها را در نقطه y=1 قطع می کند... به عبارت دیگر از نقطه (0,1) می گذرد.
- در نقطه x=1، f(x)=a... به عبارت دیگر از نقطه به طول 1 و به عرض a می گذرد.
- این تابع یک تابع یک به یک است.
- دامنه این تابع برابر اعداد حقیقی است:
- برد این تابع اعداد حقیقی مثبت است: (∞+,0)
معکوس
ax تابع معکوس logax است (تابع لگاریتمی).
پس تابع نمایی می‌تواند به وسیله تابع لگاریتمی "باز گردانده" شود.
تابع نمایی طبیعی
تابع زیر یک تابع نمایی "طبیعی" است:
f(x) = ex
که e همان "عدد اویلر" با مقدار تقریبی زیر است:
2.718281828459…
f(x) = ex نمودار
در نقطه به طول 1 و به عرض e شیب خط برابر e است و این خط مماس بر منحنی است.
اگر بازخوردی درباره این مطلب دارید یا پرسشی دارید که بدون پاسخ مانده است، آن را از طریق بخش نظرات مطرح کنید.
منابع:
mathsisfunدانلود PDF مقاله
https://b.fdrs.ir/2ii
مطالب مرتبط
سلام وقت بخیر جواب تابع ۲بهتوان x به اضافه ۲به توان x+۱ و نامدارش چگونه است
سلام.ببخشید برای a های منفی،چی؟
سلام وقت بخیر…
ببخشید یه سوال داشتم تابع رادیکال ۲ با فرجه x نمایی محسوب میشه ؟
با سلام و وقت بخیر؛
بله. اگر x2 را به فرم توانی آن و به صورت 2x1 بنویسیم، متغیر x در توان عدد مثبت 2 قرار می‌گیرد. این ساختار با فرم توابع نمایی همخوانی دارد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
سلام . نمودار تابع f(x)=a^x ( علامت ” ^ ” به معنی ” توان ” است ) که در آن ، a منفی است ، به شکل چند نقطه وصل نشده به هم ، است . پس در توابع نمایی ، از آن صرف نظر می شود .
چرا شیب تابع نمایی طبیعی برابر با e شده است لطفا توضیح بفرمایید با تشکر
سلام . دلیل برابر شدن شیب خط در یک معادله خط صاف ( که a ، نشان دهنده شیب خط است ) ، تانژانت زاویه حاصل بر محور x>0 و y>0 ( ربع اول دستگاه مختصات ) ، است . اما ما ، زاویه حاصل را ، نداریم . اما روش دیگری برای محاسبه ، وجود دارد . محاسبه شیب خط ، با دو نقطه انجام می شود . به طوری که a=(yA-yB)÷(xA-xB) . در اینجا ، a=(0-e)÷(0-1) می شود . در نتیجه ، a=(-e)÷(-1) که منفی در دو طرف تقسیم ، خط می خورد و در نتیجه ، a=e÷1 که در نهایت ، a=e می شود و شیب خط برابر e است . و y=ax+b است پس ، y=ex است . چون خط مبدا گذر است و b ( شیب خط ) ندارد ، و a=e است .
متد آموزش شما فوق العاده است.بی نهایت سپاسگزارم.
ببخشید من متوجه نمی شم که چرا پایه (a)نباید یک باشه
سلام . چون 1 یه توان هر عدد ، با 1 برابر است و خط y=1 ، نمودار این خط است .
سلام..چون اگر a برابر ۱ باشه به توان هر عددی که برسه میشه ۱ و درواقع خط y=1 نمودارش هست!
چون اگه 1 باشد به توان هرعددی بشه باز 1 میشه
سلام وقتتون به خیر منظور از متقارب به ایکس در جمله زیر چیست؟(lima^rn که در ان rnهر دنباله از اعداد گویا و متقارب به ایکس است.)
آموزش خوبی بود، ولی کافی نبود واقعا، بیشتر به درد دبیرستان میخورد و یادآوری، به هر حال متشکرم بابت محتوای خوب فرادرس..