اگزرژی (Exergy) در مکانیک — به همراه مثال

در مطالب مرتبط با ترمودینامیک، اصول این شاخه از مکانیک را معرفی کردیم. مفاهیم ارائه شده، به بررسی خاصیتی تحت عنوان آنتروپی پرداختیم و عنوان کردیم که هر فرآیند تنها در یک جهت اتفاق می‌افتد. در این مطلب اصطلاحی تحت عنوان «اگزرژی» (Exergy) را معرفی خواهیم کرد.

مقدمه

اصطلاح اگزرژی برای اولین بار توسط «Rant»، در سال ۱۹۵۶ ارائه شد. جایگزین دیگری که همین مفهوم را بیان می‌کند، «دسترس‌پذیری» نامیده می‌شود. دسترس‌پذیری، بیشترین کار قابل استخراج از سیستم را بیان می‌کند. اجازه دهید در ابتدا در مورد پیش‌نیاز‌های لازم به منظور درک اگزرژی صحبت کنیم.

فیلم آموزش بهینه سازی جریان اگزرژی Exergy در فرادرس

کلیک کنید

در ترمودینامیک می‌توان به هر سیستم، خاصیتی تحت عنوان انرژی داخلی نسبت داد که آن را با U نشان می‌دهند. با این فرض، قانون اول ترمودینامیک به صورت زیر بیان می‌شود:

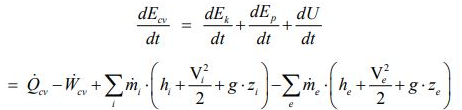
هم‌چنین به منظور توضیح قانون دوم برای یک سیستم، خاصیتی تحت عنوان آنتروپی تعریف می‌شود. این خاصیت از جنس میزان انتقال حرارت صورت گرفته در واحد دما است. با استفاده از آنتروپی می‌توان قانون دوم ترمودینامیک را در قالب فرمول زیر نشان داد.

در کتب مختلف این دو خاصیت را به شکل‌های گوناگونی بیان کرده‌اند. اما در حالت کلی می‌توان مفهوم آنتروپی و انرژی داخلی را به صورت زیر ارائه داد.

• انرژی داخلی بیان‌کننده انرژی جنبشی و پتانسیل یک سیستم در مقیاس میکرو است. برای مثال در مقیاس اتم‌ها و مولکول‌ها، این انرژی را می‌توان با استفاده از انرژی‌های ارتعاشی، دورانی و انتقالیِ آن‌ها توصیف کرد.
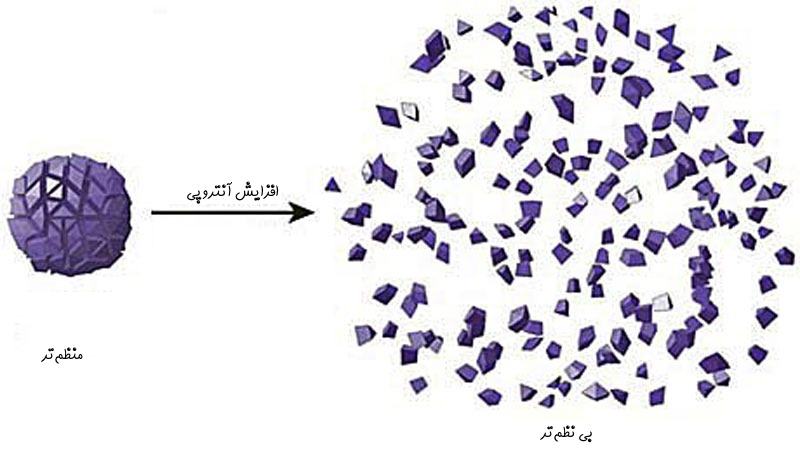
• آنتروپی معیاری از بی‌نظمی سیستم محسوب می‌شود. از دیدگاهی علمی‌تر، این خاصیت بیان‌کننده تغییرات تصادفی سیستم است. در سال‌های اخیر به جای بکار بردنِ اصطلاح «نظم و بی‌نظمی» از عنوان «ناتوانی سیستم در تولید کار» استفاده می‌شود.

اگزرژی را نیز می‌توان با همین روش توصیف کرد. «Szargut» از عبارت زیر به‌منظور توصیف اگزرژی استفاده کرده است.

«به میزان کار قابل استخراج از یک سیستم که طی فرآیندی برگشت‌پذیر به حالت تعادل ترمودینامیکی خود رسیده است، اگزرژی گفته می‌شود.»

این تعریف نشان می‌دهد که چطور کار ایده‌آلِ قابل استخراج از یک سیستم به خاصیت اگزرژی وابسته است. هم‌چنین لازم است بدانید که رابطه مشخصی میان آنتروپی تولید شده یک سیستم و اگزرژی وجود دارد. در حقیقت تولید آنتروپی برابر با میزان اگزرژی از دست رفته است. آنتروپی، ناتوانی سیستم در تولید کار و اگزرژی توانایی سیستم در تولید کار را نشان می‌دهد.

برای نمونه تصور کنید که مقداری آب ۵۰ درجه در اختیار دارید. فرض کنید کل انرژی موجود در آن برابر با ۵۰ کیلوژول است. به نظر شما چه تفاوتی میان کیفیت انرژی آب مفروض و ۵۰ کیلوژول برق وجود دارد. واضح است که شما با استفاده از برق می‌توانید هر کاری را انجام دهید اما با آب مورد نظر تنها می‌توان استحمام خوبی را تجربه کرد! در واقع کیفیت انرژی در دو سیستم متفاوت است. از این رو اگزرژی ۵۰ کیلوژول برق بیشتر از ۵۰ کیلوژول آب است.

کیفیت انرژی یا اگزرژی گرما

قبل از این‌که در مورد توصیف ریاضیاتی اگزرژی صحبت کنیم، مثال‌ زیر را در مورد میزان تبدیل گرما به انرژی مورد توجه قرار می‌دهیم.

فیلم آموزش ترمودینامیک ۱ در فرادرس

کلیک کنید

همان‌طور که قبلا نیز گفتیم، بیان کلوین-پلانک می‌گوید نمی‌توان از سیستمی کار گرفت، در حالی که تنها با یک منبع حرارتی مبادله انرژی دارد. در حقیقت این بیان به این معنی است که نمی‌توان تمامی حرارت یک سیستم را به کار تبدیل کرد. شکل‌های زیر دو حالتِ سیستمی را نشان می‌دهند که در یک سناریو، با یک منبع، تبادل حرارت دارد و در فرض دوم، با دو منبع مبادله انرژی می‌کند.

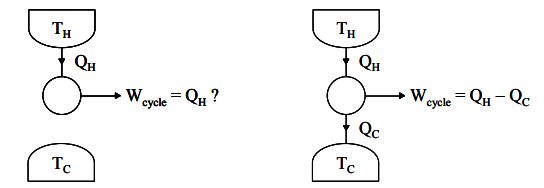
در حقیقت این بیان می‌گوید، سیستمی که با دو منبع حرارتی مبادله حرارت می‌کند، توانایی تولید کار تا سقف مشخصی را دارد. با توجه شکل‌های بالا قانون اول ترمودینامک را می‌توان به صورت زیر بیان کرد.

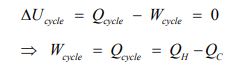
از طرفی قانون دوم بیان می‌کند که میزان کار استخراج شده از سیستم، در بازه زیر قرار دارد.

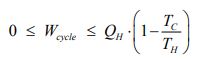
معادله بالا بیان کننده راندمان کارنو است که در حقیقت نشان‌ دهنده بیشترین کار خروجی ممکن از سیستمی محسوب می‌شود که بین دو منبع حرارتی کار می‌کند. بنابراین آن را می‌توان به صورت زیر تعریف کرد.

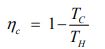
حال تصور کنید که منبعی با انرژی Q و دمای T در اختیار داریم. فرض کنید این منبع با محیط اطرافش که در دمای T₀ قرار گرفته، مبادله حرارت دارد. با استفاده از قانون دوم ترمودینامیک بیشترین کار خروجی از فرآیند مذکور را می‌توان با استفاده از رابطه زیر بدست آورد.

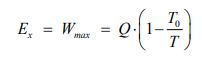
اگر به معادله بالا توجه کنید، می‌بینید که با افزایش دمای منبع، می‌توان کار خروجی بیشتری از سیستم گرفت. بنابراین به نظر می‌رسد که دمای منبع در کیفیت انرژی موجود در آن تاثیر گذار است. شکل زیر همین مفهوم را نشان می‌دهد.

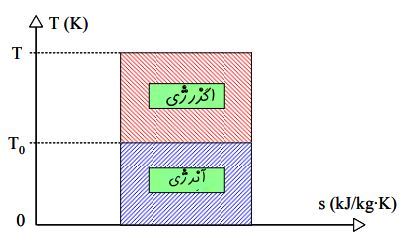
شکل بالا در نمودار T-S نشان داده شده، چرا که میزان انتقال حرارت در یک فرآیند برگشت‌پذیر را می‌توان با استفاده از انتگرال زیر محاسبه کرد.

این نمودار بیان می‌کند که انرژی در حالت کلی به دو بخش تقسیم می‌شود.

۱. بخشی که قابلیت انجام کار را دارد.

۲. بخشی که نمی‌توان از آن کار خروجی دریافت کرد که به آن «آنرژی» (Anergy) گفته می‌شود.

بنابراین برای منبعی با انرژی Q و دمای T که با محیط اطرافش که در دمای T₀ قرار گرفته، مبادله حرارت دارد، می‌توان نوشت:

انرژی = اگزرژی + آنرژی

توجه کنید که گذاره بالا فقط در حالاتی برقرار است که انرژی در قالب حرارت منتقل می‌شود. برای مثال اگر بخشی از انرژیِ سیستم به صورت فشار سیال باشد، گذاره بالا الزاما صحیح نخواهد بود.

بیان‌های اگزرژی

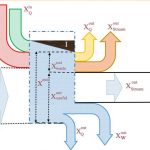
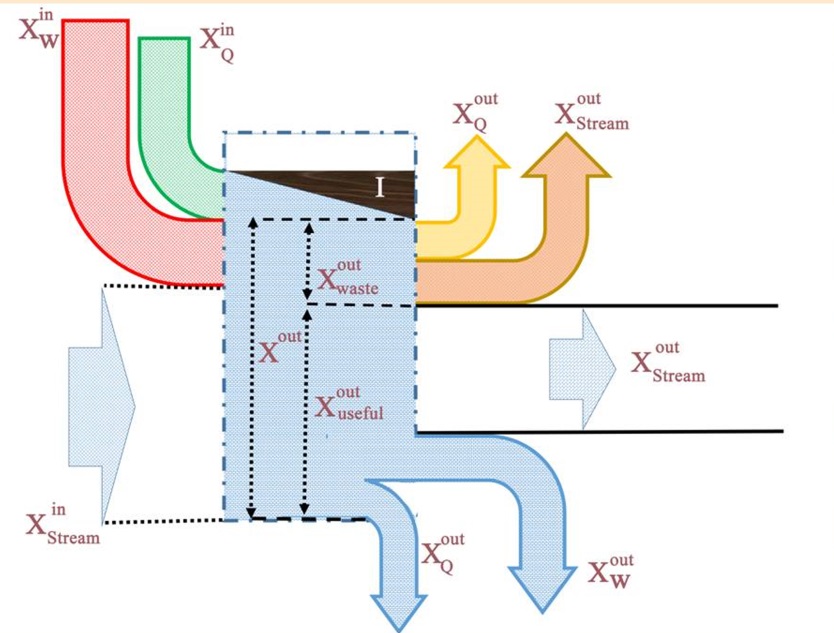
در حالت کلی سیستم فقط شامل انرژی حرارتی نیست و محاسبه اگزرژی به نسبت مشکل‌تر خواهد بود. در ادامه سیستمی را در نظر بگیرید که در آن جریانی با دمای T₁ و P₁ مبادله‌ حرارتی با منبعی با دمای T₀ و P₀ دارد [این مبادله حرارت به صورت برگشت‌پذیر اتفاق می‌افتد]. در حالت ورودی از انرژی جنبشی و پتانسیلِ سیال صرف نظر شده است.

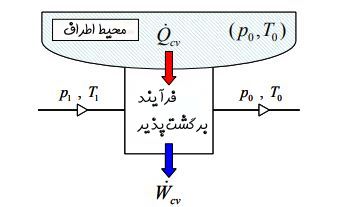
توجه داشته باشید که تمامی تحلیل‌ها با این فرض انجام شده که ماکزیمم انرژی ممکن از سیستم گرفته شود [چرا که فرآیند انتقال حرارت صورت گرفته میان محیط و سیال به صورت برگشت‌پذیر در نظر گرفته شده].

فیلم آموزش ترنسیس – شبیه سازی سیستم های انرژی با TRNSYS 18 – مقدماتی در فرادرس

کلیک کنید

جریان پس از مبادله حرارت با منبع بیرونی به دمای T₀ و P₀ می‌رسد. تمامی انتقال حرارت و کارِ صورت گرفته به صورت پایا است، بنابراین قانون اول ترمودینامیک (بالانس انرژی) را می‌توان به شکل زیر بیان کرد:

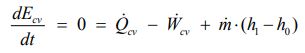
به همین صورت و به دلیل این‌که برگشت‌ناپذیری در این فرآیند فرض نشده، معادله بالانس آنتروپی را می‌توان به شکل زیر نوشت.

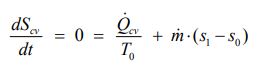
با مرتب کردن معادله بالا به رابطه زیر می‌رسیم. سمت چپ آن، نرخ انتقال حرارت صورت گرفته در واحد جرم است.

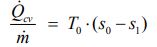
با جایگذاری معادله بالا در رابطه ۱ می‌توان میزان کار منتقل شده در واحد جرم را به شکل محاسبه کرد.

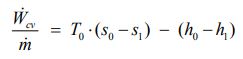
قبلا بیان کردیم که اگزرژی معادل با بیشترین کار منتقل شده‌ی یک سیستم از یک حالت به حالت تعادلش است. این فرآیند دقیقا اتفاقی است که در مثال بالا افتاده. از آنجایی که اگزرژی در قالب بیشترین کار ممکن خروجی از یک سیستم تعریف می‌شود، بنابراین می‌توان به عنوان یک خاصیت ترمودینامیکی به آن نگاه کرد. با توجه به مطالب ارائه شده، رابطه بین خاصیت اگزرژی و کار ایده‌آل انجام شده توسط فرآیند، به شکل زیر است.

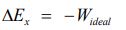
معادله بالا معمولا نسبی است چرا که در آن یک سیستم از یک حالت، در فرآیندی برگشت‌پذیر به حالت دوم می‌رود. اما می‌توان مقداری مطلق نیز برای خاصیت اگزرژی تعریف کرد.

برای سیستمی که فرآیند مرتبط با شکل * را تجربه می‌کند، می‌توان اگزرژی ویژه (اگزرژی بر واحد جرم) را با استفاده از رابطه ۲ و به صورت زیر بدست آورد.

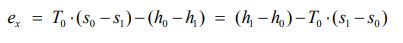
بنابراین تغییرات اگزرژی ویژه برای سیستمی که از حالت ۱ به ۲ می‌رود، به صورت زیر قابل بیان است:

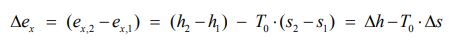
از این رو توجه داشته باشید که فرمت نهایی معادله تغییرات اگزرژی یک سیستم، که از حالت ۱ به ۲ می‌رود به شکل بالا است.

دسته‌ بندی‌های اگزرژی

می‌توان همانند انرژی، اگزرژی را نیز دسته‌بندی کرد. برای نمونه انرژی یک سیال می‌تواند ناشی از فشار، حجم و حرارت موجود در آن باشد. شکل زیر نشان می‌دهد که اگزرژی یک سیستم از چه بخش‌هایی تشکیل شده است.

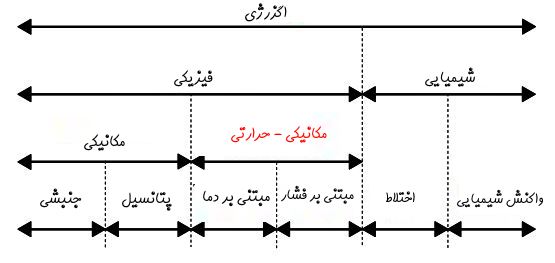
همان‌طور که در شکل بالا نیز نشان داده شده، اگزرژی را می‌توان به دو بخش مبتنی بر فشار و مبتنی بر دما تقسیم‌بندی کرد. این تقسیم‌بندی از نظر فیزیکی تاثیرگذار نخواهد بود و فقط جهت تحلیل راحت‌تر اگزرژی انجام شده است.

فیلم آموزش بهینه سازی جریان اگزرژی Exergy در فرادرس

کلیک کنید

برای نمونه سیستمی را در نظر بگیرید که در دما و فشار T و P قرار گرفته و تحت چندین فرآیندِ برگشت‌پذیر، به دما و فشار T₀ و P₀ می‌رسد. مسیر این فرآیند در شکل زیر نشان داده شده است.

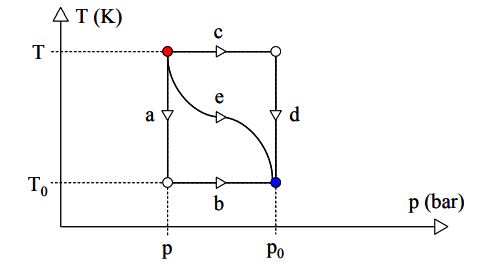
در این شکل سه مسیر برای این فرآیند تعریف شده. این فرآیند می‌تواند با استفاده از مسیر‌های زیر توصیف شود:

1. a+b
2. c+d
3. e

در حقیقت دو فرآیند ۱ و ۲ تقسیم‌ بندی‌های مختلف اگزرژی را نشان می‌دهند. در مسیر c+d در ابتدا دما ثابت و سپس فشار ثابت است؛ در فرآیند a+b برعکس همین داستان اتفاق می‌افتد و برآیند این دو مسیر، e است. فرآیند ۱ و ۲ را به دو بخش دما ثابت و فشار ثابت تقسیم‌بندی می‌کنیم. با این فرض تغییرات اگزرژی را به طور مجزا، برای این دو فرآیند می‌توان به شکل زیر بیان کرد:

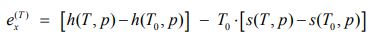
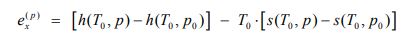
توجه داشته باشید که حرف T، فرآیند دما ثابت و حرف P، مسیر فشار ثابت را نشان می‌دهند.

محاسبه اگزرژی گاز ایده‌آل

همان‌طور که در بخش آنتروپی نیز بیان شد، برای یک گاز ایده‌آل، آنتالپی فقط تابعی از دما و آنتروپی، تابعی از فشار و دما است. دو معادله زیر تغییرات آنتروپی و آنتالپی را برای یک گاز ایده‌آل نشان می‌دهند. نحوه بدست آمدن این دو فرمول در بخش آنتروپی ذکر شده است.

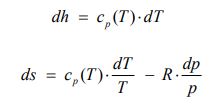
با انتگرال‌گیری از معادلات بالا و با فرض ثابت بودن C_p و R، می‌توان تغییرات آنتالپی و آنتروپی را برای این فرآیند به شکل زیر محاسبه کرد.

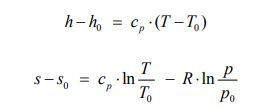
با جایگذاری معادلات بالا در روابط ۳ و ۴ اگزرژی بخش دما ثابت و فشار ثابت به‌ترتیب زیر بدست می‌آیند.

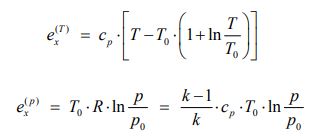
معادلات ۳ و ۴ نشان می‌دهند که اگزرژی مبتنی بر فشار و دما را می‌توان به صورت جدا و با فرض کردن دو فرآیند فشار ثابت و دما ثابت محاسبه کرد. به‌منظور درک بهتر نحوه محاسبه اگزرژی یک سیستم، به مثال زیر توجه فرمایید.

مثال

هوا را به عنوان گاز ایده‌آل فرض کنید که در یک فرآیند، فشارش از  5 بار (bar) به ۱ بار کاهش می‌یابد. فرآیند را آدیاباتیک و برگشت‌پذیر تصور کنید. فرض کنید این فرآیند در دو سناریوی مختلف اتفاق می‌افتد.

۱. دمای اولیه هوا بیشتر از محیط، برابر با ۲۵۰ درجه، معادل با ۵۲۳ کلوین است.

۲. دمای اولیه هوا کمتر از محیط، برابر با ۵۰- درجه، معادل با ۲۲۳ کلوین است.

دما و فشار محیط اطراف را برابر با ۲۵ درجه (۲۹۸ کلوین) فرض کنید. هم‌چنین با توجه به ایده‌آل در نظر گرفتن هوا، روابط زیر  صادق‌اند.

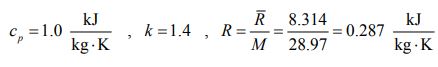
همان‌طور که در بالا نیز بیان شد، میزان کار ایده‌آل انجام شده برابر با تغییر اگزرژی، ولی با علامت منفی است. با استفاده از معادله ۵ و ۶ می‌توان تغییرات اگزرژی را در دو حالت فشار ثابت و دما ثابت، به طور مجزا محاسبه کرد. اندیس a نشان‌دهنده فرض اول (دمای هوا بیشتر از دمای محیط ) و اندیس دوم، فرض دوم (دمای هوا کمتر از دمای محیط) را نشان می‌دهد.

۱. دمای اولیه هوا بیشتر از دمای محیط

اگزرژی مطلق ناشی از فشار و دما در حالت اولیه، برابر است با:

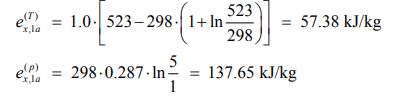
اگزرژی ناشی از دما و فشار در حالت دوم:

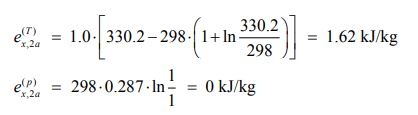
بنابراین بیشترین کار ممکن گرفته شده از این فرآیند برابر با تغییر اگزرژی است که به صورت زیر محاسبه می‌شود.

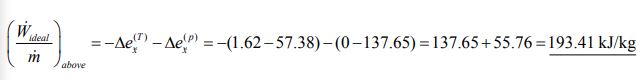
2. دمای اولیه هوا کمتر از دمای محیط

مشابه با حالت ۱ تغییرات اگزرژی را می‌توان به شکل زیر محاسبه کرد.

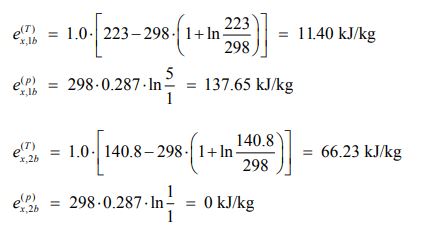
بنابراین بیشترین کار ممکن در حالتی که دمای سیال ورودی کمتر از دمای محیط باشد، برابر است با:

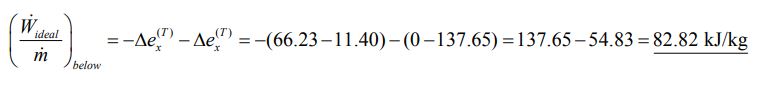
جالب این است که اگر دمای سیال ورودی از دمای محیط بیشتر باشد، با منبسط شدن آن کار بیشتری را می‌توان دریافت کرد.

^^