الگوریتم EM و کاربردهای آن — به زبان ساده

امروزه «مدل‌های مبتنی بر احتمال» (Probabilistic Model) به منظور شناخت ساختار اطلاعات و داده‌ها، در بیشتر علوم، به کار می‌روند. یکی از کاربردهای مهم این مدل‌ها در «یادگیری ماشین» (Machine Learning) و مبحث «خوشه‌بندی برمبنای مدل» (Model Based Clustering) است که طی آن براساس الگوریتم EM، برآورد پارامترهای مدل انجام می‌شود.

از آنجایی که در مدل‌های مبتنی بر احتمال، یک توزیع آماری برای داده‌ها در نظر گرفت می‌شود، می‌توان اهمیت چنین روش‌هایی را استفاده از اطلاعاتی دانست که توزیع آماری داده‌ها به همراه دارند. در چنین حالتی برای برآورد پارامترهای مدل‌های آماری از روش «حداکثر تابع درستنمایی» (Maximum Likelihood Function) استفاده می‌شود. ولی در حالتی که «مقدار گمشده» (Missing Value) یا «داده ناموجود» (Missing Data) در مسئله مطرح باشد امکان برآورد به روش حداکثر درستنمایی به راحتی امکان پذیر نیست. همچنین وجود «متغیر پنهان» (Latent Variable) نیز در این روش، بدست آوردن برآورد مناسب را بسیار سخت می‌کند. بنابراین الگوریتم‌هایی نظیر «الگوریتم EM» $$(Expectation\;\;Maximization)$$ می‌توانند با طی مراحل تکراری، به صورت مناسب پارامترها و در نهایت مدل آماری را برآورد کنند.

 الگوریتم EM

در بسیاری از مسئله‌های برآورد پارامترهای مدل‌ آماری، به شکلی از تابع درستنمایی برخورد می‌کنیم که امکان بیشینه‌سازی آن به روش تحلیلی وجود ندارد. تعداد پارامترهای زیاد، محاسبات تحلیلی را افزایش می‌دهند. در چنین مواقعی با اضافه کردن متغیر پنهان (که البته مقدار آن نیز مشاهده نشده) ممکن است مدل تابع درستنمایی، ساده‌تر شده و امکان محاسبات عددی برای بیشنه‌سازی را فراهم آورد.

فیلم آموزش اوراکل - مدیریت بانک اطلاعاتی با Oracle – تکمیلی در فرادرس

کلیک کنید

الگوریتم EM یکی از روش‌هایی است که براساس وجود متغیر پنهان امکان برآورد پارامترهای مدل آماری را میسر می‌سازد. این الگوریتم اولین بار توسط «آرتور دمپستر» (Arthur Dempster) دانشمند آمار و همکارانش در مقاله‌ای با عنوان «حداکثر درستنمایی برای داده‌های ناکامل برمبنای الگوریتم EM» ($$Maximum\;Likelihood\;from\;Incomplete\;Data\;via\;the\;EM\;Algorithm$$)  که در سال 1977 منتشر شد معرفی گردید؛ آنها نشان دادند که الگوریتم EM می‌تواند ابزاری موثر در تحلیل‌های آماری بخصوص برآورد به روش حداکثر تابع درستنمایی باشد.

در این الگوریتم پارامترها را به دو گروه تفکیک می‌کنیم. در مرحله اول برای پارامترهای گروه اول مقدارهایی به عنوان «مقادیر اولیه» (Initial Values) در نظر گرفته و براساس این پارامترها، مقدار پارامترهای گروه دوم را برآورد می‌کنیم. حال براساس پارامترهای گروه دوم و داده‌های مشاهده شده پارامترهای گروه اول را برآورد کرده و آن‌ها را بهبود می‌دهیم. این کار تا زمانی که الگوریتم به همگرایی برسد تکرار می‌شود. نتیجه نهایی از برآورد پارامترهای مدل در الگوریتم EM، تابع درستنمایی را به حداکثر مقدار خود می‌رساند.

در ادامه برای روشن شدن این مراحل، به یک مثال معروف در این زمینه می‌پردازیم.

مثال

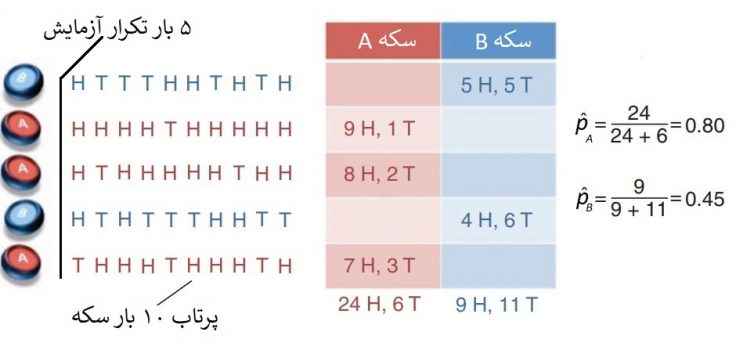
فرض کنید دو سکه A و B در اختیار داریم که احتمال شیر آمدن برای سکه A برابر با $$p_A$$ و برای سکه B نیز این احتمال برابر با $$p_B$$‌ است. هدف برآورد این احتمالات $$(p_A,p_B)$$‌ است. یک آزمایش به صورت زیر ترتیب می‌دهیم و آن را ۵ بار تکرار می‌کنیم. یک سکه را به تصادف انتخاب می‌کنیم و آن را ده بار پرتاب می‌کنیم و X را متغیر تصادفی تعداد شیرها در نظر می‌گیریم. اگر بدانیم ۳ بار سکه A‌ انتخاب شده است، مشخص است که $$X\sim B(30,p_A)$$.

فیلم آموزش طراحی واکنش گرا با گرید و فلکس باکس Grid و Flexbox در CSS در فرادرس

کلیک کنید

مقدارهای مشاهده شده برای این آزمایش شامل ۵۰ بار پرتاب سکه‌ها است. نتایج را در تصویر ۱ می‌توان مشاهده کرد. همانطور که مشخص است احتمال اینکه شیر از سکه A‌ مشاهده شود برابر با 0.80 و احتمال مشاهده شیر در سکه B برابر با 0.45 است. این مقدارها، برآورد براساس تابع درستنمایی هستند. زیرا لگاریتم تابع درستنمایی برای سکه A به صورت زیر است که با گرفتن مشتق، مشخص می‌شود که تابع درستنمایی دارای مقدار حداکثر در نقطه $$p=\dfrac{\sum_{i=1}^{30} x_i}{30}$$ خواهد بود.

$$l(p_A)=\sum_{i=1}^{30} x_i ln(p_A)+(30-\sum_{i=1}^{30}x_i)ln(1-p_A)$$

 به همین شکل نیز می‌توان تابع درستننمایی را برای پارامتر $$p_B$$ نوشت و محاسبات مربوطه را انجام داد.

ولی این بار حالتی را در نظر بگیرید که در هر بار تکرار آزمایش یک سکه را انتخاب می‌کنیم و نمی‌دانیم که سکه A‌ انتخاب شده یا سکه B. حال به چه ترتیب باید تابع درستنمایی و برآورد پارامترها را انجام داد. فرض کنید در این حالت متغیر تصادفی Z (متغیر پنهان) یک متغیر برنولی است که مقدار ۱ و ۰ را می‌گیرد. اگر سکه A‌ انتخاب شده باشد Z=1 و اگر سکه B انتخاب شده باشد Z=0 خواهد بود. به این ترتیب با استفاده از الگوریتم EM سعی در برآورد پارامترهای $$p_A$$ و $$p_B$$ داریم.

مراحل الگوریتم EM برای این مسئله در تصویر ۲ دیده می‌شود. برای بررسی چگونگی عملکرد الگوریتم EM، هر یک از مراحل را مرور می‌کنیم.

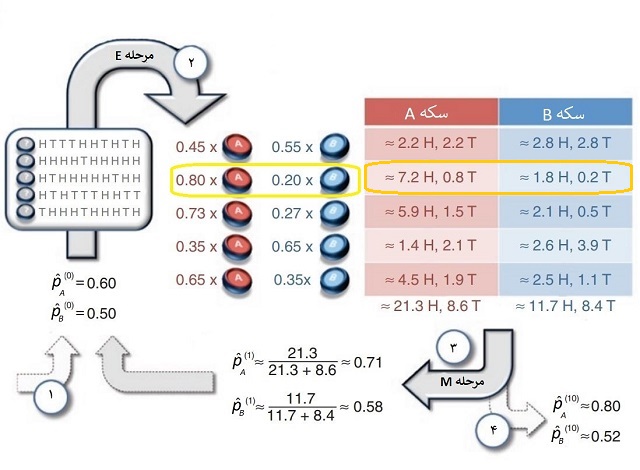
1. حدس اولیه برای پارامترها $$(p_A=0.60)$$‌ و $$(p_B=0.50)$$. انجام آزمایش تصادفی و ثبت نتایج متغیرهای تصادفی X.
2. محاسبه امیدریاضی (متوسط گیری) برای تعداد شیرها و خط‌های هر کدام از سکه‌های A و B (ستون‌های جدول).
3. حداکثرسازی تابع درستنمایی مربوطه با توجه به متغیر تصادفی Z. برآورد پارامترها.
4. استفاده از پارامترهای بدست آمده در مرحله قبل به عنوان ورودی‌های جدید الگوریتم. تکرار مراحل الگوریتم، تا رسیدن به همگرایی در جواب‌های نهایی.

دقت کنید که برای برآورد پارامترها در مرحله E باید از احتمال شرطی و قضیه بیز کمک گرفت. از طرفی می‌دانیم که متغیر تصادفی مربوط به تعداد شیرهای مشاهده شده در پرتاب سکه دارای توزیع دو جمله‌ای است. برای درک بهتر از شیوه محاسبه مقدارها در این مرحله، عملیاتی که در سطر دوم (کادر زرد و نارنجی) انجام شده را بررسی می‌کنیم.

فرض کنید پیشامد انتخاب سکه A (در نتیجه $$p_A=0.6$$) را با Z=1 و پیشامد انتخاب سکه B (در نتیجه $$p_B=0.4$$) را با Z=0 نشان دهیم. مقدار احتمال برای هر یک از این دو پیشامد را نیز برابر در نظر می‌گیریم،  زیرا هر سکه بطور تصادف انتخاب می‌شود، یعنی $$P(Z=1)=P(Z=0)=\tfrac{1}{2}$$. همچنین پیشامد مشاهده یک خط و ۹ شیر را با علامت $$H9T1$$  نشان می‌دهیم.

$$P(z=1|H9T1)=\dfrac{P(H9T1|z=1)P(z=1)}{P(H9T1|z=1)P(z=1)+P(H9T1|z=0)P(z=0)}=$$

$$\dfrac{{10 \choose 9} \times (0.6)^9 \times (0.4)^1 \times\tfrac{1}{2}}{{10 \choose 9} \times (0.6)^9 \times (0.4)^1 \times \tfrac{1}{2}+ {10 \choose 9} \times (0.5)^9 \times (0.5)^1 \times \tfrac{1}{2}}$$

و به همین ترتیب باید عملیات را برای $$P(Z=0|H9T1)$$ انجام دهیم. در نهایت نتایج زیر بدست می‌آید:

$$P(Z=1|H9T1)=0.80, \;\;\;\;P(Z=0|H9T1)=0.20$$

براساس این احتمالات باید امید-ریاضی شرطی نیز محاسبه شود. از آنجایی که احتمال مشاهده ۹ بار شیر از سکه A برابر با 0.8 است، می‌توان امید-ریاضی را به صورت $$E_{z=1}(X|H9T1)=0.8 \times 9=7.2$$ نوشت. مشخص است که متوسط تعداد خط‌ها برای سکه A نیز برابر خواهد بود با $$0.8 \times 1 =0.8$$. به همین ترتیب برای سکه B نیز می‌توان انتظار داشت که متوسط تعداد شیرها برابر با $$0.20 \times 9=1.8$$ و متوسط تعداد خط‌ها برابر با $$0.2 \times 1=0.2$$ باشد.

در مرحله ۳ نیز نسبت تعداد کل شیرها به تعداد کل پرتاب‌ها برای سکه A برآورد حداکثر درستنمایی پارامتر $$p_A$$ خواهد بود. این مقدار در تکرار اول الگوریتم برابر با 0.71 است. همین گونه برآورد را نیز برای $$p_B$$ انجام می‌دهیم و به مقدار 0.58 می‌رسیم. این برآوردها برای پارامترها، به عنوان ورودی‌های جدید در الگوریتم وارد شده و محاسبات تکرار می‌شوند. در تصویر ۲، تعداد تکرارها ۱۰ بار در نظر گرفته شده است، در نتیجه آخرین برآورد با $$\hat{p_A}^{(10)}$$ نشان داده شده است.

پس با استفاده از این مشاهدات و الگوریتم EM در این مثال به این نتیجه رسیدیم که احتمال مشاهده شیر برای سکه A برابر با 0.80 و برای سکه B نیز برابر با 0.52 خواهد بود. همچنین با استفاده از قسمت میانی تصویر ۲ می‌توان مشخص کرد که مشاهدات از ۱۰ بار پرتاب متعلق به کدام سکه بوده است. برای مثال از آنجایی که در سطر دوم برای سکه A احتمال برابر با 0.8 شده است، مشخص می‌شود که مشاهدات HHHHTHHHHH مربوط به سکه A بوده و یا در سطر چهارم با توجه به اینکه برای سکه B احتمال برابر با 0.65 است، مشخص می‌شود که مشاهدات HTHTTTHHTT مربوط به سکه B‌ بوده.

اگر مطلب بالا برای‌تان مفید بوده است، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش‌های نرم‌افزارهای آماری
• احتمال شرطی (Conditional Probability) --- اصول و شیوه محاسبه
• قضیه بیز در احتمال شرطی و کاربردهای آن
• آموزش آمار و احتمال مهندسی
• آزمایش تصادفی، پیشامد و تابع احتمال
• متغیر تصادفی و توزیع دو جمله‌ای — به زبان ساده

^^