پتانسیل الکتریکی (Electric Potential) – از صفر تا صد (+ دانلود فیلم آموزش گام به گام)
در دو بخش میدان الکتریکی و قانون کولن در مورد اصول الکتریسیته صحبت شد. در این قسمت قصد داریم تا در مورد بخش مهمی از الکتریسیته تحت عنوان پتانسیل الکتریکی بحث کنیم. بدین منظور در ابتدا مفهوم عمومی پتانسیل را تشریح میکنیم.

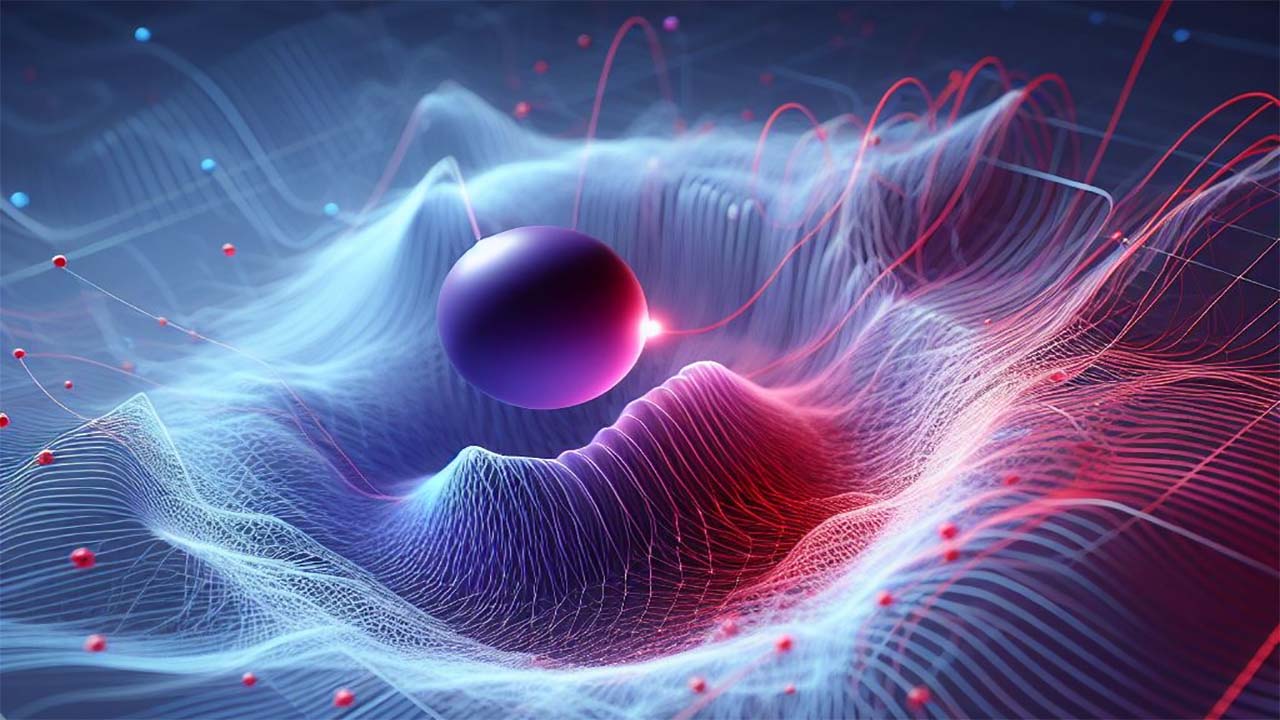
مفهوم انرژی پتانسیل
از مباحث پایهای فیزیک میدانید که هرگاه دو جرم در فاصلهای از یکدیگر قرار گیرند، نیرویی به هم وارد میکنند که با مجذور فاصله آنها رابطهای عکس دارد. با استفاده از این مفهوم میتوان گفت که زمین نیز نیرویی به هر جرم وارد میکند که ما آن را تحت عنوان «وزن» میشناسیم. نیروی وارد شده به جرم m برابر است با:
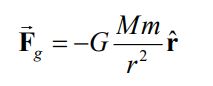
در رابطه بالا ، ثابت گرانشی است و بردار واحدی است که راستای آن بین زمین و جرم مفروض است. جرم زمین به صورت یکنواخت و برابر با M در نظر گرفته میشود. با ثابت بودن M و G واضح است که با تقسیم نیروی بدست آمده از رابطه بالا به جرم m، شتاب ثابتی بدست میآید. این شتاب را با نشان میدهند. در نتیجه برابر است با:
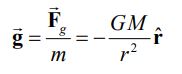
حال مطابق با شکل زیر فرض کنید جرم m تحت تاثیر نیروی گرانش زمین، از نقطه A تا نقطه B جابجا میشود.
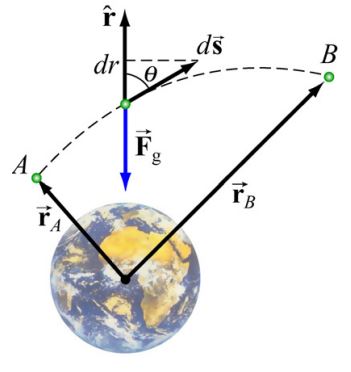
با این فرضیات، کار انجام شده توسط گرانش در فاصله A تا B برابر است با:
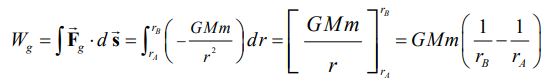
همانطور که از رابطه بالا نیز میتوان برداشت کرد، میزان کار انجام شده توسط گرانش تنها به موقعیت اولیه و نهایی جرم m وابسته است. در حقیقت مقدار کار انجام شده مستقل از مسیر جابجایی جرم m است. توجه داشته باشید که کار انجام شده توسط نیروی گرانشی (WG) و نیروی وارد شده از طرف شما (Wext) با یکدیگر متفاوت است. به سادگی میتوان نشان داد کار انجام شده توسط این دو نیرو عکس هم هستند (WG= -Wext).
مطابق با شکل زیر تصور کنید که نیروی وزن، جرم m را از ارتفاع A به B جابجا میکند.
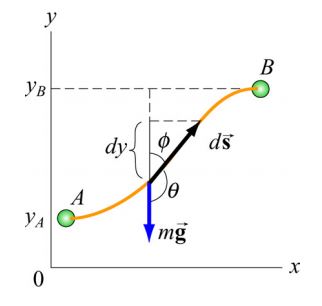
در نزدیکی سطح زمین، میدان گرانشی تقریبا ثابت و برابر با در نظر گرفته میشود. با ثابت فرض کردن g در نزدیکی زمین، میتوان گفت کار انجام شده توسط نیروی گرانشی، هنگامی که جرم m از yA به yB جابجا میشود، برابر است با:
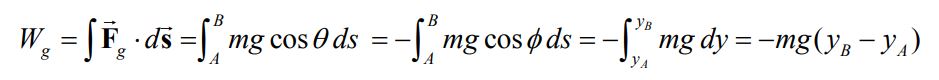
همانطور که در رابطه بالا میبینید در این حالت نیز کار انجام شده، مستقل از مسیر فرآیند است. با این فرض اگر جرم m مسیر بستهای را طی کند، کار خالص انجام شده توسط گرانش روی مسیر مفروض، صفر بدست میآید؛ به این دلیل به نیروی گرانش، نیروی پایا گفته میشود. از این رو به هر نیرویی که در رابطه پایین صدق کند، نیروی پایسته گفته میشود.
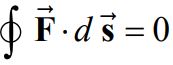
در حقیقت رابطه بالا کار انجام شده توسط نیروی F را روی یک مسیر بسته نشان میدهد. در حالاتی که با نیروهای پایسته سروکار داریم، مناسب آن است که مفهومی تحت عنوان پتانسیل را تعریف کنیم. این کمیت را با نماد U نشان میدهند و برابر با منفی مقدار کاری است که توسط نیروی F روی جرم m انجام میشود. از این رو میتوان تغییرات پتانسیل یک سیستم را با استفاده از رابطه زیر توصیف کرد.
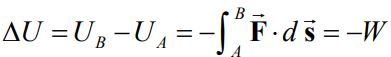
در حقیقت رابطه بالا میگوید: انرژی پتانسیلی که در سیستم ذخیره شده، عکس کاری است که نیروی W در مسیر، روی جرم انجام داده است. در حالتی که گرانش روی جرم کار انجام دهد، رابطه بالا را میتوان به شکل زیر نوشت:
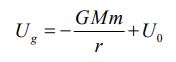
در رابطه بالا U0 مقداری مشخص است که به انتخاب نقطه مرجع وابسته است. مرسوم است که نقطه مرجع را به شکلی انتخاب میکنند تا انرژی پتانسیل مربوط به آن صفر شود. در مسئله گرانش معمولا نقطه بیهنایت به عنوان نقطه مرجع در نظر گرفته میشود. در نتیجه انرژی مرتبط با آن (U0) برابر با صفر فرض میشود. از آنجایی که مقدار مطلق پتانسیل به نقطه مرجع انتخاب شده وابسته است، بنابراین تنها تغییرات پتانسیل مهم تلقی میشوند. با این فرضیات در حالتی که جرم m از سطح زمین تا ارتفاع h جابجا شود، تغییرات انرژی پتانسیل آن برابر است با:
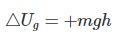
انرژی پتانسیل و روابط آن در دو مطلب انرژی پتانسیل و قضیه کار و انرژی به خوبی مورد مطالعه قرار گرفته است. مفهوم مهم دیگری که از انرژی پتانسیل استخراج میشود، «پتانسیل» (Potential) است. این مقدار نشان دهنده منفی میزان کاری است که به ازای بار الکتریکی جرم واحد انجام میشود. تعریف ریاضیاتی پتانسیل به صورت زیر است.
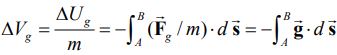
Vg∆ منفی کاری است که گرانش برای جابجایی جرم واحد از نقطه A به B انجام میدهد. بهمنظور بیان مفهوم انرژی پتانسیل و پتانسیل الکتریکی دقیقا از همین مفهوم استفاده میکنیم. با فرض پایسته بودن نیروی کولن، انرژی پتانسیل بر واحد بار الکتریکی برای یک میدان الکتریکی را میتوان به صورت زیر تعریف کرد [در این حالت بار الکتریکی معادل جرم و نیروی کولن معادل با نیروی گرانش است].
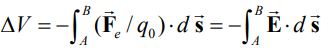
در رابطه بالا q0 بار آزمون است که از آن در بیان مفهوم میدان الکتریکی نیز بهره بردیم. با توجه به رابطه بالا، اختلاف پتانسیل را میتوان با استفاده از عبارت زیر تعریف کرد:
به میزان کاری که میدان الکتریکی E در واحد بار، برای جابجایی بار آزمون q0 از نقطه A به B انجام میدهد، اختلاف پتانسیل (V∆) گفته میشود.
توجه داشته باشید که جابجایی انجام شده در بالا بایستی بدون تغییر انرژی جنبشی اتفاق بیافتد. دوباره تاکید میکنیم که انرژی پتانسیل و پتانسیل الکتریکی با یکدیگر متفاوت هستند و نبایستی آنها را با یکدیگر اشتباه گرفت. این دو کمیت فیزیکی را میتوان با استفاده از رابطه زیر به هم مرتبط کرد.
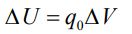
از رابطه بالا میتوان فهمید که واحد پتانسیل الکتریکی (V) - که به آن ولتاژ نیز گفته میشود - در سیستم SI عبارت است از:
1 V = 1 کولن/ژول
در حالتی که با سیستمی در مقیاس اتمی یا مولکولی مواجه هستیم، ۱ ژول انرژی بالایی برای توصیف سیستم محسوب میشود. از این رو در این مقیاس از عددی تحت عنوان الکترون-ولت (eV) استفاده میشود. این مقدار نشاندهنده میزان انرژی است که یک الکترون از حرکت در اختلاف پتانسیل ۱ ولت بدست میآورد و یا از دست میدهد. بنابراین مقدار ۱ الکترون-ولت برابر است با:
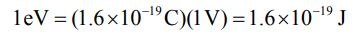
پتانسیل الکتریکی در یک میدان یکنواخت
باری به اندازه q+ را در نظر بگیرید که در میدانی مطابق با شکل زیر حرکت میکند.

از آنجایی که مسیر حرکت بار و میدان در یک راستا هستند، بنابراین اختلاف پتانسیل در فاصله A تا B برابر با مقدار زیر محاسبه میشود.
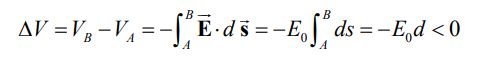
رابطه بالا نشان میدهد که پتانسیل نقطه B از نقطه A کمتر است. در حقیقت خطوط میدان الکتریکی همواره ذرات باردار را از پتانسیل بالاتر به پتانسیل پایینتر منتقل میکنند. با ضرب کردن مقدار اختلاف پتانسیل در بار ذره، اختلاف انرژی پتانسیل بین دو نقطه جابجا شده بدست میآید. در نتیجه اختلاف انرژی پتانسیل بین دو نقطه A و B برابر است با:
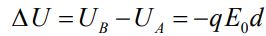
پیشنهاد میکنیم که به صورت مجزا در مورد مفهوم فیزیکی رابطه بالا در دو حالتی که بار ذره مثبت و منفی باشند، فکر کنید. جالب است بدانید که در هر دو حالت اختلاف انرژی پتانسیل بدست آمده، منفی خواهد بود. رابطه بالا مربوط به زمانی است که مسیر حرکت ذره و میدان همجهت باشند.
حال تصور کنید یک بار الکتریکی مسیری را مطابق با شکل پایین طی کند. به نظر شما اختلاف پتانسیل بار در این حالت به چه شکل تغییر میکند؟
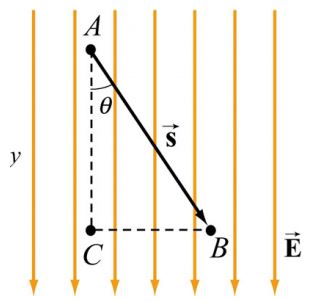
همانگونه که در شکل بالا نیز مشخص شده در این حالت زاویه بین مسیر حرکت بار و میدان برابر با θ است. این زاویه در حاصلضرب داخلی که در زیر انتگرال قرار گرفته، ظاهر خواهد شد. نهایتا اختلاف پتانسیل در این حالت برابر است با:
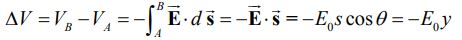
در محاسبه انتگرال بالا توجه کنید که جهت مثبت محور y به سمت پایین در نظر گرفته شده. رابطه بالا نیز کاهش پتانسیل الکتریکی در نتیجه حرکت ذره باردار را نشان میدهد.
حال تصور کنید همین بار و در همین میدان، مسیر را طی کند. در این جابجایی تغییرات پتانسیل شامل دو قسمت میشود که در ادامه بیان شده.
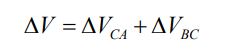
در بخش اول مسیر که ذره از A به سمت C حرکت میکند، پتانسیل بار به اندازه تغییر میکند. در مسیر C به B با توجه به اینکه بردار جابجایی و بردار میدان الکتریکی به یکدیگر عمود هستند، بنابراین حاصلضرب داخلی این دو نیز صفر است و یا به شکلی بهتر میتوان گفت که پتانسیل نقاط C و B با یکدیگر برابر هستند. صفر بودن اختلاف پتانسیل بین این دو نقطه نشان میدهد که بهمنظور جابجایی بار بین دو نقطه مفروض نیاز نیست کاری انجام شود. همچنین تمامی مسیرهای بین B و C، اختلاف پتانسیلشان صفر هستند.
پتانسیل الکتریکی ناشی از بارهای نقطهای
بدیهی است که هر بار الکتریکی، پتانسیلی را در اطراف خود ایجاد خواهد کرد. در حقیقت میدان بوجود آمده توسط بارهای الکتریکی منجر به ایجاد اختلاف پتانسیل میشوند. بهمنظور بررسی پتانسیل و میدان الکتریکی اطراف بار، شکل زیر را در نظر بگیرید.
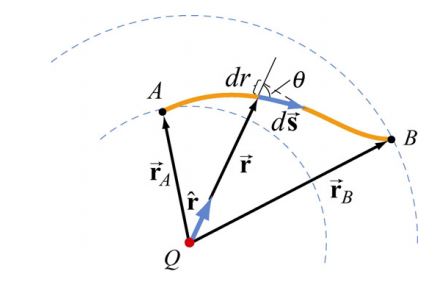
همانطور که در بخش میدان الکتریکی تشریح شد، بار نشان داده شده در شکل بالا میدانی را در فاصله r از خود ایجاد میکند که با استفاده از فرمول زیر بدست میآید.
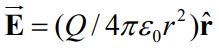
در رابطه بالا نشان دهنده بردار واحدی است که جهت میدان الکتریکی را نشان میدهد. اختلاف پتانسیل بین دو نقطه A و B را میتوان با استفاده از تعریف و به شکل زیر محاسبه کرد.
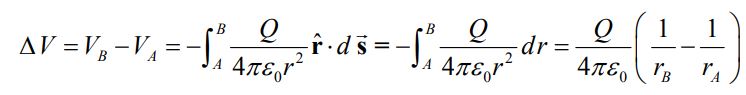
عبارت بالا شبیه به کدام رابطه در فیزیک است؟ بله درست حدس زدید، چراکه این عبارت همانند رابطه اختلاف پتانسیل در میدان گرانشی است. نکته مهم در رابطه بالا این است که دوباره مشاهده شد که اختلاف پتانسیل بین دو نقطه تنها به موقعیتهای آنها وابسته است و مستقل از مسیر طی شده میان A و B است. همانند گرانش، با فرض اینکه پتانسیل الکتریکی در بینهایت برابر با صفر باشد، پتانسیل الکتریکی در نقطه مشخص P را میتوان به شکل زیر محاسبه کرد.
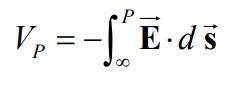
با محاسبه انتگرال بالا، پتانسیل الکتریکی در فاصله r از یک ذره، مطابق با رابطه زیر محاسبه میشود.
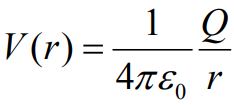
زمانی که هدف ما محاسبه پتانسیل الکتریکی حاصل از چندین ذره باشد، میتوان با جمع زدن پتانسیل حاصل از هر ذره به این مقدار دست یافت. در حقیقت قانون جمع آثار در این مسئله نیز برقرار است. در جدول زیر روابط معادل در محاسبات مربوط به گرانش و الکتریسیته بیان شده.
انرژی پتانسیل مجموعهای از بارهای الکتریکی
فرض کنید تعدادی بار الکتریکی داریم و آنها را از بینهایت جابجا کرده و به شکل خاصی ا کنار هم نگه میداریم. واضح است که بایستی با انجام کار خارجی این عمل را انجام دهیم. نهایتا کار انجام شده به صورت انرژی پتانسیل در سیستم ذخیره میشود. در حقیقت رابطه U=+Wext∆ را میتوان نوشت. برای درک بهتر، فرض کنید که میخواهید جرم m را از زمین بلند کرده و در ارتفاع h قرار دهید. واضح است که بایستی نیرویی به اندازه وزن و در خلاف جهت حرکت به جرم وارد شود. از آنجایی که نیروی وارد شده و مسیر حرکت جرم در یک جهت هستند، کار انجام شده در این فرآیند برابر با F×h=W×h=mgh است. همانطور که از قبل نیز میدانید انرژی پتانسیل جرم m در ارتفاع h (نسبت به سطح زمین) برابر با mgh بدست آمده است.
برای بررسی انرژی پتانسیل سیستمی از ذرات، در ابتدا مطابق با شکل زیر دو بار q1 و q2 را در نظر بگیرید.
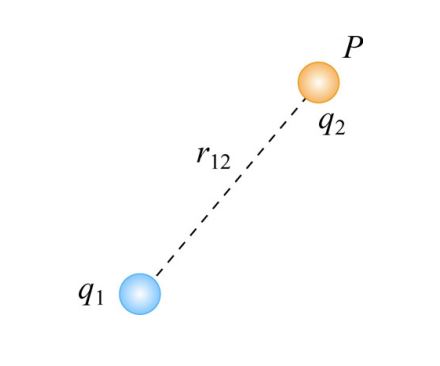
همانطور که میبینید فاصله این ذرات را با r12 نشان دادهایم. فرض کنید که ذره ۱ ساکن است و ذره ۲ از بینهایت به آن نزدیک شده. با این فرض کار انجام شده روی بار q2 برابر با تغییر پتانسیل آن است. تغییر پتانسیل بار q2 هنگامی که آن را از بینهایت جابجا کرده و در فاصل r12 از بار q1 قرار میدهیم، برابر است با:
ΔU2=q2V1
V1 پتانسیلی است که ذره ۱ اطراف خود ایجاد میکند. در حقیقت تغییر انرژی بدست آمده برای ذره ۲ همان کاری است که برای جابجایی آن بایستی انجام شود. نهایتا کار انجام شده روی ذره ۲ در این جابجایی را میتوان به صورت زیر بیان کرد:
رابطه ۱ W2=ΔU2=q2V1
همانطور که قبلا بیان شد، پتانسیل V1 برابر است با:
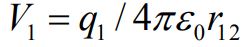
با جایگذاری مقدار بالا در رابطه ۱ مقدار کار لازم و نتیجتا انرژی مجموعه دو بار که در فاصله r12 از یکدیگر قرار گرفتهاند، برابر با مقدار زیر بدست میآید.
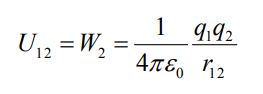
اگر علامت دوبار مشابه باشد (هردو مثبت یا هردو منفی)، به منظور نگه داشتن دو بار کنار یکدیگر بایستی کار انجام شده مثبت و درنتیجه U12>0 و در حالتی که علامت بارها مخالف هم باشد، U12<0 است. این استدلال را میتوان برای سیستمهای با تعداد بالاتری از ذره نیز تعمیم داد. برای نمونه اگر در همین مسئله بخواهیم بار q3 را نیز اضافه کنیم، کار مورد نیاز برابر است با:
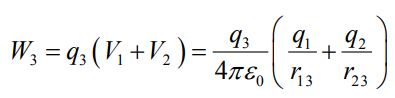
شکل زیر شماتیک سیستمی سهذرهای را نشان میدهد.
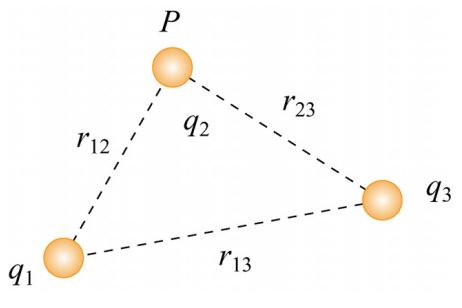
نهایتا پتانسیل الکتریکی را میتوان با استفاده از جمع زدن کارهای انجام شده، به شکل زیر بدست آورد.
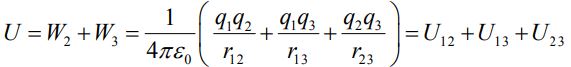
رابطه بالا نشان میدهد که برای یک سیستم چند ذرهای بایستی کار مورد نیاز برای قرار دادن دو به دو ذرات کنار هم را با یکدیگر جمع زد. معادل ریاضی این عبارت، رابطه زیر است.
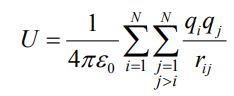
شرط j>i برای جلوگیری از جمع زدن دوباره یک عبارات قرار داده شده است.
پتانسیل حاصل از توزیع پیوستهای از بارهای الکتریکی
همانند محاسبه میدان الکتریکی در حالتی که با تودهای از بار مواجهایم، میتوان با استفاده از انتگرالگیری از جزء بار مورد بررسی، پتانسیل کل سیستم را بدست آورد. مطابق شکل زیر تودهای از بار الکتریکی را فرض کنید.
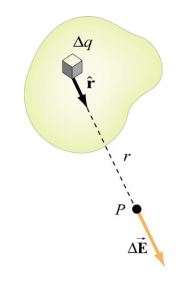
با فرض اینکه نقطه مرجع در بینهایت باشد، پتانسیل ناشی از جزء بار را میتوان با استفاده از رابطه زیر محاسبه کرد.
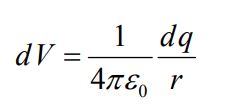
با انتگرالگیری از رابطه بالا پتانسیل کل توده به شکل زیر محاسبه میشود.
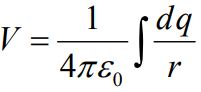
مفهوم چگالی بار به طور مفصل در اینجا توضیح داده شده لذا در صورتی که احساس میکنید به توضیح بیشتری نیازمند هستید، میتوانید به آن مراجعه کنید.
مثال ۱
مطابق شکل زیر میلهای را به طول l در نظر بگیرید که چگالی بار روی آن برابر با λ است.

پتانسیل الکتریکی در نقطه P که در فاصله عمودی y از میله قرار دارد را بیابید.
برای حل این مسئله در ابتدا طول دیفرانسیلی برابر با 'dx را فرض کنید که بار 'dq=λdx روی آن قرار گرفته است. بنابراین در قدم اول قصد داریم تا پتانسیل ناشی از بار جزئی قرار گرفته در مختصات (x',0) را محاسبه کنیم. از فیثاغورث میدانیم که فاصله 'dx تا P برابر با است. با توجه به دیفرانسیل فرض شده، پتانسیل جزئی ناشی از بار کوچک در نظر گرفته شده برابر است با:
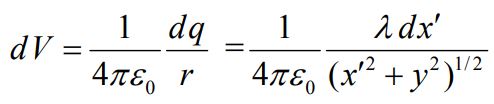
با فرض اینکه پتانسیل V در بینهایت برابر با صفر باشد، مقدار پتانسیل در فاصله مشخص شده در شکل را میتوان با انتگرالگیری از رابطه بالا و به صورت زیر محاسبه کرد.
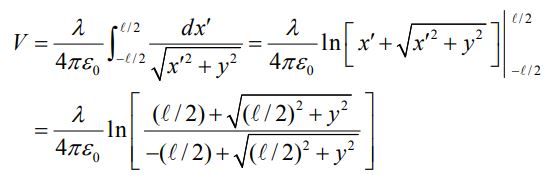
در محاسبه انجام شده در بالا از رابطه زیر بهمنظور محاسبه انتگرال استفاده شده است.
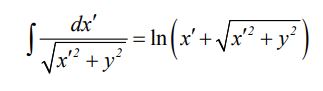
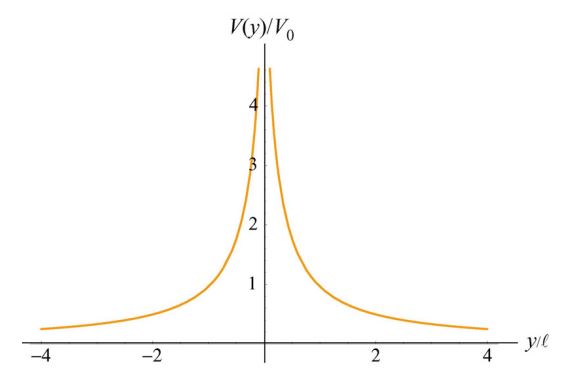
در نمودار زیر مقدار V(y)/V0 بر حسب فاصله y نشان داده شده که در آن است.
مثال ۲
حلقهای به شعاع R را در نظر بگیرید که دارای چگالی بار λ است. در شکل زیر این حلقه نشان داده شده است. برای چنین سیستمی پتانسیل الکتریکی در فاصله z از مرکز حلقه چقدر است؟
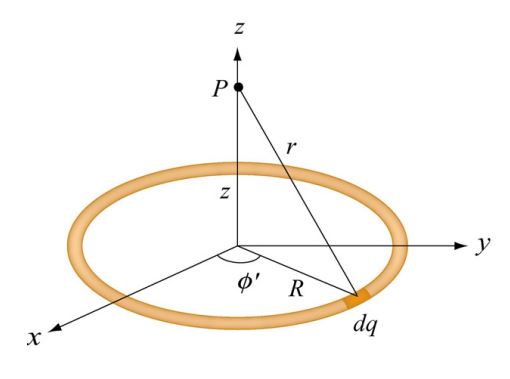
همانند مسئله قبل در این مثال نیز در ابتدا جزئی دیفرانسیلی را به طول 'dl=Rdφ در نظر میگیریم. از این رو مقدار بار موجود در این جزء از حلقه برابر با 'dq=λdl=λRdφ است. در نتیجه پتانسیل ناشی از آن را میتوان با استفاده از رابطه زیر بدست آورد.
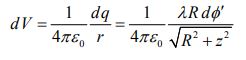
نهایتا با انتگرالگیری از رابطه بالا پتانسیل الکتریکی کل حلقه برابر با مقدار زیر محاسبه میشود.
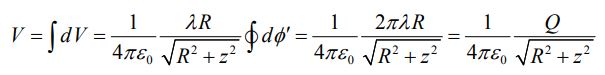
جالب است بدانید که در حالت حدی که فاصله z را بسیار بزرگتر از R انتخاب میکنیم، رابطه مربوط به پتانسیل نقطهای بدست میآید. معنای ریاضیاتی این جمله را میتوان به شکل زیر بیان کرد:
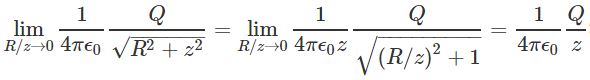
نکته مهمی که در اینجا میتوان به آن اشاره کرد، این است که با حل کردن مثالهای بسیار در زمینه پتانسیل الکتریکی میتوانید حتی به مفاهیم پایهای مرتبط به آن نیز مسلط شوید. البته در اینجا مفاهیم، اصول و همچنین مثالهای بسیاری در زمینه پتانسیل الکتریکی و در قالب ویدئو ارائه شده که میتواند به درک هرچه بهتر شما از این مطلب کمک کند.
ارتباط بین میدان و پتانسیل الکتریکی
قبلا رابطهای را به صورت زیر معرفی کردیم که با استفاده از آن قادر بودیم تا پتانسیل الکتریکی را با استفاده از میدان محاسبه کنیم.
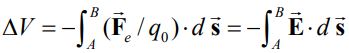
اما این سوال مطرح میشود که آیا میتوان با داشتن پتانسیل الکتریکی میدان را بدست آورد؟ برای پاسخ به این سوال در ابتدا دو نقطه را در نظر بگیرید که در فاصله دیفرانسیلی از یکدیگر قرار گرفتهاند. میدانیم که اختلاف پتانسیل بین دو نقطه مفروض را میتوان به شکل دیفرانسیلی زیر بیان کرد:
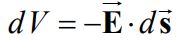
بهمنظور محاسبه ضرب داخلی، بردار فاصله میان این دو نقطه و میدان را میتوان در مختصات کارتزینی به شکل زیر بیان کرد.
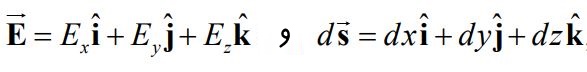
در نتیجه حاصلضرب داخلی دو بردار میدان و جابجایی برابر است با:
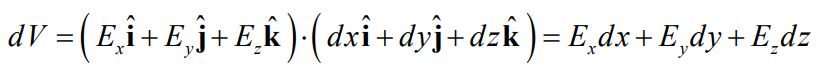
از طرفی با توجه به اینکه V یک اسکالر است، میتوان تغییرات جزئی آن را با استفاده از مشتقگیری پارهای و به شکل زیر توصیف کرد.
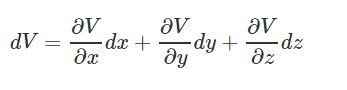
با برابر قرار دادن سمت راست دو معادله بالا با یکدیگر به عبارت زیر میرسیم.
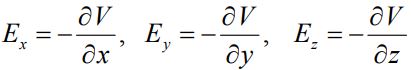
رابطه بالا نشان میدهد که با مشتقگیری پارهای از پتانسیل در یک جهت خاص، میدان الکتریکی در همان جهت بدست میآید. بنابراین نهایتا توانستیم رابطهای مطرح کنیم که با استفاده از آن قادریم تا با داشتن پتانسیل، میدان الکتریکی را محاسبه کنیم. سوالی که باقی میماند این است که میدان یک کمیت برداری و پتانسیل کمیتی اسکالر - یا نردهای - است. چطور میتوان در قالب یک رابطه این دو کمیت را به یکدیگر مرتبط کرد؟
برای پاسخ به این سوال بایستی با عملگری ریاضیاتی تحت عنوان «گرادیان» آشنا باشید. این عملگر را با علامت نشان میدهند. در حقیقت عملگر مذکور با عمل کردن روی یک اسکالر آن را به بردار تبدیل میکند. عملگر گرادیان را میتوان به صورت زیر تعریف کرد:
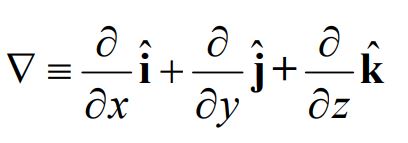
با استفاده از عملگر تعریف شده، میدان الکتریکی را میتوان به صورت حاصلضرب برداری آن در اختلاف پتانسیل دانست. در نتیجه میتوان گفت:
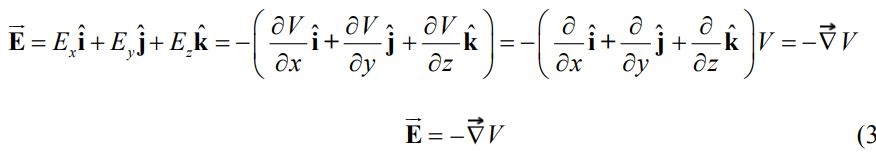
سادهترین بیان مرتبط با عبارت بالا این است که بگوییم: مشتق پتانسیل الکتریکی در یک جهت خاص، میدان الکتریکی را در آن جهت به ما میدهد.
مثال ۳
در مثال ۲ پتانسیل الکتریکی حاصل از حلقهای باردار، در فاصله مشخصی از آن بدست آمد. با توجه به پتانسیل الکتریکی محاسبه شده، میدان الکتریکی در همان فاصله چقدر است؟
همانطور که در بالا نیز بیان کردیم با محاسبه گرادیان پتانسیل، میدان الکتریکی از جهات مختصات بدست میآید. البته در این مثال با توجه به اینکه میدان تنها در جهت z وجود دارد، بنابراین میتوان با محاسبه مشتق جزئی میدان در همین راستا، میدان را بدست آورد. میدان الکتریکی در راستای z برابر است با:
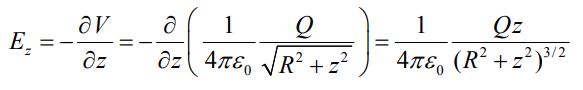
در مطلب میدان الکتریکی نیز همین عدد بدست آمد. مفهوم پتانسیل الکتریکی پیشنیازی ضروری برای مباحث پیشرفتهتر الکتریسیته، همچون الکترومغناطیس، الکترودینامیک و ... محسوب میشود. از این رو برای تسلط بیشتر به موضوع این آموزش برایتان بسیار مفید خواهد بود. همچنین در صورت علاقهمندی به مباحث مرتبط با فیزیک پایه آموزشهای زیر به شما پیشنهاد میشود:
- مجموعه آموزشهای فیزیک
- مجموعه آموزشهای دروس مهندسی برق
- آموزش فیزیک پایه ۲
- میدان الکتریکی (Electric Field) چیست؟ -- از صفر تا صد
- قانون کولن چیست؟ -- به زبان ساده











آقا محمد دستت درد نکنه خیلی خوب بود
آقا مرسی واقعا استفاده کردم
سلام ممنون از شما، برای تصویر دوم قبل از تصویر عنوان کردید(مطابق با شکل زیر تصور کنید که نیروی وزن، جرم m را از ارتفاع A به B جابجا میکند.) ایا نیاید گفت تصور کنید نیروی خارجی جرم را از ارتفاع aبه bجابجا میکند،من متوجه نمیشم اخه نیروی وزن جسم رو از ارتفاع بالا به پایین میکشد نه از پایین به بالا ممنون میشم راهنمایی کنید
خیلی عالی بود. جامع و کامل
اقا دمت خیلی گرم خسته نباشی کلی تو کوییزم کمک کردی