متغیر تصادفی و توزیع دریکله (Dirichlet Distribution) — به زبان ساده

در آمار و تئوری احتمالات، متغیر تصادفی و «توزیع دریکله» (Dirichlet Distribution) جزء توابع توزیع با اهمیت محسوب می‌شود زیرا در استنباط بیزی می‌تواند به عنوان توزیع مزدوج دوجمله‌ای (Binomial Distribution) قرار گیرد. بنابراین آگاهی از خصوصیات آن می‌‌تواند در حل بسیاری از مسائل استنباط آماری موثر باشد. این توربع به صورت چند متغیره تک پارامتری بوده و به صورت $$Dir(\alpha)$$‌ نشان داده می‌شود.

از آنجایی که این توزیع در حالت چند متغیره می‌تواند تعمیم برای توزیع بتا در نظر گرفته شود، گاهی به آن توزیع بتای چند متغیره (Multivaraite Beta Distribution - MBD) نیز گفته می‌شود. نام این توزیع از نام ریاضی‌دان بزرگ آلمانی «پیتر دریکله» (Peter Gutav Lejeune Dirikhlet) گرفته شده است. این توزیع را گاهی «دیریکله» نیز می‌نامند.

برای درک مفاهیم به کار رفته در این نوشتار مطالعه مطالب توزیع های آماری گاما و بتا — مفاهیم و کاربردها و متغیر تصادفی و توزیع چند جمله ای (Multinomial Distribution) — به زبان ساده ضروری به نظر می‌رسد. همچنین خواندن مطلب احتمال پسین (Posterior Probability) و احتمال پیشین (Prior Probability) — به زبان ساده خالی از لطف نیست.

متغیر تصادفی و توزیع دریکله

این توزیع به صورت چند متغیره است. بنابراین تکیه‌گاه آن نیز به صورت یک بردار نمایش داده ‌می‌شود. فرض کنید متغیر تصادفی $$X$$ دارای $$K$$ بعد باشد.

فیلم آموزش شبیه سازی متغیرهای تصادفی و وابسته در متلب در فرادرس

کلیک کنید

در این صورت تکیه‌گاه متغیر تصادفی دریکله به صورت زیر نوشته می‌شود.

$$\large x_1,x_2,\cdots,x_K, \;\;x_i\in (0,1),\;\;\sum_{i=1}^Kx_i=1$$

این روابط نشان می‌دهند که متغیر تصادفی دریکله $$K$$ بعدی بوده و مجموع مقادیر مولفه‌های آن برابر با یک است. از طرفی مشخص است که مقادیر بردار متغیر تصادفی دریکله در بازه صفر تا یک تغییر می‌کند. به این ترتیب متغیر تصادفی $$X$$ با این خصوصیات را با منتغیر تصادفی با توزیع دریکله از مرتبه $$K$$ می‌نامیم.

نکته: مشخص است که مقدار $$K$$ از مجموعه اعداد طبیعی است. معمولا مقدار $$K$$ را بزرگتر یا مساوی با ۲ در نظر می‌گیرند. در ادامه مشخص می‌شود که به ازاء $$K=1$$ این توزیع با توزیع بتا یکسان خواهد شد.

متغیر تصادفی $$X=(X_1,X_2,\cdots,X_K)$$ را دارای توزیع دریکله گویند اگر تابع احتمال (تابع چگالی احتمال) آن به صورت زیر باشد. در این صورت می‌گوییم متغیر تصادفی $$X$$ دارای توزیع دریکله مرتبه $$K$$ با پارامتر $$\alpha=(\alpha_1,\alpha_2,\cdots,\alpha_K)$$ است و این عبارت را به صورت نماد ریاضی $$X\sim Dir_k(\alpha)$$ نشان می‌دهیم.

$$\large {\displaystyle f\left(x_{1},\ldots ,x_{K};\alpha _{1},\ldots ,\alpha _{K}\right)={\frac {1}{\mathrm {B} ({\boldsymbol {\alpha }})}}\prod _{i=1}^{K}x_{i}^{\alpha _{i}-1}}$$

در اینجا منظور از $$\mathrm {B} ({\boldsymbol {\alpha }})$$ تابع بتای چند متغیره است که به شکل نسبت توابع گاما و مطابق با رابطه زیر محاسبه می‌شود.

$$\large {\displaystyle \mathrm {B} ({\boldsymbol {\alpha }})={\frac {\prod _{i=1}^{K}\Gamma (\alpha _{i})}{\Gamma \left(\sum _{i=1}^{K}\alpha _{i}\right)}},\qquad {\boldsymbol {\alpha }}=(\alpha _{1},\ldots ,\alpha _{K})}$$

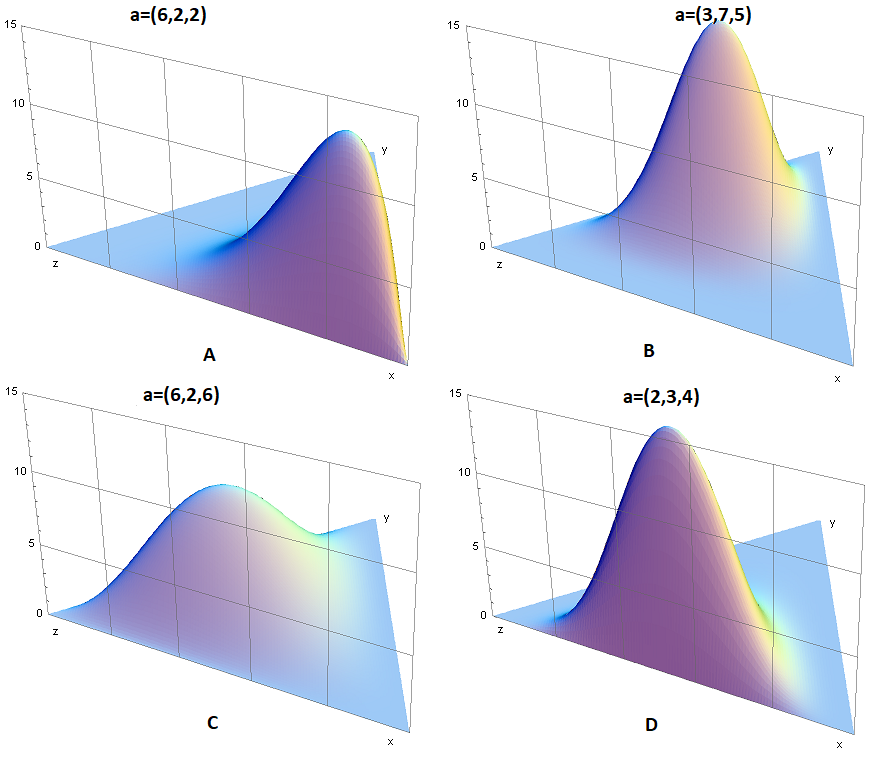
همانطور که مشخص است این توزیع دارای یک پارامتر چند متغیره $$\alpha$$ است که براساس آن مختصات مرکز (امید ریاضی و نما) توزیع تعیین می‌شود. نمودار تابع چگالی این متغیر تصادفی در سه بُعد برای چهار شکل مختلف از پارامتر $$\alpha$$ در تصویر زیر دیده می‌شود.

حالت خاص توزیع دریکله

یکی از حالت‌های خاص برای توزیع دریکله، زمانی است که بردار پارامتر این توزیع مقادیر یکسانی داشته باشد. در چنین حالتی، توزیع دریکله را «متقارن» (Symmetric) می‌نامند. به این ترتیب می‌توان تابع چگالی این متغیر تصادفی را با تنها یک پارامتر عددی ($$\alpha$$) مشخص کرد. در این حالت پارامتر $$\alpha$$ را با نام «پارامتر تراکم» (Concentration) می‌شناسند. رابطه محاسباتی برای تابع چگالی متغیر تصادفی «دریکله متقارن مرتبه $$K$$»  به صورت زیر نوشته می‌شود.

$$\large f(x_{1},\dots ,x_{K-1};\alpha )={\frac {\Gamma (\alpha K)}{\Gamma (\alpha )^{K}}}\prod _{i=1}^{K}x_{i}^{\alpha -1}$$

اگر پارامتر  $$\alpha=۱$$ باشد،‌ توزیع دریکله متقارن به توزیع یکنواخت استاندارد تبدیل خواهد شد. به این معنی که این توزیع در هر بعد به صورت یک توزیع گسسته یکنواخت تک متغیره خواهد بود. چنین توزیعی را گاهی به نام Flat Dirichlet Distribution نیز می‌شناسند.

اگر بردار $$X=(X_1,X_2,\cdots,X_K)$$ دارای توزیع دریکله با پارامتر $$\alpha=(\alpha_1,\alpha_2,\cdots,\alpha_K)$$ باشد و  $$\alpha_0$$‌ را به صورت $$\alpha_0=\sum_{i=1}^K\alpha_i$$ در نظر بگیریم، آنگاه هر یک از ابعاد متغیر تصادفی $$X$$ یعنی $$X_1,X_2,\cdots,X_K$$ دارای توزیع بتا هستند. به این ترتیب رابطه زیر برقرار است.

$$\large X_i\sim Beta(\alpha_i, \alpha_0-\alpha_i)$$

همچنین اگر $$K=1$$‌ در نظر گرفته شود، توزیع دریکله به توزیع بتا تبدیل خواهد شد. به این ترتیب خواهیم داشت:

$$\large X\sim Dir_{k=1}(\alpha_1) \rightarrow X \sim Beta(\alpha,1)$$

خصوصیات متغیر تصادفی دریکله

با توجه به مفهوم امید ریاضی و واریانس متغیر تصادفی، می‌توان برای متغیر تصادفی دریکله، این خصوصیات را محاسبه کرد. به این ترتیب خواهیم داشت:

$$\large  E(X_i)=\dfrac{a_i}{a_0}$$

از طرفی واریانس نیز در هر بعد مطابق با رابطه زیر بدست می‌آید.

$$\large  Var(X_i)=\dfrac{a_i(a_0-a_i)}{a^2_0(a_0+1)}$$

همیچنین کوواریانس بین متغیرهای تصادفی $$X_i, X_j$$ به صورت زیر است.

$$\large Cov(X_i,X_j)=\dfrac{(-a_ia_j)}{a_0^2(a_0+1)}$$

نکته: توجه داشته باشید که ماتریس حاصل از کوواریانس برای متغیر تصادفی دریکله، منفرد، یعنی معکوس‌پذیر است.

از طرفی «نما» (Mode) این توزیع به ازاء $$a_i>1$$ برابر است با $$\large {\displaystyle x_{i}={\frac {\alpha _{i}-1}{\sum _{k=1}^{K}\alpha _{k}-K}}}$$.

توزیع دریکله به صورت توزیع مزدوج پیشین توزیع چندجمله‌ای است. به این ترتیب اگر متغیر تصادفی $$X$$ دارای توزیع چندجمله‌ای (Multinomial- MN) با احتمالات $$p=(p_1,p_2,\cdots,p_K)$$ و توزیع پیشین پارامتر آن (یعنی بردار $$p$$) دارای توزیع دریکله با مرتبه $$K$$ باشد، آنگاه توزیع پسین برای بردار پارامتر $$p$$ نیز باز توزیع دریکله خواهد بود. این موضوع را به کمک روابط زیر نشان می‌دهیم.

$$\large {\displaystyle {\begin{array}{rcccl}{\boldsymbol {\alpha }}&=&\left(\alpha _{1},\ldots ,\alpha _{K}\right)&=&{\text{concentration hyperparameter}}\\\mathbf {p} \mid {\boldsymbol {\alpha }}&=&\left(p_{1},\ldots ,p_{K}\right)&\sim &\operatorname {Dir} (K,{\boldsymbol {\alpha }})\\\mathbb {X} \mid \mathbf {p} &=&\left(\mathbf {x} _{1},\ldots ,\mathbf {x} _{K}\right)&\sim &\operatorname {MN} (K,\mathbf {p} )\end{array}}}$$

به این ترتیب با توجه به روابط بالا، خواهیم داشت:

$$\large {\displaystyle {\begin{array}{rcccl}\mathbf {c} &=&\left(c_{1},\ldots ,c_{K}\right)&=&{\text{number of occurrences of category }}i\\\mathbf {p} \mid \mathbb {X} ,{\boldsymbol {\alpha }}&\sim &\operatorname {Dir} (K,\mathbf {c} +{\boldsymbol {\alpha }})&=&\operatorname {Dir} \left(K,c_{1}+\alpha _{1},\ldots ,c_{K}+\alpha _{K}\right)\end{array}}}$$

از این رابطه‌ها در حوزه استنباط بیزی بخصوص برای پارامتر احتمال توزیع چندجمله‌ای استفاده می‌شود.

ارتباط با توزیع‌های دیگر

فرض کنید $$Y_1,Y_2,\cdots, Y_K$$ متغیرهای تصادفی مستقل با توزیع گاما باشند. یعنی داشته باشیم:

$$\large {\displaystyle Y_{1}\sim \operatorname {Gamma} (\alpha _{1},\theta ),\ldots ,Y_{K}\sim \operatorname {Gamma} (\alpha _{K},\theta )}$$

می‌دانیم که مجموع این متغیرهای تصادفی نیز دارای توزیع گاما (Gamma Distribution) است. یعنی رابطه زیر برقرار است.

$$\large V=\sum _{i=1}^{K}Y_{i}\sim \operatorname {Gamma} \left(\sum _{i=1}^{K}\alpha _{i},\theta \right)$$

حال متغیر تصادفی $$X$$ که به صورت نسبت $$Y$$ها بر $$V$$ تعریف می‌شود، دارای توزیع دریکله است. یعنی می‌توان توزیع متغیر تصادفی $$X$$ را به صورت زیر در نظر گرفت.

$$\large {\displaystyle X=(X_{1},\ldots ,X_{K})=\left({\frac {Y_{1}}{V}},\ldots ,{\frac {Y_{K}}{V}}\right)\sim \operatorname {Dir} \left(\alpha _{1},\ldots ,\alpha _{K}\right)}$$

از این خاصیت برای شبیه‌سازی یا تولید اعداد تصادفی با توزیع دریکله استفاده می‌شود. بنابراین کافی است مقادیری از $$K$$ متغیر تصادفی گاما تولید کرده و حاصل جمع‌ آن‌ها را محاسبه کنیم، نسبت هر یک از این مقدارها بر حاصل جمع، بردار مقادیر توزیع دریکله خواهد بود.

نکته: با توجه به کوواریانس متغیر تصادفی دریکله، مشخص است که این متغیرهای تصادفی $$X_i$$‌ها مستقل نیستند ولی از طریق نسبت متغیرهای تصادفی مستقل گاما تولید شده‌اند.

کد پایتون که در زیر قابل مشاهده است، شیوه شبیه‌سازی و تولید اعداد تصادفی با توزیع دریکله را مورد بررسی قرار داده است. خروجی این دستورات، یک اعداد تصادفی $$K$$ بعدی با توزیع دریکله است.

1params = [a1, a2, ..., ak]
2sample = [random.gammavariate(a,1) for a in params]
3sample = [v/sum(sample) for v in sample]

تفسیر شهودی از پارامتر توزیع دریکله

همانطور که قبلا اشاره شد، توزیع‌های خانواده دریکله اغلب به عنوان توزیع پیشین در استباط بیزی به کار می‌روند. ساده‌ترین و شاید رایج‌ترین توزیع دریکله، نوع متقارن آن است که در این حالت تمام مقدار بردار پارامترها $$\alpha$$ با یکدیگر برابر هستند. به این ترتیب مشخص است که هیچ یک از مولفه‌های این توزیع نسبت به دیگری دارای اهمیت یا اولویت بیشتری نیست. بنابراین زمانی که هیچ اطلاعات پیشینی از پارامترها نداریم، استفاده از این توزیع مناسب به نظر می‌رسد.

فیلم آموزش متغیرهای تصادفی پیوسته (رایگان) در فرادرس

کلیک کنید

در این حالت، همانطور که در قسمت‌های قبل گفته شد، پارامتر $$\alpha$$، پارامتر تراکم (Concentration) نامیده می شود. اگر فضای نمونه متغیر تصادفی دریکله، به صورت گسسته در نظر گرفته شود و تابع احتمال را به صورت میزان احتمال در هر نقطه محسوب کنیم، می‌توان پارامتر تراکم را به عنوان میزان چگالی یا تراکم (Concentration) احتمال در هر بعد در نظر گرفت. اگر مقدار این پارامتر بسیار کمتر از ۱ باشد، بیشترین جرم احتمال روی تعداد مولفه‌های کمتری متمرکز شده است. همچنین اگر مقدار پارامترها بسیار بزرگتر از ۱ باشند، به نظر می‌رسد که جرم احتمال روی همه مولفه‌ها بطور یکسان پخش شده است و توزیع حاصل، مشابه توزیع یکنواخت خواهد شد.

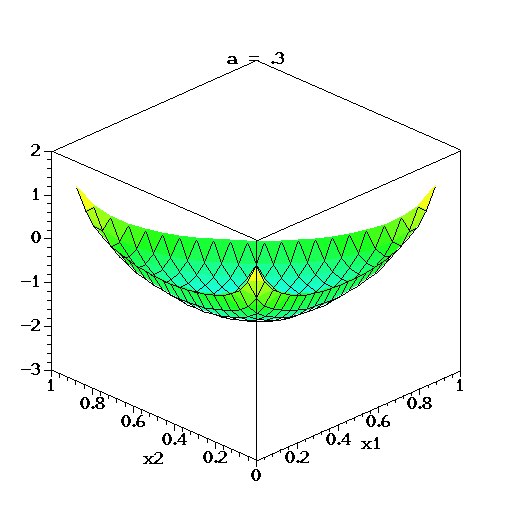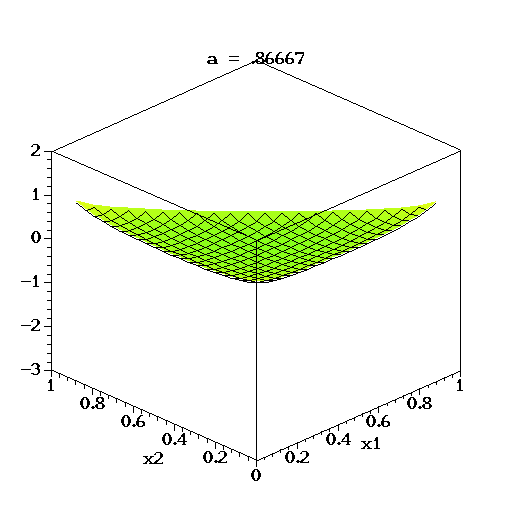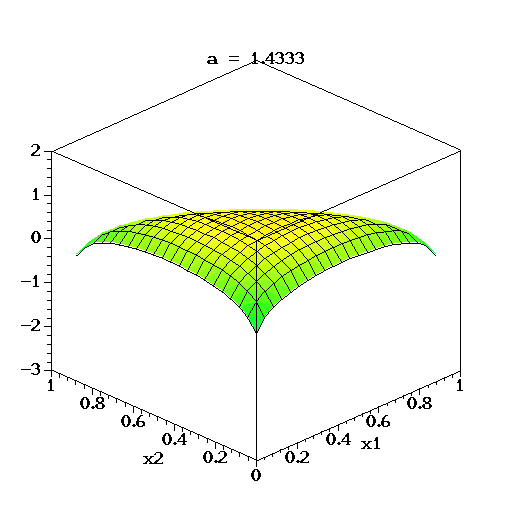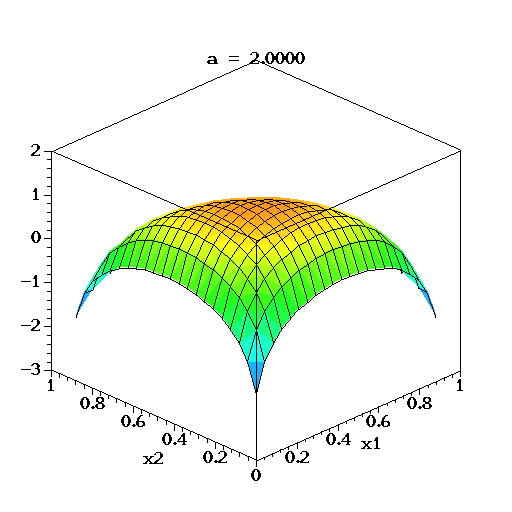
در تصویر متحرک زیر نیز برای متغیر تصادفی سه بُعدی دریکله، لگاریتم تابع چگالی برای مقدارهای مختلف پارامتر $$\alpha=(0.3,0.3,0.3)$$ تا $$\alpha=(2,2,2)$$ ترسیم شده‌ است. البته توجه داشته باشید که تغییرات بردار پارامترها در این ترسیم‌ها همگی یکسان است.

اگر مطلب بالا برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش‌های یادگیری ماشین و بازشناسی الگو
• آموزش آمار و احتمال مهندسی
• تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده
• توزیع های آماری گاما و بتا — مفاهیم و کاربردها
• احتمال پسین (Posterior Probability) و احتمال پیشین (Prior Probability) — به زبان ساده

^^