برازش منحنی (Curve Fitting) – به زبان ساده (+ دانلود فیلم آموزش گام به گام)
به فرآیند تعیین یک منحنی یا تابع ریاضی که بیشترین شباهت را به دادهها داشته باشد اصطلاحا «برازش منحنی» (Curve Fitting) گفته میشود. اغلب برای نمایش رابطه بین متغیرها از نمودار استفاده میکنیم. این کار کمک میکند که رابطه بین دو متغیر عددی بهتر نمایان شود. این گونه نمودارها با استفاده از نقاط دو یا چندبعدی در مختصات دکارتی یا قطبی قادر به نمایش رابطه بین دادهها هستند. این کار به «تصویرسازی دادهها» (Data Visualization) و درک اطلاعاتی که در آنها وجود دارد کمک شایانی میکند. در این گونه نمودارها اغلب محور افقی بیانگر متغیر x و محور عمودی نیز مقدار y را نشان میدهد.

در این مطلب به بررسی روشهای برازش منحنی به کمک چند جملهایها پرداخته و سعی میکنیم به کمک ترسیم نمودار دادهها و منحنی برازش شده این روشها را فرا گیریم. همچنین در ادامه با استفاده از مثالهایی به بررسی این روشها میپردازیم. میتوانید برای آشنایی با شیوه رسم نمودار به مطلب نمایش و رسم نمودار برای دادهها — معرفی و کاربردها مراجعه کنید.
برازش منحنی (Curve fitting)
معرفی منحنی یا تابعی که از بیشتر نقطهها یا دادههای موجود عبور یا کمترین فاصله را از آنها داشته باشد برازش منحنی نامیده میشود. اگر این منحنی از همه نقاط موجود عبور کرده باشد، دقت برازش بیشترین مقدار را براساس دادههای موجود، خواهد داشت. اغلب در چنین حالتهایی، محقق قادر است تا براساس نمودار دست به پیشبینی بزند و برای نقاطی که در مجموعه داده وجود ندارد، نقطهای را به عنوان برآورد بیابد. اگر این نقطه در دامنه نقاط مجموعه داده باشد، عمل پیشبینی را «درونیابی» (Interpolation) مینامند و در حالتی که این نقطه خارج از دامنه نقاط باشد، «برونیابی» (Extrapolation) نامیده میشود. مسلما هیچ یک از این دو کار بدون خطا صورت نخواهند گرفت.
گاهی ممکن است بهترین منحنی یا تابعی که بیشترین نزدیکی (کمترین خطا) نسبت به نقاط موجود را دارد، به عنوان بهترین نمودار یا منحنی برازش انتخاب کنیم. در این حالت عمل «هموارسازی» (Smoothing) صورت گرفته است. در حقیقت گاهی روشهای رگرسیونی را یکی از تکنیکهای هموارسازی محسوب میکنند.
در ادامه به روشهای درونیابی که توسط چند جملهایها قابل اجرا هستند، پرداختهایم و بحث در مورد مباحث برونیابی و یا هموارسازی را به مطالب بعدی موکول میکنیم.
روش برازش منحنی به کمک توابع چند جملهای
همانطور که میدانید حالت کلی چند جملهای درجه n به صورت زیر است:
با توجه به تعداد نقاطی که در برازش منحنی به کار گرفته میشوند، میتوان از چند جملهای با درجه مناسب کمک گرفت. برای مثال به منظور برازش یک منحنی با n نقطه میتوان از یک چند جملهای با درجه n-1 استفاده کرد.
برازش به کمک خط (چند جملهای درجه ۱)
تابع y=ax+b معادله یک خط راست است که در آن a شیب خط و b عرض از مبدا نامیده میشود. این معادله بهترین برازش را برای دو نقطه دارد زیرا یک خط راست توسط دو نقطه از آن قابل نمایش است و از دو نقطه فقط یک خط راست میتوان عبور داد. پس معادله خط راست بهترین برازش را برای دو نقطه خواهد داشت. به این ترتیب میتوان هر دو نقطه مجاور را به کمک یک خط به یکدیگر متصل نمود و یک نمودار با خطوط شکسته برای درونیابی تابع مورد نظر ایجاد کرد.
مثال ۱
هفت نقطه در مختصات دکارتی طبق جدول زیر ثبت شدهاند. میخواهیم یک تابع یا منحنی برازش برای آنها به کمک معادله چندین خط ایجاد کنیم.
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| f(x) | 0 | 0.8415 | 0.9093 | 0.1411 | −0.7568 | −0.9589 | −0.2794 |
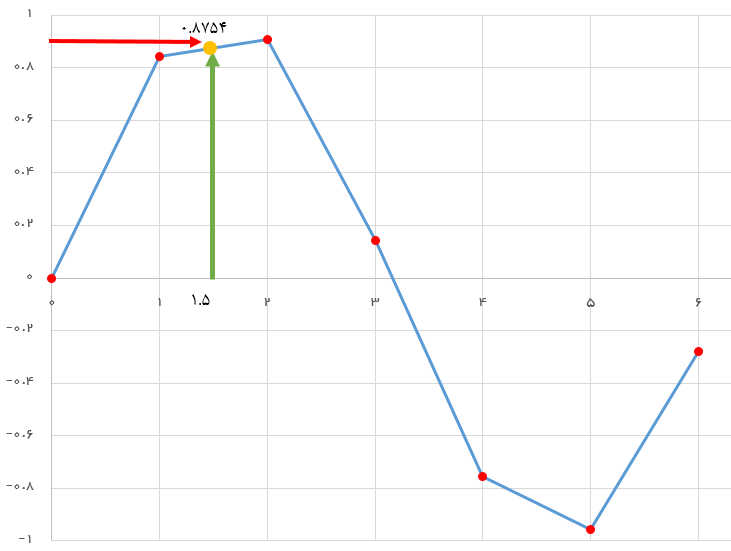
به کمک معادله یک خط که از هر دو نقطه مجاور میگذرد، منحنی و تابع مربوط به برازش این منحنی را ایجاد میکنیم. میدانیم که معادله خطی که از بین دو نقطه و میگذرد به صورت زیر است:
بنابراین میتوان معادله خطوط را بدست آورد و برای مثلا مقدار برآورد y را محاسبه کرد. معادله خطی که از دو نقطه و میگذرد به صورت زیر است:
با جایگذاری مقدار 1.5 در متغیر x برآورد مقدار y محاسبه میشود:
برازش به کمک چند جملهای درجه n
چند جملهای حالت کلیتری برای درونیابی بوسیله معادله خط است. به این ترتیب برای درونیابی، به جای استفاده از یک خط راست، میتوان از یک منحنی که توسط یک چند جملهای ایجاد میشود، استفاده کرد.
نکته: معادله خط نوع خاصی از چند جملهای محسوب میشود که درجه آن ۱ است. استفاده از چند جملهای درجه ۲ میتواند بهترین برازش را برای سه نقطه داشته باشد. به این ترتیب برای برازش n نقطه میتوان از یک چند جملهای درجه استفاده کرد.
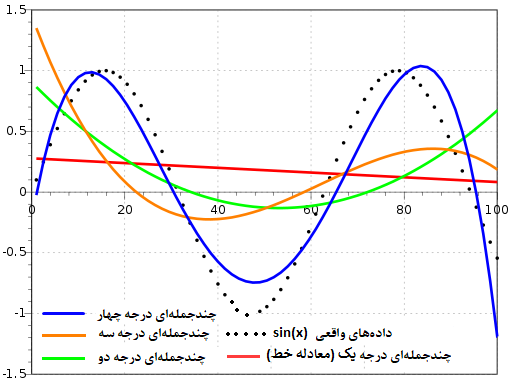
برای مثال تصویر زیر درونیابی برای تابع توسط چند جملهایهای درجه ۱، ۲، ۳ و ۴ را نشان میدهد. مشخص است که هر کدام از این چند جملهایها در دو، سه، چهار و پنج نقطه منحنی را قطع کردهاند.
در روشهای درونیابی چند جملهای، معمولا ضرایب مربوطه به کمک تکنیکهای عددی برآورد شده و کار برازش برای منحنی انجام میشود.
مثال ۲
برای نقاط مربوط به مثال 1 با توجه به یک چند جملهای درجه ۶ ضرایب و فرم چند جملهای به صورت زیر درآمده است.
برای برآورد مقدار منحنی در نقطه x=1.5 کافی است این چند جملهای را در این نقطه محاسبه کنیم.
بار محاسباتی برای چنین روشهایی نسبت به درونیابی خطی بسیار زیاد است و در حالتی که نقاط منحنی اصلی زیاد باشد درجه چند جملهای بزرگ شده و محاسبات به کندی صورت میگیرند. برای سرعت بخشیدن به محاسبات، روش دیگری که ترکیبی از حالت خطی و چند جملهای است به نام Spline به کار میرود.
درونیابی Spline
همانطور که گفته شد، در درونیابی خطی، برای هر فاصله معادله یک خط در نظر گرفته شد. در روش درونیابی Spline برای چنین فاصلههایی از یک چند جملهای با درجه کم (مثلا ۲ یا ۳) استفاده میکنند. به این ترتیب خطای حاصل از درونیابی خطی کاهش یافته و منحنی برازش، هموارتر میشود.
این کار ترکیبی از درونیابی خطی را با روش چند جملهای ارائه میکند. در نتیجه، سرعت محاسبات افزایش یافته و خطای حاصل از درونیابی کاهش مییابد. برای آشنایی با شیوه درونیابی Spline به مثال زیر توجه کنید.
مثال ۳
دادههای مربوط به مثال ۱ را در نظر بگیرید. در هر فاصله، یک چند جملهای درجه ۳ در نظر گرفته شده و به کمک روشهای عددی ضرایب آن نیز برآورد شدهاند. در چنین حالتی تابع چند ضابطهای زیر بدست آمده است.
حال اگر بخواهیم مقدار تابع را در نقطه 1.5 برآورد کنیم، از دومین ضابطه کمک گرفته و با جایگذاری x با 1.5 مقدار y را برآورد میکنیم. حاصل کار برابر خواهد بود با 0.9943 که با مقدار برآورد شده توسط روش خطی تفاوت دارد.
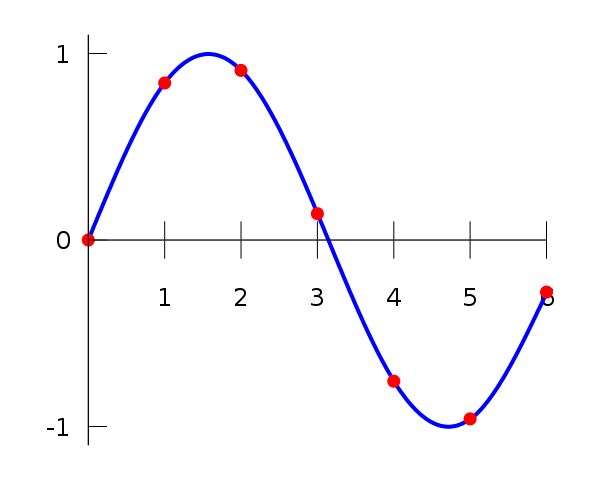
همانطور که در نمودار دیده میشود، منحنی برازش شده از همه شش نقطه میگذرد و بهترین برآورد را برای نقاط درونی منحنی خواهد داشت.
اگر به فراگیری مباحث مشابه مطلب بالا علاقهمند هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
- مجموعه آموزش های SPSS
- مجموعه آموزشهای نرمافزارهای آماری
- آموزش همبستگی و رگرسیون خطی در SPSS
- مهمترین الگوریتمهای یادگیری ماشین (به همراه کدهای پایتون و R) — بخش دوم: رگرسیون خطی
- آموزش یادگیری ماشین
- رگرسیون خطی — مفهوم و محاسبات به زبان ساده
^^













در صورتیکه بخوایم این نمودار رو تحت عنوان سورس به سیمولینک بدیم باید چیکار کنیم؟