تغییر طول غیر یکنواخت سازه های معین استاتیکی — به زبان ساده

اگر اعمال بار بر روی یک میله الاستیک خطی با سطح مقطع یکنواخت تنها بر روی نقاط انتهایی آن صورت گیرد، میزان تغییر طول میله از رابطه δ=PL/EA به دست می‌آید. در مبحث «تغییر طول عضوهای تحت بار محوری»، تأثیر بارهای محوری بر روی تغییر شکل میله‌های منشوری در شرایط بارگذاری یکنواخت را به طور مفصل مورد بررسی قرار دادیم. در این مقاله، نحوه استفاده از رابطه δ در شرایط بارگذاری غیر یکنواخت (بارگذاری غیر یکنواخت، میله‌های چندبخشی و سطح مقطع‌های متغیر) را مورد تحلیل قرار خواهیم داد. در انتها نیز به منظور آشنایی بیشتر شما با نحوه تحلیل این شرایط، به تشریح دو مثال کاربردی خواهیم پرداخت.

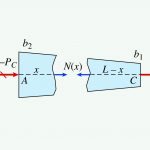
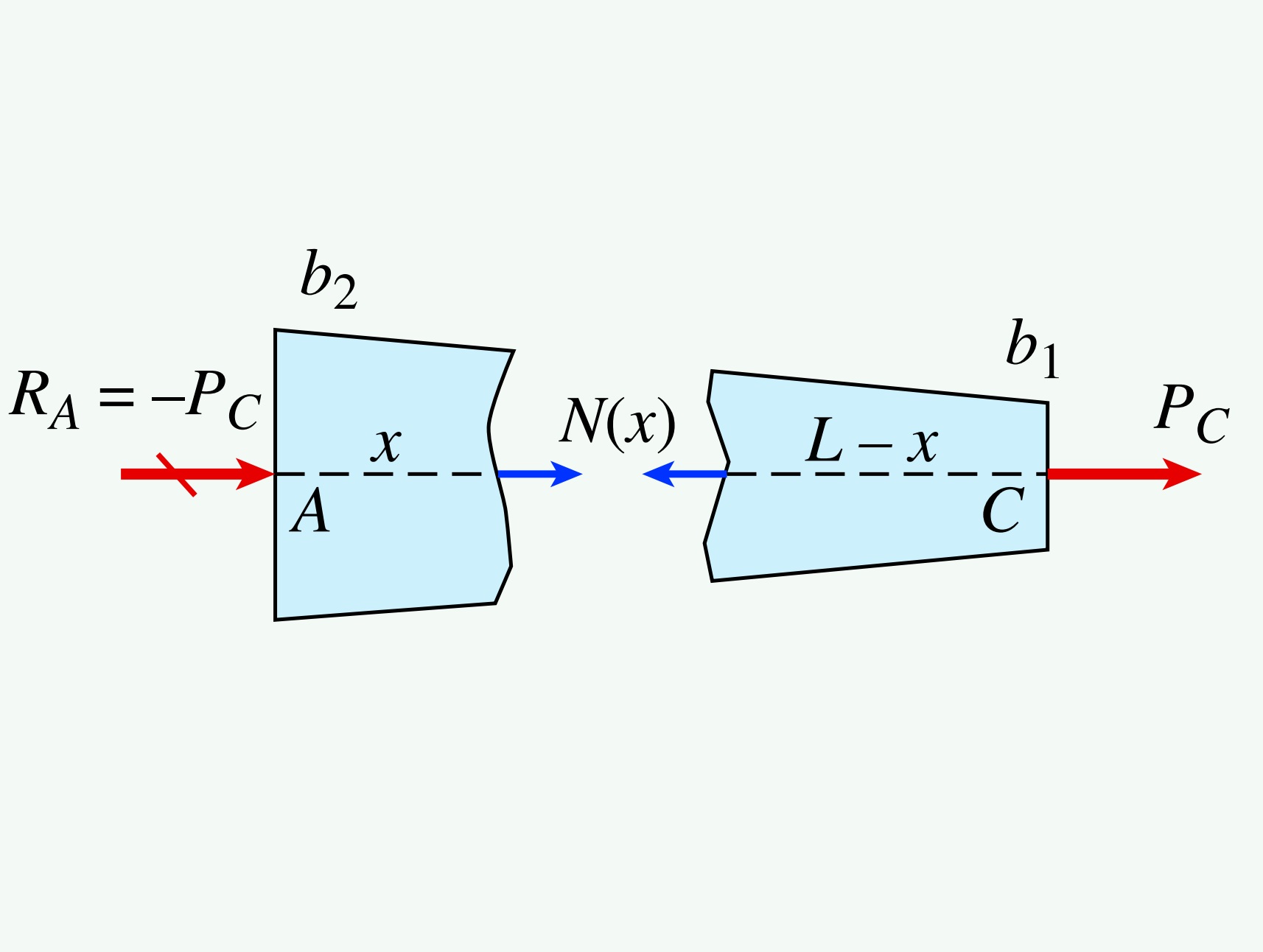
اعمال بارهای محوری نامعین بر روی میله‌ها

شکل زیر را در نظر بگیرید. فرض کنید که نقاط میانی یک میله منشوری همانند این شکل در معرض یک یا چند بار محوری قرار گرفته‌اند. در این شرایط، میزان تغییر طول کلی میله از جمع جبری تغییرات به وجود آمده در هر بخش آن به دست می‌آید. به منظور محاسبه این تغییر طول باید مراحل زیر را دنبال کنید:

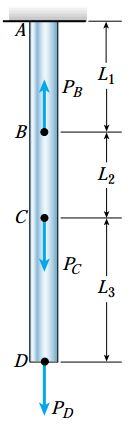
میله‌ای که چند بارِ خارجی بر روی نقاط میانی آن اعمال می‌شوند.

• گام اول: مشخص کردن بخش‌های مختلف میله (BC ،AB و CD) با عنوان بخش‌های 1، 2 و 3

فیلم آموزش مقاومت مصالح – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

• گام دوم: تعیین نیروهای داخلی N₂ ،N₁ و N₃ در بخش‌های 1، 2 و 3 با استفاده از رسم نمودارهای جسم آزاد (شکل زیر). توجه داشته باشید که به منظور ایجاد تمایز بین نیروهای داخلی و خارجی، نیروهای داخلی با حرف N و بارهای خارجی با حرف P نمایش داده می‌شوند.

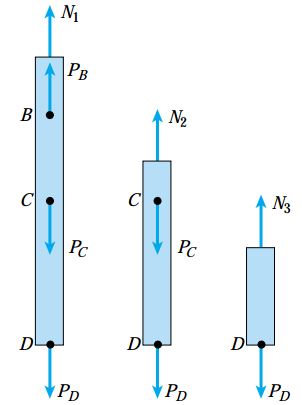
با جمع نیروهای عمودی در نمودارهای بالا، معادلات تعادل زیر به دست می‌آیند:

در این معادلات، علامت مثبت برای نیروهای داخلی کششی و علامت منفی برای نیروهای داخلی فشاری در نظر گرفته می‌شود.

• گام سوم: تعیین تغییرات طول هر بخش با استفاده از روابط زیر:

L₂ ،L₁ و L₃: طول بخش‌های 1، 2 و 3؛ EA: صلبیت محوری میله

• گام چهارم: جمع تغییر طول‌های δ₂ ،δ₁ و δ₃ به منظور تعیین تغییر طول ایجاد شده در کل میله (δ):

همان‌گونه که قبلاً نیز اشاره شد، مقادیر تغییر طول هر بخش به صورت جبری با هم جمع می‌شوند (علامت مثبت برای افزایش طول و علامت منفی برای کاهش طول).

میله‌های متشکل از چند بخش منشوری

اگر میله‌ای از چندین بخش منشوری با ابعاد، مواد تشکیل‌دهنده یا نیروهای متفاوت تشکیل شده باشد، تعیین تغییر طول به وجود آمده در کل میله با استفاده از روش معرفی شده در بخش قبل صورت می‌گیرد.

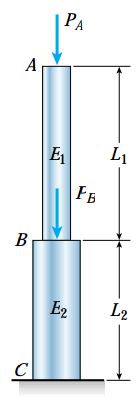
میله‌ای متشکل از دو بخش منشوری با نیروهای محوری، ابعاد و مواد تشکیل‌دهنده متفاوت

رابطه تغییر طول کل برای این حالت به صورت زیر است:

i: اندیس نام‌گذاری بخش‌های مختلف میله؛ n: تعداد بخش‌ها؛ N_i: نیروی محوری داخلی در بخش i ام

تغییر پیوسته در ابعاد یا بارهای اعمال شده بر روی میله

در برخی از مواقع، نیروی محوری N و مساحت سطح مقطع A به طور پیوسته در راستای محور میله تغییر می‌کنند. نمونه‌ای از این وضعیت در شکل زیر نمایش داده شده است. در این میله، نه‌تنها مساحت سطح مقطع بلکه نیروی محوری نیز در راستای محور طولی میله به طور پیوسته تغییر می‌کند.

فیلم آموزش مقاومت مصالح ۱ و ۲ – مرور و حل مساله در فرادرس

کلیک کنید

با توجه به شکل، بارگذاری دارای دو بخش متفاوت است. تک نیروی P_B بر انتهای میله (در نقطه B) و بارهای توزیع شده (p(x در راستای محور میله اعمال می‌شوند.

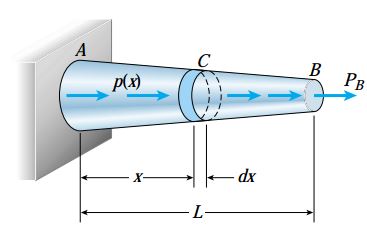
توجه: نیروی توزیع شده بر حسب نیرو بر واحد فاصله (مانند نیوتن بر متر یا پوند بر اینچ) بیان می‌شود. این نوع نیرو توسط عواملی نظیر نیروهای گریز از مرکز، نیروهای اصطکاکی یا وزن میله آویزان در یک موقعیت عمودی به وجود می‌آیند.

در این شرایط نمی‌توانیم رابطه معرفی شده برای حالت قبلی (تغییر طول میله چندبخشی) را مورد استفاده قرار دهیم. در عوض باید ابتدا تغییر طول یک المان کوچک از میله را تعیین کنیم و سپس از طول میله انتگرال بگیریم. به این منظور، المان dx در فاصله x از انتهای چپ میله را در نظر می‌گیریم. نیروی محوری داخلی (N(x در این مقطع (شکل وسط) با کمک معادلات تعادل بخش AC یا CB و رسم نمودار جسم آزاد تعیین می‌شود. به طور کلی، این نیرو تابعی از x است. با مشخص بودن ابعاد میله می‌توان مساحت سطح مقطع (A(x را نیز به صورت تابعی از x نمایش داد.

تغییر طول المان dx با dδ نمایش داده می‌شود. با قرار دادن (N(x به جای P ،dx به جای L و (A(x به جای A در رابطه δ=PL/EA، رابطه زیر برای تعیین dδ به دست می‌آید:

با انتگرال‌گیری از رابطه بالا، تغییر طول کل میله محاسبه می‌شود:

اگر عبارت‌های (N(x و (A(x پیچیده نباشند، انتگرال بالا به صورت تحلیلی قابل حل خواهد بود. در این صورت، یک فرمول برای محاسبه δ به دست می‌آید (مانند مثال 2 در انتهای مقاله). اگرچه، در صورت دشوار یا غیرممکن بودن انتگرال بالا باید از یک روش عددی به منظور حل مسئله استفاده کرد.

محدودیت‌های موجود در روابط ارائه شده

روابط ارائه شده در بخش‌های قبلی تنها برای مواد الاستیک خطی قابل استفاده هستند (وجود پارامتر E در تمام روابط). به علاوه، فرمول δ=PL/EA با فرض یکنواخت بودن تنش بر روی سطح مقطع میله به دست آمده است.

فیلم آموزش مقاومت مصالح ۲ در فرادرس

کلیک کنید

این فرض در میله‌های منشوری صدق می‌کند و در میله‌هایی با سطح مقطع متغیر اعتباری ندارد. به همین دلیل، تنها در صورت کوچک بودن زاویه بین دو طرف این میله‌ها، نتایج به دست آمده از رابطه زیر قابل قبول خواهند بود:

با توجه به بررسی‌های صورت گرفته، اگر زاویه بین دو طرف میله برابر با 20 درجه باشد، تنش به دست آمده از رابطه σ=P/A (در یک مقطع دلخواه)، 3 درصد کمتر از مقدار دقیق تنش به دست آمده از روش‌های پیشرفته خواهد بود. برای زوایای کوچک، خطای محاسبات کمتر می‌شود. بنابراین، هر چه زاویه تغییر سطح مقطع میله کمتر باشد، نتایج به دست آمده از رابطه بالا قابل قبول‌تر خواهد بود. در صورت بزرگ بودن زاویه تغییر سطح مقطع میله، باید از روش‌های دقیق‌تر استفاده کرد.

مثال‌ها

در این بخش، به منظور نمایش نحوه استفاده از روابط ارائه شده برای تعیین تغییر طول میله‌های غیریکنواخت، به تشریح دو مثال می‌پردازیم.

مثال 1

سازه نمایش داده شده در شکل زیر را در نظر بگیرید. در این سازه، انتهای بالایی میله عمودی ABC توسط یک اتصال مفصلی به نقطه A متصل شده است و نیروی P₁ به انتهای پایینی میله اعمال می‌شود.

فیلم آموزش مقاومت مصالح – ویژه رشته عمران در فرادرس

کلیک کنید

یک اتصال مفصلی دیگر، تیر افقی BDE را در نقطه B به میله ABC متصل می‌کند. تکیه‌گاه مفصلی موجود در نقطه D، وظیفه نگهداری تیر BDE را بر عهده دارد. علاوه بر این، نیروی P₂ به نقE اعمال می‌شود.

اگر مدول الاستیسیته P₁=2100lb ،E=29x10⁶ و P₂=5600lb باشد، جابجایی عمودی δ_C در نقطه C چقدر خواهد بود؟ مشخصات هندسی میله و تیر عبارت‌اند از:

• L₁=20in: طول بخش بالایی میله عمودی (AB)
• A₁=0.25in²: مساحت سطح مقطع AB
• L₂=34.8in: طول بخش بالایی میله عمودی (BC)
• A₂=0.15in²: مساحت سطح مقطع BC
• a=28in: طول بخش سمت راست تیر BDE
• b=25in: طول بخش سمت چپ تیر BDE

تعیین نیروهای محوری درون میله ABC

با توجه به پیکربندی سازه می‌توان مشاهده کرد که جابجایی عمودی نقطه C با تغییر طول میله ABC برابر است. بنابراین برای شروع حل مسئله، باید نیروهای محوری درون هر دو بخش این میله را تعیین کنیم. نیروی محوری N₂ در بخش پایینی میله با بارِ P برابر است. نیروی محوری N₁ در بخش بالایی میله نیز در صورت مشخص کردن عکس‌العمل عمودی در نقطه A یا تعیین نیروی وارد شده از طرف تیر به میله به دست می‌آید. به منظور تعیین نیروی وارد شده از طرف تیر به میله، نمودار جسم آزاد تیر را رسم می‌کنیم (شکل چپ). P₃، نیروی اعمال شده از طرف میله عمودی به تیر و R_D، عکس‌العمل عمودی در نقطه D را نمایش می‌دهد. با توجه به نمودار جسم آزاد میله عمودی (شکل راست) مشاهده می‌شود که هیچ نیروی افقی بین میله و تیر وجود ندارد. بنابراین، هیچ عکس‌العمل افقی در نقطه D وجود نخواهد داشت.

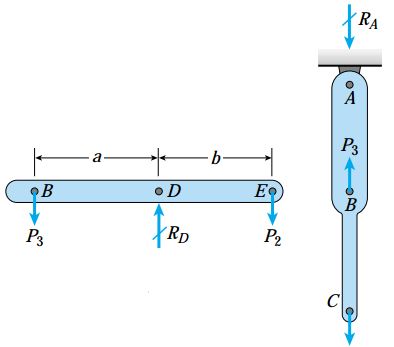
بر اساس نمودار جسم آزاد تیر، با برابر قرار دادن گشتاورهای ناشی از نیروهای P₂ و P₃ حول نقطه D، رابطه زیر به دست می‌آید:

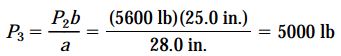
جهت اعمال این نیرو بر روی تیر به صورت رو به پایین و بر روی میله عمودی به صورت رو به بالا است. با مشخص شدن مقدار P₃، عکس‌العمل رو به پایین در نقطه A نیز قابل محاسبه خواهد بود:

بخش بالایی میله عمودی (AB) در معرض نیروی فشاری N₁ قرار دارد (N₁=R_A=2900lb). بخش پایینی این میله (BC) نیز نیروی کششی N₂ را تحمل می‌کند (N₂=P₁=2100lb).

تعیین میزان تغییر طول

با در نظر گرفتن علامت مثبت برای نیروهای کششی، میزان تغییر طول میله ABC را با استفاده از رابطه زیر محاسبه می‌کنیم:

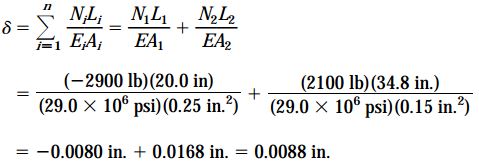
δ: تغییر طول میله ABC

به دلیل مثبت بودن مقدار δ، طول میله افزایش می‌یابد. جابجایی نقطه C نیز با تغییر طول میله برابر است. بنابراین:

مثال 2

شکل زیر، میله‌ای با طول L و سطح مقطع متغیر دایره‌ای را نمایش می‌دهد. یک انتهای این میله (B) ثابت است و انتهای آزاد آن (A) در معرض بارِ کششی P قرار دارد. قطر میله در مقاطع A و B به ترتیب با d_A و d_B نمایش داده می‌شود. با فرض کوچک بودن زاویه تغییر سطح مقطع در طول میله، میزان تغییر طول میله بر اثر اعمال بارِ P را محاسبه کنید.

در این مثال، مقدار نیروی محوری در طول میله ثابت است. با این وجود، مساحت سطح مقطع بین دو انتهای میله به طور پیوسته تغییر می‌کند. بنابراین، برای تعیین تغییر طول کل میله باید از روش انتگرال‌گیری استفاده کنیم.

تعیین مساحت سطح مقطع

اولین قدم برای حل این مسئله، تعیین رابطه معرف مساحت سطح مقطع (A(x در نقاط مختلف میله است. به این منظور باید یک مبدأ برای مختصات x در نظر بگیریم. دو روش برای این کار وجود دارد. در روش اول می‌توان انتهای آزاد میله (A) را به عنوان مبدأ مختصات در نظر گرفت. در روش دوم، با توسعه خطوط اطراف میله، محل برخورد آن‌ها (نقطه O) به عنوان مبدأ مختصات انتخاب می‌شود (شکل زیر). به دلیل ساده‌تر بودن فرآیند انتگرال‌گیری در روش دوم، از این روش برای حل مسئله استفاده می‌کنیم.

فاصله L_A و L_B از نقطه O تا A و B را در نظر بگیرید. با استفاده از تشابه بین مثلث‌ها، نسبت L_A به L_B با نسبت d_A به d_B برابر خواهد بود:

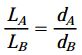
به همین ترتیب، نسبت قطر (d(x در فاصله x از نقطه مبدأ به قطر d_A در انتهای کوچک میله برابر است با:

با جایگذاری رابطه بالا در فرمول مساحت دایره (πd²/4)، رابطه مورد نیاز برای تعیین مساحت سطح مقطع میله در فاصله x از نقطه مبدأ به دست می‌آید:

تعیین تغییر طول میله

اکنون با جایگذاری رابطه (A(x در انتگرال δ، رابطه مورد نیاز برای محاسبه تغییر طول میله تعیین می‌شود:

با انتگرال‌گیری و قرار دادن حدود انتگرال به رابطه زیر می‌رسیم:

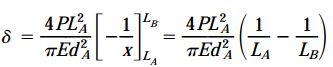
عبارت داخل پرانتز در رابطه بالا را می‌توان به صورت زیر ساده کرد:

با جایگذاری این عبارت ساده‌شده در رابطه قبلی، به رابطه زیر می‌رسیم:

با توجه به اینکه L_A/L_B=d_A/d_B، فرم نهایی رابطه δ به صورت زیر به دست می‌آید:

رابطه بالا، برای محاسبه میزان تغییر طول یک میله مخروطی با سطح مقطع دایره‌ای به کار می‌رود.

توجه: یکی از روش‌های اشتباه و متداول برای حل این مسئله، در نظر گرفتن یک میله منشوری با قطر سطح مقطع میانی میله غیر یکنواخت و محاسبه تغییر طول این میله منشوری به جای تغییر طول میله غیر یکنواخت است.

توجه: اگر یکی از حالت‌های خاص میله مخروطی را با فرض d_A=d_B=d در نظر بگیریم، رابطه δ به صورت زیر ساده می‌شود:

این رابطه با معادله تغییر طول میله منشوری یکسان است. به منظور تأیید صحت رابطه کلی δ در میله‌هایی با سطح مقطع مستطیلی یا شکل‌های دیگر نیز می‌توانیم حالت‌های خاص مسئله را در نظر بگیریم و رابطه به دست آمده را با رابطه δ=PL/EA مقایسه کنیم.

اگر این روابط با یکدیگر تطابق نداشته باشند، رابطه کلی صحیح نخواهد بود. در صورت تطابق بین دو رابطه، قطعیت ما در مورد صحت رابطه کلی افزایش می‌یابد اما احتمال عدم صحت آن از بین نمی‌رود. به عبارت دیگر، بررسی این تطابق یک شرط لازم برای تشخیص صحت رابطه کلی به شمار می‌رود اما این شرط به تنهایی کافی نیست.

^^