فرادرسمفاهیم مقدماتی حسابان (بخش اول) — به زبان ساده
ما معمولاً شکل‌ها، فرمول‌ها و موقعیت‌های مختلف را با مقادیرشان بررسی می‌کنیم؛ اما حسابان دو قدرت ماورایی در اختیار ما قرار می‌دهد تا در این زمینه‌ها عمیق‌تر شویم. این دو قدرت شامل بینایی اشعه ایکس و بینایی تایم‌لپس هستند که در ادامه معرفی می‌کنیم.
بینایی اشعه ایکس (X-Ray): به کمک این قدرت می‌توان قطعه‌های پنهان درون یک الگو را مشاهده کرد. ما در این موارد تنها درخت را نمی‌بینیم، بلکه حلقه‌های تشکیل دهنده آن که در طی رشد ایجاد شده‌اند را نیز مشاهده می‌کنیم.
بینایی تایم-لپس (Time-Lapse): به کمک حسابان می‌توانید مسیر آینده شیئی که پیش روی شما قرار دارد را نیز مشاهده کنید. ماه را در آسمان می‌بینید و می‌دانید که در طی چند روز آینده به صورت بدر کامل خواهد بود؛ اما در روزهای پس از آن نزدیک به افق خواهد بود و به رنگ تیره‌تر درمی‌آید. بنابراین می‌توانید برنامه عکاسی خود را تنظیم کنید.
اینک سؤال آن است که حسابان از چه نظر مفید است؟ تصور کنید قدرت بینایی اشعه ایکس یا تایم‌لپس را در اختیار داشته باشید. در مورد یک شیء یا سناریو چگونه می‌توان از آن بهره گرفت؟ در این مسیر چه اتفاق‌هایی رخ می‌دهد؟
مشاهده الگوها از طریق حسابان به صورت گام به گام
شاید از خود بپرسید بینایی اشعه ایکس و تایم-لپس چه وجه اشتراکی دارند؟ پاسخ این است که هر دوی آن‌ها الگوها را به صورت گام به گام بررسی می‌کنند. یک تصویر اشعه ایکس برش‌های منفرد درون یک شیء را نشان می‌دهد و تصاویر تایم‌لپس نیز وضعیت‌های مختلف یک پدیده را در کنار هم نمایش می‌دهند.
این وضعیت کاملاً انتزاعی به نظر می‌رسد. در ادامه معادله‌های محیط، مساحت، مساحت سطحی و حجم دایره و کره را بررسی می‌کنیم:
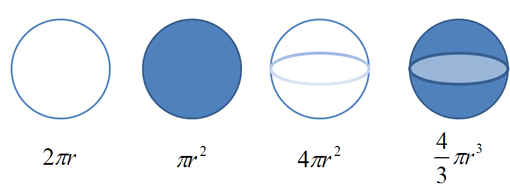
شاید با مشاهده فرمول‌های فوق این تصور را پیدا کنید که آن‌ها با هم مرتبط هستند.
اگر بینایی اشعه ایکس خود را فعال کنیم، می‌توانیم درستی این گزاره را بررسی کنیم. فرض کنید می‌دانیم که محیط دایره برابر با 2πr است و می‌خواهیم معادله مساحت آن را بیابیم. چه می‌توان کرد؟ این سؤال ممکن است دشوار به نظر بیاید، چون گرچه اندازه‌گیری مربع‌ها آسان است؛ اما اندازه یک شکل منحنی را چگونه می‌توان به دست آورد؟
حسابان در این مسیر به ما کمک می‌کند. اگر از بینایی اشعه ایکس خود استفاده کنیم، درک می‌کنیم که یک دیسک در واقع مجموعه‌ای از حلقه‌ها است که کنار هم چیده شده‌اند. به طور مشابه، چنان که در تصویر تنه درخت فوق مشاهده کردید، می‌توانیم از یک نمای «گام به گام» برای محاسبه مساحت دایره استفاده کنیم.
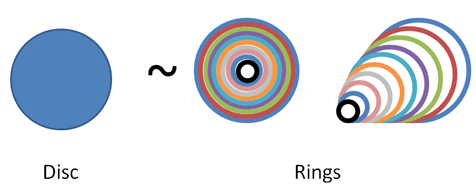
فایده شیوه تصور فوق این است که می‌توانیم آن حلقه‌های تشکیل دهنده دایره را باز کنیم و به صورت خط مستقیم در بیاوریم. بدین ترتیب اندازه‌گیری آن‌ها ساده‌تر خواهد بود.
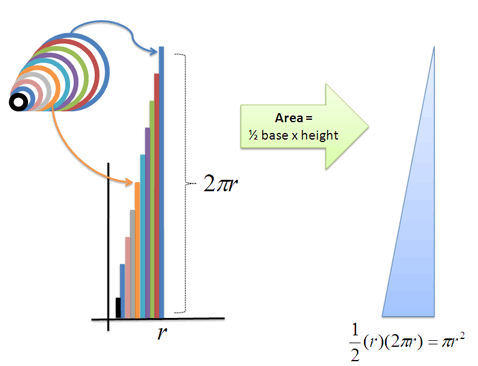
همان طور که می‌بینید دسته‌ای از حلقه‌های باز را داریم که به شکل یک مثلث درآمده‌اند. محاسبه مساحت مثلث بسیار آسان‌تر است. این فرایند را در انیمیشن زیر واضح‌تر می‌توانید مشاهده کنید:
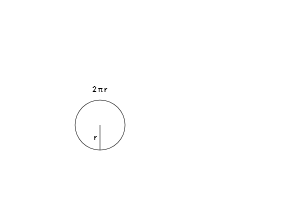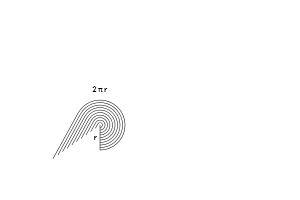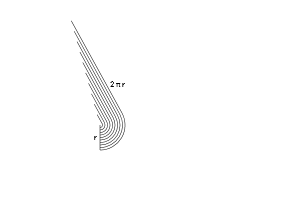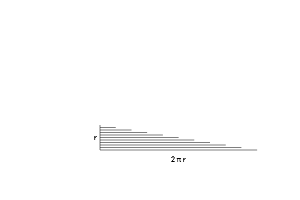
ارتفاع هر حلقه به مسافت اصلی آن از مرکز وابسته است. حلقه‌ای که 3 سانتی‌متر از مرکز فاصله دارد ارتفاعی برابر با 2π⋅3 سانتی‌متر خواهد داشت. کوچک‌ترین حلقه را می‌توان کمابیش یک نقطه منفرد تصور کرد که کلاً هیچ ارتفاعی ندارد. ارتفاع بزرگ‌ترین حلقه برابر با محیط دایره یعنی 2πr است.
از آنجا که محاسبه‌های مرتبط با مثلث آسان‌تر از دایره است، یافتن مساحت آن نیز کار دشواری محسوب نمی‌شود. فرمول مساحت مثلث به صورت نصف قاعده × ارتفاع است. بنابراین برای محاسبه مساحت مثلث، فرمول زیر را داریم:
$${1\over2}r(2πr)=πr^2$$
که همان فرمول محاسبه مساحت دایره است.
بینایی اشعه ایکس ما یک ساختار ساده و قابل اندازه‌گیری آسان را از یک شکل منحنی در اختیار ما قرار داد. ما درک کردیم که دایره و یک مجموعه از حلقه‌هایی که به هم چسبیده‌اند، در واقع یکسان هستند. از منظری دیگر یک دیسک تو پُر، همان تایم‌لپس از یک حلقه واحد است که بزرگ‌تر شده است.
با حسابان چه می‌توان کرد؟
در زمان یادگیری حساب آموختیم که چگونه اعداد را بشماریم و چگونه آن‌ها را با هم ترکیب کنیم (جمع/تفریق، ضرب/تقسیم، توان، جذر) از نظر فنی شمارش، ماهیتی ضروری ندارد، چون اجداد غارنشین ما بدون آن نیز موفق شده‌اند زنده بمانند.
اما داشتن نمادی برای کمیت موجب می‌شود که دنیا به مکانی آسان‌تر برای زندگی تبدیل شود. بدین ترتیب دیگر صرفاً دو کپه «بزرگ» و «کوچک» از سنگ نداریم، بلکه می‌توانیم آن‌ها را به تعداد دقیق بشماریم. بدین ترتیب آن‌ها می‌دانسته‌اند که چه تعداد تیر در اختیار هر شکارچی قرار داده‌اند و این که آیا میوه‌های چیده شده برای همه قبیله کافی هستند یا نه.
همچنین حساب، استعاره‌هایی در اختیار ما قرار می‌دهد که فراتر از محاسبات صرف است. حساب باعث می‌شود که توصیف‌های ما از همه چیز دقیق‌تر شوند، و بتوانیم برای همه چیز از سطح تندی غذا تا کیفیت فیلم (1 تا 5) و حتی حس و حال درونی‌مان (1 تا 10) با اعداد شاخص هایی تعریف کنیم. اندازه‌گیری دقیق، ایده مفیدی است و زمانی که با آن آشنا شدیم دیگر نمی‌توانیم آن را رها کنیم.
حسابان دو استعاره جدید به ما می‌آموزد و آن‌ها جدا کردن از هم و چسباندن در کنار هم هستند. یک الگو می‌تواند به بخش‌های مجزا تقسیم شود و این بخش‌ها می‌توانند به طور تدریجی در کنار هم قرار گیرند تا الگوی کامل دیگری را تشکیل دهند.
اگر بپرسید آیا این چشم‌انداز برای بقا ضروری است، پاسخ منفی است؛ اما بی‌شک جذاب است.
سخن پایانی
اعداد و معادلات آن چه را در اختیار داریم توصیف می‌کنند؛ اما حسابان مراحلی که برای رسیدن به آن موارد لازم هستند را نشان می‌دهد. بدین ترتیب به جای این که صرفاً کلوچه را ببینیم، می‌توانیم دستور آشپزی را ملاحظه کنیم.
بدیهی است که حسابان در همه زمینه‌های علمی مشاهده می‌شود، زیرا یک نقشه اولیه گام به گام، بسیار مفیدتر از رسیدن به نتیجه نهایی است. با این وجود ما در سناریوهای روزمره یک چشم‌انداز مناسب داریم که با طی چه مراحلی به این جا رسیده‌ایم و معمولاً مزایا و معایب مسیری که طی شده را بررسی می‌کنیم و بر اساس این مراحل در مورد مسیر آینده خود تصمیم‌گیری می‌کنیم. بخش دوم این نوشته را در با کلیک روی این لینک مطالعه بکنید.
اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزش‌های ریاضیات
- مجموعه آموزش های دروس دبیرستان و پیش دانشگاهی
- آموزش جامع ریاضی دبیرستان – ریاضی و فیزیک
- حد در بینهایت — به زبان ساده
- آموزش جامع حساب دیفرانسیل و انتگرال پیش دانشگاهی
==
