مفاهیم مقدماتی حسابان (بخش سوم) – به زبان ساده
در بخش قبلی این سری مقالههای «آشنایی با مفاهیم مقدماتی حسابان» در مورد راهبرد تفکر به روش «اشعه ایکس» و روش اعمال آن در محیط 2 بعدی صحبت کردیم. اینک این راهبرد بینایی اشعه ایکس خود را به محیط 3 بعدی نیز گسترش میدهیم. به تصاویر زیر دقت کنید.



بدین ترتیب
- حلقهها به پوستهها تبدیل میشوند. برای مثال آبنبات خوشمزهای را تصور کنید که پوسته رنگارنگی دارد.
- قاچها به گُوه تبدیل میشوند که قطاعهای یکسانی مانند قاچهای پرتقال هستند.
- برشها به صفحه تبدیل میشوند که دیسکهای ضخیمی هستند که میتوانند روی همدیگر انباشته شوند.
قطعههای 3 بعدی را میتوان این طور تصور کرد که گویی از همتایان 2 بعدی خود ساخته شدهاند. برای نمونه میتوانیم یک حلقه منفرد را مانند یک سکه بچرخانیم تا یک پوسته ایجاد شود. یک گوه مانند چند برش پیتزا (با اندازههای متفاوت) است که روی هم چیده شدهاند در نهایت اگر یک برش را حول محورش بچرخانیم یک صفحه به دست میآید.
مزایا و معایب هر کدام از این شکلهای 3 بعدی مانند همتایان 2 بعدیشان است.
- پردازشهای ارگانیک در لایههای پوسته به پوسته، رشد مییابند (مرواریدها درون صدف)
- تقسیمهای منصفانه به شکلهای گوه مانند نیاز دارند (ماند برش یک سیب برای دوستان مختلف)
- رویکرد صفحهای روباتیک برای تولید کارخانهای مناسب به نظر میرسد.
یک پرتقال ترکیب مناسبی از همه این موارد است. پرتقال از بیرون طوری به نظر میرسد، گویا از پوستههای مختلف ساخته شده است که در طی زمان رشد یافتهاند. اما از درون یک ساختار درونی متقارن به صورت گوه دارد که آن را برای توزیع متوازن مناسب میسازد. آن را میتوانیم به هر دو روش توصیف کنیم.
بسط منظر 3 بعدی
در بخش نخست این سری مقالات آشنایی با حسابان به اجمال بیان کردیم که فرمولهای دایره و کره با هم مرتبط هستند:
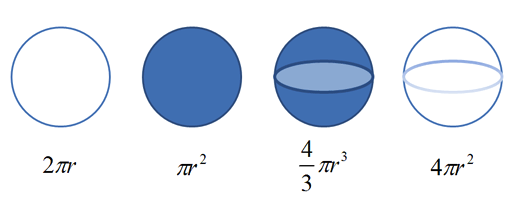
ما به کمک مهارتهای اشعه ایکس و تایم-لپس، ایدهای کلی از چگونگی این مسئله به دست میآوریم:
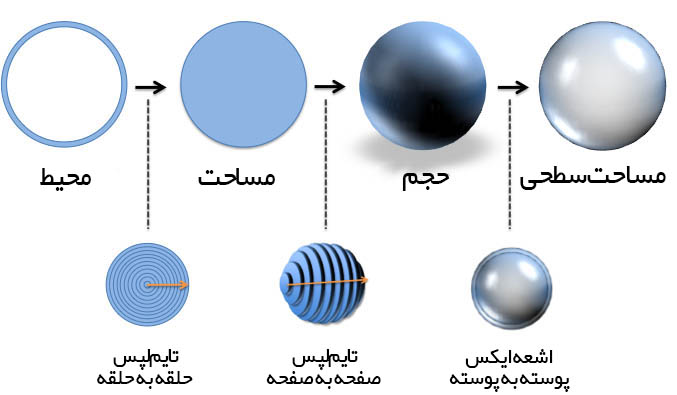
- محیط: با یک حلقه منفرد آغاز میشود.
- مساحت: با روش تایملپس حلقه به حلقه یک دیسک تو پر ایجاد میشود.
- حجم: یک دایره به یک صفحه تبدیل میشود و سپس با استفاده از رویکرد تایم-لپس صفحه به صفحه، یک کره ایجاد میشود.
- مساحت سطحی: اگر از رویکرد اشعه ایکس استفاده کنیم، میتوانیم آن را به یک دسته از پوستهها تقسیم کنیم. پوسته بیرونی همان مساحت سطحی است. ما اکنون توضیح دقیقی در مورد چگونگی ارتباط فرمولها با یکدیگر داریم. ما به طور شهودی می دانیم که چگونه با بهرهگیری از رویکردهای اشعه ایکس و تایملپس خود شکلها را به روشهای مختلف تغییر دهیم. ما حتی میتوانیم رو به عقب نیز عمل کنیم و با آغاز از یک کره و رویکرد اشعه ایکس آن را به صفحههایی تجزیه کنیم و سپس با انتخاب یک صفحه و بهکارگیری رویکرد اشعه ایکس آن را به حلقههایی تبدیل کنیم.
نیاز به نمادگذاری ریاضیاتی
احتمالاً متوجه شدهاید که با پیچیدهتر شدن موضوعات، توصیف ایدههای مختلف دشوارتر شده است. ما از قیاسهای فیزیکی (حلقه، برش، گوه) برای توصیف ایدههای خود استفاده میکنیم. برای نمونه بیان میکنیم: «این مساحت دایرهای را انتخاب میکنیم و دیسکهایی از روی آن میسازیم. سپس این دیسکها را کنار هم قرار میدهیم تا شکل یک کره ساخته شود.»
ما تا به اینجا سعی کردهایم مفاهیم مختلف را با استفاده از نمودار و قیاس توضیح دهیم؛ اما برای توصیف ایدههای خود نیازی به آنها نداریم.
اگر به روش توسعه یافتن اعداد دقت کنید، میبینید که در ابتدا از نمادهای بسیار ابتدایی برای شمارش به صورت I، II، III استفاده میشده است. در نهایت ما درک کردیم که نمادی مانند V میتواند به جای IIIII قرار گیرد و شاید حتی بهتر از آن، میتوانیم برای هر رقم نماد خاصی بسازیم. البته رقم 1 همچنان تاریخچه مبتنی بر کشیدن خط را برای شمارش یادآوری میکند. نمادگذاری ریاضیاتی به چند دلیل به ما کمک میکند:
نمادها کوتاهتر از کلمات هستند
حتماً موافق هستید که «5 = 3 + 2» بهتر از «دو به علاوه دو برابر با پنج» است. دقت کنید که علامت تساوی در سال 1557 از سوی «رابرت ریکورد» (Robert Recorde) به صورت دو خط موازی ابداع شده است زیرا این بهترین نماد برای نشان دادن برابری است.
استفاده از قواعد به انجام بهتر کارها کمک میکنند
هنگام استفاده از اعداد رومی در واقع ما اعداد را با استفاده از انگشتهای خود نشان میدهیم. چرا باید نوشتن VIII به انرژی بیشتری نسبت به I نیاز داشته باشد؟ این که 8 بزرگتر از 1 است دلیل خوبی برای این موضوع نیست. اعداد دهدهی به ما کمک میکنند که عمل نمایش اعداد را به راحتی انجام دهیم و دستکاری اعداد نیز آسانتر باشد. تا به این جا ما کار حسابان را به صورت دستی خودمان انجام دادهایم. یعنی دایره را به حلقههایی برش دادهایم، درک کردهایم که میتوانیم آن را باز کنیم، معادله مساحت را جستجو کردهایم و مثلث حاصل را اندازهگیری نمودهایم. در این موارد میتوانیم از قواعد استفاده کنیم. فقط کافی است آنها را به دست بیاوریم.
میتوانیم تفکر خود را تعمیم ببخشیم
«5 = 3 + 2» در وقع به معنی این است که «2 تا از هر چیزی + سه تا از هر چیزی = 5 تا از آن چیز» خواهد بود. با این که عجیب به نظر میرسد؛ اما ما در این جا یک کمیت انتزاعی داریم. در واقع عدد 2 با این که میتواند به انسان، پول، گاو یا هر چیز دیگری اشاره کند؛ اما هیچ کدام از آنها نیز نیست و مفهوم 2 تا را القا میکند. بدین ترتیب ما میتوانیم این عدد را به هر کمیتی نسبت دهیم. قواعد حساب چند منظوره هستند و نباید آنها را صرفاً به یک مورد خاص محدود کنیم.
نکته آخر بسیار حائز اهمیت است. زمانی که عمل جمع را یاد میگیریم، معمولاً از مثالهایی مانند سیب برای نمایش عمل جمع 2 به علاوه 3 استفاده میکنیم. با کمی تمرین میتوانیم شروع به استفاده از نمادهای مجرد بدون نیاز به نمونههای فیزیکی بکنیم و معنی «5 = 3 + 2» را درک میکنیم.
حسابان نیز مشابه جمع است. در حسابان معادلههای انتزاعی مانند وجود دارد؛ اما نمونههای فیزیکی نقطه شروع خوبی هستند. وقتی شکلی مانند زیر میبینیم:

بدین ترتیب میتوانیم در عمل درک کنیم که وقتی از یک تکنیک خاص استفاده میکنیم، حسابان چه کاری برای ما انجام میدهد و صرفاً به بازی با نمادها نمیپردازیم. در نهایت باید گفت که میتوان شکلهای مختلف را به معادلهای متناظر تبدیل کرده و به صورت مستقیم با نمادها کار کرد.
بنابراین همان طور که برای جمع زدن به سیب نیاز نداریم؛ حسابان نیز برای کارکرد خود به اشیایی در دنیای فیزیکی نیاز ندارد. ما با استفاده از حسابان میتوانیم هر شکل یا فرمولی مانند معادله فیزیک، سناریوی تجاری، نمودار یک تابع را تحلیل کنیم. شکلهای مختلف صرفاً برای شروع و آشنایی مفید هستند.
برای مشاهده بخش بعدی این مطلب میتوانید از لینک زیر استفاده کنید:
اگر این نوشته برای شما مفید بوده است، پیشنهاد ما استفاده از آموزشهای زیر است:
- مجموعه آموزشهای ریاضیات
- آموزش جامع ریاضی دبیرستان
- مجموعه آموزشهای دروس رسمی دبیرستان و پیش دانشگاهی
- تقلب نامه (Cheat Sheet) مفاهیم و روابط حد و پیوستگی
- آموزش جامع حساب دیفرانسیل و انتگرال پیش دانشگاهی
- حد در بینهایت — به زبان ساده
==












