نمودار جعبه ای (Boxplot) و رسم آن در پایتون – به زبان ساده
یکی از معروفترین نمودارها که بسیاری از شاخصهای آمار توصیفی مربوط به دادهها را نشان میدهد، «نمودار جعبهای» (Boxplot) است. این نمودار توسط آمارشناس مشهور آمریکایی «جان توکی» (John Wilder Tukey) در سال 1969 معرفی شد. در این متن به بررسی این نمودار میپردازیم و با شیوه ترسیم آن را در زبان برنامه نویسی پایتون آشنا میشویم. ذکر این نکته نیز ضروری است که گاهی به نمودار جعبهای، «نمودار جعبه و خط» (Box and Whisker) نیز میگویند. برای درک بهتر این نوشتار بهتر است ابتدا مطالب مربوط به شاخصهای آماری تمرکز و پراکندگی را مطالعه کرده باشید. البته مطالعه نوشتار نمایش و رسم نمودار برای دادهها — معرفی و کاربردها خالی از لطف نیست.


نمودار جعبهای
تصویر زیر بیانگر یک نمودار جعبهای است. همانطور که در ادامه دیده خواهد شد برای رسم این نمودار از چندین شاخص مرکزی و پراکندگی آماری استفاده شده است. کدهای رسم نمودار با کد رسم شکل در پایتون تفاوت دارد.
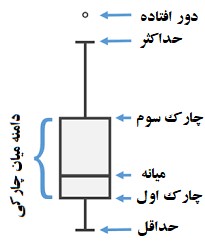
نمودار جعبهای یک روش استاندارد برای نمایش توزیع دادهها است که براساس شاخصهای آماری «کوچکترین مقدار» (Minimum)، «چارک اول» (First Quartile -Q1)، «میانه» (Median)، «چارک سوم» (Third Quartile- Q3) و «بزرگترین مقدار» (Maximum) ساخته شده است. همچنین این نمودار میتواند در مورد وجود دادههای دورافتاده (Outlier) یا پرت، اطلاعاتی به شما بدهد و مقدار آنها را تعیین کند. همچنین نشان دادن تقارن در دادهها از کارهایی این نمودار است. شایان ذکر است که میزان تمرکز و حتی چولگی دادهها نیز در این نمودار دیده میشود. در این نوشتار به مطالب زیر اشاره خواهد داشت:
- نمودار جعبهای چیست؟
- ساختار و اجزای یک نمودار جعبهای و ارتباط آن با منحنی توزیع نرمال
- ایجاد و ترسیم نمودارهای جعبهای بوسیله زبان برنامه نویسی پایتون
نمودار جعبهای چیست؟
به نظر میرسد تکیه کردن به شاخصهای تمرکز مانند میانگین، میانه و نما به تنهایی کافی نیست. فرض کنید قرار است که کارایی team1 و team2 با یکدیگر مقایسه شود. شاخصهای تمرکز برای این کار استفاده و مقدارشان برای هر دو تیم محاسبه شده است.
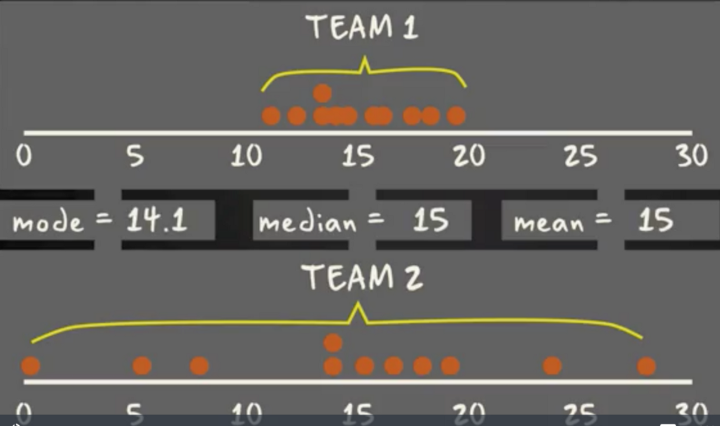
همانطور که در تصویر بالا دیده میشود، برای مقایسه دو تیم فقط از معیارهای تمرکز استفاده شده است. نتیجه بسیار عجیب است! اگر چه معیارهای تمرکز برای تیم ا و ۲ با هم برابر است ولی به وضوح دیده میشود که تیم ۱ یکدستتر از تیم ۲ است. به همین علت استفاده از معیارهای پراکندگی و تمرکز همزمان ضروری به نظر میرسد. نمودار جعبهای از عهده این کار یعنی نمایش معیارهای تمرکز و پراکندگی همزمان به خوبی برمیآید. البته برای چنین کاری میتوان از «نمودار توزیع فراوانی» (Histogram) یا «نمودار احتمال- چگالی» (Probability-Density Plot) نیز کمک گرفت. ولی از طرفی استفاده از نمودار جعبهای برتریهایی نیز نسبت به رسم «نمودار چگالی» (Density Plot) و «بافتنگار» (Histogram) دارد زیرا فضای کمتری اشغال میکند در نتیجه امکان مقایسه بین چند گروه مختلف را همزمان میدهد. این گونه نمودارهای جعبهای که به منظور مقایسه بین چندین گروه ترسیم میشوند را در ادامه خواهید دید. در تصویر زیر یک نمونه از نمودار جعبهای مشاهده میشود. همانطور که قابل مشاهده است، اجزای این نمودار در ترسیم آن نقش مهمی دارند. بنابراین بهتر است با این قسمتها بیشتر آشنا شویم.
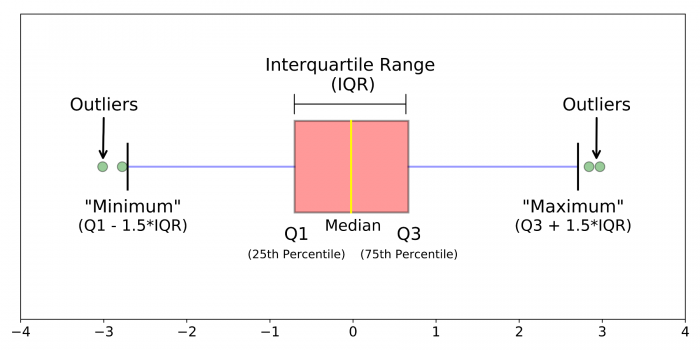
میانه (Median): این شاخص آماری مقداری را نشان میدهد که در وسط دادهها قرار دارد. این محل در نمودار بوسیله خطی زرد رنگ به نام Median دیده میشود. مشخص است که ۵۰٪ دادهها از این مقدار کوچکتر یا بزرگتر هستند. این شاخص توسط یک خط عمودی درون جعبه ترسیم میشود.
چارک اول (Q1): این شاخص، مقداری را نشان میدهد که ۲۵٪ دادهها از آن کوچکتر هستند. از طرفی میتوان این مقدار را میانه دادههایی دانست که بین کوچکترین مقدار (با توجه به دادههای پرت) و میانه قرار گرفتهاند. این مقدار توسط یک خطی عمودی بدنه سمت چپ جعبه را میسازد.
چارک سوم (Q3): این شاخص، مقداری را نشان میدهد که ۷۵٪ دادهها از آن کوچکتر هستند. از طرفی میتوان این مقدار را میانه دادههایی داسنت که بین بزرگترین مقدار (با توجه به دادههای پرت) و میانه قرار گرفتهاند. این شاخص نیز برای نمایش ضلع سمت راست جعبه به کار گرفته میشود.
دامنه میان چارکی (IQR): فاصله بین چارک اول و سوم توسط این شاخص نشان داده میشود. طول اضلاع دیگر جعبه توسط این شاخص تعیین میشود.
خطوط (Whikers): این خطوط فاصله بین چارک اول تا کمترین مقدار و همچنین بیشترین مقدار را پر میکنند. در تصویر بالا این خطوط به رنگ آبی نشان داده شدهاند.
حداکثر- بزرگترین مقدار (Maximum): در این نمودار بزرگترین مقدار، بیشترین مقداری است که حداکثر 1.5 برابر دامنه میان چارکی از چارک سوم فاصله دارد. به بیان ریاضی میتوان نوشت:
حداقل- کوچکترین مقدار (Minimum): در این نمودار کوچکترین مقدار، کمترین مقداری است که حداکثر 1.5 برابر دامنه میان چارکی از چارک اول فاصله دارد. به بیان ریاضی میتوان نوشت:
دادههای دورافتاده- پرت (Outlier): مقدارهایی که به شکل دایره سبز رنگ در نمودار مشاهده میشوند، دادههایی پرت هستند. در اینجا دادههایی که از Minimum کوچکتر و یا از Maximum بزرگتر هستند، داده پرت محسوب میشوند.
مقایسه نمودار جعبهای با منحنی احتمال نرمال
در تصویر زیر مقایسه بین منحنی «چگالی احتمال» (Probability Density) نرمال و نمودار جعبهای صورت گرفته است. این کار برای درک بهتر از نمودار جعبهای و نشان دادن خصوصیات آن ضروری به نظر میرسد. به این ترتیب خواهید فهمید که مزیتهای یک نمودار جعبهای در مقایسه با نمودار احتمال در چیست! همچنین، این مقایسه به درک شاخصهای کوچکترین و بزرگترین مقدار و همچنین دادههای پرت کمک خواهد کرد.

همانطور که در مطالب فرادرس با عنوان توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها گفته شده است، تابع چگالی احتمال ، جرم احتمال در هر نقطه از اعداد حقیقی مثلا (x) را نشان میدهد.
شکل تابع چگالی برای توزیع نرمال به صورت زیر نوشته میشود:
ولی در اینجا برای سادگی بیشتر، پارامتر میانگین () را صفر و واریانس () را مقدار ۱ در نظر میگیریم. در نتیجه تابع چگالی برای توزیع نرمال استاندارد حاصل میشود که به صورت زیر خواهد بود:
برای رسم نمودار چگالی این توزیع از زبان برنامه نویسی پایتون استفاده کردهایم. کدهای زیر ترسیم این منحنی را برایمان انجام میدهند.
با اجرای این برنامه نموداری مانند تصویر زیر ساخته میشود.
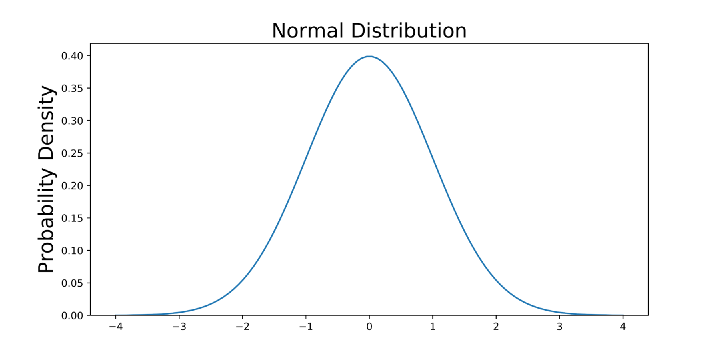
هرچند این نمودار، میزان احتمال را برای هر پیشامد نشان نمیدهد ولی جرم احتمال برای هر نقطه دیده میشود. از آنجایی که احتمال برای تک نقطهایها در توزیعهای پیوسته صفر است، احتمال برای محدودهای از مقادیر توسط انتگرالگیری و محاسبه سطح زیر این منحنی در آن محدوده قابل محاسبه است.
برای مثال فرض کنید که میخواهیم مقدار احتمال را برای قرارگیری یک عدد تصادفی از توزیع نرمال در فاصله IQR (یعنی به اندازه 0.6745 انحراف استاندارد بیشتر از میانگین و 0.6745 انحراف استاندارد کمتر از میانگین) محاسبه کنیم. البته برای این کار جدولهایی نیز تهیه شده است ولی برای محاسبه دقیقتر میتوان از نرمافزارهای محاسباتی مانند پایتون استفاده کرد.
کد زیر برای انجام این محاسبه نوشته شده است که نتیجه انتگرال زیر است.
شاید سوال کنید چرا باید انتگرال را در محدود 0.6745- تا 0.6745 محاسبه کرد! اگر فرض کنیم که توزیع نرمال استاندارد مورد نظرمان است، میانگین برابر با صفر و واریانس نیز برابر با ۱ است. از آنجایی که باید انتگرال از چارک اول تا چارک سوم محاسبه شود، باید نقاطی را از دادههای توزیع نرمال استاندارد در نظر بگیریم که احتمال تا آنها برابر با ۲۵٪ و ۷۵٪ باشد. طبق جدول توزیع نرمال استاندارد مقدار حدودی برای این نقاط 0.6745- و 0.6745+ است.
همانطور که در تصویر زیر دیده میشود، این مقدار برابر با 0.5 یا همان ۵۰٪ است.
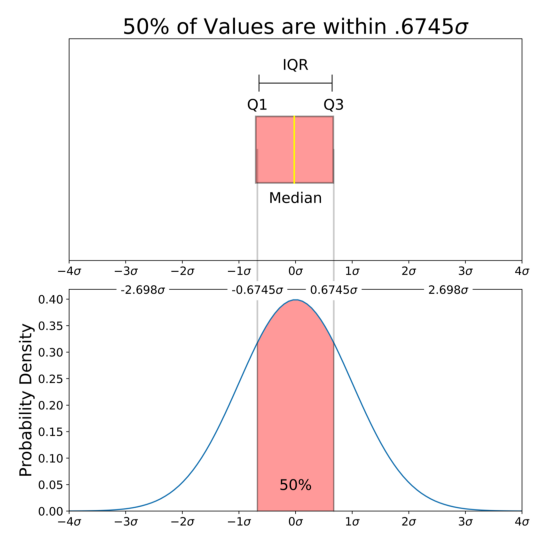
همین کار را هم برای بزرگترین و کوچکترین مقدار تکرار میکنیم. کدهای پایتون که در ادامه دیده میشود، انتگرال زیر را محاسبه میکند.
توجه داشته باشید که مقدار 2.698- و 2.698+ به همان دلیل قبلی انتخاب شدهاند. یعنی برای کران بالای انتگرال، نقطهای در نظر گرفته شده است که فاصلهاش از چارک سوم 1.5 برابر دامنه میان چارکی باشد. همچنین برای کران پایین انتگرال نیز نقطهای منظور شده است که از چارک اول به اندازه 1.5 برابر دامنه میان چارکی فاصله دارد. نتیجه کار طبق نمودار زیر ترسیم شده است. مشخص است که این احتمال برابر با 99.3٪ است.
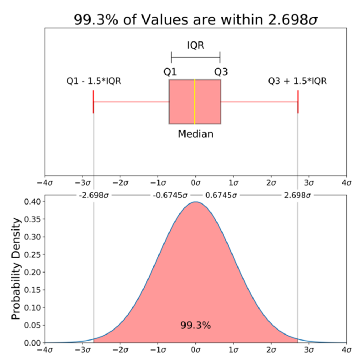
کار بر اساس دادههای واقعی
از آنجایی که همیشه دادهها، توزیع نرمال ندارند، میخواهیم براساس دادههای واقعی عمل کنیم. این دادههای مربوط به اطلاعات و ارقام واقعی مربوط به سرطان سینه از یک بانک اطلاعاتی است. کدهای پایتون که در زیر دیده میشود، اطلاعات مربوط به بانک اطلاعاتی سرطان سینه را از اینترنت دریافت و وارد متغیر df میکنند.
رسم نمودار جعبهای
در اینجا منظور از رسم نمودار جعبهای نمایش رابطه بین متغیر طبقهای (X) و متغیر پیوسته (Y) است. متغیر X با برچسب (Diagnosis) دارای دو نوع مقدار «خوشخیم» (Benign) و «بدخیم» (Malignant) است که نوع تومر را نشان میدهد و Y نیز با برچسب (area_mean)، میانگین اندازه تومر را بیان میکند.
با استفاده از سه روش میتوانید نمودار جعبهای را در پایتون ترسیم کنید. در ادامه به بررسی کدهایی میپردازیم که نمودار جعبهای را به سه روش متفاوت ترسیم میکنند.
استفاده از seaborn و pandas
کد زیر دادههای ثبت شده در df که توسط pandas جمعآوری شدهاند، را برای ترسیم نمودار جعبهای به seaborn میفرستد. این دو کتابخانه از معروفترین کتابخانههای پایتون هستند.
با اجرای این کد، خروجی به صورت زیر در خواهد آمد. همانطور که دیده میشود بین سطح اشغال شده توسط تومر بدخیم که با کد M نشان داده شده و خوشخیم که با کد B دیده میشود، تفاوت فاحشی وجود دارد.
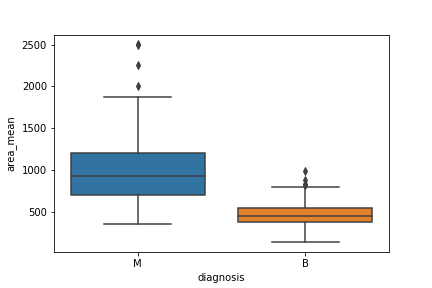
نکته: توجه داشته باشید که در اینجا نمودار جعبهای به صورت عمودی ترسیم شده است تا مقایسه بین گروهها بهتر انجام شود.
استفاده از matplotlib
ترسیم نمودار جعبهای با استفاده از کتابخانه matplotlib کمی پیچیده است ولی در عوض کنترلهای بیشتری برای ترسیم نمودار در اختیارتان قرار میگیرد. کدهای زیر به این منظور تهیه شدهاند.
خروجی برای این برنامه در شکل زیر دیده میشود. همانطور که دیده میشود برای هر مقدار از متغیر طبقهای diagnosis یک نمودار جعبهای ترسیم شده است. همچنین دستوراتی برای تنظیم محتویات مربوط به محور افقی نیز وجود دارد.
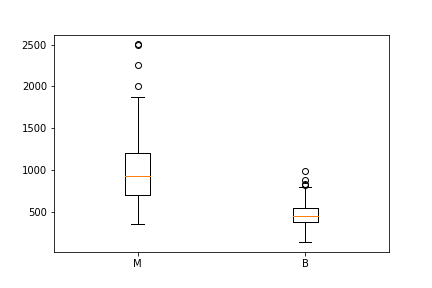
استفاده از pandas
با فراخوانی تابع روی منبع اطلاعاتی df میتوانید نمودار جعبهای را در pandas ترسیم کنید. کد زیر براساس متغیر area_mean جعبههایی به تفکیک متغیر diagnosis ترسیم میکند.
خروجی این دستور، ترسیم نموداری است که در زیر تصویر آن را میبینید. مشخص است که ترتیب قرارگیری جعبهها براساس حروف الفبا صورت گرفته است.
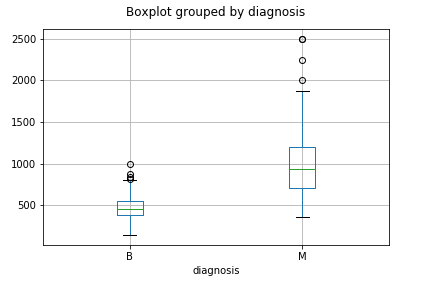
نکته: حتما به یاد دارید که دایرههایی که بالا یا پایین خطوط بزرگترین و کوچکترین مقدار قرار گرفتهاند، نشاندهنده نقاط پرت هستند.
رسم نمودار جعبهای با فاصله اطمینان برای میانه
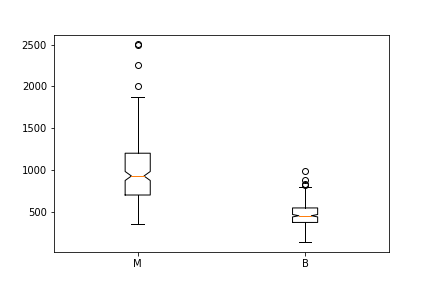
به کمک دستورات زیر میتوانید یک نمودار جعبهای ترسیم کنید که به همراه فاصله اطمینان 95٪ برای میانه باشد. به چنین نموداری اصطلاحا نمودار «جعبهای بریدهشده» (Notched Boxplot) میگویند.
قسمت بریده شده در این نمودار ناحیه فاصله اطمینان برای میانه را نشان میدهد. کد زیر برای ترسیم چنین نموداری مناسب است.
نتیجه اجرای این کدها، نمودار جعبهای بریدهشدهای است که به تفکیک نوع تشخیص تومر ترسیم شده.
تفسیر نمودار جعبهای
ابتدا اجازه دهید تا نمودار قبلی را به شکل زیباتری نمایش دهیم تا بتوانیم بهتر آن را تفسیر کنیم. کدهای زیر به این منظور تهیه شدهاند.
با اجرای این برنامه نموداری به مانند زیر ایجاد خواهد شد.
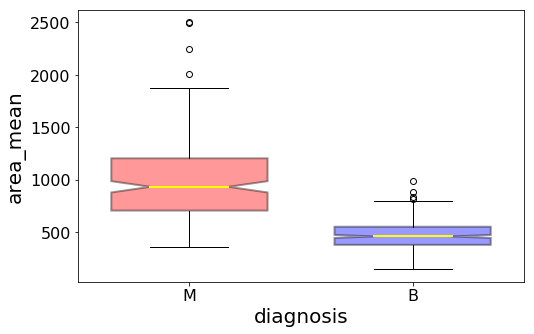
با استفاده از این نمودار میتوان اطلاعات زیر را به دست آورد:
میانه و محل جعبه: دامنه تغییرات ناحیه سرطان را بین دو نوع تومر قابل مقایسه است. کاملا مشخص است که تومرهای بدخیم ناحیه گستردهتر و بزرگتری دارند زیرا قسمت جعبه آنها بالاتر از تومرهای خوشخیم قرار گرفته است.
دامنه میان چارکی یا ارتفاع جعبه: پراکندگی میانگین سطح سرطانی نیز برای تومرهای بدخیم بیشتر از تومرهای خوشخیم است، زیرا ارتفاع جعبه تومرهای این گروه بزرگتر از ارتفاع جعبه تومرهای خوشخیم است.
دادههای پرت: هرچند برای هر میانگین سطح سرطانی دو نوع تومر، سه داده پرت شناسایی شده است ولی به نظر میرسد که برای تومرهای بدخیم دادههای پرت خیلی بزرگتر از اکثر دادهها هستند.
فاصله اطمینان میانه: از آنجایی که ناحیه مربوط به فاصله اطمینان میانگین سطح تومرهای بدخیم هیچ ناحیه مشترکی با فاصله اطمینان میانگین سطح تومرهای خوشخیم ندارد، به نظر میرسد که می توان با ۹۵٪ اطمینان گفت که میانههای سطح این دو نوع تومر از لحاظ آماری با یکدیگر اختلاف معنیداری دارند. با این کار یک آزمون آماری دوطرفه در سطح خطای ۵٪ برای میانههای سطح تومر در بین دو جامعه انجام دادهایم.
جمعبندی و نتیجهگیری
توجه داشته باشید که همیشه نمودار جعبهای براساس دادههای جمعآوری شده و مقدار متغیرهای مشاهده شده رسم میشود. در نتیجه برای مشخص کردن نوع توزیع دادهها نمیتوان از نمودار جعبهای کمک گرفت. وجود تقارن، سنجش شاخصهای پراکندگی و مرکزی ممکن است در شناخت توزیع دادهها به شما کمک کند ولی توزیع دقیق دادهها را به دست نمیدهد.
باید توجه داشت که هنگام مقایسه نمودارهای جعبهای برای دادههایی که به گروه یا دستههای مختلف تقسیم بندی شدهاند، از یک محور عمودی استفاده شود. به این معنی که متغیر کمی برای مقایسه در این نمودار باید برای همه گروهها دارای واحد اندازهگیری یکسانی باشد. اگر دامنه تغییرات یکی از گروهها بسیار زیاد باشد، ممکن است نمودار نتواند اطلاعات مربوط به گروههای دیگر را به خوبی نشان دهد. بهتر است برای جلوگیری از این امر، دادهها را هنگام استفاده در نمودار جعبهای استاندارد کنیم. این کار در مطلب فرادرس با عنوان روشهای استاندارد سازی دادهها قابل مطالعه است.












با سلام
مطالب نسبتا مفیدی برای منی که به تازگی دارم سعی می کنم اطلاعات آماری ام را برای یادگیری ماشین و نمودارهای آن بالا ببرم، بود. سپاس گذارم.
سلام
منظورتون از داده سرطیانی در قسمت داده ها پرت قبل از جمع بندي چي هست
مطالب ارائه شده خوب بود ولي به نطرم يه مقدار خيلي کمي کدهارو توضيح ميدادي خيلي خوب بود