معادله برنولی – به زبان ساده
هنگامی که سیالی در یک کانال با سطح مقطعی باریک جریان مییابد، سرعت آن زیاد میشود. این اتفاق به معنی افزایش انرژی جنبشی سیال است. به راستی این افزایش انرژی از کدام منبع ناشی میشود؟ این ازدیاد انرژی جنبشی، بهدلیل کار انجام شده روی سیال و همچنین وجود نیروی گرانش است. بنابراین با توجه به معادله کار-انرژی میتوان نوشت:


Wnet = 1/2mv2 − 1/2mv02
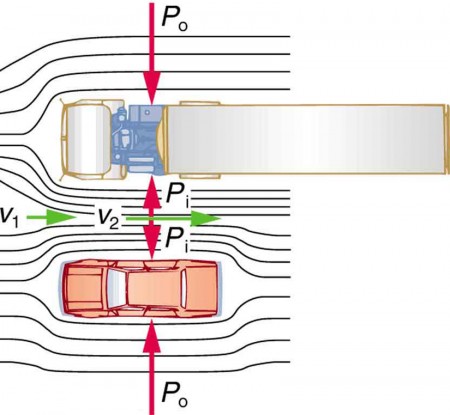
در فرآیند عبور جریان از کانال، ممکن است سطح مقطع کانال متغیر باشد. در چنین حالتی، تغییر سطح، منجر به ایجاد اختلاف فشار در کانال شده که نهایتا نیرویی را به سیستم وارد میکند. مثالهای زیادی در مورد افت فشار وجود دارد. شاید تابحال تجربه کرده باشید، هنگامی که در اتوبان رانندگی میکنید و ناگهان کامیونی از کنار شما عبور میکند، احساس میکنید که اتومبیل شما به سمت کامیون کشیده میشود. دلیل این امر وجود ناحیه کمفشار بین کامیون و خودروی شما است. خوب است بدانید که این معادله مبنای مکانیک سیالات محسوب میشود.
معادله برنولی
رابطه کمی بین سرعت و فشار برای اولین بار با استفاده از فرمول برنولی بیان شد. این معادله بیان میکند که برای یک جریان بدون اصطکاک و غیر تراکمپذیر، حاصل جمع عبارت زیر همواره ثابت میماند.
P + 1/2ρv2 + ρgh = ثابت
در این معادله P ،v ،ρ ،h و g بهترتیب برابر با ارتفاع، چگالی، سرعت، فشار و شتاب گرانشی هستند. اگر حجم اندکی از سیال در طول مسیرش دنبال شود، هر کدام از اجزای سمت چپ معادله بالا ممکن است تغییر کند، اما مجموع این مقادیر، ثابت خواهند ماند. بنابراین با فرض اینکه 1 و 2، دو نقطه از سیال باشند که روی یک مسیر قرار گرفتهاند، میتوان نوشت:
P1 + 1/2ρv12 + ρgh1 = P2 + 1/2ρv22 + ρgh2
اگر دقت کنید، این معادله شکل جدیدی از قانون پایستگی انرژی را مطرح میکند. توجه داشته باشید که عبارت دوم و سوم، همان انرژی جنبشی و پتانسیل هستند که در آنها چگالی به جای جرم قرار گرفته. در واقع واحد هر کدام از این عبارات، انرژی بر حجم سیال است. به عنوان مثال برای انرژی جنبشی میتوان نوشت:
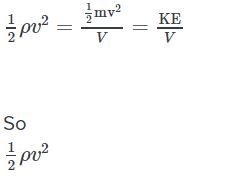
اگر دقت کنید معادله بالا همان انرژی جنبشی بر واحد حجم است.
معادله برنولی برای سیال ساکن
حالتی را فرض کنید که در آن سیال در نقطه 1 و 2 بهصورت ساکن قرار گرفته. در این حالت معادله برنولی را میتوان بهشکل زیر بیان کرد.
P1 + ρgh1 = P2 + ρgh2
میتوان با فرض h2=0 معادله مفروض را سادهتر کرد. بنابراین معادله برنولی بهصورت زیر قابل بازنویسی است.
P2 = P1 + ρgh1
این معادله به ما میگوید که در یک سیال ساکن، فشار با افزایش عمق، زیاد خواهد شد. در واقع زمانی که در یک سیال از نقطه 1 به 2 برویم، عمق سیال مد نظر به اندازه h1 افزایش خواهد یافت؛ بنابراین فشار نقطه 2 از فشار نقطه 1 به اندازه ρgh1 بیشتر خواهد بود. رابطه معروف P=ρgh در استاتیک سیالات نیز از همین مفهوم ناشی شده.
معادله برنولی در مورد سیال ساکن، این مفهوم ساده را بیان میکند که فشار ناشی از جرم مشخصی از سیال، برابر با وزن آن تقسیم بر سطح مقطع است.
معادله برنولی در عمق ثابت
حالت دیگری از این معادله، هنگامی است که سیال در یک عمق ثابت حرکت میکند. در این موارد فرض h1=h2 درست است. تحت چنین شرایطی، رابطه برنولی به شکل زیر نوشته میشود.
P1 + 1/2ρv12 = P2 + 1/2ρv22
به چنین شرایطی که سیال در مسیری جریان مییابد که عمق آن تغییر نمیکند، قانون برنولی گفته میشود. در حقیقت قانون برنولی همان معادله برنولی، ولی در شرایطی است که عمق تغییر نکند. از این معادله نتیجه گرفته میشود که با افزایش سرعت سیال در یک عمق ثابت، فشار آن کاهش خواهد یافت. در واقع این فرآیند، همان تبدیل شدن انرژی پتانسیل به انرژی جنبشی است.
مثال
سرعت جریانی در یک کانال (کانال کاملا بهصورت افقی قرار گرفته است) از 1.96 تا 25.5 متر بر ثانیه (سطح مقطع کانال متغیر است) افزایش مییابد. اگر فشار سیال در سرعت 25.5 برابر با 100,000 نیوتن بر متر مربع باشد، فشار در نقطه اول (نقطهای که سرعت آن 1.96 بوده) چقدر است؟
از آنجایی که ارتفاع این کانال تغییر نمیکند، معادله برنولی را میتوان بهصورت زیر بیان کرد.
(P1 + 1/2ρv12 = P2 + 1/2ρv22 = P2 + 1/2ρ(v22 − v12
نقطه اول جایی است که سرعت سیال کمتر محسوب میشود. با جایگذاری مقادیر سرعت و چگالی در این معادله، فشار در نقطه اول بهشکل زیر محاسبه میشود.
[P1 = 71.01×105 N/m2 + 1/2(103 kg/m3)[(25.5 m/s)2 − (1.96 m/s)2
=4.24×105 N/m2
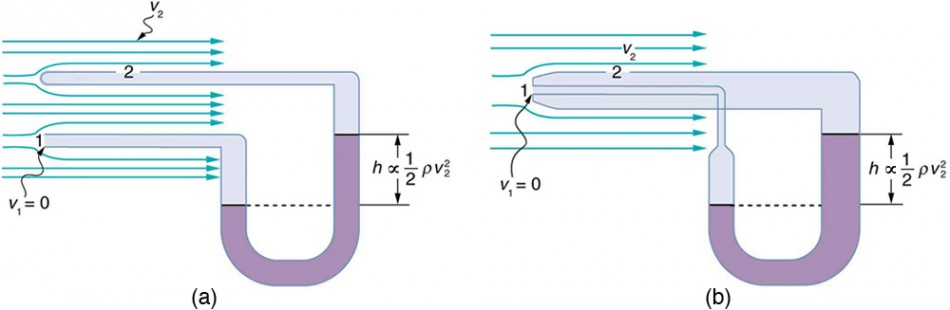
کاربرد معادله برنولی در اندازهگیری سرعت
شکل زیر دو وسیله را نشان میدهد که سرعت سیال را بر اساس معادله برنولی اندازهگیری میکنند. مانومتر که نوعی وسیله اندازهگیری فشار محسوب میشود، به دو لوله متصل شده که به منظور جلوگیری از منحرف کردن جریان، به اندازه کافی کوچک طراحی شدهاند. سرعت جریانی که به سمت جسم میآید، در نقطه خاصی به صفر میرسد. این مکان را «نقطه سکون» (Stagnation Point) مینامند. به دلیل کاهش سرعت سیال، فشار آن نیز افزایش خواهد یافت. این همان مکانیزمی است که در وسایل حمل و نقل هوایی از آن استفاده میشود. در این حالت معادله برنولی بهشکل زیر نوشته میشود.
P1 = P2 + 1/2ρv22
این تغییر فشار، معادل با افزایش ارتفاع h است که در لوله رخ میدهد. بنابراین میتوان بیان کرد.
v2∝√h
شکل زیر شماتیک ابزاری را نشان میدهد که معمولا در هواپیماها به منظور اندازهگیری سرعت، از آن استفاده میشود.
توان در جریان سیال
نرخ انجام کار و یا انتقال انرژی به یک سیستم، توان نامیده میشود. بهمنظور بررسی توان ورودی و یا خروجی از سیال، معادله برنولی را در قالب زیر در نظر بگیرید.
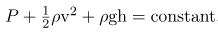
همانطور که در بالا نیز بیان شد، بُعد تمامی این عبارتها، انرژی بر واحد حجم است. حال تمامی این عبارتها را به شکل زیر در نرخ جریانِ Q ضرب کنید.
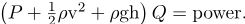
تمامی این عبارتها دارای معنای مشخص هستند. برای نمونه، PQ توانی است که مثلا پمپ به سیال میدهد. همچنین عبارت ۱/۲ρv2Q به معنای توانی است که انرژی جنبشی سیال را افزایش میدهد.
در صورتی که به مباحث مرتبط در زمینه مکانیک سیالات علاقهمند هستید، احتمالا آموزشهای زیر میتوانند برایتان مفید باشند:
- مجموعه آموزشهای دروس مهندسی مکانیک
- مجموعه آموزشهای فنی و مهندسی
- استاتیک سیالات - به زبان ساده
- سینماتیک سیالات - مقدمهای بر مکانیک
- ترمودینامیک - از صفر تا صد
^^













سلام. اگه مخزنی به حجم ۴ متر مکعب هوا با فشار ۷ بار داشته باشیم دبی خروجی هوا از این مخزن چقدر میشه؟ سایز لوله خروجی یک اینچ است.
با سلام خدمت شما؛
پاسخ سوال با در نظر گرفتن این نکات که مخزن تحت فشار مطلق ۸ بار هست (یعنی ۷ بار فشار گیج)، خروجی لوله آزاد تحت فشار جو (یعنی ۱ بار فشار مطلق) قرار دارد، دمای هوا ۲۰ درجه سانتیگراد است و اینکه تخلیه به شکل ناگهانی نیست، بلکه بهصورت پایدار انجام میشود، با استفاده از «دبی ماکزیمم چوک» (چاکد فلو یا Choked Flow) تخمین زده میشود. در این روش در جریان گاز از لوله به محیط با فشار بسیار کمتر، اگر اختلاف فشار زیاد باشد (برای مثال ۸ بار → ۱ بار)، جریان به حالت «چوک» میرسد و ماکزیمم دبی ممکن از آن لوله عبور میکند.
از همراهی شما با مجله فرادرس سپاسگزاریم.
مجید جان دستت درد نکنه برادر مطالبت خیلی کمکم کرده
فیلماتون یه جوریه ادم بدتر قاطی میکنه
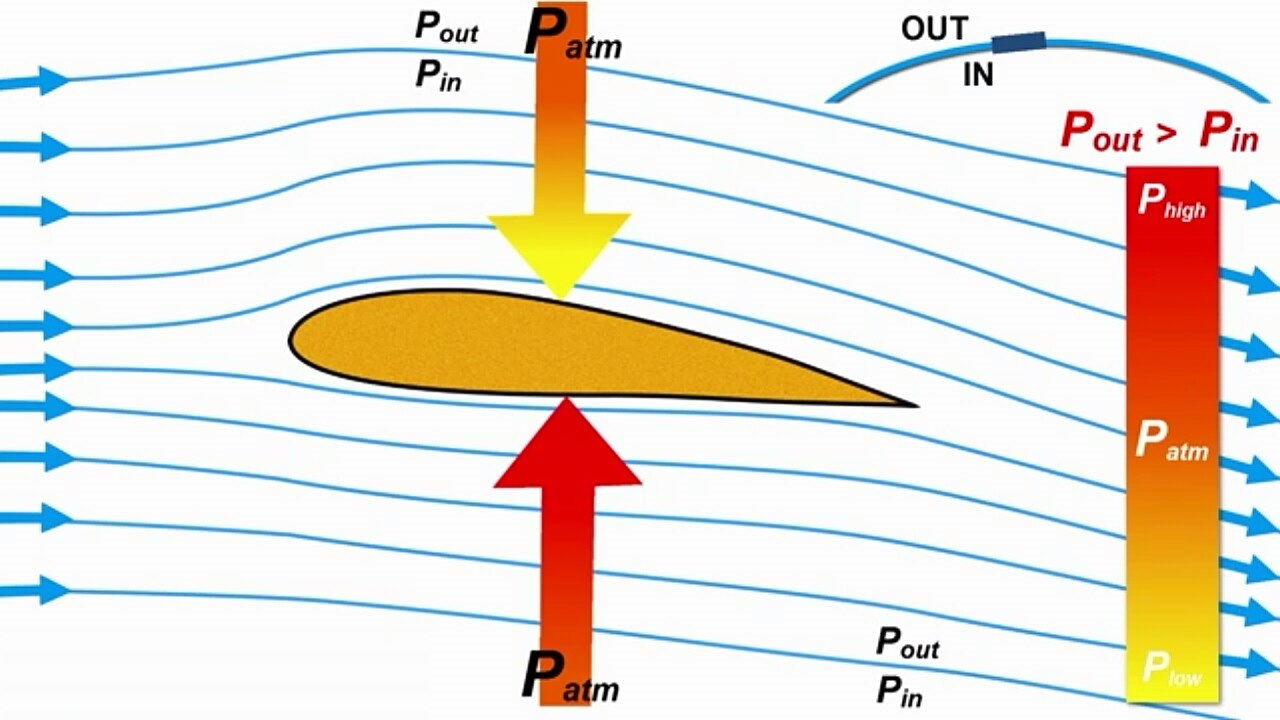
اگر معدله برنولی تنها برای سیالات تراکم ناپذیر صادق است پس چرا در مثالهای شما از سیالات قابل تراکم استفاده شده است مثل مثال ایرفویل یا عبور یک کامیون و سواری از کنار یکدیگر؟
از نظر من مطلب رو ساده و شیوا و با تدریسی کاربردی ارائه دادین که فهم مطالب مطرح شده در دبیرستان رو ، ساده تر میکنه .
از لطف شما برای تهیه این مطلب تشکر و از زحمتتون برای آماده کردن این مطلب قدردانی میکنم.
بسیارخوب