تقارن محوری در اشکال دوبعدی – به زبان ساده
در این آموزش میخواهیم در خصوص تقارن محوری در اشکال دو بعدی صحبت کنیم.


بهتر است این مبحث را با یک مثال ساده شروع کنیم. به تصویر زیر توجه کنید. در این تصویر تنها نیمه چپ عکسبرداری شده است و به کمک کمی ویرایش، تصویر متقارن آن در سمت راست ایجادگردیده است. به این نوع از تقارن، تقارن محوری (گاهی اوقات تقارن انعکاسی یا تقارن آینه ای نامیده می شود) و به خط سفیدی که از بالا به پایین کشیده شده است و تصویر نسبت به آن تقارن دارد، محور تقارن گفته می شود.

انعکاس تصویر کوه در این دریاچه نیز دارای تقارن است. در این عکس محور تقارن از سمت چپ به راست کشیده شده است. تصویر قله دارای تقارن کامل نیست؛ زیرا پس از انعکاس در سطح دریاچه کمی تغییر کرده است.

محور تقارن
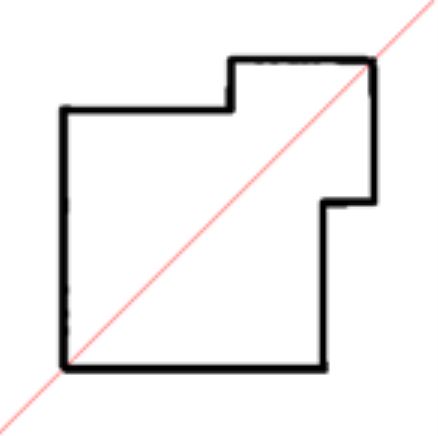
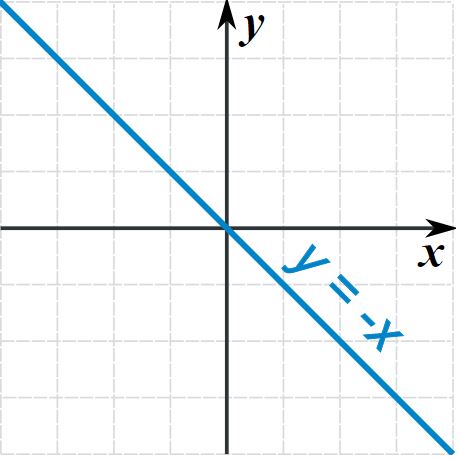
محور تقارن (که محور آینه ای هم نامیده می شود) میتواند در هر جهتی باشد. اما به طور کلی 4 جهت رایج برای اینگونه محورها وجود دارد. در جدول زیر هر یک از این محورها به همراه مثالی، آورده شدهاند.
| محور تقارن | شکل نمونه | طرح نمونه |
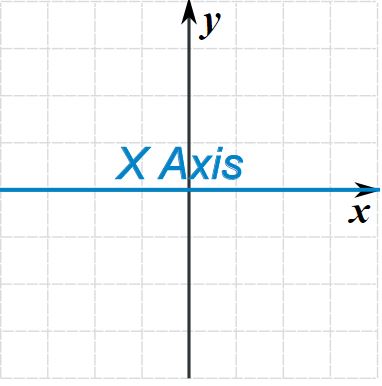 | 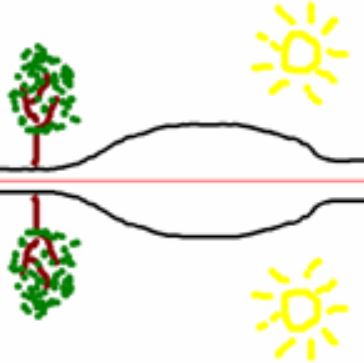 | 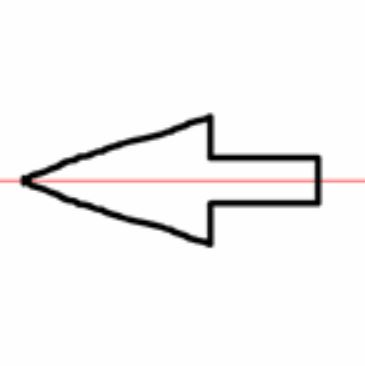 |
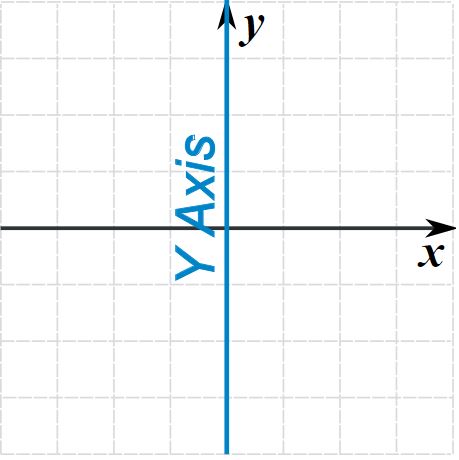 | 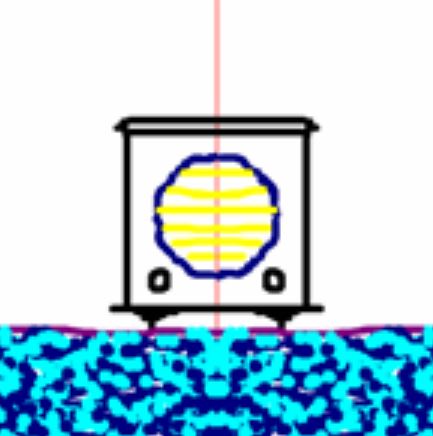 | 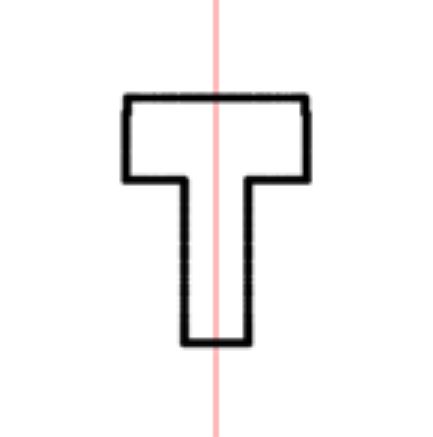 |
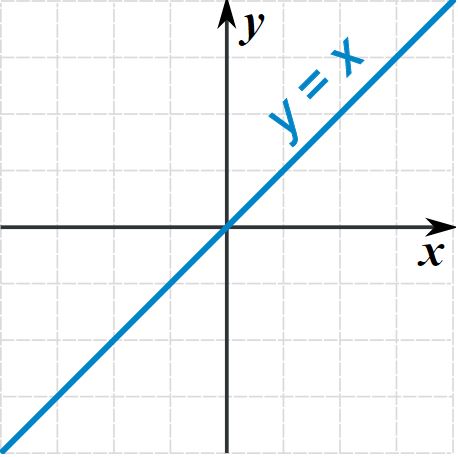 |  |  |
 |  |  |
آزمایش تا خوردگی
یک از راه های یافتن محور تقارن اشکال، تاکردن آن حول محوری دلخواه می باشد.
درصورتی که نیمه ی تاخورده شکل دقیقا بر نیمه دیگر آن منطبق شود (لبه ها کاملا برهم منطبق شوند)، بی شک خط تاخوردگی همان محور تقارن است.
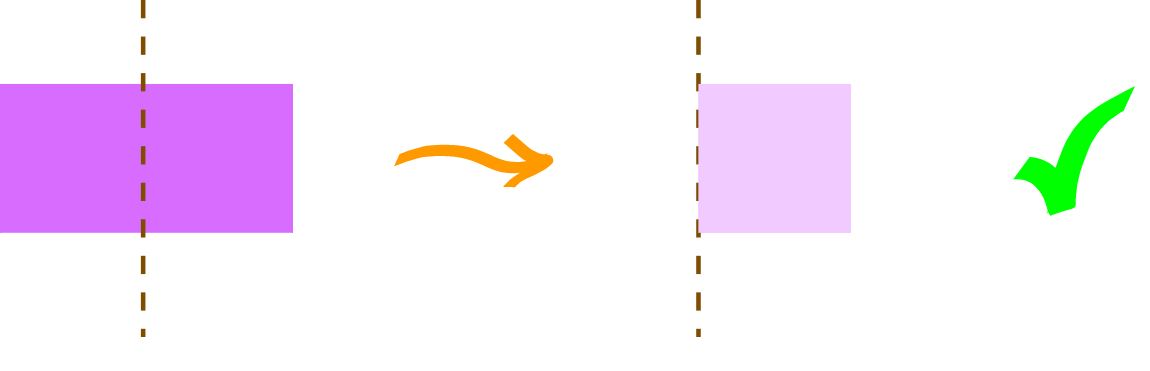
برای مثال اگر یک مستطیل را حول محور یکی از قطرهایش تا بزنید خواهید دید که دو نیمه برهم منطبق نخواهند شد.
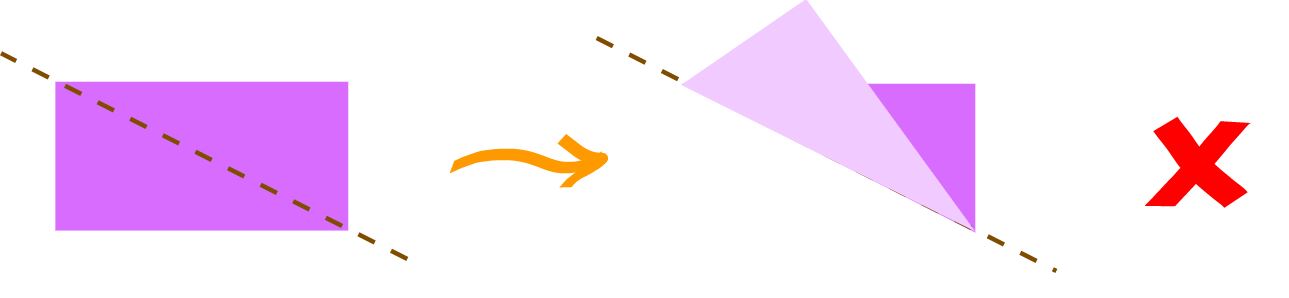
پس این خط، محور تقارن مستطیل نمیباشد. اما اگر همان مستطیل را به صورت زیر تا بزنید خواهید دید که دو نیمه کاملا همدیگر را میپوشانند و لبه ها بر هم منطبق میشوند.
چگونه میتوان انعکاس اشکال را حول محوری دلخواه ترسیم کرد؟
این کار به سادگی و به صورت گام به گام قابل انجام است. بایستی برای هر یک از اضلاع هندسهتان، مراحل زیر را طی کنید.
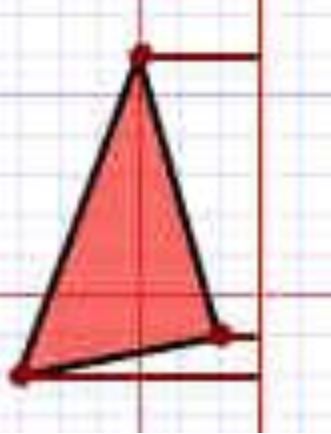
- فاصله عمودی میان رئوس هندسه و محور مرکزی را اندازه بگیرید.
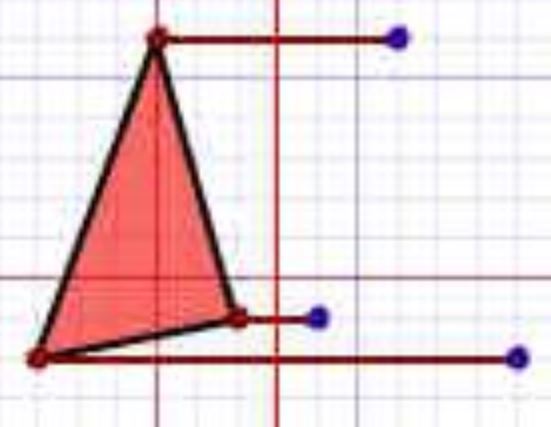
- نقطهای را به میزان فاصله اندازه گیری شده، در طرف دیگر محور ایجاد کنید.
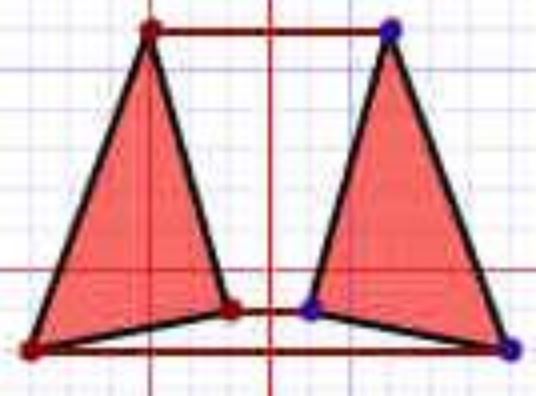
- در نهایت نقاط ایجاد شده را به یکدیگر متصل کنید.
انعکاس حول محور X
بدین منظور تنها بایستی مقادیر محور عمودی را در یک منفی ضرب کنید.
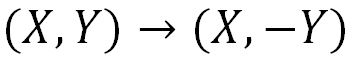
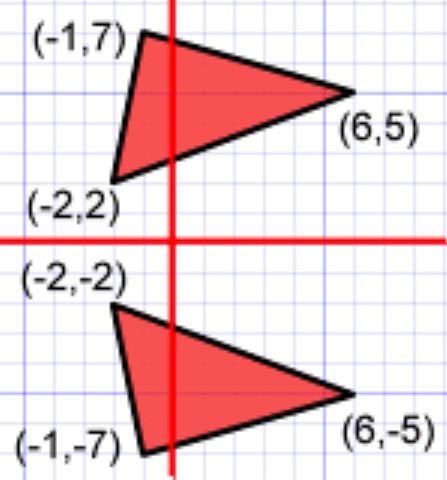
انعکاس حول محورY
بدین منظور تنها بایستی مقادیر محور افقی را در یک منفی ضرب کنید.
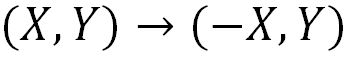
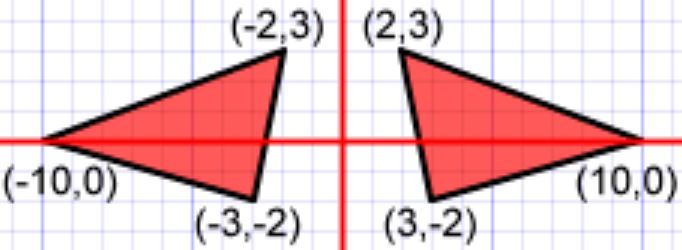
محور تقارن در مثلث
یک مثلث می تواند 1 تا 3 محور تقارن داشته باشد. همچنین نوعی از این شکل هندسی نیز وجود دارد که محور تقارنی ندارد.
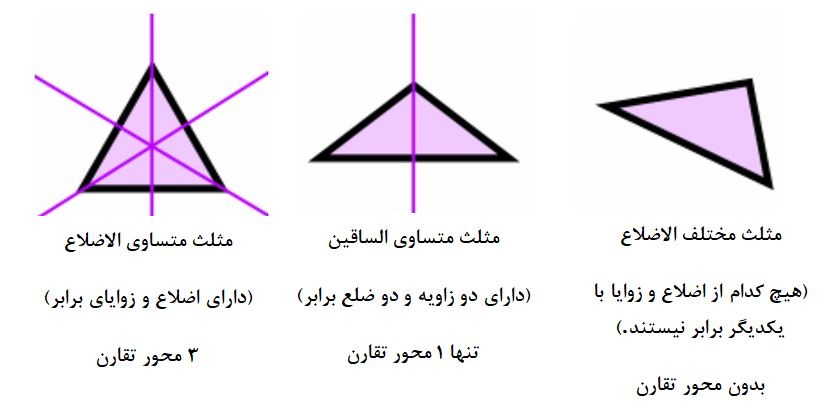
محور تقارن در چهارضلعی
چهارضلعیها نیز با توجه به موقعیت اضلاع و اندازه زوایا و اضلاع، می توانند 1، 2 یا 4 محورهای تقارن داشته باشند. همچنین حالتی نیز وجود دارد که چهارضلعی میتواند محور تقارنی نداشته باشد.
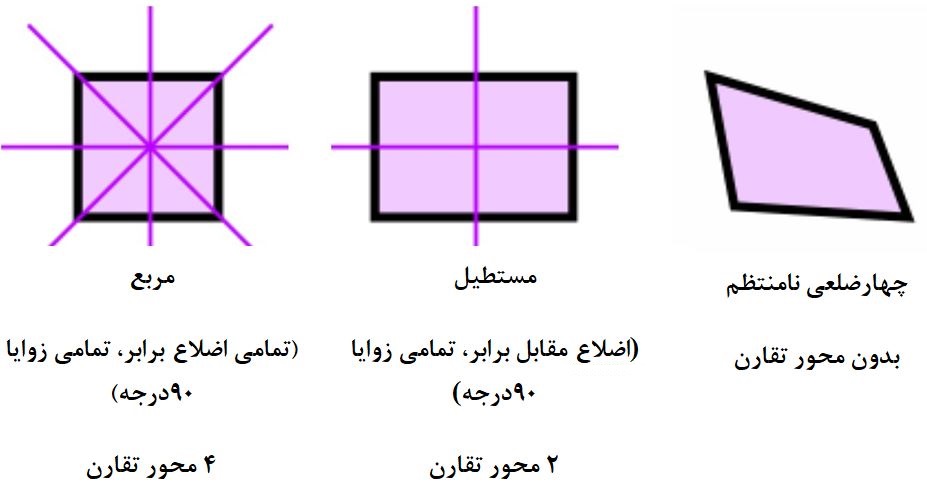
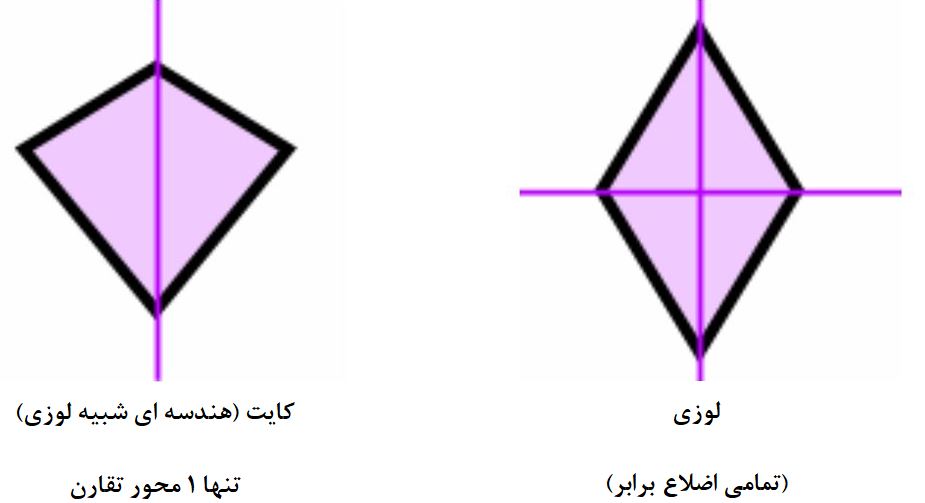
برای مطالعه بیشتر در زمینه چهارضلعیها به مطلب «چهار ضلعی ها — به زبان ساده» مراجعه کنید.
محور تقارن در چندضلعی منتظم
در اشکال چندضلعی منتظم، تمامی اضلاع و زوایا با هم برابرند.
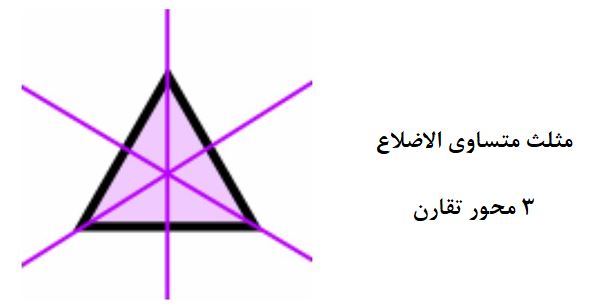
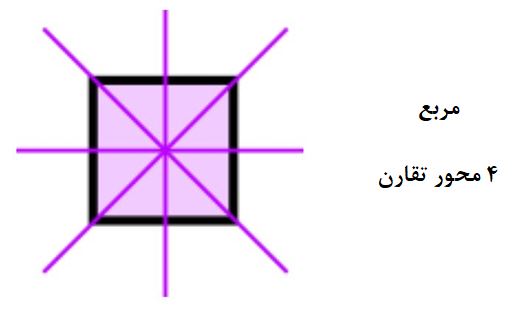
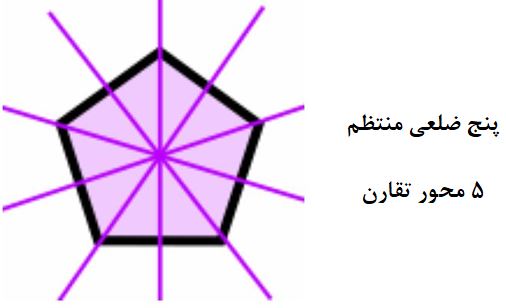
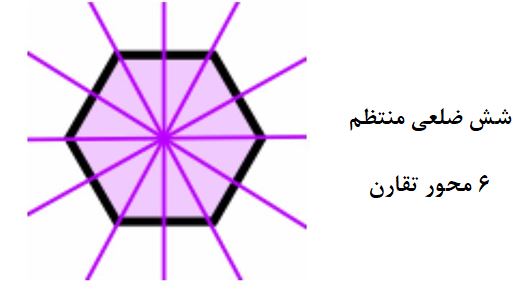
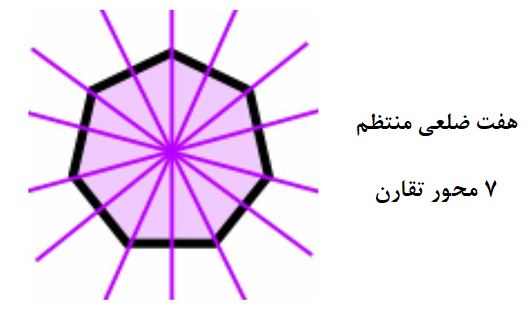
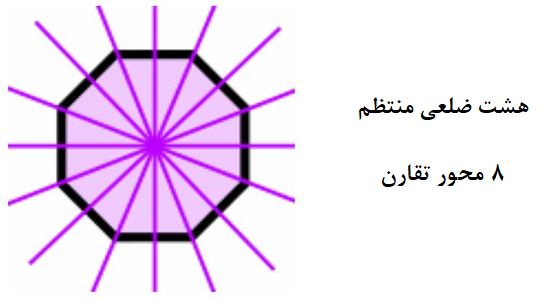
لازم به ذکر است که همین الگو ادامه پیدا میکند:
- یک چندضلعی منتظم با 9 ضلع، دارای 9 محور تقارن می باشد.
- یک چندضلعی منتظم با 10 ضلع، دارای 10 محور تقارن می باشد.
- ...
- و همینطور یک چندضلعی منتظم با n ضلع، دارای n محور تقارن می باشد.
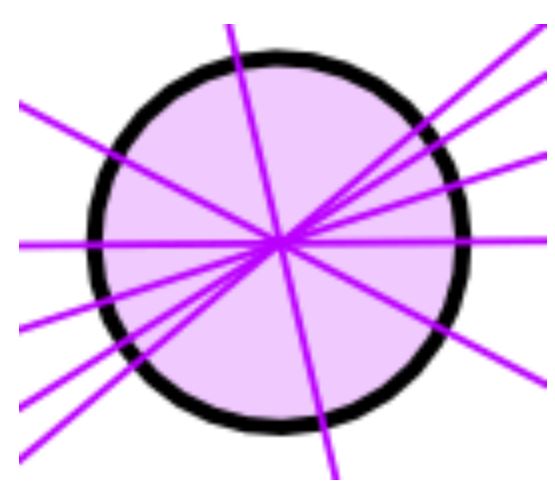
محور تقارن در دایره
در دایره هر خطی با هر زاویهای، در صورتی که از مرکز دایره عبور کند، یک محور تقارن خواهد بود. بنابراین یک دایره، بینهایت محور تقارن دارد.
اگر تمایل به مطالعه بیشتر در این موضوع داشته باشید، شاید آموزش های زیر نیز برای شما مفید باشند:
**











