پیش بینی قیمت سهام با مدل‌های ARIMA در پایتون و R — راهنمای کاربردی

«میانگین متحرک خودهمبسته یکپارچه» (Autoregressive Integrated Moving Average | ARIMA) ابزاری مهم در تحلیل «سری‌های زمانی» (Time Series) به منظور پیش‌بینی قیمت‌های آینده یک متغیر بر اساس مقدار کنونی آن به شمار می‌آید. در این مطلب، مجموعه داده قیمت سهام «جانسون و جانسون» (Johnson & Johnson | JNJ) از سال ۲۰۰۶ الی ۲۰۱۶ و مدل ARIMA برای انجام پیش‌بینی قیمت در سری‌های زمانی استفاده شده است.

میانگین متحرک خودهمبسته

هدف ARIMA شناسایی ماهیت روابط بین باقیمانده‌ها است که مدلی با درجه خاصی از قدرت پیش‌بینی را فراهم می‌کند. در اولین نمونه، به منظور انجام تحلیل سری‌های زمانی، باید مجموعه داده را با عبارت لگاریتمی تعریف کرد. اگر داده‌ها صرفا به صورت قیمت بیان شده‌اند، این کار برای ترکیب مداوم «بازگشت‌ها» (returns) در طول زمان منجر به نتایج گمراه کننده‌ای می‌شود.

فیلم آموزش پیش بینی قیمت سهام در بورس با شبکه عصبی عمیق LSTM در متلب در فرادرس

کلیک کنید

یک مدل ARIMA دارای مختصات‌های (p, d, q) است که هر یک در ادامه تشریح شده‌اند:

• P نشانگر تعداد عبارات خودهمبسته است. به عبارت دیگر، تعداد مشاهدات از مقادیر زمان گذشته است که برای پیش‌بینی مقادیر آینده مورد استفاده قرار می‌گیرند. برای مثال، اگر مقدار p برابر با ۲ باشد، این یعنی دو مشاهده زمانی قبلی در این سری برای پیش‌بینی «گرایش‌های آینده» مورد استفاده قرار می‌گیرند.
• d نشانگر تفاضل‌های (differences) مورد نیاز برای «ماناسازی» (Stationary) سری‌های زمانی است. (به عبارت دیگر، یک سری زمانی با میانگین ثابت، واریانس و خودهبستگی.) برای مثال، اگر d = 1 باشد، بدین معنا است که اولین تفاضل سری‌های زمانی برای تبدیل آن به سری مانا باید محاسبه شود.
• q نشانگر «میانگین متحرک» (moving average) خطای پیش‌بینی قبلی در مدل یا «مقادیر عقب مانده» (lagged values) از عبارت خطا است. به عنوان مثال، اگر q دارای مقدار ۱ باشد، بدان معنا است که ۱ مقدار عقب‌مانده از عبارت خطا در مدل وجود دارد.

پیاده‌سازی ARIMA با کتابخانه پایتون statsmodels

در اینجا، چگونگی پیاده‌سازی یک مدل ARIMA در پایتون با استفاده از کتابخانه‌های Pandas و statsmodels آموزش داده شده است.

فیلم آموزش تحلیل و پیش بینی سری های زمانی در فرادرس

کلیک کنید

۱. بارگذاری کتابخانه‌ها

ابتدا، کتابخانه‌های لازم بارگذاری می‌شوند. مهم‌ترین کتابخانه برای این مثال statsmodels است زیرا از آن برای محاسبه آمارهای ACF و PACF و همچنین فرموله کردن مدل ARIMA استفاده می‌شود.

1import pandas
2import matplotlib.mlab as mlab
3import matplotlib.pyplot as plt
4import numpy as np
5import math
6from statsmodels.tsa.stattools import acf, pacf
7import statsmodels.tsa.stattools as ts
8from statsmodels.tsa.arima_model import ARIMA

2. ایمپورت کردن فایل CSV و تعریف متغیر «price» با استفاده از Pandas

1variables = pandas.read_csv('jnj.csv')
2price = variables['price']

3. نمودارهای شاخص خودهمبستگی جزئی و شاخص خودهمبستگی

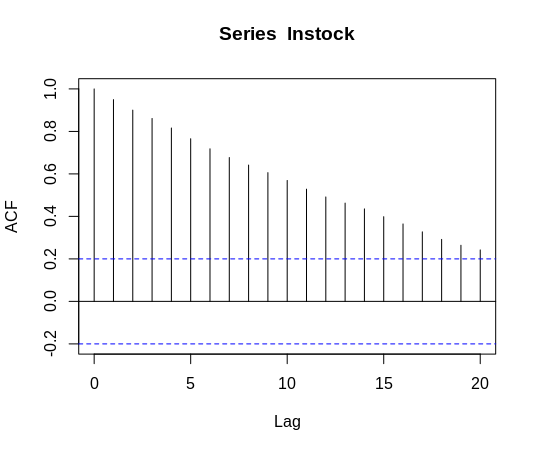
از تفسیر نمودارهای «شاخص خودهمبستگی جزئی» (Partial Autocorrelation | PACF) و «شاخص خودهمبستگی» (Autocorrelation | ACF) برای تعیین اینکه داده‌ها پس از تفاضل‌گیری مانا هستند یا خیر، استفاده می‌شود. تابع شاخص خودهمبستگی و خودهمبستگی برای «درجات مختلف» (Varying Degrees)، ضریب همبستگی را میان سری‌ها و تاخیر متغیرها در طول زمان اندازه‌گیری می‌کنند.

فیلم آموزش تجزیه و تحلیل و آماده سازی داده ها با پایتون Python در فرادرس

کلیک کنید

یک فرآیند هنگامی خودهمبسته است که سری زمانی یک الگوی خاص را دنبال کند که در آن مقدار کنونی به نوعی به مقدار (مقادیر) پیشین وابسته باشد. برای مثال، اگر بتوان از تحلیل رگرسیون برای تمایز مقدار کنونی یک متغیر از مقدار پیشین آن استفاده کرد، به آن فرایند (AR(1 گفته می‌شود.

1Xt = ß0 + ß1X(t-1) + et

این در حالی است که، نمونه‌هایی وجود دارد که در آن‌ها مقدار کنونی یک متغیر از دو یا سه مقدار قبلی که یک فرایند (AR(2 یا (AR(3 را به ترتیب ترکیب می‌کند قابل تشخیص است.

1Xt = ß0 + ß1X(t-1) + ß2X(t-2) + et
2Xt = ß0 + ß1X(t-1) + ß2X(t-2) + ß3X(t-3) + et

در ادامه، چگونگی تولید نمودارهای acf و pacf نشان داده شده است.

1lnprice=np.log(price)
2lnprice
3plt.plot(lnprice)
4plt.show()
5acf_1 =  acf(lnprice)[1:20]
6plt.plot(acf_1)
7plt.show()
8test_df = pandas.DataFrame([acf_1]).T
9test_df.columns = ['Pandas Autocorrelation']
10test_df.index += 1
11test_df.plot(kind='bar')
12pacf_1 =  pacf(lnprice)[1:20]
13plt.plot(pacf_1)
14plt.show()
15test_df = pandas.DataFrame([pacf_1]).T
16test_df.columns = ['Pandas Partial Autocorrelation']
17test_df.index += 1
18test_df.plot(kind='bar')
19result = ts.adfuller(lnprice, 1)
20result

می‌توان مشاهده کرد که statsmodels نمودارهای خودهمبستگی و خودهمبستگی جزئی را تولید می‌کند.

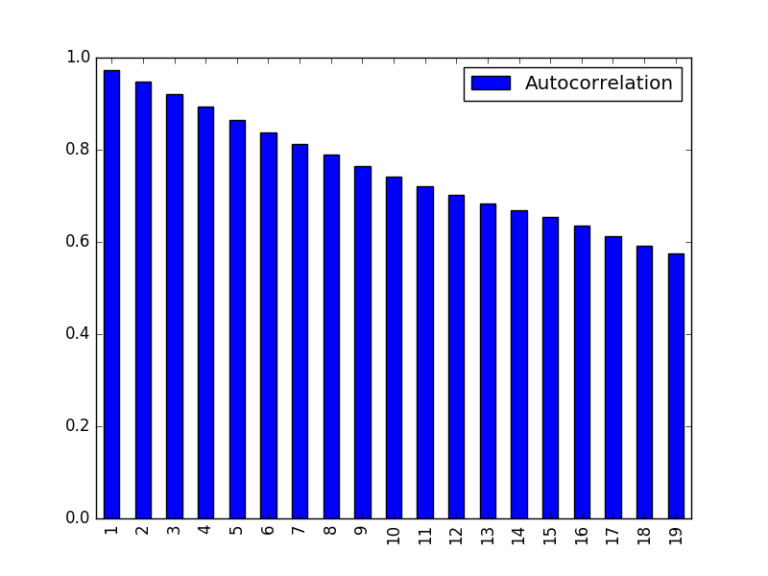
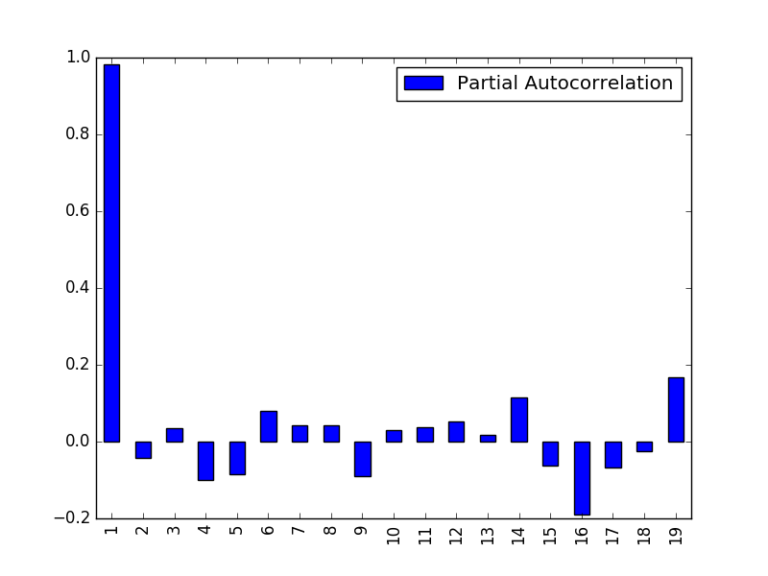
علاوه بر آن، این تصدیق وجود دارد که داده‌ها یک فرایند مانای (AR(1 را دنبال می‌کنند (یکی با میانگین، واریانس و شاخص خودهمبستگی ثابت) و می‌توان مشاهده کرد که نمودار قیمت اکنون یک فرآیند مانا را نشان می‌دهد.

1lnprice_diff=lnprice-lnprice.shift()
2diff=lnprice_diff.dropna()
3acf_1_diff =  acf(diff)[1:20]
4test_df = pandas.DataFrame([acf_1_diff]).T
5test_df.columns = ['First Difference Autocorrelation']
6test_df.index += 1
7test_df.plot(kind='bar')
8pacf_1_diff =  pacf(diff)[1:20]
9plt.plot(pacf_1_diff)
10plt.show()

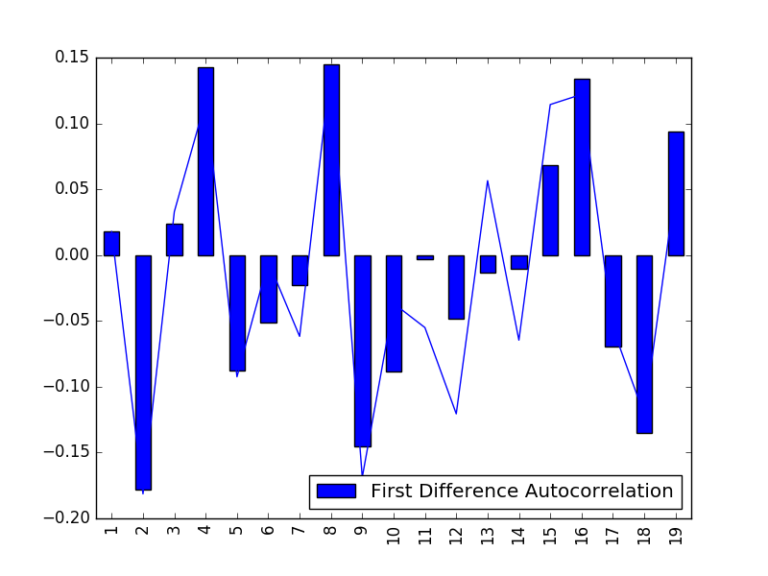
۴. تولید مدل ARIMA

1price_matrix=lnprice.as_matrix()
2model = ARIMA(price_matrix, order=(0,1,0))
3model_fit = model.fit(disp=0)
4print(model_fit.summary())

با استفاده از پیکربندی (۰ و ۱ و ۰)، مدل ARIMA تولید می‌شود.

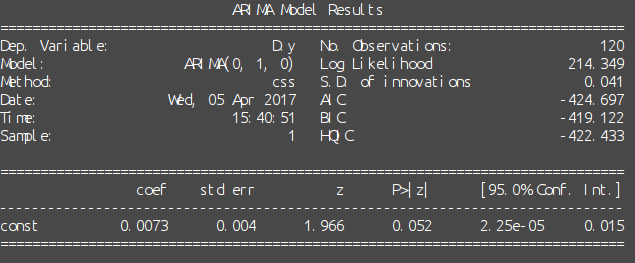
چنانکه پیش‌تر بیان شد، داده‌ها در قالب لگاریتمی هستند. به دلیل آنکه در این مثال کار تحلیل قیمت سهام انجام می‌شود، این قالب برای محاسبه بازده مرکب الزامی است. اگرچه، هنگامی که پیش‌بینی‌ها به دست آمد (برای هفت دوره در این مثال)، می‌توان پیش‌بینی قیمت واقعی را با تبدیل شکل لگاریتمی به نمایی به دست آورد.

1predictions=model_fit.predict(122, 127, typ='levels')
2predictions
3predictionsadjusted=np.exp(predictions)
4predictionsadjusted

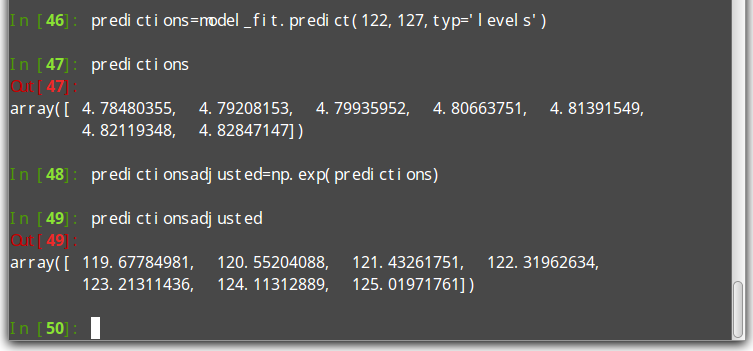
در این نمونه، پیش‌بینی مقادیر آینده انجام شده است، ودر ادامه backtest در R با جداسازی داده‌ها به داده‌های آموزش و آزمون انجام می‌شود. این کار برای تعیین اینکه پیش‌بینی‌های مدل چقدر صحیح هستند با مقایسه خروجی مدل (ساخته شده از داده‌های آموزش) به داده‌های تست انجام می‌شود.

ARIMA با R

اکنون، بررسی می‌شود که این مدل چگونه با استفاده از R پیاده‌سازی می‌شود. برای این مدل، ٪۸۰ از داده‌ها (۹۶ مشاهده اول) به عنوان مجموعه داده آموزش مورد استفاده قرار می‌گیرند تا مدل ساخته شود، در حالیکه داده‌های باقیمانده به عنوان داده‌های تست مورد استفاده قرار می‌گیرند تا صحت مدل اندازه‌گیری شود.

فیلم آموزش تحلیل و پیش بینی سری های زمانی در فرادرس

کلیک کنید

۵. تولید نمودارهای ACF و PACF

دوباره، نمودارهای ACF و PACF ترسیم می‌شوند.

1acf(lnstock, lag.max=20)
2pacf(lnstock, lag.max=20)

۶. تست Dickey–Fuller

به منظور استفاده از مدل ARIMA، اکنون تست رسمی‌تری برای تعیین اینکه آیا سری زمانی مانا است یا خیر مورد استفاده قرار می‌گیرد. به عبارت دیگر، آیا یک میانگین، واریانس و خودهمبستگی ثابت در سراسر مجموعه داده سری‌های زمانی وجود دارد. برای این منظور، از تست Dickey-Fuller استفاده می‌شود. در ٪۵ از سطح اهمیت داریم:

H0: سری‌های غیر مانا

HA: سری‌های مانا

1data:  lnstock
2Dickey-Fuller = -2.0974, Lag order = 4, p-value = 0.888
3alternative hypothesis: stationary

با مقدار P-Value برابر با ۰.۸۸۸ نمی‌توان «فرض صفر» (null hypothesis) از غیرمانایی را در سری رد کرد. اگرچه، هنگامی که داده‌ها «تفاضل‌گیری اول» (first-differenced) شدند، می‌توان مشاهده کرد که p-value  زیر 0.05 است و بنابراین می‌توان فرضیه صفر از غیر مانایی را رد کرد.

1data:  difflnstock
2Dickey-Fuller = -5.0751, Lag order = 4, p-value = 0.01
3alternative hypothesis: stationary

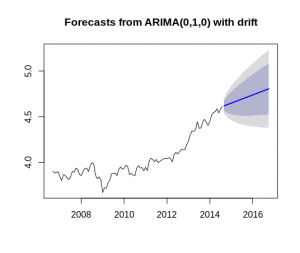
علاوه بر آن، تابع auto.arima در R برای هر دو مدل یک «گام تصادفی با انحراف» (random walk with drift) باز می‌گرداند، یعنی،  (ARIMA(0, 1, 0. بر این مبنا، می‌توان انتخاب کرد که یک مدل (ARIMA (0, 1, 0 برای هر دو سهام تعیین شود.

7. خروجی ARIMA

برای تولید یک نمودار ARIMA و خروجی با اجازه دادن به خود R برای تعیین پارامترهای مناسب با استفاده از ARIMA، می‌توان از تابع auto.arima به صورت زیر پس از تعریف سری زمانی استفاده کرد.

1pricearima <- ts(lnstock, start = c(2006,09), frequency = 12)
2fitlnstock<-auto.arima(pricearima)
3
4Series: pricearima 
5ARIMA(0,1,0) with drift         
6
7Coefficients:
8       drift
9      0.0075
10s.e.  0.0044
11
12sigma^2 estimated as 0.00182:  log likelihood=165.38
13AIC=-326.76   AICc=-326.63   BIC=-321.65

می‌توان مشاهده کرد که ARIMA در نهایت یک گام تصادفی با انحراف را برای سهام تشخیص می‌دهد؛ بدین معنا که حرکت قیمت سهام تصادفی است، اما یک الگوی هدفمند را در خلال زمان دنبال می‌کند. حرکت دارایی‌های مالی متعدد تصادفی به دست آمده است، که معمولا یک گام تصادفی با انحراف را دنبال می‌کند، بدین معنا که الگوهای هدفمند در کوتاه مدت نقش آفرین هستند و از این مورد می‌توان بهره‌برداری کرد.

توجه به این نکته لازم است که در یک شرایط ایده‌آل، ARIMAX به کار گرفته می‌شود که یک مدل ARIMA را با در نظر گرفتن «متغیرهای تصادفی» «explanatory variables» پیش‌بینی می‌کند. اگرچه، در شرایطی که هدف پیش‌بینی یک سری زمانی صرفا بر پایه مقادیر پیشین باشد، ARIMA مدل استانداردی برای انجام آن محسوب می‌شود. همچنین می‌توان، توان ln را در پیش‌بینی به منظور به دست آوردن قیمت واقعی محاسبه کرد.

1#Forecasted Values From ARIMA
2forecastedvalues_ln=forecast(fitlnstock,h=26)
3forecastedvalues_ln
4plot(forecastedvalues_ln)

1forecastedvaluesextracted=as.numeric(forecastedvalues_ln$mean)
2finalforecastvalues=exp(forecastedvaluesextracted)
3finalforecastvalues

طرح‌ریزی ۲۶ دوره، پیش‌بینی زیر را در عبارت exp به دست می‌دهد:

1> finalforecastvalues

[1] 101.4698 102.2290 102.9938 103.7644 104.5408 105.3230 106.1110 106.9049 107.7048 108.5106 109.3225 110.1404 110.9645 111.7947 112.6312 113.4739 114.3229 115.1782 116.0400 116.9082 117.7829 118.6641 119.5520 120.4465 121.3476 122.2556

۸. اعتبارسنجی Training-Test

1> df<-data.frame(price[96:121],finalforecastvalues)
2> col_headings<-c("Actual Price","Forecasted Price")
3> names(df)<-col_headings
4> attach(df)
5> percentage_error=((df$`Actual Price`-df$`Forecasted Price`)/(df$`Actual Price`))
6> percentage_error

 [1] -0.0074819537 -0.0038130090 -0.0004170119 -0.0433719063 -0.0976804738 -0.0728155807 -0.1013633836 -0.1252634992
[9] -0.1149107514 -0.1541401644 -0.1308660880 -0.2056309085 -0.2228489342 -0.1383453174 -0.1361083651 -0.1281169831
[17] -0.1178398054 -0.1099174498 -0.0873208758 -0.0575334338 -0.0521664682 0.0152039673 0.0389721026 -0.0092715631
[25] -0.0272381466 -0.0290005779

1> mean(percentage_error)

[1] -0.08151102

با توجه به خروجی‌های بالا، می‌توان مشاهده کرد که به طور میانگین ٪۰.۸ انحراف بین قیمت کنونی و قیمت پیش‌بینی شده توسط ARIMA وجود دارد.

۹. تست Ljung-Box

در حالیکه می‌توان از این مدل برای پیش‌بینی مقادیر آینده برای قیمت استفاده کرد، یک تست مهم که برای ارزیابی یافته‌های مدل ARIMA مورد استفاده قرار می‌گیرد Ljung-Box است.

فیلم آموزش تحلیل و پیش بینی سری های زمانی در فرادرس

کلیک کنید

اساسا، این تست برای تعیین اینکه باقی‌مانده سری زمانی یک الگوی تصادفی را دنبال می‌کند یا یک درجه خاصی از غیر تصادفی بودن دارد مورد استفاده قرار می‌گیرد.

• H0: باقیمانده دارای یک الگوی تصادفی است.
• HA: باقیمانده از یک الگوی تصادفی پیروی نمی‌کند.

شایان توجه است که این روش برای تعیین تعداد مشخصی از تاخیرها برای Ljung-Box می‌تواند کاملا دلخواه باشد. از این رو، در اینجا تست Ljung-Box با تاخیرهای ۵، ۱۰ و ۱۵ اجرا می‌شود. برای اجرای این تست در R، از توابع زیر استفاده می‌شود.

1> Box.test(fitlnstock$resid, lag=5, type="Ljung-Box")
2
3Box-Ljung test
4
5data:  fitlnstock$resid
6X-squared = 9.2542, df = 5, p-value = 0.09934
7
8> Box.test(fitlnstock$resid, lag=10, type="Ljung-Box")
9
10Box-Ljung test
11
12data:  fitlnstock$resid
13X-squared = 12.979, df = 10, p-value = 0.2249
14
15> Box.test(fitlnstock$resid, lag=15, type="Ljung-Box")
16
17Box-Ljung test
18
19data:  fitlnstock$resid
20X-squared = 15.395, df = 15, p-value = 0.4234

از خروجی بالا می‌توان مشاهده کرد که مقدار ناچیزی p-value در همه تاخیرها وجود دارد. این یعنی درجه بالایی از تصادفی بودن در باقی‌مانده‌ها وجود دارد (سازگار با مدل گام تصادفی با انحراف) و بنابراین مدل فاقد خودهمبستگی است.

اگر نوشته بالا برای شما مفید بوده، آموزش‌های زیر نیز به شما پیشنهاد می‌شود:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش‌های یادگیری ماشین و بازشناسی الگو
• مجموعه آموزش‌های شبکه‌های عصبی مصنوعی
• مجموعه آموزش‌های هوش محاسباتی
• مجموعه آموزش‌های برنامه نویسی پایتون (Python)
• آموزش برنامه‌نویسی R و نرم‌افزار R Studio
• مجموعه آموزش‌های برنامه نویسی متلب (MATLAB)

^^