آنالیز واریانس (ANOVA) یک و دو طرفه در R – راهنمای کاربردی
یکی از کاربردیترین روشهای آماری در تجزیه و تحلیل دادهها، تکنیک «تحلیل واریانس» یا «آنالیز واریانس» (Analysis of Variance) است که بطور خلاصه آنوا (ANOVA) نامیده میشود. در این روش، واریانس کل دادهها براساس یک یا چند متغیر عامل (Factor Variable) به دو یا چند بخش تفکیک شده است. براساس آزمونهای مربوط به واریانس میتوان همگون یا ناهمگون بودن گروهها را آزمود.
از تکنیک آنالیز واریانس یا تحلیل واریانس، در رگرسیون، آزمون میانگین و حتی خوشهبندی استفاده میشود. در این نوشتار به بررسی تحلیل واریانس یک و دو طرفه پرداخته و با استفاده از مثالها و کدهای R شیوه به کارگیری این تکنیک را فرا میگیریم.
برای آگاهی بیشتر از موضوعات و اصطلاحات به کار رفته در این متن، پیشنهاد میشود که مطلب تحلیل واریانس (Anova) — مفاهیم و کاربردها را مطالعه کنید. همچنین خواندن نوشتار آزمون فرض میانگین جامعه در آمار — به زبان ساده نیز خالی از لطف نیست.
آنالیز واریانس
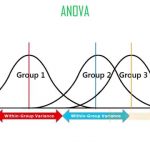
برای انجام آزمون مقایسه میانگین بین دو یا چند جامعه آماری مستقل، میتوان از روش «آنالیز واریانس» (ANOVA) استفاده کرد. آزمون ANOVA براساس «منبع تغییرات» (Source of Variation) و تجزیه آن بین و درون دستهها یا گروهها عمل میکند.
شکل اولیه آزمون ANOVA، به بررسی برابری میانگین بین دو یا چند جامعه مستقل میپردازد. اگر تغییرات «در بین گروهها» (Between Group) نسبت به تغییرات «درون گروهها» (Within Group) زیاد نباشد، میتوان به یکسان بودن میانگین گروهها رای داد.
به این ترتیب مشخص میشود که تحلیل یا آنالیز واریانس، یک نسخه توسعه یافته برای آزمون میانگین T test در زمانی است که تعداد جامعه یا گروهها بیش از ۲ باشند. مشخص است که در اینجا متغیری که گروهها را مشخص میکند یک متغیر عامل یا فاکتور است.
با توجه به وجود یک یا دو متغیر عامل در تحلیل واریانس، آن را یک طرفه (One-way ANOVA) یا دو طرفه (Two-way ANOVA) مینامند.
آنالیز واریانس یک طرفه (One-way ANOVA)
در بسیاری از تحلیلهای آماری، نیاز است که میانگین بین چندین گروه مقایسه و آزمون شود. با انجام آنالیز واریانس مشخص میشود که آیا گروهها در حقیقت از یک جامعه هستند یا هر گروه به یک جامعه آماری متفاوت تعلق دارد. این آزمون، به مانند دیگر آزمونهای آماری، براساس شواهد و نمونه سعی در رد فرض صفر دارد. در صورتی که فرض صفر رد نشود، خواهیم گفت که نمونه شاهدی بر رد فرض صفر ندارد. در آزمون آنالیز واریانس فرضیههای آزمون به صورت زیر نوشته میشوند.
در اینجا k تعداد گروهها است. همچنین نشان میدهد که حداقل یکی از تساویهای مربوط به فرض برقرار نیست.
نکته: تفاوت عمده بین آزمون ANOVA و T test زمانی است که بیشتر از دو گروه برای مقایسه وجود داشته باشد. در حالتی که دو گروه برای آزمون میانگین معرفی شود، هر دو آزمون T test و ANOVA نتایج یکسانی خواهند داشت.
برای مثال فرض کنید در بخش فروش یک شرکت، قرار است کارایی و توانایی فروش سه گروه A, B, C از فروشندهها بررسی شود. فرض کنید گروه A فروشندههای با تجربه، گروه B فروشندههای تازه کار و گروه C نیز فروشندگان اینترنتی هستند. به این ترتیب میخواهیم بسنجیم آیا میانگین فروش این سه گروه یکسان است یا با یکدیگر از لحاظ آماری تفاوت دارند.
به این ترتیب باید دو متغیر را برای هر فروشنده اندازهگیری کنیم.
- گروه فروشنده: متغیر فاکتور یا عامل با مقدارهای A, B, C
- میزان فروش: متغیر کمی که کارایی را نشان میدهد. از این متغیر برای محاسبه میانگین فروش برای هر گروه استفاده میکنیم.
فرضیههای این آزمون به صورت زیر نوشته میشود:
میانگین هر سه گروه یکسان است
حداقل میانگین یکی از گروهها با دو گروه دیگر متفاوت است
مشخص است که فرض نشان میدهد که براساس نمونه، دلیل کافی برای نابرابری میانگین گروهها وجود ندارد و در مقابل فرض بیان میکند که دلیل کافی برای برابری بین میانگین گروهها وجود ندارد.
آنالیز واریانس، شرایط و نحوه عملکرد
هنگام اجرای آزمون آنالیز واریانس (ANOVA) باید از وجود شرایط اجرای آن که در ادامه دیده میشود، اطمینان داشته باشیم.
- نمونههای حاصل از هر گروه یا جامعه، تصادفی و از توزیع نرمال باشند.
- واریانسهای گروهها برابر ولی نامشخص هستند.
- گروهها از یکدیگر مستقل هستند.
مانند هر آزمون دیگر، آنالیز واریانس نیز احتیاج به یک آماره آزمون دارد. آماره آزمون برای ANOVA دارای توزیع F است. این آماره نسبت تغییرات «بین گروهها» (Between Groups) به «درون گروهی» (Within Groups) را اندازهگیری میکند.
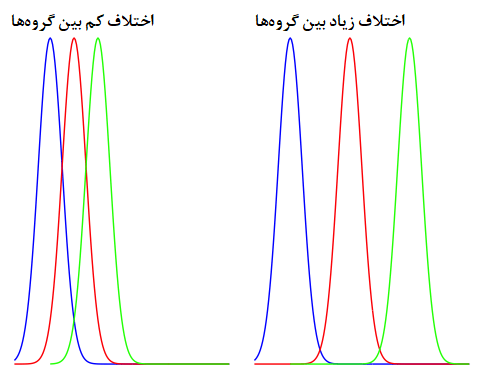
تغییرات بین گروهها (Between Groups)، بیانگر اختلافات بین گروهها است. تصویر زیر برای درک بهتر این مفهوم مناسب است. همانطور که دیده میشود، در نمودارهای سمت چپ، بین میانگین گروهها اختلاف زیادی وجود ندارد. در حالیکه در سمت راست، میانگین گروهها دارای اختلاف محسوسی است.
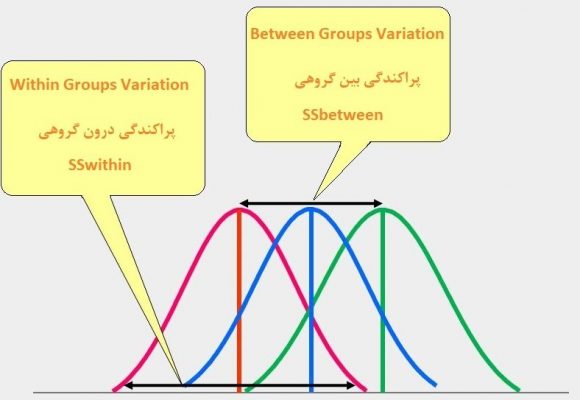
از طرف دیگر تغییرات درون گروهی (Within Groups) تحت تاثیر پراکندگی اعضای هر گروه قرار دارد. در حقیقت مجموع مربعات اختلاف دادههای هر گروه نسبت به میانگین آن گروه مقدار محاسبه شده و حاصل برای همه گروهها با یکدیگر جمع میشود. در تصویر زیر این مفهوم مشخص شده و پراکندگی درون گروهی و بین گروهی بطور کامل نشان داده شده است.
مقدار F براساس این دو خصوصیات محاسبه میشود. اگر میانگین پراکندگی بین گروهی را با و میانگین پراکندگی درون گروهی را با نشان دهیم، مقدار آماره F را به صورت زیر محاسبه میکنیم.
بزرگ بودن مقدار F نشانهای برای رد فرض صفر است، زیرا مشخص است که صورت بزرگتر از مخرج است. در نتیجه گروهها دارای پراکندگی بین گروهی بیشتری نسبت به پراکندگی درون گروهها هستند. به این ترتیب متوجه میشویم که جوامعی که این گروهها را تشکیل میدهند، یکسان نیستند. از آنجایی که توزیع نرمال و واریانس نیز ثابت در نظر گرفته شده است، تنها عاملی که باعث تفاوت بین جامعهها است، میانگین است. پس فرض صفر که برابری میانگین گروهها را نشان میهد، رد خواهد شد.
همچنین کوچک بودن مقدار F بیانگر معنا دار نبودن اختلاف بین میانگین گروهها است. در نتیجه به نظر میرسد که همه گروهها از یک جامعه آماری هستند، پس میانگینشان با هم برابر است.
برای آشنایی با نحوه اجرای تحلیل یا آنالیز واریانس در زبان برنامهنویسی R از یک مثال کمک میگیریم. فرض کنید با یک مجموعه داده با ۴۸ سطر و ۳ ستون (متغیر) مواجه هستیم که مربوط به زمان اثر سم به یک نوع خوک (Guinea) با توجه به نوع سم (Poison) و نحوه درمان خوکها (Treat)، است.
کدهایی که در ادامه دیده میشود به منظور فراخوانی این اطلاعات از اینترنت و آماده سازی آنها برای تحلیل واریانس نوشته شده است.
نکته: برای اجرای این کد باید به اینترنت متصل باشید. مشخص است که کتابخانه dplyr نیز فراخوانی شده است. بنابراین باید این کتابخانه را روی R نصب کرده باشید.
همانطور که مشخص است در سه گام این اطلاعات ثبت شدهاند. در گام اول این اطلاعات با قالب csv از سایت گیتهاب (raw.githubusercontent.com)، فراخوانی شده و در چارچوب داده df ثبت شدهاند. سپس متغیر X که شامل شماره ردیف مشاهدات است از df حذف شده است. در گام سوم نیز متغیر poison به عنوان متغیر عامل تغییر یافته. در انتها نیز مجموعه داده df با استفاده از دستور glimpse به صورت یک لیست افقی ظاهر میشود.
مشخصات مربوط به ۴۸ «مشاهده» (Observation) و سه «متغیر» (Variables) در لیست دیده میشود. مشخص است که متغیر time طول عمر ۴۸ خوک Guinea پس از تزیق سم است. نوع سم نیز به صورت یک متغیر عامل یا فاکتور با سه سطح با مقدارهای ۱ تا ۳ در متغیر دوم مشخص شده است. همچنین نوع درمان Treat نیز به عنوان متغیر سوم با سطوح A, B, C, D دیده میشود.
هدف از این بررسی، آزمون با فرضهای زیر است:
تفاوت معنیداری بین میانگین طول عمر خوکها براساس نوع سم وجود ندارد
حداقل یکی از سمها باعث کوتاهتر شدن میانگین طول عمر خوکها میشود
به بیان دیگر میخواهیم بدانیم که آیا نوع سم در کاهش طول عمر خوکها موثر است یا خیر. برای انجام این کار مراحل زیر را طی میکنیم.
- گام اول- تعیین متغیر فاکتور (که در اینجا متغیر سم و نوع درمان هستند)
- گام دوم- محاسبه شاخصهای مهم آماری برای طول عمر
- رسم نمودار جعبهای به منظور مقایسه شاخصها و توزیع طول عمر براساس نوع سم (مقایسه سه گروه مختلف)
- انجام تحلیل یا آنالیز واریانس
- انجام آزمون مقایسهای دو تایی TukeyHSD
آنالیز واریانس و گامهای اجرای آن
در ادامه به انجام هر یک از این گامها میپردازیم و نتایج را تفسیر و بررسی میکنیم.
گام اول
هر چند در مرحله اولیه، متغیر نوع سم را به متغیر فاکتور تبدیل کردیم ولی بهتر است بطور کلی قبل از اجرای تحلیل واریانس، مشخصات متغیر فاکتور را تشخیص و در صورت نیاز اصلاح کنیم. دستور levels سطوح مختلف متغیر عامل را نشان میدهد.
به این ترتیب خروجی به صورت زیر است. مشخص است که هر دو متغیر به عنوان متغیر فاکتور یا عامل در نظر گرفته شدهاند. سطوح هر یک از متغیرهای عامل نیز دیده میشود. متغیر «سم» (poison) دارای سه سطح با مقدارهای از ۱ تا ۳ و متغیر «درمان» (treat) دارای چهار سطح با مقدارهای متنی از A تا D است.
گام دوم
برای محاسبه میانگین و انحراف استاندارد از کد زیر کمک بگیرید. توابع group_by و summarise از کتابخانه dplyr فراخوانی شدهاند.
با اجرای این دستورات میانگین و انحراف استاندارد طول عمر براساس سه گروهی که نوع سم را مشخص میکنند، محاسبه شده و در خروجی ظاهر خواهد شد. به نظر میرسد که واریانس یا انحراف استاندارد sd_time در بین دو گروه اول و دوم تقریبا یکسان ولی در گروه سوم با بقیه متفاوت است.
گام سوم
رسم یک نمودار جعبهای (Boxplot) در درک توزیع و مقایسه توزیع سه جامعه، کمک فراوانی میکند. برای رسم این نمودار از تابع ggplot استفاده شده است. کد زیر به این منظور تهیه شده است.
نکته: اگر کتابخانه ggplot2 بر روی R نصب نشده باشد، رسم نمودار امکانپذیر نیست. بنابراین بهتر است قبلا این کتابخانه را با دستور نصب کرده باشید.
در نمودار نیز وجود اختلاف در واریانس گروه سوم با دو گروه دیگر به خوبی نشان داده شده است. ولی از آنجایی که در مثال، مناقشه نیست از این مشکل میگذریم و فرض میکنیم که واریانس در بین سه گروه برابر است.
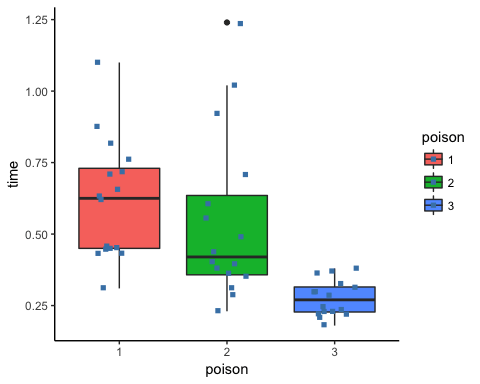
گام چهارم
برای اجرای آزمون آنالیز واریانس یک طرفه یا One-way ANOVA باید از تابع aov به شکل زیر استفاده کنید. چند پارامتر مهم در این تابع در جدول زیر معرفی شدهاند.
| پارامتر | عملکرد |
| formula | نحوه ارتباط بین متغیر عامل و متغیر پاسخ براساس اسامی موجود در مجموعه داده |
| data | مجموعه داده به کار گرفته شده |
منظور از متغیر پاسخ، متغیر کمی است که باید میانگینش بین گروهها مقایسه و آزمون شود. برای مشخص کردن رابطه در پارامتر formula باید از علامت ~ بین متغیر عامل و متغیر پاسخ کمک بگیرید. همچنین برای تعیین نحوه ارتباط بین متغیرهای عامل و متغیر پاسخ از علامت + برای نشان دادن رابطه اثرات اصلی متغیرها و از علامت * برای نشان دادن اثرات اصلی و متقابل متغیرهای عامل روی متغیر پاسخ استفاده کنید. با توجه به اینکه در این مثال فقط از یک متغیر عامل استفاده خواهیم کرد، شکل و قالب برای نمایش رابطه بین متغیر عامل و پاسخ به صورت زیر خواهد بود.
بنابراین دستور مناسب برای اجرای آنالیز واریانس برای مثال به صورت زیر نوشته خواهد شد. همچنین خروجی در متغیر anova_one_way ذخیره و نتیجه حاصل از آنالیز واریانس با دستور summary ظاهر میشود.
با اجرای آخرین دستور، جدول آنالیز واریانس ظاهر میشود. مقدار پراکندگی و میانگین پراکندگی درون و بین گروهی در ستون Mean Sq و همینطور مقدار F و همچنین مقدار که همان مقدار احتمال (p-value) است، نیز در ستونهای آخر دیده میشوند.
براساس مقدار احتمال که با علامت *** مشخص شده، معلوم میشود که فرض صفر یعنی برابر بودن میانگین در سه گروه در سطح آزمون کمتر از 0.05 نیز رد میشود. بنابراین نوع سم در طول عمر خوکها تاثیرگذار است. به این ترتیب متوجه خواهیم شد که حداقل یکی از سمها باعث کاهش طول عمر خوکها شده است. ولی سوالی که اینجا مطرح میشود آن است که کدام سم باعث ایجاد این اختلاف شده؟ آیا میانگین طول عمر با نوع سم اول کاهش یافته یا با نوع سم دوم؟ یا هر یک از سمها میانگین طول عمر مخصوص به خود را دارند.
مقایسههای دو تایی
همانطور که در خروجی دستور aov دیده شد، تحلیل واریانس، مشخص نمیکند که کدام یک از گروهها باعث ایجاد اختلاف هستند. بنابراین برای تشخیص مبنای تفاوت دست به مقایسههای دو تایی میزنیم.
در اینجا از روش توکی استفاده میکنیم که در R با تابع TukeyHSD امکان پذیر است. پارامترهای این دستور به صورت زیر است.
| پارامتر | عملکرد |
| x | خروجی حاصل از یک مدل (معمولا نتیجه حاصل از aov) |
| which | یک بردار متنی شامل عاملهایی که باید در فاصلههای اطمینان برایشان محاسبه شود. |
| ordered | مقدار منطقی به منظور مرتب سازی میانگینها و مقایسه گروهها با گروهی که کمترین میانگین را دارد. |
| conf.level | سطح اطمینان به منظور تشکیل فاصله اطمینان برای تفاضل میانگین مقایسههای دو تایی |
به این ترتیب کافی است که به عنوان پارامتر در این تابع، از خروجی aov استفاده کنید. مقدار پیشفرض برای conf.level نیز ۹۵٪ است. بنابراین فاصلههای اطمینان ۹۵٪ برای تفاضل میانگین مقایسههای دوتایی خواهیم داشت.
خروجی به صورت زیر خواهد بود.
مقایسههای دوتایی در ستون اول این خروجی مشخص شده است. براساس ستون آخر که مقدار احتمال (p-value) را برای آزمون اختلاف میانگین دو گروه نشان میدهد، متوجه میشویم که اختلاف بین دو گروه ۱ و ۳ و همچنین ۲ و ۳ معنیدار است زیرا مقدار احتمال برایشان کمتر از 0.05 است. ولی در مقایسه گروه ۲ و ۱ مشخص می شود که این دو دارای اختلاف معنیداری نیستند.
این موضوع را در نمودار جعبهای نیز به وضوح میتوان دید. در نمودار جعبهای میزان همپوشانی بین دو گروه ۱ و ۲ بسیار زیاد است ولی بین گروههای ۱ و ۳ و همینطور ۲ و ۳ همپوشانی در جعبهها وجود ندارد.
همینطور اگر کرانهای فاصله اطمینان یعنی lwr و upr شامل صفر باشند، یعنی اولی منفی و دومی مثبت باشد، میانگین دو گروه یکسان در نظر گرفته میشود. در غیراینصورت فاصله اطمینان نشانگر وجود اختلاف بین میانگین دو گروه است.

آنالیز واریانس دو طرفه (Two-way ANOVA)
در تحلیل واریانس دو طرفه، یک متغیر عامل دیگر نیز به مدل اضافه میشود. به این ترتیب در این مدل تاثیر دو متغیر عامل بر روی متغیر پاسخ را طبق فرمول زیر معرفی میکنیم.
در اینجا متغیر پاسخ و متغیرهای عامل هستند. البته در این حالت اثرات متقابل هر دو متغیر عامل بر روی متغیر پاسخ نادیده گرفته شده است.
فرضیات مربوط به آزمون آنالیز واریانس دو طرفه با اثرات اصلی به صورت زیر نوشته میشود.
نماد نشانگر میانگین مقدار طول عمر براساس گروههایی است که متغیر عامل اول (نوع سم) ایجاد میکند. به این ترتیب نماد نیز بیانگر میانگین طول عمر گروههایی است که براساس متغیر عامل دوم (نوع درمان) ایجاد شدهاند.
در صورتی که احتیاج دارید اثرات متقابل را نیز مشخص کنید، فرمول را به صورت زیر بنویسید.
بطوری که متغیر کمی یا پاسخ و متغیرهای طبقهای یا فاکتور هستند. اگر مدل همراه با اثرات متقابل باشد، فرضیات مربوط به آزمون آنالیز واریانس دو طرفه به صورت زیر نوشته میشود.
مشخص است که k تعداد سطوح متغیر عامل اول و l تعداد سطوح متغیر عامل دوم است. در نتیجه فرضیه همزمان باید مورد بررسی قرار گیرند.
در ادامه مثال قبلی، فرض کنید که متغیر دوم (نوع درمان treat) را هم اضافه کردهایم. یعنی میخواهیم تحت نوع سم و شیوه درمان، میانگین طول عمر خوکها را بدون در نظر گرفتن اثر همزمان نوع سم و شیوه درمان، مقایسه کنیم. کد زیر به این منظور نوشته شده است.
به این ترتیب خروجی به صورت زیر خواهد بود. مشخص است که نوع سم (سه نوع سم) و همچنین شیوه درمان با (چهار شیوه درمان) در میانگین طول عمر خوکها موثر هستند.
مقدار احتمال (p-value) یا همان نشان میدهد که هر دو عامل (نوع سم و نوع درمان) بر روی میانگین طول عمر تاثیر گذار هستند. همانطور که دیده میشود، مقدار مجموع مربعات (Sim Sq) و میانگین مربعات (Mean Sq) برای متغیر سم (poison) در حالت آنالیز واریانس یک و دو طرفه برابر است ولی از آنجایی که محاسبه مقدار F برای هر یک از حالتها متفاوت است، مقدار F و همچنین در حالت یک طرفه با دو طرفه فرق خواهد داشت. اگر لازم باشد که اثرات متقابل این دو عامل نیز لحاظ شود از کد دستوری زیر استفاده میکنیم.
به این ترتیب اثرات همزمان هر دو عامل نیز بررسی میشود. خروجی به صورت زیر است.
همانطور که دیده میشود، هر دو متغیر به طور مستقل بر روی متغیر پاسخ تاثیر گذارند ولی اثر همزمان و متقابل متغیرهای عامل، بر روی متغیر پاسخ وجود ندارد، زیرا مقدار احتمال یا بزرگتر از 0.1 است.
نکته: اثرات متقابل شامل اثرات اصلی متغیرهای عامل نیز هست. بنابراین اگر فرمول مربوط به مدل را به صورت زیر نیز بنویسید، نتیجه با بالا یکسان خواهد بود.
خلاصه
به منظور جمعبندی نحوه اجرای تحلیل یا آنالیز واریانس یک و دو طرفه و شیوه پارامتر دهی تابع aov در R، جدول زیر را تهیه کردهایم.
| آزمون | کد | فرض مقابل | شرح آزمون |
| آنالیز واریانس یک طرفه | aov(y~x,data=df) | حداقل میانگین یکی از گروهها با بقیه متفاوت است. | مقایسه میانگین دو یا چند گروه مستقل با توزیع نرمال و واریانس برابر |
| مقایسههای دوتایی | TukeyHSD(aov summary) | اختلاف میانگین دو گروه مخالف صفر است. | پس آزمون آنالیز واریانس. سطح خطای مقایسههای همزان دوتایی در سطح کنترل شده. |
| آنالیز واریانس دو طرفه | حداقل میانگین یکی از عوامل با بقیه متفاوت است. | آنالیز واریانس دو طرفه یا اثرات اصلی و متقابل متغیرهای عامل |
اگر این مطلب برای شما مفید بوده است و علاقهمند به یادگیری بیشتر در این زمینه هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- مجموعه آموزشهای نرمافزارهای آماری
- آموزش آمار و احتمال مهندسی
- آموزش برنامهنویسی R و نرمافزار R Studio
- آموزش تکمیلی برنامهنویسی R و نرمافزار RStudio
- آموزش آزمون های فرض مربوط به میانگین جامعه نرمال در SPSS
- آزمون تی (T Test) در R — راهنمای کاربردی
^^













سلام. بسیار روان و ساده و قابل درک توضیح داده اید.
تشکر فراوان
سلام وقت شما بخیر، میخواستم بپرسم برای آنالیز آزمایشات فاکتریل در قالب طرح کاملا تصادفی که سه فاکتور داره چطوری باید با آنوا کار کرد؟
نحوه وارد کردن داده ها مثل sas هست یا متفاوته؟
agar interaction significat bashe chi?
azoome taghibi chi hast?
سلام ممنونم از مطلب شما
ولی اینجا یک نکته برایم مبهم است .
اگر پرسشنامه ای داشته باشیم که مجموع 8 سوال در باره اعتبار سنجی الگو باشد وبین 30 نفر توزیع کنیم .آیا روش واریانس آنوا مناسب است ؟ در این پرسشنامه کدام گروه و کدام متغیر هستند ؟ ممنون از پاسخگویی شما
سلام
دو گروه که یک محصول تولید می کنند یکی میانگین نزدیک تر به میانگین بهینه دارد و یکی انحراف معیار کمتری دارد چگونه می توان گفت عملکرد کدام گروه بهتر است؟
سلام واریانس یک مشاهده برابراست با….
1صفر
2یک
3مبهم
4بستگی به تعریف واریانس داره
میشه لطفا جواب بدین
سپاس از شما استاد گرامی برای این مطالب دقیق و توضیحات شفاف شما.
با سلام و احترام
سپاس بابت مطلب آموزشی مفیدتون
یه سوال
در کد اول علامت %>% چه کاری انجام میده
من تو R انجام دادم خطا میگیرد
بسیار ممنونم از پاسخ شما
من dplyr را نصب کردم. ولی نمی دونم مثلا در کنار و انتهای کد df <- read.csv(PATH)
%<% چه کاری را انجام میدهد.
بازم سپاسگزارم از پاسخگویی شما.
سلام و درود بر شما مخاطب گرامی،
نصب بسته های مربوطه برای اجرای دستورات نرمافزار R لازم است. برای استفاده از دستورات انباشه مثل %>% باید از کتابخانه با بسته dplyr را روی نرمافزار نصب و فرخوانی کرده باشید.
تندرست و پیروز باشید.
ممنون بابت این آموزش
امکان داره که این قسمت رو بیشتر توضیح بدید؟
“همانطور که دیده میشود، هر دو متغیر به طور مستقل بر روی متغیر پاسخ تاثیر گذارند ولی اثر همزمان و متقابل متغیرهای عامل، بر روی متغیر پاسخ وجود ندارد”
این که دو متغییر به صورت مستقل اثر گذارند ولی همزمان اثر گذار نیستند به چه معنی هست؟
سلام و وقت بخیر به شما همراه مجله فرادرس؛
از این که مطلب «آنالیز واریانس (ANOVA) یک و دو طرفه درR — راهنمای کاربردی» نظرتان را جلب کرده است، خرسندیم.
توجه داشته باشید که هر یک از متغیرهای عامل ممکن است روی متغیر پاسخ اثر گذار باشند ولی حضور هر دو آنها به طور همزمان، تغییرات اضافی روی متغیر پاسخ نداشته باشد. برای مثال اگر فرض کنید با افزایش چربی خون فشار خون افراد افزایش مییابد. همچنین این اثر نیز با افزایش قند خون نیز رخ میدهد. ولی اگر هر دو عامل در یک بیمار حضور داشته باشد، اثر متقابلی بین آنها وجود ندارد. به این معنی فرض کنید که افزایش قند خون یک درجه و افزایش چربی خون به طور متوسط نیم درجه باعث افزایش فشار خون میشود. بنابراین کسی که هر دو مورد را داشته باشد، بطور متوسط ۱.۵ درجه افزایش در فشار خون خواهد داشت. ولی اگر اثر متقابل هر دو عامل وجود داشت، انتظار داشتیم که این فرد بیش از ۱.۵ درجه افزایش فشار خودن را تجربه کند.
از همراهی شما با مجله فرادرس بسیار سپاسگزاریم.
شاد و تندرست و پیروز باشید
بسیار عالی بود. تنها سایتی که به زبان فارسی کد نویسی در نرم افزار R را توضیح داد، سایت شما بود. متشکرم