تکانه زاویه‌ ای چیست؟ — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در بخش اول مبحث تکانه، در مورد اصول این مفهوم فیزیکی بحث کردیم. در این قسمت قصد داریم تا بخشی از این مفهوم تحت عنوان «تکانه زاویه ای» (Angular Momentum) را مورد تجزیه و تحلیل قرار دهیم.

تکانه زاویه ای یک ذره

ذره‌ای به جرم m، بردار مکانی r (نسبت به مبدا مختصات) و سرعت v را در نظر بگیرید. این ذره مطابق با شکل زیر حول مبدا، دوران می‌کند.

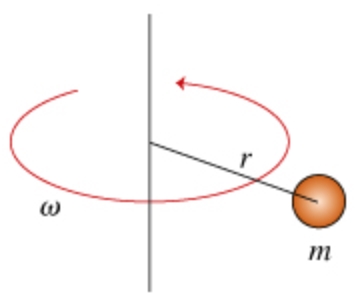
طبق مفاهیم بیان شده در بخش اول، ذره مفروض در هر لحظه دارای تکانه‌ای خطی برابر با p=mv است. از اصول بیان شده می‌دانیم که تغییرات تکانه نسبت به زمان برابر با نیروی وارد شده به ذره است. بنابراین می‌توان گفت:

$$f={dp \over dt}$$

فیلم آموزش فیزیک پایه 1 – جامع و کاربردی در فرادرس

کلیک کنید

f، برآیند نیروهایی است که به ذره، وارد می‌شوند. بنابراین این نیرو را می‌توان با استفاده از مشتق‌گیری زمانی تکانه ذره، محاسبه کرد. اما شاید توجه کرده باشید که بردار سرعت در این مسئله، با گذشت زمان، تغییر می‌کند. بنابراین به راستی چگونه بایستی از تکانه ذره‌ متحرک روی دایره، مشتق گرفت؟

بدین منظور، عددی تحت عنوان تکانه زاویه ای تعریف می‌شود که با حرف L نشان داده شده و برابر با مقدار زیر است.

L=r×p

همان‌طور که می‌بینید، این مقدار، برابر با ضرب خارجی دو بردار است؛ هم‌چنین از ریاضیات می‌دانیم که حاصل ضرب خارجی دو بردار، یک بردار است. بنابراین تکانه زاویه ای نیز مقداری برداری محسوب می‌شود که اندازه آن برابر با مقدار زیر است.

L= rpsin (θ)

در این رابطه θ، برابر با زاویه بین بردار r و سرعت ذره است. جهت بردار L، هم بر بردار سرعت و هم بر r عمود شده و با قانون دست راست می‌توان آن را تعیین کرد. مطابق با شکل زیر برای تعیین جهتِ بردارِ تکانه زاویه ای، انگشتان دست راست را در جهت بردار r گرفته و سپس آن‌ها در جهت دوران بچرخانید. حال انگشت شستتان، جهت بردار تکانه زاویه ای را نشان می‌دهد.

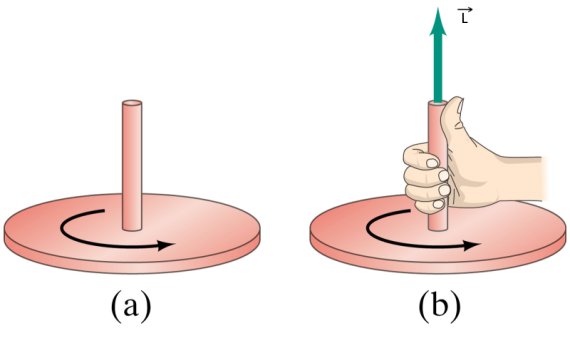
تغییرات تکانه زاویه ای نسبت به زمان

فرض کنید از رابطه مربوط به تکانه زاویه ای، مشتق گرفته می‌شود. در این حالت می‌توان گفت:

$$L=r×p \rightarrow {dL \over dt}=\dot r×p+r×\dot p$$

فیلم آموزش فیزیک 1 دانشگاهی با رویکرد حل مساله در فرادرس

کلیک کنید

توجه داشته باشید که مشتق‌گیری از ضرب خارجی، مشابه با حالت عادی است، با این تفاوت که در ضرب خارجی، ترتیب عبارات بایستی حفظ شوند. می‌دانیم که حاصل مشتق زمانی مکان، سرعت خواهد بود و مشتق زمانی تکانه، نیرو را به ما خواهد داد. با توجه به مفاهیم بیان شده می‌توان گفت:

$$\dot r=v={p \over m} \enspace \enspace (1)$$
$$\dot p = f \enspace \enspace (2)$$

$$(1) , (2) \rightarrow {dl \over dt}= {p×p \over m}+r×f$$

می‌دانیم که ضرب خارجی یک بردار در خودش صفر است؛ بنابراین عبارت اول در معادله بالا صفر خواهد بود. هم‌چنین از مکانیک می‌دانیم که حاصل‌ضرب خارجی بردار نیرو در مکان، برابر با گشتاور است. بنابراین تغییرات تکانه زاویه ای با زمان، به شکل زیر محاسبه می‌شوند.

r×f=τ

$${dl \over dt}=τ$$

برای جرم m که به فاصله r از مرکز، دوران می‌کند، مقدار تکانه زاویه ای برابر با مقدار زیر است.

l=mvr=mωr²

توجه داشته باشید که در این معادله، ω سرعت زاویه ای جرم مذکور است.

قانون پایستگی تکانه زاویه ای

بر خلاف تکانه خطی، تکانه زاویه ای هم به جرم دوران کننده و هم به نحوه توزیع آن اطرف جرم، وابسته است. در بخش لختی دورانی بیان کردیم که نحوه توزیع جرم، حول محور‌ها را با استفاده از خاصیتی تحت عنوان لختی دورانی بیان می‌کنیم. بنابراین تکانه زاویه ای به لختی دورانی وابسته است.

فیلم آموزش مکانیک تحلیلی 1 مرور و حل مثال در فرادرس

کلیک کنید

ذره‌ای را تصور کنید که حول محور ثابتی دوران می‌کند. طبعا ذره مفروض دارای تکانه زاویه ای است. قانون پایستگی تکانه زاویه ای بیان می‌کند که، در صورتی که گشتاوری به یک سیستم دورانی مفروض وارد نشود، تکانه زاویه ای آن تغییر نخواهد کرد. اگر لختی دورانی سیستمی را برابر با I و سرعت دورانی آن حول محور مشخصی را ω فرض کنیم، تکانه زاویه ای را می‌توان برابر با مقدار زیر محاسبه کرد.

L=Iω

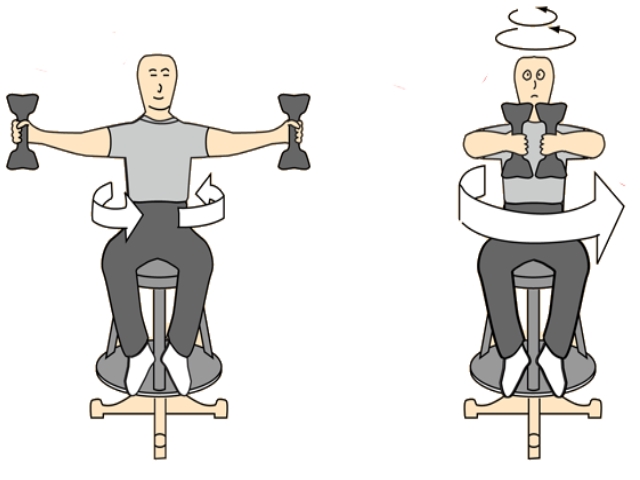
قانون پایستگی تکانه زاویه ای می‌گوید، در صورتی که گشتاوری به سیستم دورانی وارد نشود، تکانه زاویه ای آن ثابت می‌ماند. به عنوان مثال در ورزش اسکیت‌ سواری روی یخ، با جمع کردن دستان، I (لختی دورانی) بدن کم می‌شود. بنابراین برای ثابت ماندن L، سرعت زاویه ای (ω) بایستی افزایش یابد.

مثال ۱

برای نمونه مطابق با شکل زیر ورزشکاری را تصور کنید که روی یک صندلی با سرعت ۵۴۰ درجه در ثانیه به دور خود می‌چرخد. ناگهان این شخص دستان خود را به نحوی جمع می‌کند که لختی دورانی او $${2 \over 3}$$ برابر می‌شود. در این حالت سرعت زاویه ای این ورزشکار را بیابید؟

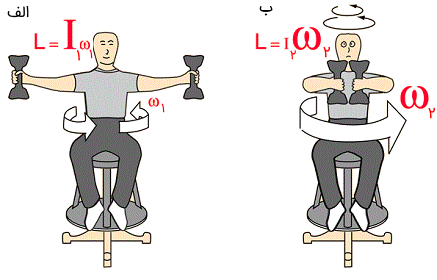
از آنجایی که تکانه زاویه ای در حالت دست باز و دست بسته، ثابت است، می‌توان گفت:

$$L=I_1ω_1=I_2ω_2$$

بنابراین سرعت زاویه ای در حالت دوم را می‌توان به‌شکل زیر محاسبه کرد.

$$L=I_1×540={2 \over 3}I_1ω_2 \rightarrow ω_2= {3 \over 2}×540=810 \enspace deg/s$$

در صورتی که به مباحث مرتبط در زمینه مهندسی مکانیک علاقه‌مند هستید، احتمالا می‌توانید از آموزش‌ها زیر استفاده کنید:

• لختی دورانی چیست -- به زبان ساده
• تکانه زاویه ای سیستم -- از صفر تا صد
• قوانین حرکت نیوتن - به زبان ساده
• تکانه چیست؟ -- به زبان ساده