محاسبه معیار ارزیابی AIC در R — به زبان ساده

در دیگر نوشتارهای فرادرس با عنوان معیار ارزیابی AIC در مدل‌های احتمالی --- از صفر تا صد مفهوم ارزیابی مدل و شیوه اندازه‌گیری آن توسط معیار AIC آشنا شدید. در این نوشتار ابتدا با مفهوم تابع درستنمایی بیشتر آشنا شده و سپس نحوه محاسبه معیار ارزیابی AIC در زبان برنامه‌نویسی محاسباتی R را مرور کرده و براساس این زبان و توابع کتابخانه‌ای R، به بررسی تابع درستنمایی و شیوه بدست آوردن AIC برای مقایسه مدل‌های تصادفی می‌پردازیم.

به این منظور بهتر است با بعضی از دستورات این زبان برای مدل‌سازی در نوشتارهای روش‌های رگرسیون در R — کاربرد در یادگیری ماشین (قسمت اول) و روش‌های رگرسیون در R — کاربرد در یادگیری ماشین (قسمت دوم) آشنا شوید. همچنین خواندن مطلب توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس که به معرفی چند توزیع احتمالی برای پدیده‌های تصادفی می‌پردازد، نیز خالی از لطف نیست.

محاسبه معیار ارزیابی AIC در R

یکی از شاخص‌های ارزیابی مدل‌های آماری «معیار ارزیابی آیکاکی» (Akaike Information Criterion - AIC) است که برحسب «تابع درستنمایی» (Likelihood Function) محاسبه می‌شود. با توجه به وابستگی AIC به تابع درستنمایی ابتدا به بررسی این تابع پرداخته و سعی می‌کنیم با مفهوم آن براساس محاسباتی که در R‌ انجام می‌دهیم، بیشتر آشنا شویم.

فیلم آموزش خوشه بندی K میانگین K-Means با اس پی اس اس SPSS در فرادرس

کلیک کنید

تابع درستنمایی (Likelihood Function)

فرض کنید بوسیله کد زیر، ۵۰ نمونه تصادفی از توزیع نرمال با میانگین $$\mu=a$$ و انحراف معیار $$\sigma=sdy$$ تولید شده است و برای نمایش فراوانی و توزیع داده‌ها نیز یک «هیستوگرام» (Histogram) ترسیم کرده‌ایم.

1set.seed(126)
2n <- 50 #sample size
3a <- 5
4sdy <- 3
5y <- rnorm(n, mean = a, sd = sdy)
6hist(y)

مشخص است که در این داده‌ها، مقدار میانگین جامعه آماری a<-۵ و انحراف معیار آن نیز sdy<-۳ در نظر گرفته شده است.

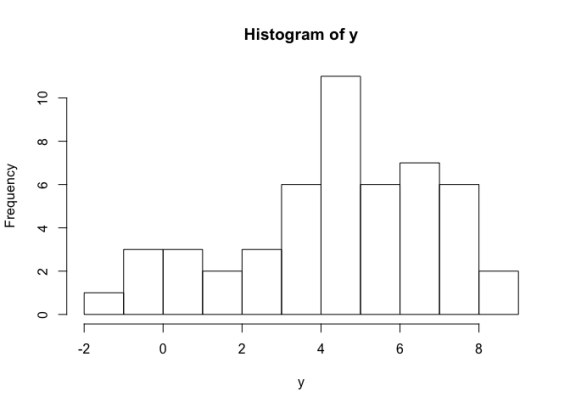
حال قرار است که بوسیله این نمونه تصادفی، پارامتر توزیع متغیر تصادفی $$Y$$ را مشخص کنیم. کدی که در ادامه مشاهده می‌کنید به منظور برآورد پارامترهای میانگین و واریانس براساس نمونه قبلی، برای یک جامعه آماری با توزیع نرمال نوشته شده است. همانطور که مشخص است پارامتر family برابر با مقدار gaussian در نظر گرفته شده تا بیانگر توزیع نرمال باشد.

1m1 <- glm(y ~ 1, family = "gaussian")
2sm1 <- summary(m1)
3print(sm1)

خروجی این کد به صورت زیر خواهد بود. مشخص است که برآورد پارامترهای میانگین در این خروجی $$intercept=4.3837$$ و واریانس $$Dispersion = 5.910122$$ است که در نتیجه جذر آن که انحراف معیار را نشان می‌دهد برابر با $$2.43$$ خواهد بود.

1Call:
2glm(formula = y ~ 1, family = "gaussian")
3
4Deviance Residuals: 
5    Min       1Q   Median       3Q      Max  
6-5.7557  -0.9795   0.2853   1.7288   3.9583  
7
8Coefficients:
9            Estimate Std. Error t value Pr(>|t|)    
10(Intercept)   4.3837     0.3438   12.75   <2e-16 ***
11---
12Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
13
14(Dispersion parameter for gaussian family taken to be 5.910122)
15
16    Null deviance: 289.6  on 49  degrees of freedom
17Residual deviance: 289.6  on 49  degrees of freedom
18AIC: 233.72
19
20Number of Fisher Scoring iterations: 2

همانطور که دیده می‌شود، مقدار AIC نیز که موضوع این مطلب است، در انتهای جدول، محاسبه و برابر با 233.72 نشان داده شده است.

نکته: برای استخراج برآورد پارامترهای توزیع آماری این مقدارها می‌توانید از دستورات زیر نیز کمک بگیرید.

1coef(m1)
2sm1$dispersion
3sqrt(sm1$dispersion)

باید توجه داشت که در اینجا داده‌ها از یک جامعه با میانگین ۵ و انحراف معیار ۳ تولید شده‌اند و برآوردها نیز بسیار به مقدارهای واقعی نزدیک هستند. در گام بعدی مقدار توزیع نرمال را در نقطه $$7$$ به کمک برآوردهای حاصل از مرحله قبل بدست می‌آوریم. همانطور که دیده می‌شود از دستور dnorm که برای محاسبه تابع چگالی توزیع نرمال در یک نقطه خاص استفاده می‌شود، کمک گرفته‌ایم.

1sdest <- sqrt(sm1$dispersion)
2dnorm(7, mean = coef(m1), sd = sdest)
3
4## [1] 0.09196167

این مقدار (0.09196167) همان مقدار تابع احتمال (Likelihood) برای مقدار $$7$$ برحسب میانگین و انحراف معیار برآورد شده است. به این ترتیب به نظر می‌رسد که محاسبه تابع درستنمایی براساس مشاهدات صورت گرفته و مقدار آن از نمونه‌ به نمونه‌ای دیگر متفاوت است. در کدی که در زیر مشاهده می‌کنید تابع درستنمایی برای مشاهدات مختلف ترسیم شده است. مشخص است که این نمودار اگر برحسب متغیر بودن مشاهدات تصور شود، همان تابع چگالی توزیع نرمال خواهد بود.

1plot(y, dnorm(y, mean = coef(m1), sd = sdest), ylab = "Likelihood")

محور افقی در این نمودار از مقدارهای مختلف $$y$$ (نمونه‌های تصادفی) تشکیل شده است. از طرفی محور عمودی نیز مقدار تابع چگالی احتمال را برای هر نقطه نمایش می‌دهد.

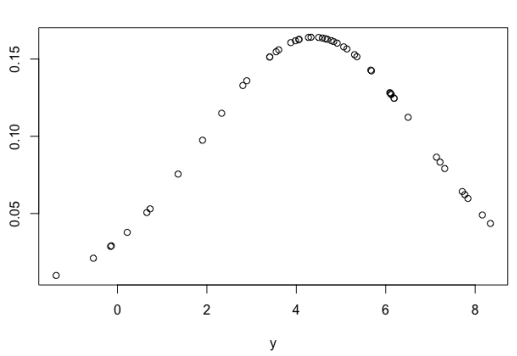
حال اگر بخواهیم برای چندین نمونه تصادفی، تابع احتمال توام را مشخص کنیم با فرض استقلال نمونه‌ها و متغیرهای تصادفی، حاصلضرب تابع احتمال برای متغیرهای تصادفی (نمونه‌های مختلف) می‌تواند بیانگر توزیع توام باشد. در این حالت با توجه به یکنوا بودن تابع لگاریتم می‌توانیم از لگاریتم حاصلضرب تابع توزیع توام استفاده کنیم تا نتیجه به جای حاصلضرب صورت حاصل جمع لگاریتم تابع احتمال هر یک از نمونه‌ها در آید. این کار را به کمک کد زیر انجام داده‌ایم.

1y_lik <- dnorm(y, mean = coef(m1), sd = sdest, log = TRUE)
2sum(y_lik)
3
4## [1] -114.8636

همانطور که دیده شد، ابتدا برای نمونه‌های تصادفی مختلف ($$y$$) تابع احتمال محاسبه شده سپس لگاریتم آن بدست آمده است. به این ترتیب برای انجام تحلیل روی تابع درستنمایی از لگاریتم تابع درستنمایی که به صورت مجموع لگاریتم توابع درستنمایی هر نمونه نوشته می‌شود، استفاده خواهیم کرد. مشخص است که مقدار تابع درستنمایی براساس نمونه تصادفی 50 تایی تولید شده، برابر با 114.8636- است.

نکته: از آنجایی که مقدارهای مربوط به تابع درستنمایی به مانند تابع چگالی محاسبه می‌شوند، معمولا در فاصله صفر تا یک قرار می‌گیرند در نتیجه لگاریتم آن‌ها منفی است. به همین دلیل در اغلب موارد مقدار لگاریتم تابع درستنمایی منفی است.

$$\large L(\theta_0)=\max L(\theta) \rightarrow  \ln (L(\theta_0))= \max \ln (L(\theta))$$

مقایسه فرضیه‌های مختلف به کمک تابع درستنمایی

فرض کنید قرار است اثر متغیرهای $$x۱$$ و $$x2$$ را روی $$y$$ مشخص کنیم. منظورمان از میزان اثر، قابلیت پیش‌بینی متغیر $$y$$ برحسب متغیرهای $$x1$$ و $$x2$$ است. قطعه کدی که در ادامه مشاهده می‌کنید به این منظور تهیه شده است.

فیلم آموزش خوشه بندی سلسله مراتبی در آر R در فرادرس

کلیک کنید

البته فرض بر این است که بین متغیر $$x1$$ و $$y$$ یک رابطه تقریبا خطی با معادله $$y=a+b*x1$$ و مقداری نوفه (Noise) برقرار است. تولید متغیر $$y$$‌ توسط دستور $$y <- a + b*x1 + rnorm(n, sd = sdy)$$ انجام شده است.

1a <- 5
2b <- 3
3n <- 100
4x1 <- rnorm(n)
5x2 <- rnorm(n)
6sdy <- 1
7y <- a + b*x1 + rnorm(n, sd = sdy)
8par(mfrow = c(1,2))
9plot(x1, y)
10plot(x2, y)

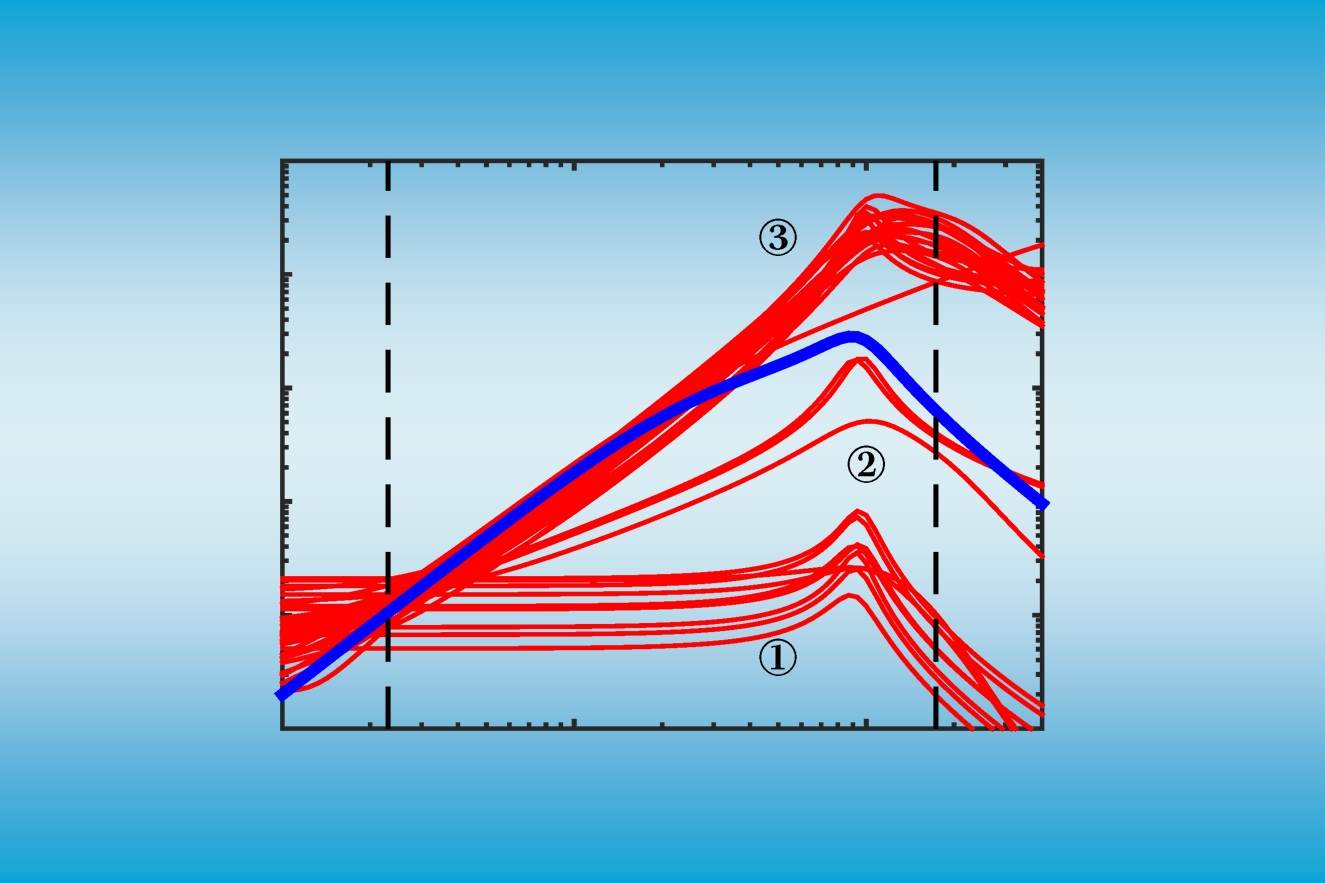
نتیجه اجرای این کد نمودارهایی است که در ادامه مشاهده می‌کنید. واضح است قدرت پیش‌بینی متغیر $$x1$$ برای $$y$$ بسیار بیشتر از قدرت پیش‌بینی متغیر $$x2$$ روی $$y$$‌ است.

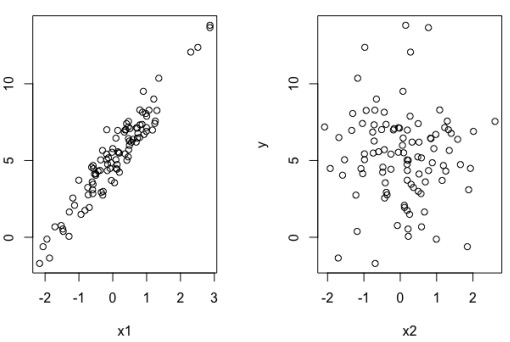
این امر را می‌خواهیم بوسیله مدل‌بندی و تابع glm در R‌ نیز نشان دهیم. به این منظور سه مدل را در نظر می‌گیریم. در مدل اول ($$m1$$) اثر متغیر $$x1$$ روی $$y$$ مشخص می‌شود. در مدل دوم ($$m2$$) تاثیر متغیر $$x2$$ بر $$y$$ اندازه‌ گرفته شده و در مدل سوم ($$m3$$) اثرات متغیرهای $$x1$$ و $$x2$$ بر متغیر وابسته $$y$$ مورد تحلیل قرار می‌گیرد. دستوراتی که در ادامه دیده می‌شوند، برای ایجاد این مدل‌ها در R نوشته شده‌اند.

1m1 <- glm(y ~ x1)
2m2 <- glm(y ~ x2)
3m3 <- glm(y ~ x1 + x2)

به این ترتیب به کمک دستورات زیر نمودار ارتباط و خط پیش‌بین برای دو مدل اول و دوم را ترسیم می‌کنیم.

1plot(x1, y)
2lines(x1, predict(m1))
3
4plot(x2, y)
5lines(x2, predict(m2))

مشخص است که به علت آنکه مدل سوم به صورت سه بعدی است، نمودار آن را رسم نکرده‌ایم.

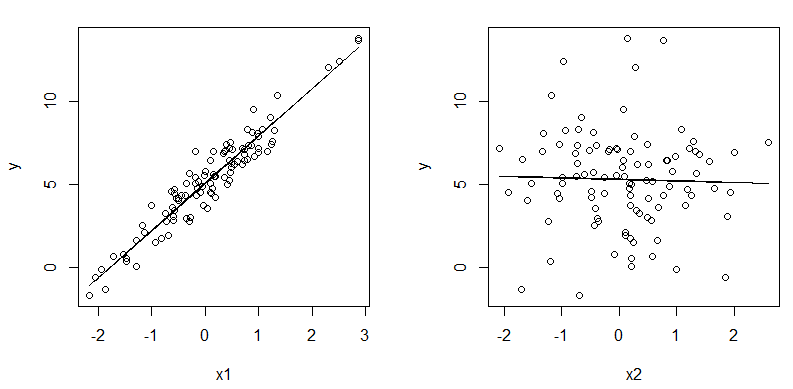
در ادامه، کدهایی را می‌بینید که برای نمایش پارامترهای مدل‌های ایجاد شده لازم است. همچنین در انتها نیز مقدار لگاریتم تابع درستنمایی توسط جمع (sum) برای هر مدل محاسبه شده است.

1sm1 <- summary(m1)
2sum(dnorm(y, mean = predict(m1), sd = sqrt(sm1$dispersion), log = TRUE))
3
4## [1] -125.6214
5
6sm2 <- summary(m2)
7sum(dnorm(y, mean = predict(m2), sd = sqrt(sm2$dispersion), log = TRUE))
8
9## [1] -247.8059
10
11sm3 <- summary(m3)
12sum(dnorm(y, mean = predict(m3), sd = sqrt(sm3$dispersion), log = TRUE))
13
14## [1] -125.4843

نکته: توجه کنید که پارامتر انتهایی تابع dnorm به صورت log=TRUE باعث می‌شود که لگاریتم تابع چگالی برای هر نمونه محاسبه شود. در نتیجه مجموع این مقدارها همان لگاریتم تابع درستنمایی (لگاریتم چگالی توام متغیرهای تصادفی) است.

همانطور که می‌بینید، مدلی که دارای بزرگترین مقدار تابع لگاریتم درستنمایی باشد، مناسب‌ترین مدل در بین این سه مدل خواهد بود. بنابراین مدل اول و سوم به نظر مناسب هستند و مدل دوم با مدل مناسب بسیار فاصله دارد. البته با توجه به اینکه میزان فاصله لگاریتم تابع درستنمایی برای مدل اول و سوم زیاد نیست و از طرفی مدل $$m1$$ دارای متغیرهای کمتر در نتیجه ساده‌تر است، استفاده از آن بر مدل $$m3$$‌ ترجیح دارد. به نظر می‌رسد که احتیاج به معیاری داریم که بتواند تعداد پارامترها را هم در محاسبات شرکت دهد و ما را به نتیجه دلخواه برساند. از آنجایی که در شیوه محاسبه AIC این وضعیت در نظر گرفته شده است و مقدار AIC برحسب تعداد پارامترها جریمه می‌شود، به نظر می‌رسد که برای تشخیص مدل مناسب، معیار بهتری باشد.

معیار AIC و تعیین تعداد پارامتر

برای آنکه بتوانیم معیاری بسازیم که به تعداد پارامترهای مدل حساس بوده و بتواند میزان مناسب بودن مدل را نشان دهد، از ترکیب تابع درستنمایی $$L(\theta)$$ و $$k$$ که بیانگر تعداد پارامترها است، استفاده می‌کنیم. ابتدا تابع درستنمایی را قرینه می‌کنیم تا بیشینه‌سازی تابع درستنمایی مشابه کمینه‌سازی تابع قرینه آن باشد. از آنجایی که توزیع مجانبی $$-2L(\theta)$$ نیز معلوم است از این عبارت برای تعیین معیار جدید استفاده می‌کنیم. از طرفی میزان جریمه را هم به شکل $$2k$$ در نظر می‌گیریم تا شدت جریمه را متناسب با دوبرابر تعداد پارامترها تعیین کنیم. در این صورت رابطه زیر را AIC می‌نامیم.

$$\large  AIC = 2k-2\ln (L(\theta_0))$$

منظور از $$\theta_0$$ نقطه‌ای از فضای پارامتری است که تابع درستنمایی (لگاریتم تابع درستنمایی) را حداکثر می‌کند. این مراحل محاسباتی AIC برای مدل $$m1$$ در کدهای زیر دیده می‌شود.

1LLm1 <- sum(dnorm(y, mean = predict(m1), sd = sqrt(sm1$dispersion), log = TRUE))
2-2*LLm1
3
4## [1] 251.2428

در انتها نیز مقدار $$2k$$ نیز اضافه می‌شود تا نتیجه AIC بدست آید.

1-2*LLm1 + 2*3
2
3## [1] 257.2428

از آنجایی که پارامترهای مدل عرض از مبدا $$a$$، شیب خط $$b$$ و البته واریانس جمله خطا است، تعداد پارامترها برابر با $$3$$ در نظر گرفته شده است. در ادامه برای مدل‌های $$m2$$ و $$m3$$ نیز مقدار AIC را محاسبه می‌کنیم.

1LLm2 <- sum(dnorm(y, mean = predict(m2), sd = sqrt(sm2$dispersion), log = TRUE))
2-2*LLm2 + 2*3
3
4## [1] 501.6118
5
6LLm3 <- sum(dnorm(y, mean = predict(m3), sd = sqrt(sm3$dispersion), log = TRUE))
7-2*LLm3 + 2*4
8
9## [1] 258.9686

مشخص است که برای مدل $$m1$$ مقدار AIC کوچکترین مقدار است. در نتیجه برحسب معیار AIC، این مدل به نظر مناسب‌تر می‌رسد.

نکته: البته برای محاسبه AIC می‌توانید از تابع کتابخانه stats به نام AIC استفاده کنید. کد زیر این کار را انجام می‌دهد. مشاهده می‌کنید که مقدارهای محاسبه شده توسط این تابع درست به مانند محاسباتی است که در کد قبلی مشاهده شد.

1> AIC(m1)
2[1] 257.2225
3> AIC(m2)
4[1] 501.5915
5> AIC(m3)
6[1] 258.9226

اصول پایه AIC

هنگام استفاده از معیار AIC باید نکات و اصول زیر را در نظر گرفت. در غیر اینصورت ممکن است در نتایج حاصل از آن دچار اشتباه شویم.

• معیار AIC، روشی نسبی برای تعیین مدل مناسب است. در این صورت محاسبه AIC برای یک مدل به تنهایی معنی ندارد و مقدار آن باید با AIC مدل‌های دیگر مقایسه شود.
• در بین مدل‌ها، کوچکترین مقدار AIC مدل مناسب را تعیین می‌کند.
• از معیار AIC برای انتخاب مدل‌ مناسب از بین مدل‌هایی که روی مجموعه داده ثابتی ایجاد شده‌اند باید استفاده کرد.
• اگر تعداد نمونه‌ها زیاد باشد، ممکن است معیار AIC‌ دچار مشکل شود. در این هنگام بهتر است از معیار AIC اصلاح شده که به نام AICc‌ معروف است، استفاده کنید.

اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزش‌هایی که در ادامه آمده‌اند نیز برایتان کاربردی خواهند بود.

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آموزش تخمین خطای طبقه بندی یا Classifier Error Estimation
• مجموعه آموزش‌های داده‌کاوی و یادگیری ماشین
• بیش برازش (Overfitting)، کم برازش (Underfitting) و برازش مناسب — مفهوم و شناسایی
• تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده

^^