زوایای مجاور و تعریف آنها در هندسه – به زبان ساده
۲۲۴۵۴
۱۴۰۱/۱۰/۳
۰ دقیقه
PDF
آموزش متنی جامع
امکان دانلود نسخه PDF
دو زاویه را مجاور (Adjacent) مینامیم هرگاه یک رأس و یک ضلع مشترک داشته باشند و با هم همپوشانی نداشته باشند.
فهرست مطالب این نوشته
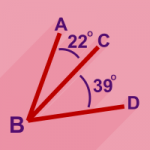
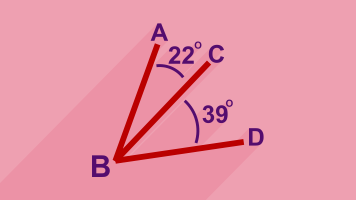
زاویه ABC مجاور زاویه CBD است، زیرا
- یک ضلع مشترک دارند. (خط CB)
- یک رأس مشترک دارند. (نقطه B)
کدامیک از زوایای زیر مجاورند؟
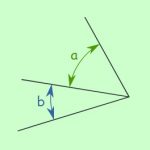
این دو زاویه مجاور هستند زیرا یک رأس و یک ضلع مشترک دارند.
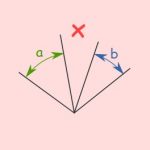
این دو زاویه مجاور نیستند زیرا فقط یک رأس مشترک دارند و ضلع مشترک ندارند.
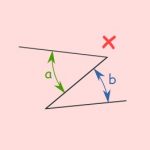
این دو زاویه مجاور نیستند، زیرا فقط یک ضلع مشترک دارند و رأس مشترک ندارند.
شرط عدم همپوشانی
باید توجه داشته باشید که علاوه بر شرط وجود یک رأس و ضلع مشترک، دو زاویه نباید همپوشانی داشته باشند.
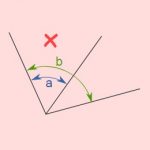
این دو زاویه مجاور نیستند، زیرا زاویه a و زاویه b همپوشانی دارند.
اگر پرسشی درباره این مطلب دارید، آن را با ما مطرح کنید.
PDF
مطالب مرتبط
همپوشانی یعنی چی ؟
با سلام خدمت شما؛
منظور از همپوشانی زاویهها در هندسه وضعیتی است که در آن دو یا چند زاویه دقیقا بر روی یکدیگر منطبق میشوند، به این شکل که راس مشترک دارند، اضلاع آنها روی یکدیگر قرار میگیرد و هیچکدام بخشی جدا از دیگری ندارد. برای مثال، اگر دو زاویه داشته باشیم که با انتقال و چرخاندن یکی از آنها بتوان آن را دقیقا روی دیگری قرار داد، میگوییم این دو زاویه همپوشانی دارند.
از همراهی شما با مجله فرادرس سپاسگزاریم.
محشر بود درک عالی داشت
عالیییی
عالی??
خوب بود
عالی بود
خوبه ولی معلم ما همه این شکل ها رو از اینجا کپی کرده توضیح داده و ما رو مجبور کرده بنویسیمشون
واقعا یک مثال در کلاس کافی نیست