نمونه گیری گیبز (Gibbs Sampling) و کاربردهای آن — به زبان ساده

در نظریه آمار بیز و استنباط بیزی، یکی از تکنیک‌های نمونه‌گیری به منظور استنباط پارامتر مجهول جامعه، «نمونه گیری گیبز» (Gibbs Sampling) است. نمونه گیری گیبز و کاربردهای آن در الگوریتم «زنجیره مارکف مونت کارلو» (MCMC) بسیار مشخص است بطوری که بوسیله آن، نمونه‌گیری به صورت دنباله‌ای از توزیع‌های چند متغیره امکان پذیر شده و برآورد پارامتر جامعه صورت می‌گیرد.

زمانی که نمونه‌گیری از یک توزیع به راحتی امکان پذیر نیست، روش نمونه گیری گیبز، این امکان را فراهم می‌آورد که بوسیله دنباله‌ای از نمونه‌ها براساس توزیع پیشین پارامتر جامعه، بتوانیم از توزیع پسین، نمونه استخراج کنیم. به این منظور به جای استفاده از «توزیع توام» (Joint Distribution) برای تولید داده، از «توزیع‌ حاشیه‌ای» (Marginal Distribution) و «توزیع شرطی» (Conditional Distribution) که نمونه‌گیری از آن‌ها ساده‌تر است، استفاده می‌شود تا بتوانیم پارامتر مجهول جامعه را برآورد کنیم. البته استفاده از نمونه گیری گیبز برای محاسبه انتگرال به شیوه مونت کارلو درست به مانند شبیه‌سازی مونت‌کارلو نیز موثر است.

از نمونه گیری گیبز برای استنباط آماری بخصوص استنباط بیزی استفاده می‌شود. برعکس «الگوریتم قطعی» (Deterministic Algorithm) مانند الگوریتم EM، الگوریتم نمونه گیری گیبز یک «الگوریتم تصادفی» (Randomized Algorithm) است زیرا براساس اعداد و دنباله‌ای از نمونه‌های تصادفی عمل می‌کند.

نمونه گیری گیبز (Gibbs Sampling) و کاربردهای آن

شیوه و روش نمونه گیری گیبز به افتخار فعالیت‌ها و کارهایی که دانشمند و فیزیکدان آمریکایی «جوسیا ویلارد گیبز» (Josiah Willard Gibbs) در حوزه مکانیک آماری انجام داده به این نام خوانده می‌شود. او اولین با واژه «مکانیک آماری» (Statistical Mechanic) را به کار برد و مفاهیم آن را در سال ۱۹۰۲ توسعه دارد. البته بعدها استنباط آماری توسط دو برادر به نام‌های «استوارت» و «دونالد گمان» (Stuart - Donald Geman) در سال ۱۹۸۴ ایده‌های او را بسط داده و به صورت یک شاخه از مکانیک مدرن معرفی کردند. به نظر می‌رسد این ایده تقریبا حدود ۸۰ سال بعد از در گذشت جوسیا گبیز بسط و مورد استفاده قرار گرفت.

فیلم آموزش تحلیل های بیزی با نرم افزار وین باگز WinBUGS در فرادرس

کلیک کنید

نمونه‌گیری گیبز را در حالت ساده می‌توان حالت خاصی از الگوریتم متروپولیس-هستنینگز (Metropolis-Hastings Algorithm) دانست. از کاربردهای مهم نمونه‌گیری گیبز می‌توان به تهیه داده و نمونه از یک توزیع چند متغیره پیچیده و با شکل نامخشص براساس توزیع شرطی و توزیع حاشیه‌ای نام برد. البته فرض بر این است که توزیع شرطی و توزیع‌های حاشیه‌ای مشخص و نحوه تهیه نمونه از آن‌ها نسبت به توزیع توام ساده است. می‌توان نشان داد که دنباله نمونه‌های ایجاد شده توسط الگوریتم نمونه گیری گیبز یک «زنجیره مارکف» (Markov Chain) ایجاد می‌کنند.

به کمک قضیه بیز می‌توان نمونه گیری گیبز را به شکلی مرتبط با توزیع پسین در شبکه بیزی (Bayesian Network) دانست زیرا شبکه‌های بیزی به صورت مجموعه‌ای از توزیع‌های شرطی، مشخص و معرفی می‌شوند.

پیش‌زمینه ریاضیاتی

در این قسمت به بررسی مفاهیم اولیه و ریاضیاتی برای نمونه گیری گیبز خواهیم پرداخت. البته همانطور که قبلا اشاره شد، نمونه گیری گیبز به قضیه بیز و استفاده از آن برای پیدا کردن توزیع توام نمونه تصادفی برحسب توزیع شرطی و توزیع حاشیه‌ای تکیه دارد. به این ترتیب برای مشخص شدن این ارتباط در این بخش به معرفی توزیع شرطی و توزیع حاشیه‌ای و ارتباطشان با توزیع توام خواهیم پرداخت.

فرض کنید یک نمونه تصادفی به صورت $$X$$ از توزیعی که به پارامتر $$d$$ بُعدی  $$\theta \in Theta$$ وابسته است، تهیه شده است. از طرفی می‌دانیم توزیع پیشین برای بردار پارامتر $$\theta$$ به صورت $$g(\theta_1, \theta_2, \ldots, \theta_n)$$ است. معمولا اگر مقدار $$n$$‌ بزرگ باشد، محاسبه توزیع حاشیه‌ای برای هر $$\theta$$ کار مشکلی خواهد بود، زیرا احتیاج به محاسبه یک انتگرال $$n-1$$گانه داریم. راه جایگزین برای این کار، محاسبه توزیع حاشیه‌ای $$\theta_i$$ براساس انجام گام‌های متوالی زیر است. مشخص است که در اینجا $$n$$ بُعد مسئله یا تعداد پارامترها را نشان می‌دهد.

1. یک اندیس تصادفی مثل $$j$$ را از بین اعداد ۱ تا $$n$$ انتخاب می‌کنیم. البته بعد خواهیم دید که بهتر است این اندیس از ۱ شروع شود. به این معنی که از اولین پارامتر شروع می‌کنیم.
2. براساس احتمال حاصل از توزیع توام $$g(\theta _{1},\ldots ,\theta _{{j-1}},\,\cdot \,,\theta _{{j+1}},\ldots ,\theta _{n})$$ یک مقدار برای $$\theta_j$$ انتخاب می‌کنیم.

به این ترتیب با تکرار این کار می‌توانیم تابع احتمال حاشیه‌ای برای هر $$\theta$$ استخراج کنیم. این کار درست به مانند به کارگیری «زنجیره مارکف وارون‌پذیر» (Reversible Markov Chain) است.

نکته: یک زنجیره مارکف را وارون‌پذیر می‌نامند اگر رابطه زیر برقرار باشد.

$$ \large {\displaystyle \pi _{i}\Pr(X_{n+1}=j\mid X_{n}=i)=\pi _{j}\Pr(X_{n+1}=i\mid X_{n}=j)}$$

رابطه بالا نشان می‌دهد که اگر زنجیره مارکف، یکنواخت در زمان باشد، احتمال تغییر حالت از $$i$$ به $$j$$ متناسب با تغییر حالت از $$j$$ به $$i$$ است. این نسبت براساس تابع احتمال $$\pi$$ مشخص می‌شود.

نمونه گیری گبیز (Gibbs Sampling)

فرض کنید احتیاج به یک نمونه تصادفی با اندازه $$k$$ به صورت $${\mathbf {X}}=(x_{1},\dots ,x_{n})$$ از توزیع توام $${\displaystyle p(x_{1},\dots ,x_{n})}$$ داریم. در نظر بگیرید که $${\displaystyle \mathbf {X} ^{(i)}=\left(x_{1}^{(i)},\dots ,x_{n}^{(i)}\right)}$$ نمونه تصادفی در مرحله $$i$$ام است. به این ترتیب گام‌های تولید نمونه تصادفی در نمونه‌گیری گبیز به صورت زیر خواهد بود.

فیلم آموزش کنترل کیفیت آماری در فرادرس

کلیک کنید

1- در اولین گام با مقدار اولیه و اختیاری برای $$X{(۱)}$$ آغاز می‌کنیم.

۲- در گام بعدی نمونه جدیدی به نام $$X{(i+1)}$$ ایجاد خواهیم کرد. از آنجایی که $$X^{(i+1)}$$ یک بردار به صورت $$ {\displaystyle \mathbf {X} ^{(i+1)}=\left(x_{1}^{(i+1)},x_{2}^{(i+1)},\dots ,x_{n}^{(i+1)}\right)}$$ است، تابع احتمال برای انتخاب نمونه برای هر یک از مولفه‌ها مثلا $$x_j^{(i+1)}$$ را بوسیله تابع توزیع شرطی آن مولفه برحسب دیگر مولفه‌ها در نظر می‌گیریم. این احتمال یا توزیع شرطی را به صورت زیر نمایش می‌دهیم.

$$ \large {\displaystyle p\left(x_{j}^{(i+1)}|x_{1}^{(i+1)},\dots ,x_{j-1}^{(i+1)},x_{j+1}^{(i)},\dots ,x_{n}^{(i)}\right)}$$

نکته: باید توجه داشت که ما از مقدار $$(j+1)$$امین مولفه در نمونه $$i$$ام استفاده کرده‌ایم. از طرفی هم برای نمونه‌گیری نیز از مولفه اول کار را آغاز کرده‌ایم. به اندیس‌های بالا و پایین جملات اولیه و همچنین جملاتی که در آخر رابطه بالا دیده می‌شوند دقت کنید. نمونه‌های استفاده شده برای محاسبه احتمال شرطی برای مولفه $$j$$ شامل نمونه $$i+1$$ام برحسب مولفه اول تا  $$j-1$$ به همراه مولفه‌های $$j+1$$ تا $$n$$ نمونه‌ $$i$$ام است. این امر مرحله‌ای بودن و تکرار مراحل در نمونه گیری گبیز را به خوبی نشان می‌دهد. همچنین مشخص است که از بیشترین اطلاعات برای تعیین توزیع و یا تولید نمونه تصادفی در گام بعدی استفاده شده است. به این ترتیب برای نمونه $$i+1$$ام مولفه‌های 1 تا $$n$$ تولید می‌شود.

۳- گام ۲ را به تعداد $$k$$ بار (تعداد نمونه‌‌ها) تکرار می‌کنیم.

رابطه بین توزیع شرطی و توزیع توام

توزیع شرطی یک متغیر تصادفی برحسب متغیرهای دیگر به شکل زیر نوشته می‌شود.

$$\large {\displaystyle p(x_{j}\mid x_{1},\dots ,x_{j-1},x_{j+1},\dots ,x_{n})={\frac {p(x_{1},\dots ,x_{n})}{p(x_{1},\dots ,x_{j-1},x_{j+1},\dots ,x_{n})}}\propto p(x_{1},\dots ,x_{n})}$$

مشخص است که صورت کسر شامل توزیع توام همه نمونه‌های تصادفی است. همچنین در مخرج کسر نیز توزیع توام بدون در نظر گرفتن نمونه $$j$$ نوشته شده است. به این ترتیب به نظر می‌رسد که توزیع شرطی یک نمونه تصادفی، متناسب با توزیع توام نمونه تصادفی است. پس مشخص است که توزیع شرطی متغیر تصادفی $$x_j$$ با توجه به صورت کسر فقط به توزیع توام نمونه‌ها بستگی دارد که برای همه $$x_j$$‌ها یکسان است. این امر نشان می‌دهد که می‌توان توزیع توام را بر حسب توزیع شرطی یک نمونه تصادفی و توزیع توام بقیه نمونه‌ها تولید کرد. مخرج کسر را عامل نرمال‌سازی می‌نامند. بنابراین می‌توان یکی از کارهای زیر را انجام داد.

• اگر توزیع متغیر تصادفی گسسته باشد، توزیع احتمال نمونه‌ تصادفی به ازائ همه حالت‌های ممکن برای $$x_j$$ را محاسبه کرد.
• اگر توزیع متغیر تصادفی پیوسته و معلوم باشد، عامل نرمال سازی در محاسبه توزیع توام نیز معلوم خواهد بود.
• در حالت‌هایی غیر از دو وضعیت بالا، مقدار فاکتور نرمال سازی که باعث تبدیل تابع تولید شده به تابع چگالی است، را می‌توان نادیده گرفت و براساس بقیه عوامل، توزیع توام را محاسبه کرد.

استنابط به کمک نمونه‌گیری گبیز

نمونه گیبز معمولا برای استنتاج آماری استفاده می‌شود. برای مثال می‌توان از نمونه‌گیری گیبز برای برآورد پارامتر توزیع پواسن ($$\lambda$$) که بیانگر متوسط تعداد افرادی است که احتمالا در یک فروشگاه خاص در یک روز خاص خرید می‌کنند استفاده کرد. ایده اصلی در این زمینه آن است که داده‌های مشاهده شده و توزیع شرطی با یکدیگر آمیخته شده تا برای تولید نمونه تصادفی از توزیع توام به کار گرفته شوند. در هر بار تکرار فرآیند نمونه گیری گیبز، توزیع متغیرهای باقی‌مانده همان توزیع پیشین و شرطی شده برحسب مشاهدات است.

به این ترتیب نزدیکترین مقدار به پارامتر (مقداری با بیشترین فراوانی یا همان نما) می‌تواند به عنوان مقدار برآورد پارامتر در نظر گرفته شود. این درست به مانند برآورد حداکثر احتمال پسین در استنباط آماری برای پارامتر مجهول جامعه است. اگر از میانگین (امید ریاضی) مقدارهای حاصل از نمونه‌های تولید شده برای پارامتر مجهول در نمونه‌گیری گیبز استفاده کنیم، معادل برآوردگر بیز در مباحث استنباط بیزی است. به این ترتیب از اطلاعات اضافه‌ای که داده‌های قبلی به همراه دارند، استفاده کرده‌ایم در حالیکه اگر از الگوریتم EM کمک بگیریم چنین امکانی برایمان وجود ندارد.

برای مثال یک توزیع تک نمایی (Unimodal) را در نظر بگیرید. معمولا در چنین توزیعی با شرط وجود تقارن، میانگین و نما (Mode) تقریبا با یکدیگر برابر هستند. ولی اگر میزان «چولگی» (Skewness) در یک جهت زیاد باشد، میانگین در جهت چولگی تمایل پیدا کرده و از نما دور می‌شود. به این ترتیب احتمال مشاهده مقادیر در جهت چولگی نسبت به حالت تقارن بیشتر می‌شود. گاهی اوقات می‌توان با استفاده از نمونه‌گیری گیبز مقادیر مرتبط با یک مدل خطی (یعنی تغییرات رگرسیون خطی) را بررسی کرد. برای مثال، رگرسیون probit را می‌توان برمبنای نمونه‌گیری گبیز برای تعیین احتمال انتخاب یک داده باینری  (مثلا بله / خیر) به عنوان متغیر وابسته با متغیرهایی مستقل به همراه جمله خطا که توزیع آن نرمال در نظر گرفته شده است به کار برد.

اشکالات نمونه‌گیری گیبز

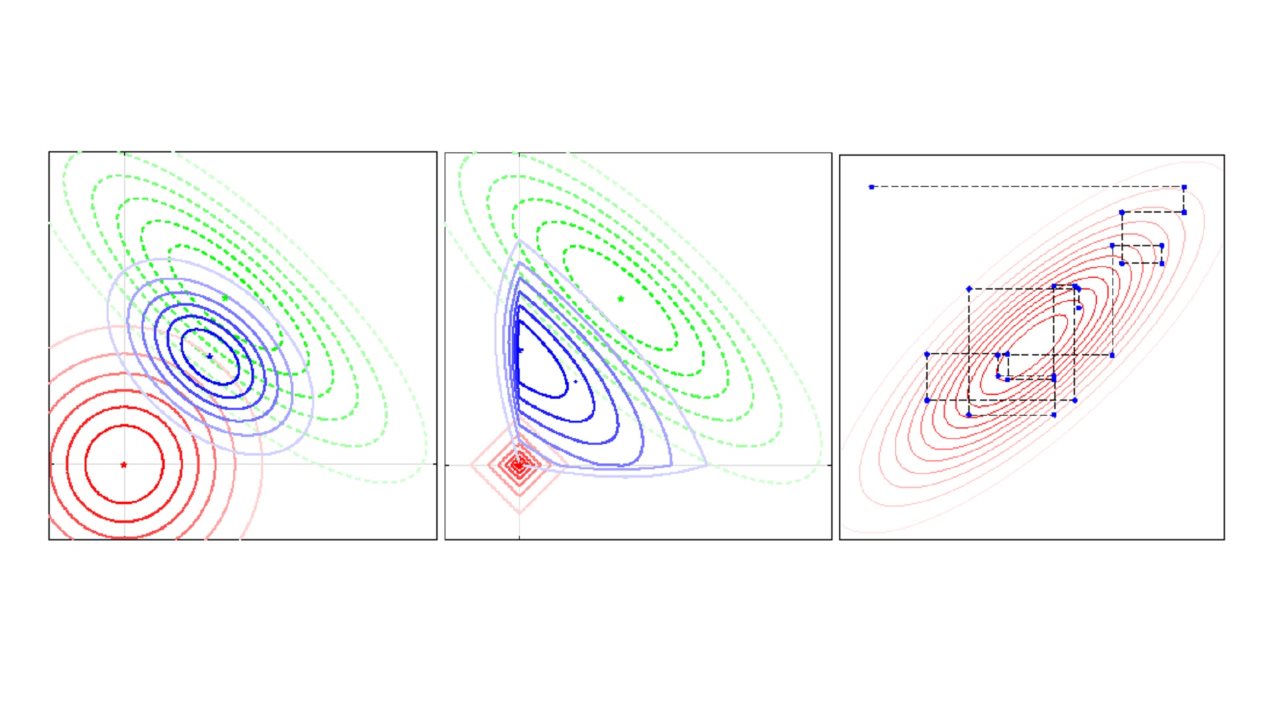
در دو حالت، ممکن است نمونه‌گیری گیبز به شکست منجر شود. اولین وضعیت، زمانی است که داده‌ها در محل یا مقدارهای خاصی، چگال‌تر (متمرکز) باشند و تشکیل توزیع احتمال به صورت جزیره‌هایی منفصل با میزان احتمال بالا را بدهند. برای مثال توزیعی را در نظر بگیرید که توسط یک بردار دو بعدی از مقدارهای دو دویی تشکیل شده است، بطوری که در نقطه $$(0,0)$$ و $$(1,1)$$ میزان جرم احتمال $$\dfrac{1}{2}$$ است و در بقیه نقاط یعنی $$(0,1)$$ و $$(1,0)$$ جرم احتمال صفر است. به این ترتیب نمونه‌گیری گیبز در بین دو نقطه با بیشترین جرم احتمال متوقف شده و هرگز نقاط دیگر از مقدارهای توزیع را تولید نخواهد کرد. این حالت بخصوص زمانی که دو مقدار یا مولفه از بردارها کاملا به یکدیگر وابسته باشند نیز رخ می‌دهد.

در حالت دوم، همه نقاط دارای احتمال مثبت هستند ولی یک نقطه با جرم احتمال زیاد وجود دارد. برای مثال فرض کنید که یک بردار ۱۰۰ مولفه‌ای با مقدار مولفه‌هایی برابر با صفر دارید که با احتمال $$\dfrac{1}{2}$$ رخ می‌دهند. به این ترتیب اگر نقاط دیگر دارای جرم احتمال یکسان باشند، میزان احتمال برای بردارهای دیگر برابر با رابطه زیر است.

$$ \large \dfrac{1}{2(2^{100}-1)}$$

به این ترتیب اگر لازم باشد که احتمال مشاهده بردار صفر را برآورد کنیم، کافی است ۱۰۰ تا ۱۰۰۰ داده تولید کرده و احتمال را برآورد کنیم. در حالیکه اگر بخواهیم برای بردارهایی دیگر میزان احتمال را برآورد کنیم احتیاج به حداقل یک نمونه به اندازه $$s^{100}$$‌ داریم که عملا هیچ رایانه‌ای امکان محاسبات این چنینی را ندارد.

تولید نمونه‌ از توزیع نرمال دو متغیره با روش نمونه‌گیری گیبز

فرض کنید می‌خواهیم از یک توزیع نرمال دو متغیره نمونه تولید کنیم. پارامترهای این توزیع را به صورت زیر در نظر می‌گیریم.

$$\large  \mu = [\mu_1,\mu_2]= [0, 0]$$

که بردار میانگین توزیع نامیده می‌شود و همچنین ماتریس زیر را هم در نظر بگیرید که ماتریس کوواریانس (ماتریس ضریب همبستگی) با میزان ضریب همبستگی 0.8 بین دو متغیر را نشان می‌دهد.

فیلم آموزش فرآیند آماری در کنترل کیفیت آماری (رایگان) در فرادرس

کلیک کنید

به نظر می‌رسد که این متغیر تصادفی دارای توزیع نرمال دو متغیره استاندارد است زیرا میانگین‌ها صفر و واریانس‌ها نیز برابر با ۱ هستند.

$$\large \Sigma = \begin{bmatrix} 1 & \rho_{12} \\ \rho_{21} & 1\end{bmatrix} = \begin{bmatrix} 1 & 0.8 \\ 0.8 & 1\end{bmatrix}$$

به منظور تهیه نمونه از این توزیع، از نمونه‌گیری گیبز استفاده می‌کنیم زیرا می‌دانیم توزیع شرطی و توزیع حاشیه‌ای چنین متغیر تصادفی نیز نرمال تک متغیره خواهند بود و نمونه‌گیری از آن به سادگی امکان‌پذیر است. به این ترتیب توزیع‌های شرطی یک بُعد برحسب بُعد دیگر را به صورت زیر نشان می‌دهیم.

$$\large p(x_1 | x_2^{(i)}) $$

که توزیع احتمال شرطی مولفه‌ اول برحسب مولفه دوم را نشان می‌دهد. همچنین توزیع زیر احتمال شرطی مولفه دوم برحسب مولفه اول را به صورت زیر مشخص می‌کنیم.

$$\large p(x_۲ | x_۱^{(i)}) $$

در اینجا مشخص است که در گام $$i+1$$ام از نمونه گام $$i$$ام استفاده کرده‌ایم. با استفاده از اطلاعاتی که از توزیع شرطی و نحوه محاسبه آن داریم می‌توانیم، رابطه‌های زیر را مشخص کنیم. ابتدا توزیع شرطی متغیر $$x_1$$ را تعیین می‌کنیم.

$$\large p(x_1 | x_2^{(i)}) = \mathcal N(\mu_1 + \rho_{21}(x_2^{(i)} - \mu_2),\sqrt{1-\rho_{21}^2})$$

به این ترتیب با معلوم بودن توزیع $$x_1$$ در گام $$i+1$$ام توزیع $$x_2$$ را بدست می‌آوریم.

$$\large p(x_2 | x_1^{(i+1)})=\mathcal N(\mu_2 + \rho_{12}(x_1^{(i+1)}-\mu_1),\sqrt{1-\rho_{12}^2}),$$

واضح است که هر دو توزیع شرطی، نرمال یک متغیره هستند. به میانگین و واریانس هر یک از توزیع‌ها توجه کنید. مشخص است که برای مثال میانگین توزیع شرطی $$x_1$$ برحسب $$x_2$$ به صورت ترکیبی از میانگین توزیع بُعد اول و دوم و همچنین ضریب همبستگی و مقدار متغیر در بُعد دوم است. یعنی داده‌های جمع‌آوری شده قبلی در بُعد دوم برای اصلاح میانگین متغیر تصادفی در بُعد اول در مرحله $$i+1$$ام به کار رفته است. به این ترتیب امید ریاضی و واریانس توزیع نرمال در بُعد اول به صورت زیر خواهد بود.

$$\large E(x_۱|x_۲)=\mu_۱ + \rho_{۲۱}(x_۲^{(i)}-\mu_۲)$$

$$\large V(x_1|x_2)=\sqrt{1-\rho^2_{21}}$$

به همین شکل نیز رابطه‌ای مانند زیر را برای میانگین و واریانس شرطی بُعد دوم خواهیم داشت.

$$\large E(x_۲|x_۱)=\mu_2 + \rho_{12}(x_1^{(i+1)}-\mu_1)$$

$$\large V(x_۲|x_۱)=\sqrt{1-\rho^2_{1۲}}$$

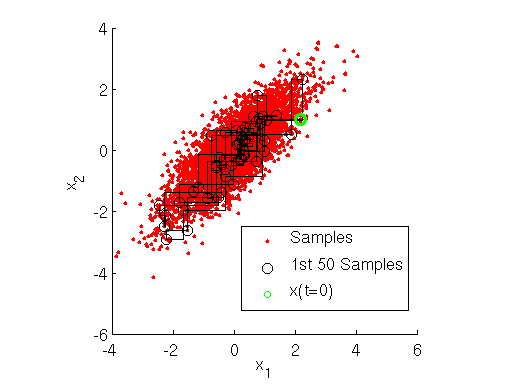
قطعه کدی که در ادامه مشاهده می‌کنید به زبان برنامه‌نویسی MATLAB نوشته شده و برای ایجاد نمونه‌‌ای ۵۰۰۰ تایی از توزیع نرمال دو متغیره بوسیله نمونه‌گیری گبیز  به کار می‌رود. در متغیر nSamples تعداد نمونه‌ها مشخص شده همچنین بردار میانگین در mu و ضریب همبستگی نیز در (rho(1 و (rho(2‌ مشخص شده‌اند تا بتوان ماتریس کوواریانس یا همبستگی را تشکیل داد. بازه تولید نمونه‌ها نیز در گام اول از نقطه $$[-3,-3]$$ تا نقطه $$[3,3]$$ انتخاب شده است.

1% EXAMPLE: GIBBS SAMPLER FOR BIVARIATE NORMAL
2rand('seed' ,12345);
3nSamples = 5000;
4 
5mu = [0 0]; % TARGET MEAN
6rho(1) = 0.8; % rho_21
7rho(2) = 0.8; % rho_12
8 
9% INITIALIZE THE GIBBS SAMPLER
10propSigma = 1; % PROPOSAL VARIANCE
11minn = [-3 -3];
12maxx = [3 3];
13 
14% INITIALIZE SAMPLES
15x = zeros(nSamples,2);
16x(1,1) = unifrnd(minn(1), maxx(1));
17x(1,2) = unifrnd(minn(2), maxx(2));
18 
19dims = 1:2; % INDEX INTO EACH DIMENSION
20 
21% RUN GIBBS SAMPLER
22t = 1;
23while t < nSamples
24    t = t + 1;
25    T = [t-1,t];
26    for iD = 1:2 % LOOP OVER DIMENSIONS
27        % UPDATE SAMPLES
28        nIx = dims~=iD; % *NOT* THE CURRENT DIMENSION
29        % CONDITIONAL MEAN
30        muCond = mu(iD) + rho(iD)*(x(T(iD),nIx)-mu(nIx));
31        % CONDITIONAL VARIANCE
32        varCond = sqrt(1-rho(iD)^2);
33        % DRAW FROM CONDITIONAL
34        x(t,iD) = normrnd(muCond,varCond);
35    end
36end
37 
38% DISPLAY SAMPLING DYNAMICS
39figure;
40h1 = scatter(x(:,1),x(:,2),'r.');
41 
42% CONDITIONAL STEPS/SAMPLES
43hold on;
44for t = 1:50
45    plot([x(t,1),x(t+1,1)],[x(t,2),x(t,2)],'k-');
46    plot([x(t+1,1),x(t+1,1)],[x(t,2),x(t+1,2)],'k-');
47    h2 = plot(x(t+1,1),x(t+1,2),'ko');
48end
49 
50h3 = scatter(x(1,1),x(1,2),'go','Linewidth',3);
51legend([h1,h2,h3],{'Samples','1st 50 Samples','x(t=0)'},'Location','Northwest')
52hold off;
53xlabel('x_1');
54ylabel('x_2');
55axis square

پس از اجرای این برنامه علاوه بر ایجاد نمونه‌های دو بعدی از این توزیع در متغیر $$x$$ نموداری نیز از این توزیع براساس نمونه‌های تولید شده ترسیم می‌شود. نقطه‌های حاصل از تولید این نمونه‌ها در نمودار زیر با دایره‌های قرمز رنگ مشخص شده‌اند. در انتهای این برنامه برای پنجاه نقطه از نقاط تولید شده، مراحل جایگزینی و انتخاب در نمونه گیری گیبز به صورت خطوط سیاه رنگ دیده می‌شود.

نرم‌افزارهای تحلیلی با نمونه‌گیری گیبز

در زمینه استنباط و تحلیل‌های بیزی نرم‌افزارهای مختلفی با تکیه بر نمونه‌گیری گیبز ایجاد و مورد استفاده قرار گرفته است. برای مثال WinBUGS و OpenBUGS براساس تحلیل بیزی و استفاده از نمونه‌گیری گیبز در زنجیره مارکف مونت‌کارلو، استنباط آماری و برآورد پارامترها را انجام می‌دهند.  همچنین نرم‌افزار  JAGS که اختصار عبارت (Just another Gibbs Sampler) به معنی یک «نمونه‌ گیری گیبز دیگر» است، به عنوان یک برنامه متن باز برای تحلیل‌های سلسله مراتبی بیزی با استفاده از زنجیره مارکف مونت‌کارلو قابل استفاده است.

از دیگر نرم‌افزارها در این زمینه می‌توان به Church و PyMC3 که در پایتون قابل استفاده است، اشاره کرد. همچنین IA2RMS که مخفف (Independent Doubly Adaptive Rejection Metropolis Sampling) است، یک بسته برای متلب (Matlab) برای نمونه‌گیری براساس چگالی‌های شرطی با تکیه بر نمونه‌گیری گیبز محسوب می‌شود.

اگر مطلب بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار و احتمالات
• آموزش مقدماتی آمار بیزی
• مجموعه آموزش‌های برنامه‌‌نویسی R و نرم‌ افزار RStudio
• دسته‌ بند بیز ساده (Naive Bayes Classifiers) — مفاهیم اولیه و کاربردها
• یادگیری ماشین به زبان قضیه بیز، بی نظمی شانون و فلسفه
• احتمال پسین (Posterior Probability) و احتمال پیشین (Prior Probability) — به زبان ساده

^^