ممان اینرسی نیم دایره – به زبان ساده

ممان اینرسی یا گشتاور دوم سطح نیم دایره، کمیتی است که نحوه توزیع نقاط تشکیل‌دهنده مقطع‌های نیم‌دایره‌ای نسبت به یک محور مشخص را نمایش می‌دهد. این کمیت، به عنوان معیاری برای ارزیابی رفتار المان‌های دارای مقطع نیم‌دایره‌ای در برابر بارهای خمشی مورد استفاده قرار می‌گیرد. هنگام بحث راجع به مقاومت اجسام در برابر بارهای مختلف، اولین نکته‌ای که به ذهن اغلب افراد می‌رسد، جنس ماده مورد استفاده است. با وجود تاثیر بسزای جنس مواد در مقاومت مکانیکی، شکل سطح مقطع نیز در بهینه‌سازی این مقاومت تاثیر می‌گذارد. به عنوان مثال، اجسام دارای مقاطع دایره‌ای و مستطیلی، مقاومت خوبی در برابر خمش و پیچش از خود به نمایش می‌گذارند. در این مقاله، به معرفی فرمول‌های ممان اینرسی نیم دایره و دیگر شکل‌های مرتبط با آن نظیر دایره، ربع دایره و قطاع دایره می‌پردازیم.

ممان اینرسی مقطع چیست ؟

ممان اینرسی یا گشتاور دوم سطح، یکی از مشخصات هندسی مقاطع دوبعدی است که توزیع ماده نسبت به یک محور مشخص را نمایش می‌دهد. به عنوان مثال، نحوه توزیع نقاط یک مقطع مستطیلی را برای دو حالت زیر در نظر بگیرید.

در هر یک از این حالت‌ها، توزیع نقاط نسبت به محورهای مبنا متفاوت است.

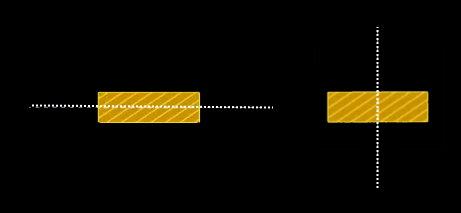
در شکل سمت راست، مجموع نقاط مستطیل در فاصله بیشتری نسبت به محور مبنا قرار دارند. در حالیکه در شکل سمت چپ، مجموع نقاط مستطیل، به محور مبنا نزدیک‌تر هستند. اگر هر یک از این مقاطع در راستای عمود بر محور مبنا، تحت بارگذاری قرار گیرند، مقاومت آن‌ها در برابر تنش‌های خمشی و پیچشی متفاوت خواهد بود در صورتیکه مساحت هر دوی آن‌ها یکسان است.

گشتاور دوم سطح، معیاری است که درک رفتار مقاطع تحت بارگذاری را بر اساس شکل آن‌ها کمی‌سازی می‌کند. فرمول کلی این کمیت به صورت زیر نوشته می‌شود:

$$ I _ x = \int \int _ { A } { y ^ ۲ dA } $$

$$
I _ x = \int \int _ { A } { y ^ ۲ d x d y }
$$

$$ I _ y = \int \int _ { A } { x ^ ۲ dA } $$

$$
I _ y = \int \int _ { A } { x ^ ۲ d x d y }
$$

• I_x: گشتاور دوم سطح دایره‌ای نسبت به محور مرکزی x
• y: فاصله عمودی نقاط تا محور مرکزی x
• I_y: گشتاور دوم سطح دایره‌ای نسبت به محور مرکزی y
• x: فاصله عمودی نقاط تا محور مرکزی y
• A: مساحت سطح
• dA: مقدار دیفرانسیلی مساحت سطح
• dx: اندازه دیفرانسیلی هر المان سطح در راستای x
• dy: اندازه دیفرانسیلی هر المان سطح در راستای y

ممان اینرسی سطح، با حرف انگلیسی I نمایش داده می‌شود. اندیس این حرف، بیانگر راستای محور مبنا است. به عنوان مثال، در فرمول بالا، I_x، نشان‌دهنده ممان اینرسی سطح نسبت به محور x (معمولا محور افقی گذرنده از مرکزی هندسی مقطع) است. در فرمول گشتاور دوم سطح، از مربع فاصله نقاط تا محور مبنا (y برای I_x یا x برای I_y)، بر روی تمام سطح (A)، انتگرال دوگانه گرفته می‌شود. یکای گشتاور دوم سطح، طول به توان چهار (میلی‌متر به توان چهار، سانتی‌متر به توان چهار، اینچ به توان چهار، فوت به توان چهار و غیره) است. در بخش بعدی، به معرفی فرمول ممان اینرسی نیم دایره و اثبات این فرمول از روی رابطه کلی ممان اینرسی سطح می‌پردازیم.

ممان اینرسی نیم دایره چگونه بدست می آید ؟

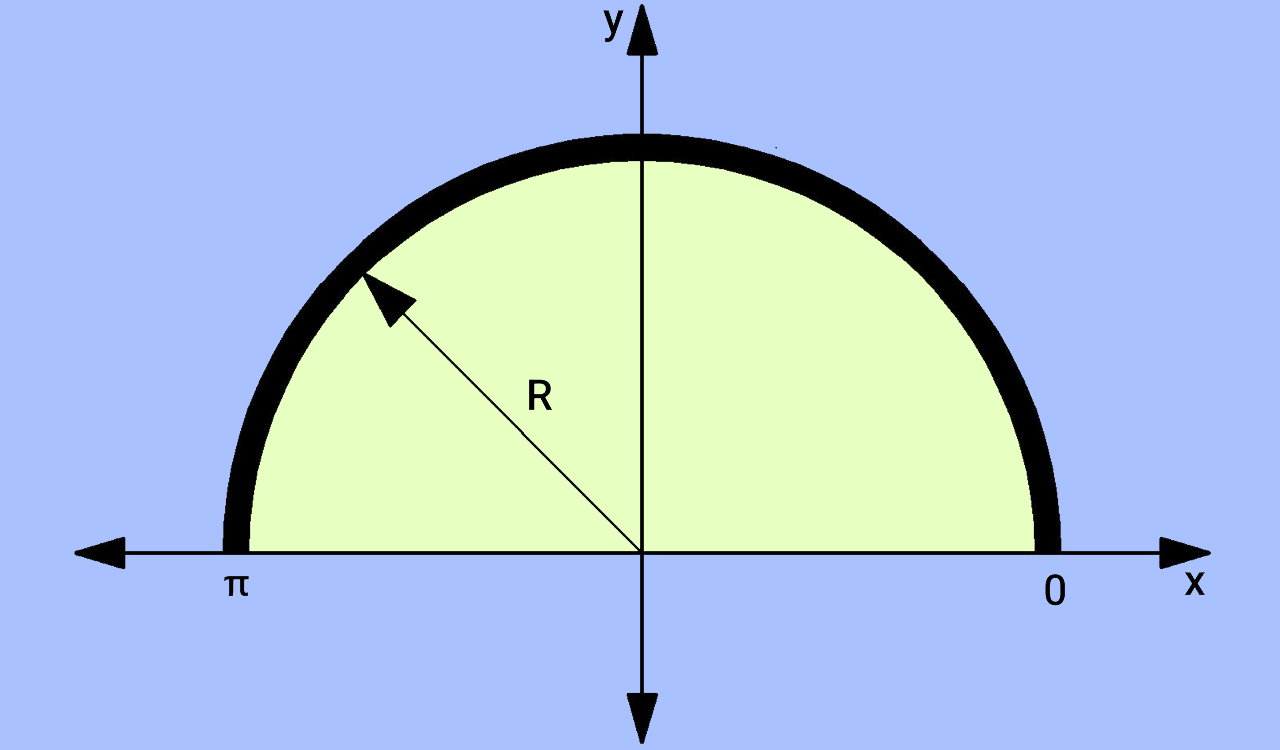
یک مقطع نیم‌دایره‌ای به شعاع r را مطابق با تصویر زیر در نظر بگیرید. این مقطع، در دستگاه مختصات x-y نمایش داده شده است.

محورهای x و y، از مرکز هندسی نیم‌دایره عبور می‌کنند.

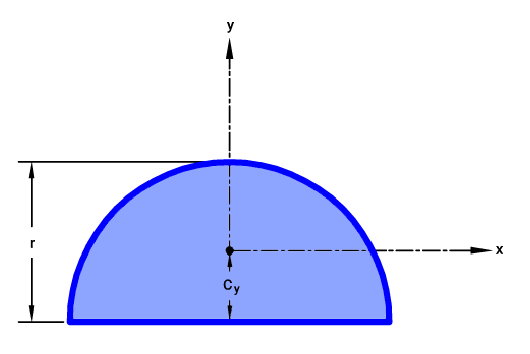
اگر محور مرکزی x را به عنوان محور مبنای محاسبه گشتاور دوم سطح انتخاب کنیم، فرمول ممان اینرسی نیم دایره توپر به صورت زیر نوشته می‌شود:

$$ I _ x = \left ( \frac { \pi }{ ۸ } - \frac { ۸ }{ ۹ \pi } \right ) r ^ ۴ $$

• I_x: گشتاور دوم سطح نیم دایره نسبت به محور مرکزی x
• r: شعاع نیم‌دایره

در صورت انتخاب محور مرکزی y به عنوان محور مبنای محاسبه گشتاور دوم سطح، فرمول ممان اینرسی نیم دایره توپر به شکل زیر درمی‌آید:

$$ I _ y = \frac { \pi r ^ ۴}{ ۸ } $$

• I_y: گشتاور دوم سطح نیم دایره نسبت به محور مرکزی y
• r: شعاع نیم‌دایره

مثال ۱: محاسبه ممان اینرسی سطح نیم دایره ای

ممان اینرسی یک نیم‌دایره توپر به شعاع ۹ سانتی‌متر را به دست بیاورید. عدد پی را برابر با ۳/۱۴ در نظر بگیرید.

برای به دست آوردن ممان اینرسی نیم دایره، ابتدا فرمول‌های آن و مقادیر معلوم را می‌نویسیم:

$$ I _ x = \left ( \frac { \pi }{ ۸ } - \frac { ۸ }{ ۹ \pi } \right ) r ^ ۴ $$

$$ I _ y = \frac { \pi r ^ ۴}{ ۸ } $$

• I_x: گشتاور دوم سطح نیم دایره نسبت به محور مرکزی x
• I_y: گشتاور دوم سطح نیم دایره نسبت به محور مرکزی y
• r: شعاع نیم‌دایره برابر با ۹ سانتی‌متر

برای ممان اینرسی مقطع حول محور مرکزی x داریم:

$$
I _ x = \left ( \frac { \pi }{ ۸ } - \frac { ۸ }{ ۹ \pi } \right ) \times ۹ ^ ۴
$$

$$
I _ x = \left ( \frac { \pi }{ ۸ } - \frac { ۸ }{ ۹ \pi } \right ) \times ۶۵۶۱
$$

$$
I _ x = \frac { \pi \times ۶۵۶۱ }{ ۸ } - \frac { ۸ \times ۶۵۶۱ }{ ۹ \pi }
$$

$$
I _ x = \frac { ۳/۱۴ \times ۶۵۶۱ }{ ۸ } - \frac { ۸ \times ۶۵۶۱ }{ ۹ \times ۳/۱۴ }
$$

$$
I _ x = \frac { ۲۰۶۰۱/۵۴ }{ ۸ } - \frac { ۵۲۴۸۸ }{ ۲۸/۲۶ }
$$

$$
I _ x = ۲۵۷۵/۱۹ - ۱۸۵۷/۳۲
$$

$$
I _ x = ۷۱۷/۸۷
$$

برای ممان اینرسی مقطع حول محور مرکزی y نیز داریم:

$$
I _ y = \frac { ۳/۱۴ \times ۹ ^ ۴}{ ۸ }
$$

$$
I _ y = \frac { ۳/۱۴ \times ۶۵۶۱ }{ ۸ }
$$

$$
I _ y = \frac { ۲۰۶۰۱/۵۴ }{ ۸ }
$$

$$
I _ y = ۲۵۷۵/۱۹
$$

در نتیجه، ممان اینرسی نیم دایره حول x برابر با ۷۱۷/۸۷ سانتی‌متر به توان چهار و حول محور y‌ برابر با ۲۵۷۵/۱۹ سانتی‌متر به توان چهار است. این اعداد، بیانگر پراکندگی بیشتر نقاط نیم‌دایره نسبت به محور مرکزی y در مقایسه با محور مرکزی x‌ هستند. به عبارت دیگر، اگر این مقطع، در راستای عمود بر محور y تحت بارگذاری قرار گیرد، مقاومت خمشی بیشتری را از خود به نمایش می‌گذارد.

ممان اینرسی قطبی نیم دایره

گشتاور قطبی یا ممان اینرسی قطبی، کمیت هندسی دیگری است که به عنوان پارامتری برای ارزیابی مقاومت اشکال مختلف در برابر پیچش مورد استفاده قرار می‌گیرد. ممان اینرسی قطبی نیم دایره از فرمول زیر به دست می‌آید:

$$
J _ z = \left ( \frac { \pi }{ ۴ } - \frac { ۸ }{ ۹ \pi } \right ) r ^ ۴
$$

• J_z: گشتاور قطبی مقطع نیم دایره حول محور مرکزی z (محور عمود بر مرکز هندسی مقطع)
• r: شعاع نیم‌دایره

قضیه محورهای موازی در ممان اینرسی سطح نیم دایره

در بخش‌های قبلی، روابط موجود برای محاسبه ممان اینرسی نیم دایره را ارائه کردیم. در تمام فرمول‌های ارائه شده، محور مبنای محاسبات، محور گذرنده از مرکز هندسی مقطع بود.

در این بخش، قصد داریم ممان اینرسی نیم دایره حول محور مبنای موازی با محورهای مرکزی را توضیح دهیم. به این منظور، تصویر زیر را در نظر بگیرید.

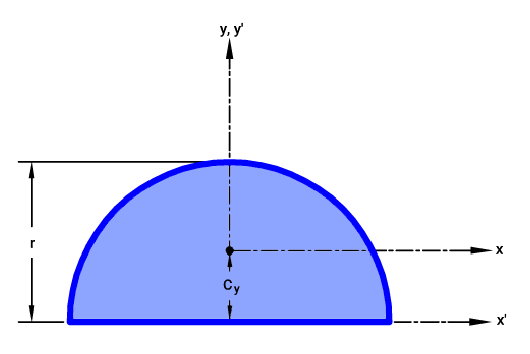
پارامترهای نمایش داده شده در تصویر بالا عبارت هستند از:

• x: محور افقی گذرنده از مرکز هندسی نیم‌دایره
• y: محور عمودی گذرنده از مرکز هندسی نیم‌دایره
• 'x: محور موازی با x و گذرنده از قطر نیم‌دایره
• 'y: محور موازی با y (در اینجا، این محور بر روی y منطبق است.)
• r: شعاع نیم‌دایره
• C_y: فاصله مرکز میانه قطر نیم‌دایره تا مرکز هندسی آن

در مبحث گشتاور دوم سطح، رابطه‌ای بین ممان اینرسی نسبت به محور مرکزی x و محورهای موازی با آن (نظیر محور 'x در شکل بالا) وجود دارد که با عنوان قضیه محورهای موازی شناخته می‌شود. این رابطه عبارت است از:

$$
I ' = I + A d ^ ۲
$$

• 'I: ممان اینرسی سطح نسبت به محور موازی با محور مرکزی
• I: ممان اینرسی سطح نسبت به محور مرکزی
• A: مساحت شکل
• d: فاصله بین محور موازی مورد نظر با محور مرکزی

به عنوان مثال، اگر بخواهیم ممان اینرسی نیم‌دایره را حول محور 'x (محور موازی با محور مرکزی x) به دست بیاوریم، خواهیم داشت:

$$
I _ { x ^ { ' } } = I _ x + A d ^ ۲
$$

$$
I _ { x ^ { ' } } = \left ( \frac { \pi }{ ۸ } - \frac { ۸ }{ ۹ \pi } \right ) r ^ ۴ + \left ( \frac { ۱ }{ ۲ } \pi r ^ ۲ C _ y ^ ۲ \right )
$$

C_y، فاصله مرکز هندسی نیم‌دایره تا محور 'x است که از رابطه زیر به دست می‌آید:

$$ C _ y = \frac { ۴ r }{ ۳ \pi } $$

به این ترتیب، داریم:

$$
I _ { x ^ { ' } } = \left ( \frac { \pi }{ ۸ } - \frac { ۸ }{ ۹ \pi } \right ) r ^ ۴ + \left ( \frac { ۱ }{ ۲ } \pi r ^ ۲ (\frac { ۴ r }{ ۳ \pi }) ^ ۲ \right )
$$

$$
I _ { x ^ { ' } } = \left ( \frac { \pi }{ ۸ } - \frac { ۸ }{ ۹ \pi } \right ) r ^ ۴ + \left ( \frac { ۱ }{ ۲ } \pi r ^ ۲ \frac { ۱۶ r ^ ۲ }{ ۹ \pi ^ ۲ } \right )
$$

$$
I _ { x ^ { ' } } = \left ( \frac { \pi }{ ۸ } - \frac { ۸ }{ ۹ \pi } \right ) r ^ ۴ + \left ( \frac { ۸ r ^ ۴ }{ ۹ \pi } \right )
$$

$$
I _ { x ^ { ' } } = \frac { \pi }{ ۸ } r ^ ۴ - \frac { ۸ r ^ ۴ }{ ۹ \pi } + \frac { ۸ r ^ ۴ }{ ۹ \pi }
$$

$$
I _ { x ^ { ' } } = \frac { \pi }{ ۸ } r ^ ۴
$$

به این ترتیب، اگر محور مبنای محاسبه ممان اینرسی سطح نیم‌دایره از روی قطر آن عبور کند (محور مبنا، موازی با محور مرکزی x باشد)، مقدار گشتاور دوم سطح حول آن از رابطه بالا به دست می‌آید. محور 'y، بر روی محور y‌ منطبق است. بنابراین، ممان اینرسی سطح نیم‌دایره حول این محور، همان ممان اینرسی نیم‌دایره حول محور y‌ خواهد بود:

$$
I _ { y ^ { ' } } = I _ y = \frac { \pi r ^ ۴}{ ۸ }
$$

در اکثر منابع، فرمول بالا را به عنوان ممان اینرسی نیم دایره معرفی می‌کنند.

مثال ۲: محاسبه ممان اینرسی نیم دایره حول محور دلخواه

اگر قطر نیم‌دایره زیر برابر با ۴ سانتی‌متر باشد، ممان اینرسی سطح آن حول محور 'y‌ (محور مماس بر دایره و موازی با محور مرکزی y) چقدر است؟

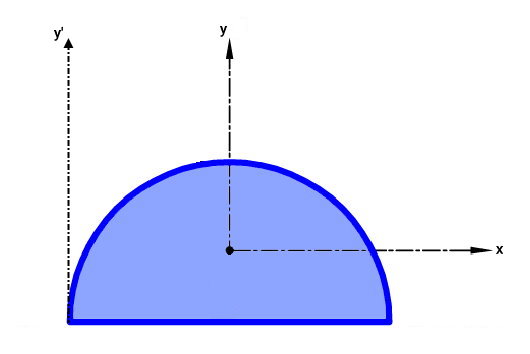
اگر محور 'y، مماس بر کمان نیم‌دایره باشد، فاصله آن تا محور مرکزی y برابر با شعاع نیم‌دایره خواهد بود. به دلیل موازی بودن این محور با y، ممان اینرسی نیم‌دایره حول آن از رابطه زیر به دست می‌آید:

$$
I ' = I + A d ^ ۲
$$

• 'I: ممان اینرسی سطح نسبت به محور موازی با محور مرکزی
• I: ممان اینرسی سطح نسبت به محور مرکزی
• A: مساحت شکل
• d: فاصله بین محور موازی مورد نظر با محور مرکزی برابر با شعاع نیم‌دایره

اکنون، هر یک از پارامترهای بالا را مورد بررسی قرار می‌دهیم. ممان اینرسی سطح نیم‌دایره نسبت به محور مرکزی y عبارت است از:

$$ I _ y = \frac { \pi r ^ ۴}{ ۸ } $$

مساحت نیم‌دایره با نصف مساحت دایره برابری می‌کند. به این ترتیب، داریم:

$$ A = \frac {۱} {۲} \times \pi r^۲ $$

در فرمول‌های بالا، r، شعاع نیم‌دایره را نمایش می‌دهد. این پارامتر، نصف قطر نیم‌دایره است:

$$
r = \frac { d }{ ۲ }
$$

$$
r = \frac { ۴ }{ ۲ }
$$

$$ r = ۲ $$

d، فاصله بین محور 'y و y است. این فاصله، با اندازه شعاع نیم‌دایره (۲ سانتی‌متر) برابری می‌کند. با دانستن این موارد، رابطه زیر را حل می‌کنیم:

$$
I _ { y ^ { ' } } = I _ y + A d ^ ۲
$$

$$
I _ { y ^ { ' } } = \frac { \pi r ^ ۴}{ ۸ } + \frac { \pi r^۲ } {۲} d ^ ۲
$$

$$
I _ { y ^ { ' } } = \frac { \pi ۲ ^ ۴}{ ۸ } + \frac { \pi ۲ ^ ۲ \times ۲ ^ ۲ } {۲}
$$

$$
I _ { y ^ { ' } } = \frac { ۱۶ \pi }{ ۸ } + \frac { ۱۶ \pi } {۲}
$$

$$
I _ { y ^ { ' } } = ۲ \pi + ۸ \pi
$$

$$
I _ { y ^ { ' } } = ۱۰ \pi
$$

اگر عدد پی را برابر با ۳/۱۴ در نظر بگیریم، ممان اینرسی نیم‌دایره حول محور 'y برابر با ۳۴/۱ سانتی‌متر به توان چهار (۳/۱۴cm^۴) می‌شود.

اثبات ممان اینرسی نیم دایره

به منظور اثبات ممان اینرسی نیم دایره نسبت به محور مرکزی x، ابتدا باید فرمول ممان اینرسی نیم دایره نسبت به محور گذرنده از قطر آن را به دست بیاوریم.

شکل زیر، المان dA و پارامترهای مرتبط با آن را برای یک دایره و بر روی دستگاه مختصات قطبی نمایش می‌دهد.

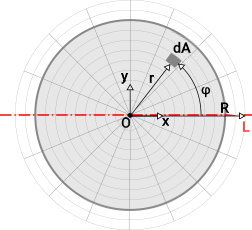
فرمول کلی ممان اینرسی حول محور مرکزی x را در نظر بگیرید:

$$
I _ x = \int \int _ { A } { y ^ ۲ dA }
$$

dA، یک المان دیفرانسیلی از سطح نیم‌دایره است. در شکل‌های دایره‌ای، این المان از رابطه زیر به دست می‌آید:

$$ d A = d r d s = d r ( r d \phi ) = r d r d \phi $$

• dA: مساحت دیفرانسیلی دایره
• dr: فاصله دیفرانسیلی هر جز تا مرکز مختصات
• ds: طول دیفرانسیلی کمان حاصل از زاویه تفاضلی
• r: فاصله هر جز تا مرکز مختصات
• dφ: زاویه دیفرانسیلی بین محور قطبی و هر جز

برای یک دایره کامل، dA در بازه‌های زیر قرار می‌گیرد:

$$
r \in [ ۰ , R ]
$$

$$
\phi \in [ ۰ , ۲ \pi ]
$$

در نیم‌دایره، بازه قرارگیری dA متفاوت است. برای درک این تفاوت، یک نیم‌دایره را بر روی دستگاه مختصات قطبی در نظر بگیرید.

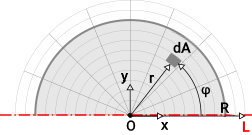
همان‌طور که مشاهده می‌کنید، در یک نیم‌دایره، المان dA در محدوده زاویه ۰ تا ۱۸۰ درجه قرار دارد. بنابراین:

$$
r \in [ ۰ , R ]
$$

$$
\phi \in [ ۰ , ۲ \pi ]
$$

اکنون، نقطه‌ای مانند P را از سطح نیم‌دایره انتخاب می‌کنیم. این نقطه، در فاصله r از محل تقاطع محورهای مبنا (نقطه O) قرار دارد و با محور قطبی، زاویه Φ می‌سازد.

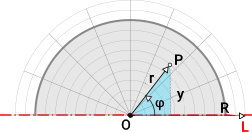
اگر نقطه P را به O وصل کرده و از آن به محور L عمود کنیم، یک مثلث قائم‌الزاویه مانند شکل بالا به وجود می‌آید. بر اساس نسبت‌های مثلثاتی داریم:

$$
\sin \phi = \frac { y }{ r }
$$

$$
y = r \sin \phi
$$

بار دیگر فرمول کلی ممان اینرسی سطح را می‌نویسیم:

$$
I _ x = \int \int _ { A } { y ^ ۲ dA }
$$

اکنون، به جای dA و y، روابطی که به دست آوردیم را جایگزین می‌کنیم:

$$
I _ x = \int \int _ { A } { ( r \sin \phi ) ^ ۲ r \space d r d \phi }
$$

بازه انتگرال‌گیری dr برابر با ۰ تا R و بازه انتگرال‌گیری dΦ برابر با ۰ تا π (زاویه ۰ تا ۱۸۰ درجه) است:

$$
I _ x = \int _ {۰} ^ {R} \int _ { ۰ } ^ { \pi } { ( r \sin \phi ) ^ ۲ r \space d r d \phi }
$$

$$
I _ x = \int _ {۰} ^ {R} \int _ { ۰ } ^ { \pi } { r ^ ۳ \sin ^ ۲ \phi \space d r d \phi }
$$

برای انتگرال‌گیری بر مبنای dΦ، متغیر r، یک ثابت در نظر گرفته می‌شود. بنابراین می‌توانیم آن را به پشت انتگرال اول انتقال دهیم:

$$
I _ x = \int _ { ۰ } ^ { R } \left( r ^ ۳ \int _ { ۰ } ^ { \pi } \sin ^ ۲ \phi \space d \phi \right ) d r
$$

برای انتگرال داخلی داریم:

$$
\sin ^ ۲ \phi = \frac { ۱ - \cos { ۲ \phi }}{ ۲ }
$$

$$
\int _ { ۰ } ^ { \pi } \sin ^ ۲ \phi \space d \phi = \int _ { ۰ } ^ { \pi } \frac { ۱ - \cos { ۲ \phi }}{ ۲ } \space d \phi
$$

$$
\int _ { ۰ } ^ { \pi } \frac { ۱ - \cos { ۲ \phi }}{ ۲ } \space d \phi = \int _ { ۰ } ^ { \pi } \left( \frac { ۱ }{ ۲ } -\frac { \cos { ۲ \phi } }{۲} \space \right) d \phi
$$

$$
\left[ \frac { ۱ }{ ۲ } \phi \right] _ { ۰ } ^ { \pi } - \left[ \frac { ۱ }{ ۴ } \sin { \phi } \right] _ { ۰ } ^ { \pi }
$$

$$
\left( \frac { \pi }{ ۲ } - ۰ \right) - \left( \frac { ۱ }{ ۴ } \sin { ۲ \phi } - \frac { ۱ }{ ۴ } \sin { ۰ } \right)
$$

$$ \frac { \pi }{ ۲ } - ( ۰ - ۰ ) = \frac { \pi }{ ۲ } $$

جواب انتگرال اول در بازه ۰ تا π برابر با $$ \frac { \pi }{ ۲ } $$ شد. به این ترتیب، برای انتگرال دوم داریم:

$$
I _ x = \int _ { ۰ } ^ { R } \left( r ^ ۳ \frac { \pi }{ ۲ } \right ) d r
$$

$$ \frac { \pi }{ ۲ } $$ عدد ثابت است و به پشت انتگرال انتقال داده می‌شود:

$$
I _ x = \frac { \pi }{ ۲ } \int _ { ۰ } ^ { R } r ^ ۳ d r
$$

$$
I _ x = \frac { \pi }{ ۲ } \left[ \frac { r ^ ۴ }{ ۴ } \right ] _ { ۰ } ^ { R }
$$

$$
I _ x = \frac { \pi }{ ۲ } \left ( \frac { R ^ ۴ }{ ۴ } - ۰ \right )
$$

$$
I _ x = \frac { \pi R ^ ۴ }{ ۸ }
$$

در نتیجه، فرمول ممان اینرسی نیم دایره حول محور گذرنده از قطر آن اثبات می‌شود. اگر این فرمول را درون قضیه محورهای موازی قرار دهیم، به فرمول ممان اینرسی نیم دایره حول محور افقی گذرنده از مرکز هندسی مقطع می‌رسیم. در صورت نوشتن رابطه کلی ممان اینرسی حول محور y، می‌توانیم فرمول گشتاور دوم سطح نیم دایره حول این محور را نیز اثبات کنیم. در این حالت، بازه انتگرال‌گیری برحسب dΦ از $$ - \frac { \pi } { ۲ } $$ تا $$ \frac { \pi } { ۲ } $$ خواهد بود.

ممان اینرسی شکل های مرتبط با نیم دایره

نیم‌دایره، یکی از قطاع‌های شناخته شده دایره است. به بخشی از دایره که از یک کمان و دو شعاع تشکیل شود، قطاع می‌گویند. در این بخش، به معرفی فرمول های ممان اینرسی دایره و قطاع‌های آن می‌پردازیم.

ممان اینرسی دایره

دایره، یک شکل متقارن (دارای تقارن محوری و تقارن مرکزی) است. این شکل، از ممان اینرسی بهتری نسبت به دیگر مقطع‌های دوبعدی بهره می‌برد. تصویر زیر، یک مقطع دایره‌ای به شعاع R را در دستگاه مختصات دوبعدی x-y نمایش می‌دهد.

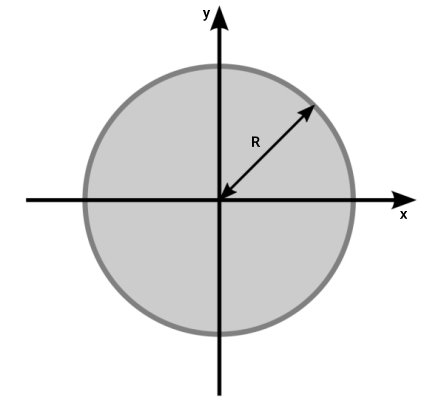
محورهای x و y، از مرکز هندسی دایره عبور می‌کنند. اگر بخواهیم ممان اینرسی سطح دایره نسبت به این محورها به دست بیاوریم، از فرمول‌های زیر استفاده می‌کنیم:

$$
I _ x = \frac { \pi }{ ۴ } R ^ ۴
$$

$$
I _ y = \frac { \pi }{ ۴ } R ^ ۴
$$

• I_x: گشتاور دوم سطح دایره‌ای نسبت به محور مرکزی x
• I_y: گشتاور دوم سطح دایره‌ای نسبت به محور مرکزی y
• R: شعاع سطح مقطع دایره‌ای

ممان اینرسی قطبی سطح دایره، از جمع ممان‌های بالا به دست می‌آید:

$$
J = I _ z = I _ x + I _ y =\frac { \pi }{ ۴ } R ^ ۴ + \frac { \pi }{ ۴ } R ^ ۴
$$

$$
J = I _ z = \frac { \pi } { ۲ } R ^ ۴
$$

• J: ممان اینرسی قطبی
• I_z: گشتاور دوم سطح نسبت به محور مرکزی z
• R: شعاع دایره

در صورت برابر بودن شعاع‌ها، نسبت ممان اینرسی سطح دایره به ممان اینرسی سطح نیم‌دایره برابر با ۲ است.

ممان اینرسی ربع دایره

ربع دایره، یکی دیگر از قطاع‌های شناخته شده دایره است. این قطاع، از تقسیم دایره به چهار قسمت مساوی به وجود می‌آید. تصویر زیر، مقطع یک ربع دایره در دستگاه مختصات دوبعدی x-y را نمایش می‌دهد.

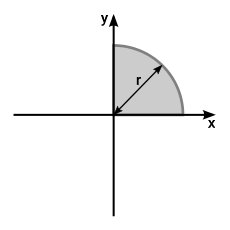
ممان اینرسی سطح ربع دایره بالا حول محورهای x و y عبارت است از:

$$
I _ x = \frac { \pi r ^ ۴ }{ ۱۶ }
$$

$$
I _ y = \frac { \pi r ^ ۴ }{ ۱۶ }
$$

• I_x: گشتاور دوم سطح ربع دایره نسبت به محور x
• I_y: گشتاور دوم سطح ربع دایره نسبت به محور y
• r: شعاع سطح مقطع ربع‌دایره

در این حالت، ممان اینرسی ربع‌دایره، یک‌چهارم ممان اینرسی دایره کامل (با شعاع برابر) می‌شود. توجه داشته باشید که x و y، از مرکز هندسی ربع‌دایره عبور نمی‌کنند یا به عبارت دیگر، مرکزی نیستند. در تصویر زیر، محورهای x و y، محورهای مرکزی در نظر گرفته می‌شوند.

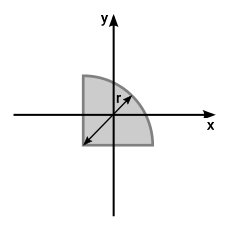
در این حالت، ممان اینرسی ربع دایره حول محورهای مرکزی x و y‌ از روابط زیر به دست می‌آید:

$$
I _ x = \left ( \frac { \pi }{ ۱۶ } - \frac { ۴ }{ ۹ \pi } \right ) r ^ ۴ = \approx ۰/۰۵۴۹ r ^ ۴
$$

$$
I _ y = \left ( \frac { \pi }{ ۱۶ } - \frac { ۴ }{ ۹ \pi } \right ) r ^ ۴ = \approx ۰/۰۵۴۹ r ^ ۴
$$

• I_x: گشتاور دوم سطح ربع دایره نسبت به محور مرکزی x
• I_y: گشتاور دوم سطح ربع دایره نسبت به محور مرکزی y
• r: شعاع سطح مقطع ربع‌دایره

ممان اینرسی قطاع دایره

تصویر زیر، ممان اینرسی قطبی از دایره را نمایش می‌دهد که محل تقاطع شعاع‌های آن، بر روی محورهای x و y‌ قرار دارد.

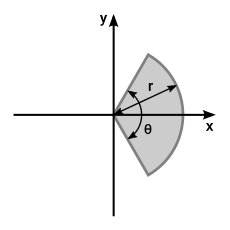
ممان اینرسی این قطع حول محور x، با استفاده از فرمول زیر محاسبه می‌شود:

$$
I = ( \theta - \sin \theta ) \frac { r ^ ۴ }{ ۸ }
$$

• I: گشتاور دوم سطح قطاع دایره نسبت به محور x (محور نیم‌ساز زاویه مقابل به کمان قطاع)
• r: شعاع قطاع
• θ: زاویه مقابل به کمان

به عنوان مثال، اگر در رابطه بالا، زاویه θ را برابر با π (زاویه ۱۸۰ درجه و معرف نیم‌دایره) در نظر بگیریم، رابطه ممان اینرسی مقطع نیم‌دایره به دست می‌آید.

سوالات متداول در رابطه با ممان اینرسی نیم دایره

در این بخش، به برخی از پرتکرارترین سوالات مرتبط با ممان اینرسی نیم دایره به طور خلاصه پاسخ می‌دهیم.

تعریف ممان اینرسی سطح نیم دایره چیست ؟

ممان اینرسی مقطع نیم دایره، کمیتی است که پراکندگی نقاط سطح نیم‌دایره را نسبت به یک محور مشخص نمایش می‌دهد.

فرمول ممان اینرسی مقطع نیم دایره چیست ؟

فرمول ممان اینرسی سطح نیم دایره، I=πr^۴/۸ است.

فرمول ممان اینرسی مقطع دایره چیست ؟

فرمول ممان اینرسی سطح دایره، I=πr^۴/۴ است.

رابطه بین ممان اینرسی دایره و نیم دایره چیست ؟

اگر سطح یک دایره را از روی محور مبنا نصف کنیم، ممان اینرسی آن حول همان محور نصف می‌شود.

فرمول ممان اینرسی مقطع ربع دایره چیست ؟

فرمول ممان اینرسی نیم‌دایره حول محور مرکزی x و y برابر با ۰/۰۵۴۹r^۴ است.

قضیه محورهای موازی در محاسبه ممان اینرسی مقطع نیم دایره ای چیست ؟

قضیه محورهای موازی، رابطه ممان اینرسی نیم دایره حول محورهای مبنا و محورهای موازی با آن‌ها است. بر اساس این رابطه، اگر ممان اینرسی نیم دایره حول یک محور مشخص را داشته باشیم، می‌توانیم ممان اینرسی سطح حول محورهای موازی با محور مبنای اولیه را به دست بیاوریم. برای این کار، به فاصله بین دو محور موازی و مساحت مقطع نیز نیاز خواهیم داشت.