معادله خط و ترسیم آن – به زبان ساده

در بیشتر موارد نیاز داریم که یک تابع خطی را ترسیم کنیم یا معادله خط را روی مختصات دکارتی نمایش دهیم. در چنین مواردی باید از اصول و شیوه‌های بیان یک خط در مختصات دکارتی آگاه باشیم و بتوانیم با استفاده از تکنیک‌ نقطه‌یابی آن‌ها را رسم کنیم. در این نوشتار از مجله فرادرس به بررسی شیوه‌های مختلف نمایش خط و همچنین چگونگی رسم کردن خطوط براساس هر یک از این شیوه‌ها می‌پردازیم.

برای آگاهی بیشتر در مورد تعریف خط و مختصات دکارتی بهتر است ابتدا مطلب معادله خط — به زبان ساده را مطالعه کرده باشید. همچنین مطالعه متن مربوط به مشتق که در بلاگ فرادرس با عنوان مشتق — به زبان ساده از مجله فرادرس خالی از لطف نیست.

معادله خط و ترسیم آن

همانطور که می‌دانید، خط یک مفهوم انتزاعی است که دارای فقط یک بعد است. در هندسه اقلیدسی، کوتاه‌ترین فاصله بین دو نقطه را یک خط راست می‌گویند.

معمولا به چند شیوه مختلف معادله خط را بیان می‌کنند. در ادامه به این روش‌ها آشنا می‌شویم.

• نمایش براساس دو نقطه: با توجه به تعریف خط، می‌دانیم که یک خط راست کوتاه‌ترین فاصله بین دو نقطه است. بنابراین معادله چنین خطی را برحسب مختصات دو نقطه‌اش از خط می‌توان به صورت $$y-y_1=\big(\frac{y_1-y_2}{x_1-x_2}\big)(x-x_1)$$ نشان داد که $$(x_1,y_1)$$ مختصات نقطه اول و $$(x_2,y_2)$$ مختصات نقطه دوم است.
• نمایش براساس شیب و یک نقطه: اگر برای نمایش معادله خط، فقط از یک نقطه و شیب خط استفاده شود، فرم کلی آن را می‌توان به صورت $$y-y_0=m(x-x_0)$$ نمایش داد. در این حالت m شیب خط و $$(x_0,y_0)$$ نقطه‌ای از خط است که مختصات آن مشخص است.
• نمایش براساس شیب و عرض از مبدا: شکل کلی برای معادله خط در این حالت به صورت y=mx+b است که در آن m شیب خط و b عرض از مبدا است. اگر x=0 باشد، b مقداری را روی محور عمودی نشان می‌دهد که خط مورد نظر محور عمودی را قطع می‌کند.
• نمایش ضمنی معادله خط: در این حالت فرم نمایش به صورت ax+by+c=0 است و a,b,c را پارامترهای خط می‌گویند. هر چند این رابطه به صورت یک معادله (طرف راست برابر با صفر) نوشته شده ولی می‌توان آن را به صورت‌هایی دیگری که در بالا گفته شد، در آورد.

هرچند بیان معادله خط به شیوه‌های مختلفی امکان‌پذیر است، ولی همیشه می‌توان از یک روش استفاده کرد و پارامترهای معادله خط در روش دیگر را بدست آورد. هر یک از این شیوه‌های مختلف بیان معادله خط، در جاهایی کاربرد دارد. در ادامه براساس مثال‌هایی به بررسی این شیوه‌ها می‌پردازیم.

مثال ۱

معادله خطی را بیابید که از دو نقطه با مختصات $$A(2,3)$$ و $$B(6,4)$$ می‌گذرد. با توجه به مشخص بودن دو نقطه از خط روش نوشتن معادله خط تعیین شده و می‌نویسیم:

$$x_1=2, y_1=3,\;\;\;\;x_2=6,y_2=4$$

 $$\large y-y_1=\big(\frac{y_1-y_2}{x_1-x_2}\big)(x-x_1)\rightarrow y-3=\big(\frac{3-4}{2-6}\big)(x-2)$$

$$\large y-3=\frac{-1}{-4}(x-2)\rightarrow y=\frac{1}{4}(x-2)+3\rightarrow y=\frac{1}{4}x-\frac{1}{2}+3=\frac{1}{4}x+\frac{5}{2}$$

از طرفی برای ترسیم خطی با معادله $$y=\frac{1}{4}x+\frac{5}{2}$$ کافی است با نقطه یابی، دو نقطه از مختصات دکارتی را بیابید که در معادله خط صدق کنند. سپس با مشخص کردن این نقاط در صفحه مختصات، آن‌ها را به هم وصل کنید و از دو طرف ادامه دهید. به این ترتیب معادله خط مورد نظر رسم شده است. هر چند دو نقطه اصلی A و B برای این خط موجود است، ولی برای تاکید بیشتر این نقاط را براساس معادله خط پیدا و ترسیم می‌کنیم. معمولا راحت‌ترین حالت مقدار دهی به x و محاسبه y از طریق معادله خط است. پس فرض کنید که x=2 باشد، به این ترتیب مقدار $$y=\frac{1}{4}(2)+\frac{5}{2}=3$$ عرض نقطه اول را نشان می‌دهد. پس مختصات نقطه اول به صورت $$(2,3)$$ خواهد بود. برای نقطه دوم مقدار طول نقطه را x=6 انتخاب می‌کنیم. در نتیجه مقدار عرض نقطه برابر با $$y=\frac{1}{4}(6)+\frac{5}{2}=4$$ خواهد بود. این مراحل را می‌توان طبق جدول زیر نشان داد.

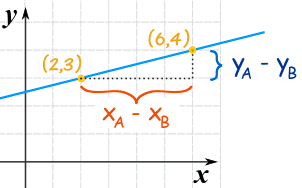
در این حالت ضریب x یعنی مقدار $$\frac{1}{4}$$ شیب خط نامیده می‌شود و مقدار ثابت یعنی $$\frac{5}{2}$$ نیز عرض از مبدا خواهد بود.

فیلم محاسبه شیب خط و عرض از مبدا در ریاضی + مثال‌های مختلف (آموزش رایگان) در فرادرس

کلیک کنید

مثال ۲

معادله خطی را رسم کنید که شیب آن برابر با ۳ و از نقطه‌ای به مختصات $$(3,2)$$ بگذرد. طبق این روش باید مختصات نقطه را به صورت $$x_0,y_0$$ در نظر بگیریم و محاسبات را انجام دهیم. بنابراین خواهیم داشت:

$$\large x_0=3, \;y_0=2$$

$$\large y-y_0=m(x-x_0)\rightarrow y-2=3(x-3)\rightarrow y=3x-9+2\rightarrow y=3x-7$$

برای ترسیم چنین خطی در مختصات دکارتی، باز هم از جدولی مانند جدول بالا، کمک می‌گیریم.

همانطور که می‌بینید نقطه اول همان مختصاتی را دارد که در مسئله گفته شد ولی نقطه دوم از طریق نقطه‌یابی بدست آمده است. بنابراین شکل این خط با اتصال این نقاط به صورت زیر خواهد بود.

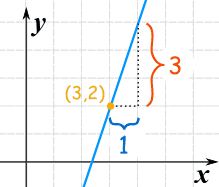
نکته: در اینجا شیب خط، نشان دهنده تانژانت زاویه‌ای است که این خط با محور افقی خواهد ساخت. این مقدار را می‌توان از طریق مشتق‌گیری از معادله خط نیز بدست آورد. از آنجایی که در اینجا شیب خط برابر با ۳ محاسبه شده است، زاویه مورد نظر باید حدود 71.5 درجه باشد.

مثال ۳

معادله خطی را رسم کنید که شیب آن برابر با ۳ و عرض از مبدا آن نیز برابر با ۷- باشد. مشخص است که معادله خط در این حالت به صورت زیر نوشته می‌شود.

$$\large y=3x-7$$

طبق روش ترسیمی احتیاج به دو نقطه داریم که طبق جدول زیر بدست می‌آید.

همانطور که می‌بینید، نقاط حاصل از این معادله خط با مثال قبلی مطابقت دارد. در نتیجه خط ترسیم شده درست به مانند آن مثال خواهد بود.

مثال ۴

معادله خط مربوط به مثال ۳ را به صورت استاندارد نشان دهید.

همانطور که مشخص است باید ضرایب متغیرهای x و y را بدست آورده و معادله را به صورتی بنوسیم که در یک طرف تساوی صفر قرار گرفته باشد. بنابراین خواهیم داشت:

$$\large y=3x-7\rightarrow y-3x+7=0$$

بنابراین مقدار $$a=-3,b =1 , c=7$$ خواهد بود. برای ترسیم این خط نیز درست به مانند روش‌ نقطه یابی با استفاده از دو نقطه، خط را ترسیم می‌کنیم.

مثال ۵

معادله خطی را بدست آورید که از نقطه A و B به مختصات $$(2,1)$$ و $$(2,4)$$ بگذرد. این خط را ترسیم کنید.

از آنجایی که دو نقطه در اختیارمان است باید از طریق محاسبات معادله خط براساس دو نقطه عمل کنیم. ولی مشکلی در این میان وجود دارد:

$$x_1=2, y_1=1,\;\;\;\;x_2=2,y_2=4$$

 $$\large y-y_1=\big(\frac{y_1-y_2}{x_1-x_2}\big)(x-x_1)\rightarrow y-1=\big(\frac{1-4}{2-2}\big)(x-2)$$

همانطور که می‌بینید، مخرج کسر برابر با صفر است. بنابراین در این حالت شیب خط بی‌نهایت شده و در نتیجه خط با محور افقی زاویه ۹۰ درجه می‌سازد. از طرفی این خط باید از دو نقطه با طولی برابر با ۲ بگذرد. پس کافی است خطی موازی محور عمودی رسم کنیم که محور افقی را در نقطه x=2 قطع کند. چنین خطی را با معادله x=2 نشان می‌دهیم.