قضیه اساسی جبر – به زبان ساده
قضیه اساسی جبر، آنطور که به نظر میرسد، اولین قضیه یا ابتدا راه جبر و مقابله نیست، بلکه قضیهای جذاب در مورد «چند جملهایها» (Polynomial) است. این قضیه بیان میکند که تعداد ریشههای ممکن برای یک چند جملهای از درجه آن تبعیت میکند. به این ترتیب میتوان تعداد ریشههای چند جملهای را حدس زد و سپس به دنبال جستجو کرد. البته باید توجه داشت که ممکن است این ریشهها حقیقی مقدار نباشند. در نتیجه در ادامه در مورد اعداد مختلط و ریشههای مختلط معادلات حاصل از چند جملهایها صحبت خواهیم کرد.
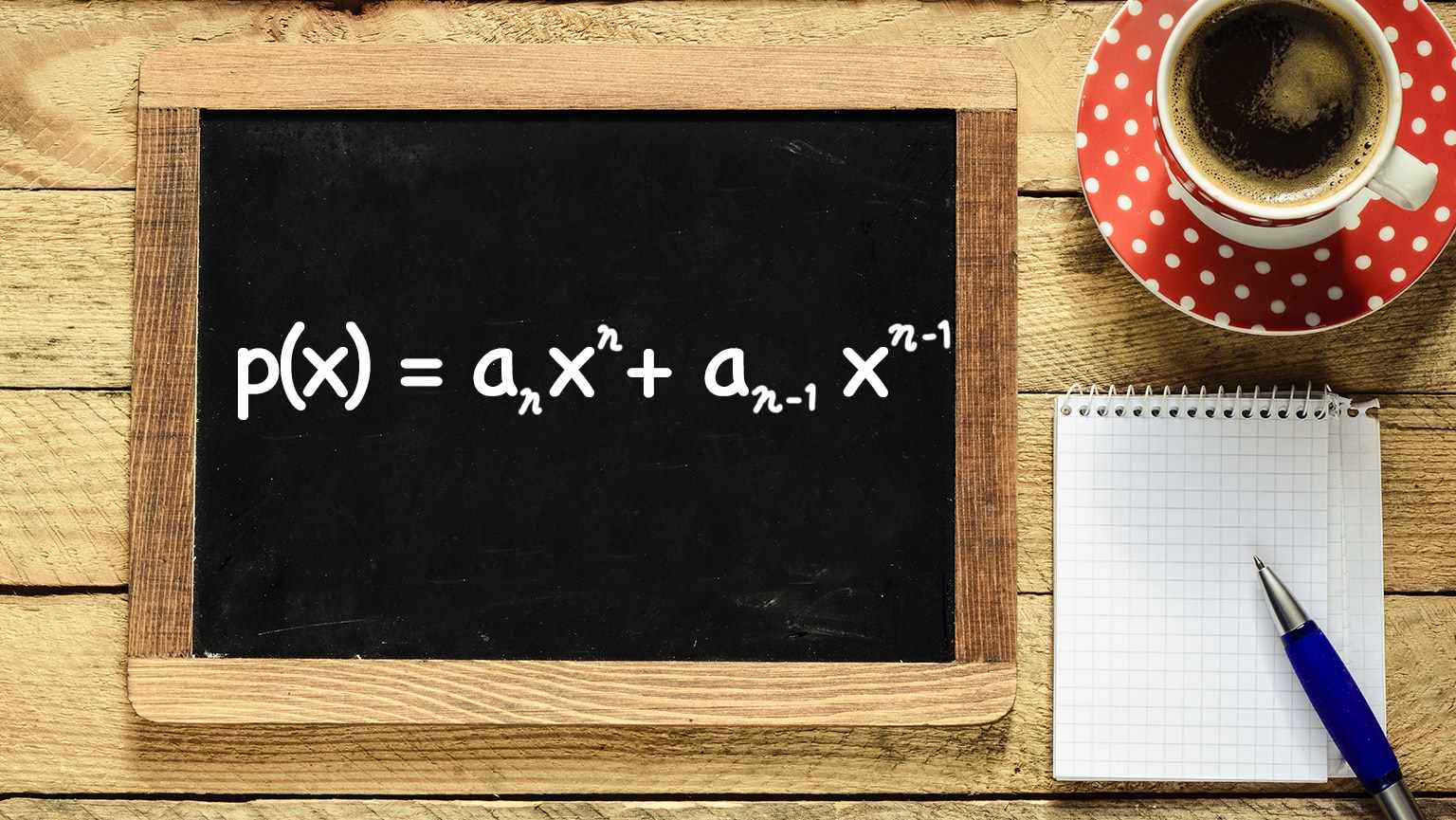
هر چند مباحث این نوشتار ساده هستند ولی برای درک بهتر آن، مطالعه مطلب چندجملهایها – به زبان ساده و همچنین معادله درجه دو — به زبان ساده توصیه میشود. البته مطالعه مطلب معادلات و نامعادلات ریاضی — پیدایش و کاربردها نیز خالی از لطف نیست.
قضیه اساسی جبر
اگر صورت کلی یک چند جملهای درجه n را در نظر بگیرید، قضیه اساسی جبر بیان میکند که تعداد ریشههای آن برابر با n است. این قضیه به صورت زیر است:
یک چند جملهای درجه n دارای n ریشه است.
نکته: توجه کنید که در اینجا همه ریشههای چند جملهای (حقیقی و مختلط) در نظر گرفته شده است. در هر صورت اگر منظور ریشههای حقیقی باشد میتوان گفت که تعداد ریشههای حقیقی حداکثر برابر با n خواهد بود.
شکل کلی یک چند جملهای درجه n به صورت زیر نوشته میشود که در آن ضرایب چند جملهای و x نیز متغیر آن است.
همانطور که دیده میشود، بزرگترین توان x نیز در اینجا، برابر با n در نظر گرفته شده است.
نکته: در این عبارت، توانهای x از صفر شروع و تا n ادامه پیدا کردهاند. بنابراین یک چند جملهای کامل یا استاندارد، دارای n+1 جمله است.
مثلا فرم استاندارد و کلی چند جملهای درجه ۳ به صورت زیر است:
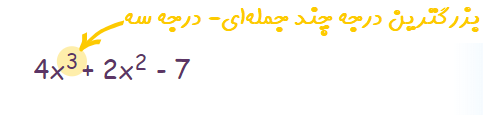
ممکن است در یک چندجملهای درجه n، همه جملات به کار نرفته باشند. برای مثال فرض کنید که چند جملهای درجه ۴ به صورت زیر نوشته شده باشد:
این چند جملهای درجه ۴ است زیرا بزرگترین توان متغیر (x) برابر با ۴ است. از طرفی سه جمله بیشتر ندارد. در حالیکه صورت کلی چنین جملهای باید ۵ جمله میداشت. ولی به هر حال باز هم آن را یک چند جملهای درجه ۴ مینامیم. چنین چند جملهایهایی را با نام چند جملهای ناقص می شناسیم.
ریشه چند جملهای
منظور از ریشه چند جملهای، مقداری از x است که باعث میشود معادله برقرار شود. فرض کنید به ازای سمت راست برابر با سمت چپ شود. آنگاه را ریشه چند جملهای مینامند.
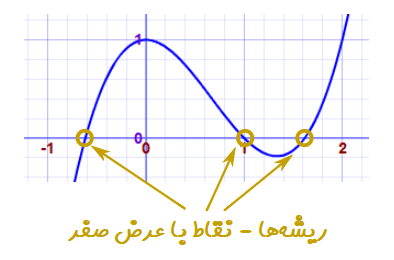
طبق قضیه اساسی جبر، میدانیم که سه ریشه برای چند جملهای درجه ۳ وجود دارد. برای نمایش ریشههای چند جملهای درجه ۳ از منحنی آن کمک میگیریم.در این حالت میتوان ریشههای چند جملهای درجه ۳ را در تصویر زیر مشاهده کرد. همانطور که دیده میشود، منحنی این چند جملهای، در سه نقطه خط y=0 (محور افقی) را قطع کرده است. پس مشخص است که این نقاط ریشه معادله بالا هستند.
مثال
منحنی مربوط به چند جملهای را رسم و ریشههای آن را مشخص کنید.
از آنجایی که درجه این چند جملهای برابر با ۲ است (بزرگترین توان متغیر برابر است با ۲) پس باید دو ریشه داشته باشد. پس چند جملهای را برابر با صفر قرار داده و مینویسیم:
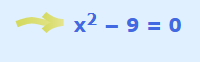
سپس ۹ را از دو طرف کسر میکنیم.

حال از دو طرف ریشه دو گرفته و محاسبات را دنبال میکنیم.
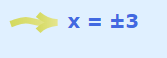
به این ترتیب ۳ و ۳- ریشههای این چند جملهای هستند. از طرفی نمودار این چندجملهای نیز مانند یک سهمی است. محل تقاطع منحنی با محور افقی، ریشهها را نشان میدهد.

بازنویسی چند جملهایها برحسب ریشه
فرض کنید یک چندجملهای درجه ۳ دارید، طبق قضیه اساسی جبر، میدانیم که دارای سه ریشه است.
پس میتوان آن را به صورت زیر بازنویسی کرد.

در اینجا ریشههای چند جملهای است. عبارت نیز فاکتور یا عامل خطی نامیده میشود. برای مثال فرض کنید که چند جملهای مورد نظرمان باشد از آنجایی که میدانیم ریشههای آن برابر با ۳ و ۳- است، فاکتورهای خطی آن برابر با و است. پس میتوان نوشت:
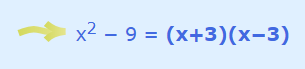
نکته: در این عبارت مقدار a برابر با ۱ است پس از آنجایی که ۱ در ضرب بیاثر است آن را ننوشتهایم.
به این ترتیب آگاهی از ریشههای چندجملهای کمک میکند که آن را به صورت حاصلضرب عاملها بنویسیم. برای آشنایی بیشتر با مفهوم و کاربرد تجزیه به عوامل از یک مثال دیگر کمک میگیریم.
فرض کنید که چند جملهای ما به صورت باشد. درجه این چند جملهای ۲ و تعداد ریشههای آن طبق قضیه اساسی جبر نیز ۲ خواهد بود. برای پیدا کردن ریشههای آن مراحل زیر را طی میکنیم.
ابتدا چندجملهای را برابر با صفر قرار میدهیم.
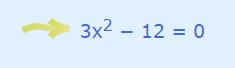
مقسوم علیه مشترک برای ۳ و ۱۲ مقدار ۳ است. پس میتوان از ۳ فاکتور گرفت:

از آنجایی که چند جملهای را به صورت حاصلضرب دو عبارت ۳ و نوشتهایم، که باید برابر با صفر باشند، پس کافی است که فقط معادله را حل کنیم زیرا مقدار ۳ هرگز با ۰ برابر نیست (اگر حاصلضرب دو عبارت برابر با صفر باشد، یا اولی برابر با صفر است یا دومی و یا هر دو).
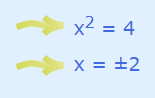
ریشههای معادله درجه ۲ حاصل برابر است با ۲ و ۲-. پس میتوان چند جملهای را به صورت حاصلضرب عاملهایش نوشت. یعنی:
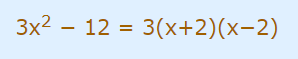
بنابراین آگاهی از ریشههای یک چندجملهای به تجزیه آن به عوامل خطی کمک میکند و برعکس اگر عوامل خطی یک چند جملهای را بدانیم میتوانیم ریشههای آن را پیدا کنیم. از یک مثال دیگر در این زمینه کمک میگیریم.
از شما خواسته شده است که ریشههای چند جملهای درجه دو را پیدا کنید. از آنجایی که این چند جملهای درجه ۲ است میتوان آن را به دو عامل تجزیه کرد.
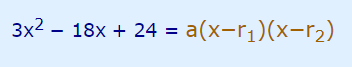
از آنجایی که به نظر میرسد ۳ عامل مشترک برای همه ضرایب است از آن فاکتور میگیریم. سپس با توجه به اتحاد جمله مشترک میتوان عبارت را به صورت سادهتری نوشت.
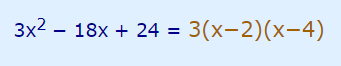
نکته: اتحاد جمله مشترک به صورت نوشته میشود. بنابراین ریشهها برابر با 2 و 4 خواهند بود.
بهتر است این ریشهها را در چندجملهای قرار داده تا صحت عملیات انجام شده را بررسی کنیم. چند جملهای مورد نظر باید در ریشهها، مقداری برابر با صفر داشته باشد.
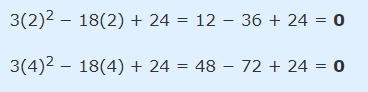
با توجه با محاسبات انجام شده، دیده میشود که ریشههای بدست آمده، صحیح هستند.
اعداد مختلط
گاهی ممکن است ریشه یک چند جملهای، عددی مختلط باشد. پس بهتر است ابتدا با اعداد مختلط آشنا شویم. هر عدد مختلط از دو بخش حقیقی و موهومی تشکیل شده است. در اینجا بخش حقیقی عدد مختلط را با حرف a و بخش موهومی را با b نشان میدهیم. همچنین منظور از i عددی است که مربع آن برابر با ۱- است.
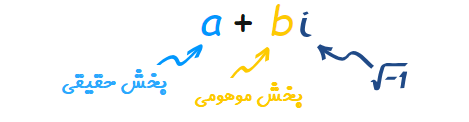
با این توضیحات میخواهیم ریشههای چند جملهای را بدست آوریم. آیا ممکن است این عبارت برابر با صفر باشد. براساس رابطهای که برای ریشههای معادله درجه وجود دارد، معادله را حل میکنیم. در این حالت میتوان نوشت:

مشخص است که هر دو ریشه عدد مختلط هستند. ولی به هر حال قضیه اساسی جبر باز هم نتیجه را پیشبینی کرده بود. با توجه به ریشهها، میتوان چند جملهای را برحسب عوامل به صورت زیر نمایش داد:

زوجهای مزدوج
با توجه به قضیه اساسی جبر، میدانیم چند جملهای درجه n ممکن است دارای ریشههایی باشد که بعضی حقیقی و بعضی نیز مختلط هستند. ولی به هر حال مشخص است که چنین معادلهای دارای n ریشه است. ولی چیزی که در مورد ریشههای مختلط توجه ما را به خود جلب میکند، مزدوج بودن ریشههای مختلط است. میتوان گفت که همیشه ریشههای مختلط مزدوج یکدیگر هستند.
دو عدد مزدوج هستند، اگر حاصلضربشان برابر با باشد.

با توجه به این موضوع مشخص است که تعداد ریشههای مختلط یک چند جملهای باید زوج باشد. به این ترتیب مثلا یک چند جملهای یا ریشه مختلط ندارد، یا دو تا ریشه مختلط، چهار ریشه مختلط یا ... خواهد داشت و هرگز تعداد ریشههای مختلط چندجملهای فرد نخواهد بود.
نکته: البته این حالت فقط زمانی اتفاق میافتد که ضرایب چند جملهای حقیقی باشد. در زمانی که ضرایب چند جملهای مختلط باشند، ممکن است تعداد ریشههای چند جملهای از این قاعده پیروی نکند.
جدول زیر تعداد ریشههای چند جملهای را از لحاظ حقیقی یا مختلط بودن بررسی کرده است:
| درجه چند جمله | تعداد ریشهها | حالات ممکن |
| ۱ | ۱ | ۱ ریشه حقیقی |
| ۲ | ۲ | ۲ ریشه حقیقی یا ۲ ریشه مختلط |
| 3 | 3 | 3 ریشه حقیقی یا ۲ ریشه مختلط و یک ریشه حقیقی |
| 4 | 4 | ۴ ریشه حقیقی- ۲ ریشه مختلط و ۲ ریشه حقیقی - ۴ ریشه مختلط |
| ... | ... | ... |
نکته: با این توضیحات مشخص است که اگر چند جملهای دارای درجه فرد باشد، حتما یک ریشه حقیقی خواهد داشت.
برای مثال اگر معادله را در نظر بگیرید، حتما یک ریشه حقیقی برای آن وجود دارد. مشخص است که این ریشه برابر با ۲ است. نمودار این خط نیز این مسئله را نشان میدهد.
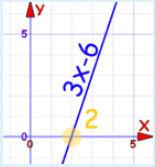
نکته: از نقظه نظر تئوری مجموعهها، مجموعه اعداد مختلط، شامل اعداد حقیقی نیز هست. به این معنی که مجموعه اعداد حقیقی زیرمجموعه اعداد مختلط هستند. اگر مجموعه اعداد حقیقی را با حرف R و مجموعه اعداد مختلط را با C نشان دهیم، داریم:
بنابراین اگر میگویم ریشههای حقیقی منظورمان ریشههایی است که دارای بخش موهومی نیستند.
در یک معادله درجه ۲ اگر ریشهای مختلط وجود نداشته باشد، ریشههای با توجه به نکته بالا، همگی حقیقی خواهند بود. اگر امکان تجزیه یک چند جملهای درجه ۲، به عوامل خطی (بدون استفاده از اعداد مختلط) وجود نداشته باشد، آن را فرم درجه ۲ تجزیه ناپذیر مینامند.
بنابراین هر چند جملهای را میتوان براساس عوامل خطی (Linear Factor) و یا فرم درجه ۲ تجزیه ناپذیر (Irreducible Quadratics) نوشت.
برای مثال چند جملهای درجه ۳ به صورت را میتوان به عوامل زیر تجزیه کرد:
- عامل (فاکتور) خطی
- عامل درجه دوم تجزیه ناپذیر
بنابراین این چند جملهای را میتوان به صورت زیر نوشت:
نکته: از آنجا که عامل دارای ریشه حقیقی نیست، آن را عامل درجه دو تجزیه ناپذیر مینامیم.
روش تشخیص عامل درجه دوم تجزیه ناپذیر
در مطالب فرادرس با عنوان معادله درجه دو — به زبان ساده به توضیح پیدا کردن یشههای حقیقی معادله درجه ۲ به کمک روش دلتا پرداختیم. به این ترتیب مشخص است که وجود ریشههای حقیقی بستگی به علامت دلتا دارد.
اگر فرم معادله درجه ۲ به صورت باشد، آنگاه دلتا () به روش زیر محاسبه میشود.
اگر منفی باشد، معادله درجه ۲ دارای ریشههای مختلط است و در نتیجه تجزیه ناپذیر خواهد بود. برای مثال چند جملهای را در نظر بگیرید. مشخص است که است. بنابراین مقدار دلتا برابر با ۳۱- بدست خواهد آمد.
پس این چند جملهای تجزیه ناپذیر است.
گاهی ممکن است یک عامل دوبار در تجزیه چند جملهای به کار رود. در این حالت میتوان چند جملهای را به صورت حاصلضرب این عوامل تکراری نوشت. برای مثال اگر چند جملهای ما باشد، مشخص است که باید دو ریشه حقیقی داشته باشد.
ولی این دو ریشه با یکدیگر برابرند (زیرا اگر دلتا برابر با ۰ باشد معادله درجه ۲ دارای یک ریشه مضاعف یا دو ریشه برابر خواهد بود).
همچنین اگر چند جملهای را در نظر بگیریم، مشخص است که باید دارای ۴ ریشه باشد. با استفاده از فاکتورگیری و قاعده ضرب داریم:
با توجه به این تجزیه مشخص است که سه ریشه با یکدیگر برابر و مقدارشان برابر با صفر است و یک ریشه هم برابر با ۱- خواهد بود. نمودار زیر که مربوط به این چند جملهای است، بهتر این موضوع را نشان میدهد.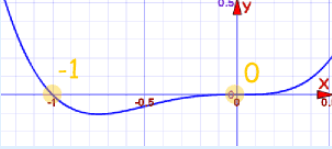
از آنجایی که x در تجزیه چند جملهای ۳ بار تکرار شده است پس ۰ نیز ریشهای است که سه بار تکرار میشود. همچنین با توجه به عامل یا فاکتور که یکبار دیده میشود، یک ریشه برابر با ۱- است. در این حالت ۰ را ریشه تکراری مینامند.
خلاصه و جمعبندی
- معادله حاصل از چند جملهای درجه n دارای n ریشه (حقیقی و مختلط) است.
- چند جملهای درجه n را میتوان به صورت حاصل ضرب عاملهای نوشت.
- ممکن است ریشههای معادله حاصل از یک چند جملهای، مختلط باشند.
- تعداد ریشههای مختلط یک چند جملهای همیشه زوج است.
- یک چند جملهای را میتوان به صورت حاصلضرب عوامل خطی و درجه دوم تجزیه ناپذیر نوشت.
- اگر یک عامل چندین بار در حاصلضرب دیده شود، چند جملهای دارای ریشه مضاعف یا تکراری است.
در صورت علاقهمندی به مباحث مرتبط در زمینهی ریاضیات، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضیات
- مجموعه آموزشهای ریاضی و فیزیک
- مجموعه آموزشهای دبیرستان و پیشدانشگاهی
- چندجملهایها – به زبان ساده
- اتحاد و تجزیه در ریاضی — به زبان ساده
- معادله های پارامتری — به زبان ساده
- معادلات و نامعادلات ریاضی — پیدایش و کاربردها
- معادلات خطی (Linear Equations) — به زبان ساده
- معادله درجه دو — به زبان ساده
- قدر مطلق (Absolute Value) — به زبان ساده
^^













خوب بود مرسی که انگلیسیشم گفتین فقط تو اتحاد جمله مشترک یه x اش جا افتاده به نظرم
x²+(a+b)x+ab
سلام و وقت بخیر؛
فرمول اصطلاح شد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
عالی بود، ممنون که معادل انگلیسی کلمات رو هم در ویدیو عنوان کردید