تابع موبیوس و خصوصیات آن — به زبان ساده

توابع حسابی (Arithmetic Functions) کلید ورود به تئوری یا نظریه اعداد هستند. در نوشتاری دیگر با «تابع اویلر» (Euler Function) و «تابع موبیوس» (Möbius function) را به عنوان توابع حسابی معرفی کردیم. در این مطلب هدف تمرکز روی تابع موبیوس و خصوصیات آن در نظریه اعداد است.

پیشنهاد می‌شود، به منظور آشنایی با نظریه اعداد و مباحث مربوطه، نوشتارهای نظریه اعداد و کاربردهای آن — به زبان ساده و  الگوها و دنباله های متداول عددی – به زبان ساده را بخوانید. همچنین مطالعه قواعد بخش پذیری یا عاد کردن — به زبان ساده و عدد مرکب و خواص آن — به زبان ساده نیز خالی از لطف نیست.

تابع موبیوس و خصوصیات آن

یکی از توابع حسابی مهم در ریاضیات مدرن و نظریه اعداد، «تابع موبیوس» (Möbius function) است که در دسته «توابع ضربی» (Multiplicative Function) قرار می‌گیرد. تابع موبیوس به شکل کلی‌تر در «حساب ترکیبیات» (Combinatorics) نیز دیده می‌شود.

فیلم آموزش ترکیبیات و کاربردها – جامع و کاربردی در فرادرس

کلیک کنید

این تابع توسط دانشمند و ریاضی‌دان آلمانی «آگوست فردیناند موبیوس» (August Ferdinand Möbius) در سال ۱۸۳۲ میلادی معرفی شد. البته شباهت‌هایی بین نوشته‌های اویلر و نتایج موبیوس در این زمینه وجود دارد که باعث اختلاف در بین افرادی شده است که موبیس را مبدع این تابع معرفی کرده‌اند.

قبل از آنکه به تابع موبیوس بپردازیم، لازم است با مفهوم و اصطلاح  «ریشه‌های $$n$$ام واحد» ($$n$$th roots of unity) آشنا شویم زیرا تابع موبیس بر حسب این مقدار قابل محاسبه است.

ریشه nام واحد

عدد صحیح و مثبت $$n$$ را در نظر بگیرید. اگر مقدار صحیح (مثبت یا منفی) $$z$$‌ در معادله زیر صدق کند، آن را ریشه nام واحد ($$n$$th roots of unity) می‌نامند.

$$\large z^{n} = 1$$

رابطه ۱

واضح است که در رابطه ۱ $$n = 1,2,3,\ldots$$ است. همچنین مشخص است که مقدار $$z$$ ممکن است برابر با ۱ یا ۱- به ازاء $$n$$ زوج باشد. این دو مقدار را می‌توان به صورت اعداد مختلط با مقدار موهومی برابر صفر در نظر گرفت. به این ترتیب مقدار $$z$$ را به کمک رابطه زیر مشخص می‌کنیم.

$$\large {\displaystyle \exp \left({\frac {2k \pi i}{n}}\right) = \cos {\frac {2k\pi }{n}} + i \sin {\frac {2k \pi }{n}},\quad \quad k = 0,1,\dots ,n - 1}$$

رابطه ۲

ریشه nام واحد را اول (Primitive) گویند اگر هیچ ریشه $$n$$ام دیگری به ازاء $$k$$های کمتر از $$n$$ وجود نداشته باشد. به این ترتیب رابطه زیر برای ریشه $$n$$ام واحد اول (primitive nth roots of unity) مشخص می‌شود.

$$\large {\displaystyle z^{n} = 1 \quad {\text{ and }} \quad z^{k}\neq 1 {\text{ for }}k = 1, 2, 3, \ldots ,n-1}$$

رابطه ۳

نکته: اگر $$n$$ یک عدد اول باشد، آنگاه همه ریشه‌های واحد به جز ۱، اول خواهند بود. در رابطه ۳ مشخص است که $$n$$ و $$k$$ نسبت به یکدیگر «هم‌اول» (Coprime) یا متباین هستند.

در ادامه این متن، تعری و خصوصیات این تابع را در نظریه اعداد، مورد بررسی قرار خواهیم داد.

تعریف تابع موبیوس

تابع $$\mu(n)$$ را برای هر مقدار صحیح مثبت ($$n$$) به صورت مجموع «ریشه‌های $$n$$ام واحد اول» (primitive $$n$$th roots of unity) می‌شناسند.

با توجه به مطالب گفته شده در قسمت قبل، واضح است که مقدار این تابع در مجموعه $$\{-1,0,1\}$$ قرار می‌گیرد که بستگی به عوامل اول $$n$$ دارد. پس می‌توان تابع موبیوس را به صورت مجموع مقادیر ریشه‌های $$n$$ام واحد اول و به شکل زیر تعریف کرد.

$$\large { \displaystyle \mu (n)=\sum _{\stackrel {1\leq k\leq n}{\gcd(k,\,n)=1}}e^{2\pi i{\frac {k}{n}}}}$$

رابطه ۴

• اگر $$n$$ یک عدد مثبت صحیح نامربع (square-free) بوده و دارای یک عامل اول زوج (که می‌دانیم برابر با ۲ است) باشد، آنگاه مقدار تابع موبیوس $$\mu(n)$$ برابر است با ۱ ($$\mu(n)=1$$).
• اگر $$n$$ یک عدد مثبت با عوامل اول فرد باشد، مقدار تابع موبیوس $$\mu(n)$$ برابر با ۱- ($$\mu(n)=-1$$) خواهد بود.
• اگر $$n$$ دارای یک عامل اول مربع (Squared prime factor) باشد، مقدار تابع موبیوس $$\mu(n)$$ برابر با صفر است ($$\mu(n)=0$$).

به این ترتیب می‌توان تابع موبیوس را به صورت دیگری هم بیان کرد.

$$\large { \displaystyle \mu (n)\;=\;\delta _{ \omega (n)}^{ \Omega (n)} \; \lambda (n)}$$

رابطه 5

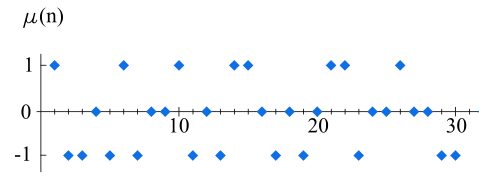
در اینجا $$\delta$$ تابع «دلتای کرونکر» (Kronecker delta function) بوده، $$\lambda(n)$$ هم «تابع لیوویل» (Liouville function) و $$\omega(n)$$ و $$\Omega(n)$$ نیز به ترتیب تعداد مقسوم‌علیه‌های اول $$n$$ و تعداد عامل‌های اول $$n$$ هستند. مقدارهای تابع $$\mu(n)$$ برای مقدارهای ۱ تا ۳۰ طبق جدول زیر است.

جدول ۱: ۳۰ مقدار اولیه تابع موبیوس

نمودار حاصل از این جدول نیز در تصویر زیر دیده می‌شود.

خصوصیات تابع موبیوس

با توجه به تعریفی که برای تابع موبیس ارائه شد، ویژگی و خصوصیات زیادی برای آن می‌توان در نظر گرفت که در ادامه به بعضی از آن‌ها اشاره خواهیم کرد.

فیلم آموزش مجموعه های مرتب و مشبکه ها (رایگان) در فرادرس

کلیک کنید

خاصیت ضربی بودن تابع موبیوس

یکی از خصوصیات جالب تابع موبیوس، «ضربی بودن» (Multiplicative) آن است. تابع $$f$$ را ضربی می‌نامند اگر رابطه زیر برای آن برقرار باشد.

$$\large f(ab) = f(a) f(b)$$

به این ترتیب می‌دانیم که تابع موبیوس نیز دارای خاصیت ضربی است، پس برای هر دو عدد متباین (نسبت به یکدیگر اول) داریم:

$$\large \mu(ab) = \mu(a) \mu(b)$$

این امر در جدول ۱ و همینطور نمودار مربوط به تصویر ۱ به خوبی دیده می‌شود. برای مثال اگر بخواهیم مقدار $$\mu(6)$$ را محاسبه کنیم، می‌توانیم از رابطه زیر استفاده کنیم.

$$\large 1 = \mu(6) = \mu(2 \times 3) = \mu (2) \times \mu(3) = -1 \times (-1) = 1$$

و همچنین برای $$\mu(18)$$ خواهیم داشت:

$$\large 1 = \mu(18) = \mu(2 \times 9) = \mu (2) \times \mu(9) = -1 \times 0 = 0$$

ولی توجه داشته باشید که این امر برای $$\mu(20)$$ به شکل زیر برقرار نخواهد بود. زیرا ۲ و ۱۰ نسبت به هم متباین نیستند.

$$\large 0 = \mu(20) = \mu( 2 \times 10) = \mu (2) \times \mu(10) = -1 \times (10) = 1$$

خاصیت مجموع تابع موبیوس

به یاد دارید که از نماد $$a|b$$ برای نشان دادن خاصیت  قابلیت شمرده شدن $$b$$ برحسب $$a$$ استفاده کردیم. به این معنی که حاصل تقسیم $$b$$ بر $$a$$ دارای باقی‌مانده صفر خواهد بود.

$$\large b \div a = q, q \in Z$$

واضح است که در رابطه بالا، منظور از $$Z$$، مجموعه اعداد صحیح است. حال این نماد را کمی گسترش می‌دهیم. در اینجا منظور از $$a|b$$ مجموعه همه اعداد صحیح مثبتی مثل $$a$$ است که $$b$$ را عاد کنند. برای مثال اگر $$b=10$$ باشد، آنگاه مقادیر که ۱۰ را عاد می‌کنند به صورت مجموعه زیر معرفی می‌شود.

$$\large a|10 = \{ 1 , 2 , 5 , 10\}$$

نکته: همانطور که می‌بینید، مقدار ۱ و خود ۱۰ نیز در این مجموعه قرار گرفته‌اند.

با توجه به این تعریف، یکی دیگر از خصوصیات تابع موبیوس را معرفی می‌کنیم. مقدار $$n$$ و $$d \leq n$$ که همگی صحیح مثبت هستند را در نظر بگیرید. به این ترتیب رابطه زیر برای مجموع مقادیر تابع موبیوس برای همه مقسوم‌علیه‌های مثبت $$n$$ که در اینجا با $$d$$‌ نشان می‌دهیم، برقرار است.

$$\large { \displaystyle \sum_{ d \mid n} \mu (d) = { \begin{cases}1 & { \text{ if }} n = 1 \\ \large 0 & {\text{ if }}n > 1\end{cases}}}$$

رابطه 6

این موضوع را به کمک جدول ۱ و همچنین نمودار ارائه شده در تصویر ۱ نیز می‌توان مشاهده کرد.

باز هم از $$n=6$$ و $$\mu(6)$$ استفاده می‌کنیم. می‌دانیم که مقسوم‌علیه‌های مقدار ۶ شامل مقادیر $$1,2,3,6$$ هستند. پس داریم:

$$\large \mu(1) + \mu(2) + \mu(3) + \mu(6) = 1 + (-1) + (-1) + 1 = 0$$

یا اگر $$n= 28$$ باشد، مقسوم علیه‌های آن شامل مقادیر $$1 ,2 , 4 , 7 , 14 , 28$$ خواهند بود. پس می‌توانیم رابطه مربوط به مجموعه مقادیر تابع موبیس برای آن‌ها را به صورت زیر بدست آوریم.

$$\large \mu(1) + \mu(2) + \mu(4) + \mu(7) + \mu(14)  + \mu(28) = 1 + (-1) + 0 + (-1) + 1 = 0$$

اثبات رابطه 6 براساس تعریفی که از تابع موبیوس در رابطه 2 دیدیم به سادگی مشخص می‌شود زیرا مجموعه $$n$$امین ریشه‌های واحد برابر با صفر است.

کاربردهای تابع موبیوس

یکی از کاربردهای تابع موبیوس، در تولید سری یا «دنباله دریکله» (Dirichlet Series) است. این دنباله مرتبط با معکوس تابع زتای ریمان (Riemann zeta function) است. فرض کنید $$s$$ یک عدد مختلط (Complex Number) با قسمت حقیقی (Real Part) برابر با ۱ باشد. آنگاه رابطه زیر برای سری یا دنباله دریلکه وجود دارد.

$$\large \sum_{n=1}^\infty \frac{\mu(n)}{n^s} = \frac{1}{\zeta(s)}$$

همچنین در «سری لامبرت» (Lambert Series) نیز ردپایی از تابع موبیوس دیده می‌شود. به ازای $$|q| <1$$ داریم:

$$\large { \displaystyle \sum_{ n=1 }^{\infty }{\frac {\mu (n) \; q^{n}}{1 - q^{n}}} = q}$$

همچنین برای اعداد اول بزرگتر از ۲ رابطه زیر هم برقرار است. در اینجا اعداد اول بزرگتر از ۲ را با $$\alpha$$ نشان داده‌ایم.

$$\large { \displaystyle \sum_{n=1}^{\infty } {\frac {\mu (\alpha n) q^{n}}{q^{n} - 1}} = \sum_{n \geq 0} q^{\alpha ^{n}},|q| < 1}$$

همچنین می‌توان نشان داد که مجموعه مقدارهای صحیح روی یک هذلولوی‌وار $$n$$ بُعدی (n-dimensional hyperboloids) برابر با مقدار تابع موبیوس $$n$$ است. به این ترتیب خواهیم داشت:

$$\large { \displaystyle { \underset {n>1}{\mu (n)}} = - { \underset {a=n} { \sum _{a\geq 2}}}1 + { \underset {ab = n}{\sum _{a\geq 2} \sum _{b\geq 2}}}1 - { \underset {abc = n}{\sum _{a\geq 2}\sum _{ b\geq 2}\sum _{ c\geq 2}}}1 + { \underset {abcd = n}{ \sum _{a\geq 2} \sum _{b\geq 2}\sum _{c\geq 2}\sum _{d\geq 2}}}1 - \cdots }$$

تعمیم تابع موبیوس

تابع موبیوس در جبر مدرن (Incidence Algebras) نیز به عنوان یکی از توابع مهم، تعمیم یافته و به کار گرفته می‌شود. همچنین «تابع پوپوویچی» (Popovici's Function) هم به نوعی تعمیم‌یافته تابع موبیس است که به شکل زیر و براساس ضرب یا «پیچش دریلکه» (Dirichlet convolution) نوشته می‌شود.

$$\large \mu_k(p^a) = (-1)^a \binom{k}{a} \$$

توجه داشته باشید که ضرایب دو جمله‌ای برای مقدارهای $$a>k$$ صفر خواهند بود.

نکته: ضرب دریکله در اینجا به صورت $$\mu_k = \mu * \mu \ldots *\mu$$ و به شکل زیر محاسبه می‌شود.

$$\large { \displaystyle (f*g)(n)\ =\ \sum _{d\,\mid \,n}f(d)\,g\!\left({\frac {n}{d}}\right)\ }$$

این تعریف را برای زمانی که $$k$$ یک عدد مختلط هم باشد می‌توان تعمیم داد به شرطی که ضرایب چندجمله‌ای را به جای ضرایب دوجمله‌ای در نظر بگیریم.

خلاصه و جمع‌بندی

در این نوشتار با تابع موبیوس و نحوه محاسبه آن آشنا شدیم. از آنجایی که دامنه این تابع مربوط به اعداد صحیح است، نقش مهمی در نظریه اعداد و همچنین توابع حسابی و ترکیبیات دارد. کاربردهایی از این تابع در فیزیک و مباحث مربوط به مدل‌سازی سیستم‌های دینامیکی و فیزیک کوانتم با استفاده از نظریه اعداد، معروف به «مدل آزاد پریمون» (Primon free model)، دیده می‌شود.

اگر این مطلب برای شما مفید بوده است، آموزش‌ها و مطالب زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• آموزش ساختمان گسسته با رویکرد حل مساله
• مجموعه آموزش‌های دروس رسمی دبیرستان و پیش‌دانشگاهی
• آموزش ریاضیات مهندسی
• قضیه اصلی حساب — به زبان ساده
• تقسیم عدد صحیح — به زبان ساده
• الگوریتم تقسیم اعداد — از صفر تا صد
• قواعد بخش پذیری یا عاد کردن — به زبان ساده

^^