اجتماع، اشتراک و تفاضل مجموعه ها – به زبان ساده
در مطالب قبلی وبلاگ فرادرس به بررسی انواع مجموعهها و بیان تعریف جامعی از آنها پرداخته شد. همانطور که بیان شد، یک مجموعه نشان دهنده همه اشیایی است که با یکدیگر صفتی مشترک دارند. بنابراین برای مشخص کردن یک مجموعه ابتدا نیاز به جمعآوری اشیایی داریم که در یک ویژگی بارز و مطلوب ما، تفاهم داشته باشند. این مطلب به بررسی اجتماع، اشتراک و تفاضل مجموعهها در ریاضیات میپردازد. در انتهای مطلب نیز تعارفی مانند مجموعه تهی و مجموعه جهانی مورد مطالعه قرار میگیرند.

تعریف مجموعه
همانطور که بیان شد، یک مجموعه شامل تعدادی ابزار، مواد، اعداد، اشیا و .. است که در ویژگی خاصی اشتراک داشته باشند.
برای مثال لباسهایی که شما میپوشید یک مجموعه را تشکیل میدهند. این مجموعه شامل جوراب، کفش، شلوار، پیراهن، تیشرت و سایر موارد است. برای مثال یک مجموعه شامل لباسهای مورد نیاز، در شکل زیر نشان داده شده است.

همانطور که در شکل بالا نشان داده شده، اعضای یک مجموعه را درون علامت آکولاد به شکل {} قرار میدهند. علاوه بر شکل بالا، مجموعه را میتوان به صورت حروف و اعداد نیز نمایش داد. برای مثال مجموعه لباسهایی که شما میپوشید را میتوان به فرم زیر نمایش داد.
{کفش، جوراب، پیراهن، شلوار و ...}
به عنوان یک مثال از مجموعههایی که با استفاده از اعداد بیان میشوند میتوان به مجموعه شامل تمام اعداد اشاره کرد که به صورت زیر نمایش داده میشوند.
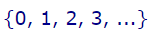
مثال دیگری از مجموعه اعداد، اعداد اول هستند. بنابراین مجموعه تمام اعداد اول را میتوان به شکل زیر نشان داد.
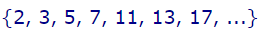
توجه کنید که این مثال را میتوان برای تمام مجموعه اعداد مانند مجموعه اعداد گویا، مجموعه اعداد حقیقی و مجموعه اعداد مختلط نیز به صورت دقیق مورد بررسی قرار داد.
در ادامه برای بررسی مفاهیم اجتماع، اشتراک و تفاضل مجموعهها مثالی از مجموعه چند دوست آورده میشود و مفاهیم مختلف را با استفاده از مجموعههای معرفی شده در این بخش، مورد مطالعه قرار میدهیم.
مجموعه دوستان
فرض کنید که یک مجموعهای شامل ده تا از بهترین دوستان شما را به شکل زیر بنویسیم.
البته شما میتوانید این اسامی را با نام بهترین دوستان خود عوض کنید و ادامه مطلب را با مجموعهای شامل نام دوستان خود به همراه ما ادامه بدهید!
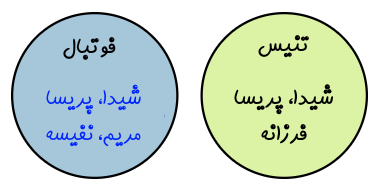
{شیدا، پریسا، مریم، نفیسه، صحاح، شقایق، الهه، پریا، فرزانه، محدثه}
هر یک از نامهای بالا به عنوان یک عضو از مجموعه دوستان ما شناخته میشوند. حال باید اشاره کنیم که چهار عضو این مجموعه دوستان شما، فوتبال بازی میکنند. این مجموعه را میتوان به شکل زیر نمایش داد.
فوتبال = {شیدا، پریسا، مریم، نفیسه}
مجموعه بالا اینگونه خوانده میشود؛ مجموعه فوتبال از چهار عضو به نامهای شیدا، پریسا، مریم و نفیسه تشکیل شدهاند. به صورت مشابه میتوان مجموعهای شامل دوستانی که تنیس بازی میکنند را نیز به شکل زیر نمایش داد.
تنیس = {شیدا، پریسا، فرزانه}
در واقع مجموعه تنیس از سه عضو به نامهای شیدا، پریسا و فرزانه تشکیل شده است.
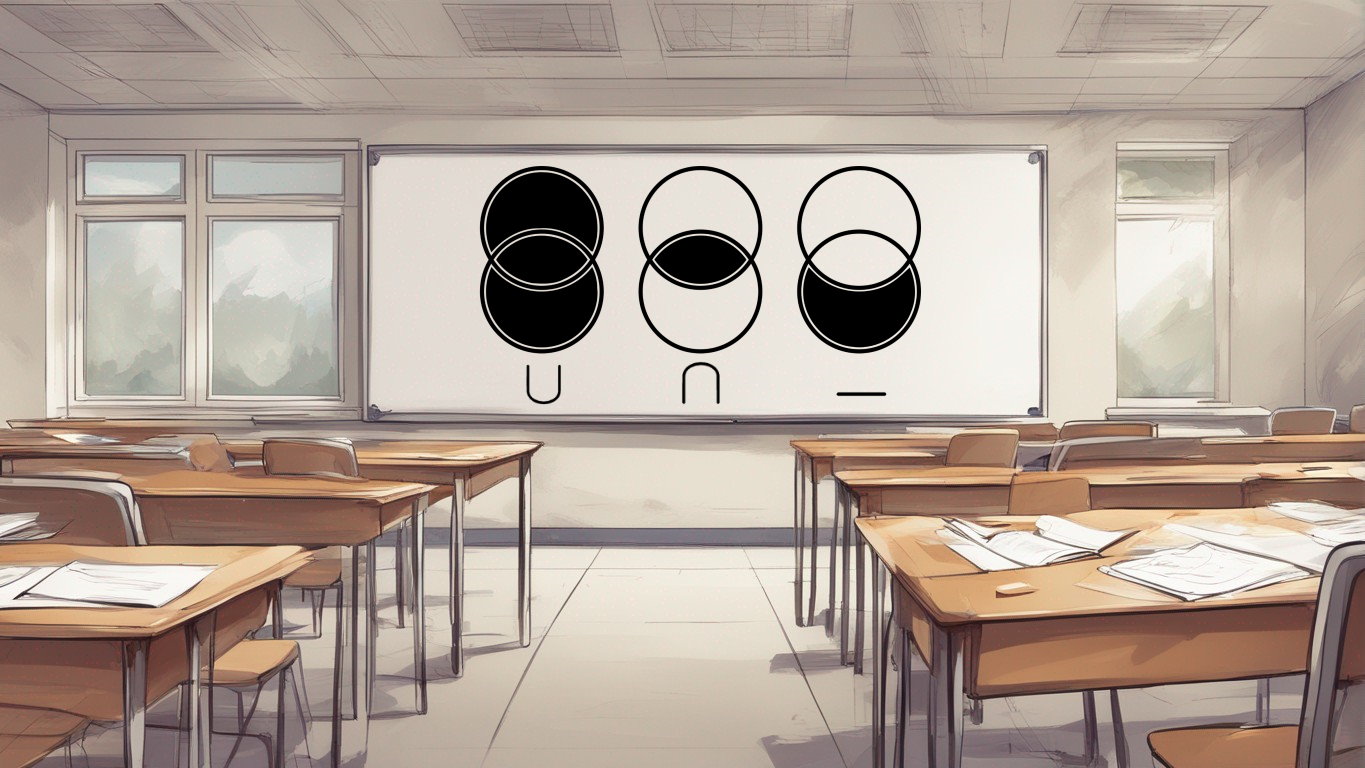
این دو مجموعه را میتوان به شکل زیر درون دو دایره نیز نمایش داد. این نمودار به «نمودار وِن» (Venn Diagram) یا نمودار مجموعه معروف است.
اجتماع
در این بخش، شما میتوانید لیستی از دوستان خود که فوتبال یا تنیس بازی میکنند را بیان کنید. توجه کنید که مهمترین عبارت در جمله قبل، عبارت «یا» است. در واقع مجموعه شامل فوتبال یا تنیس نشان دهنده «اجتماع» (Union) است و برای نمایش آن از نماد ریاضی ∪ استفاده میشود.
بنابراین با توجه به توضیحاتی که در بالا داده شد، مجموعه دوستانی که فوتبال یا تنیس بازی میکنند را میتوان به شکل زیر نمایش داد.
فوتبال ∪ تنیس = {شیدا، پریسا، فرزانه، مریم، نفیسه}
توجه کنید که همه افراد موجود در کره زمین در این لیست نیستند و این لیست تنها شامل دوستان شما است که فوتبال یا تنیس بازی میکنند. عبارت «یا» نشان میدهد که اسامی که در این لیست هستند سه حالت دارند. حالت اول فقط فوتبال بازی میکنند. حالت دوم فقط تنیس بازی میکنند. حالت سوم تنیس و فوتبال را همزمان بازی میکنند. این موضوع را با استفاده از نمودار ون یا نمودار مجموعه میتوان به شکل زیر نمایش داد.
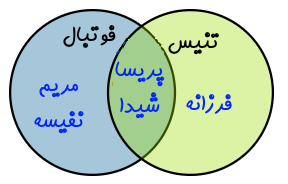
توجه کنید که نمودار ون یکی از بهترین شیوههای نمایش مجموعهها را در اختیار ما قرار میدهد و با استفاده از این نمودار میتوانیم بسیاری از سوالات مربوط به مجموعهها را به صورت دقیق مورد بررسی قرار دهیم.
با استفاده از این نمودار به راحتی میتوانید متوجه شوید که کدام یک از دوستان فقط فوتبال و کدامیک فقط تنیس بازی میکنند. همچنین دوستانی که هر دو ورزش تنیس و فوتبال را انجام میدهند نیز به راحتی قابل بیان هستند. تمام این اطلاعات از یک نمودار بسیار کوچک به دست میآید. در ادامه به بررسی سایر مفاهیم مانند اشتراک و تفاضل پرداخته میشود.
اشتراک
اشتراک حالتی را نشان میدهد که شما در هر دو مجموعه قرار دارید و یا در مثال بالا، اشتراک دوستانی را مشخص میکند که تنیس و فوتبال بازی میکنند. توجه کنید که مهمترین عبارت در جملات قبل «و» است. عبارت «و» نشان میدهد که ما به دنبال کسانی هستیم که به صورت همزمان فوتبال و تنیس بازی میکنند.
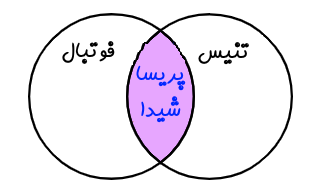
در مثال بالا شیدا و پریسا کسانی هستند که هم فوتبال و هم تنیس بازی میکنند. این حالت را اشتراک مینامند. اشتراک در ریاضیات با استفاده از نماد ∩ نشان داده میشود. اشتراک دو مجموعه معرفی شده یعنی مجموعه دوستانی که فوتبال بازی میکنند و مجموعه دوستانی که تنیس بازی میکنند را میتوان به شکل زیر نشان داد.
فوتبال ∩ تنیس = {شیدا، پریسا}
این مفهوم را میتوان با استفاده از نمودار ون نیز مورد مطالعه قرار داد. نمودار ون مربوط به اشتراک دو مجموعه فوتبال و تنیس به شکل زیر نشان داده شده است.
تفاضل
علاوه بر دو حالتی که در بالا معرفی شد یعنی اشتراک و اجتماع دو مجموعه، حالتی نیز حضور دارد که در آن تفاضل دو مجموعه را مورد مطالعه قرار میدهیم.
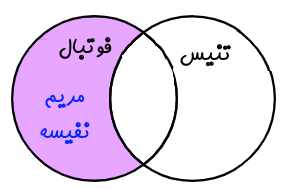
توجه کنید که با استفاده از تفاضل میتوان مجموعهای از دوستان را نشان داد که فوتبال بازی میکنند ولی تنیس بازی نمیکنند. برای به دست آوردن این مجموعه باید مجموعه فوتبال را منهای تنیس کرد یا به عبارت دیگر مجموعه تنیس را از مجموعه فوتبال کم کرد. این موضوع را میتوان با استفاده از رابطه زیر بیان کرد.
{مریم، نفیسه} = تنیس - فوتبال
این موضوع را میتوان با استفاده از نمودار ون نیز به شکل زیر بیان کرد.
بنابراین به صورت خلاصه میتوان بیان کرد که علامت ∪ نشان دهنده اجتماع دو مجموعه است و مجموعهای شامل اعضای هر دو مجموعه را نشان میدهد. همچنین ∩ نشان دهنده اشتراک دو مجموعه است و مجموعهای شامل اعضای مشترک بین دو مجموعه را نشان میدهد. مفهوم دیگری که بیان شد تفاضل دو مجموعه بود که با نماد - نشان داده شد و مفهوم آن در قالب مثال به صورت دقیق مورد بررسی قرار گرفت.
سه مجموعه
در ادامه، مفاهیم موجود در مجموعهها را برای حالتی که سه مجموعه حضور دارند مورد بررسی قرار میدهیم و نمودار وِن مربوط به آنها را با جزئیات بیان میکنیم.
در این بخش، مجموعه سوم شامل دوستانی هستند که والیبال بازی میکنند. این مجموعه به شکل زیر نمایش داده میشود.
والیبال = {شیدا، شقایق، فرزانه}
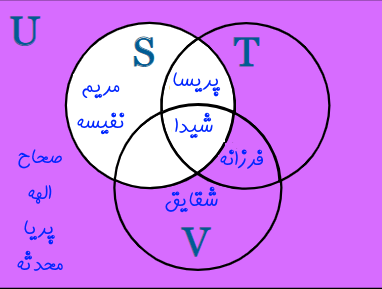
در ادامه و برای آنکه بتوانیم به شکل ریاضی، مجموعهها را بیان کنیم، به هر کدام از مجموعهها یک نام اختصاص میدهیم. مجموعه فوتبالیستها را با نماد S، مجموعه بازیکنان تنیس را با نماد T و مجموعه والیبالیستها را با نماد V نمایش میدهیم.
بنابراین با توجه به توضیحاتی بیان شده، نمودار وِن این سه مجموعه به شکل زیر نمایش داده میشود.
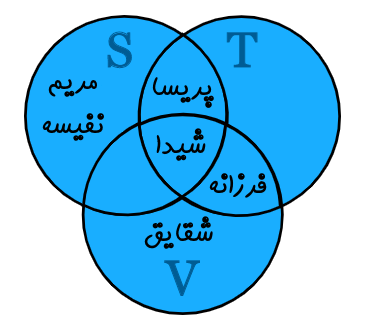
با استفاده از این نمودار میتوان دریافت که شیدا کسی هست که فوتبال، والیبال و تنیس بازی میکند. فرزانه تنیس و والیبال بازی میکند. همچنین مریم و نفیسه تنها فوتبال بازی میکنند و ورزشهای والیبال و تنیس را انجام نمیدهند. نکته دیگری که از نمودار بالا میتوان دریافت این است که هیچ فردی وجود ندارد که فقط ورزش تنیس را انجام دهد.
در ادامه با استفاده از مفهوم اشتراک و اجتماع به صورت دقیق به بررسی این سه مجموعه پرداخته میشود.
به عنوان اولین مثال، اشتراک دو مجموعه فوتبال و والیبال را بررسی میکنیم که میتوان این مجموعه را به شکل زیر نمایش داد.
{شیدا} = S ∩ V
این موضوع را میتوان به کمک نمودار وِن نیز به شکل زیر نمایش داد.
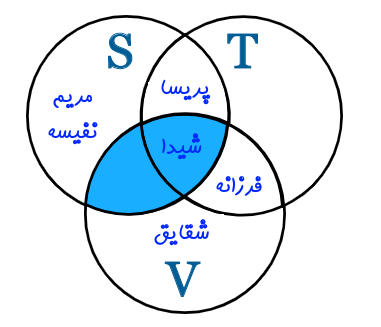
همانطور که مشاهده میشود، فهم دقیق اجتماع، اشتراک و تفاضل این مجموعهها به کمک نمودار ون به سادگی انجام میشود و توصیه ما رسم این نمودار در مثالهای مختلف برای فهم دقیق مسئله است. همچنین اجتماع دو مجموعه والیبال و تنیس را نیز میتوان به شکل زیر نمایش داد.
{شقایق، فرزانه، شیدا، پریسا} = T ∪ V
در ادامه و به عنوان یک مثال پیشرفته، مجموعه بازیکنان تنیس را از اشتراک دو مجموعه فوتبال و والیبال کم کنید. برای این منظور ابتدا اشتراک دو مجموعه فوتبال و والیبال را محاسبه میکنیم. این مورد در قسمت قبل به شکل زیر محاسبه شد.
{شیدا} = S ∩ V
در ادامه مجموعه دوستانی که تنیس بازی میکنند را از این مجموعه کم میکنیم. این مجموعه را میتوان به شکل زیر با استفاده از نمودار ون نمایش داد.
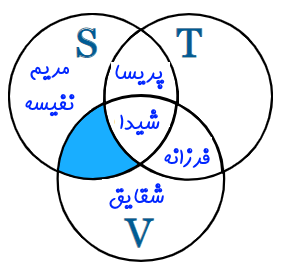
شیوه نمایش ریاضی این مجموعه نیز به شکل زیر است.
{ } = S ∩ V) - T)
بنابراین همانطور که در شکل و عبارت بالا مشاهده میشود، مجموعه بالا شامل هیچ عضوی نیست. این مجموعه را مجموعه تهی مینامند. و آن را با نماد { } نمایش میدهند.
مجموعه جهانی
مجموعه جهانی، مجموعهای است که تمام اعضایی که برای ما مورد اهمیت هستند را در بر میگیرد. توجه کنید که این مجموعه را با نماد U نشان میدهند و شما باید احتیاط کنید که حرف U را با نماد ∪ (اجتماع دو مجموعه) اشتباه نگیرید.
در ادامه مثالی که در ابتدای این مطلب بیان شد را در نظر بگیرید. مجموعه جهانی در این مثال شامل بهترین دوستان شما هستند. این مجموعه جهانی را میتوان به شکل زیر نمایش داد.
{شیدا، پریسا، مریم، نفیسه، صحاح، شقایق، الهه، پریا، فرزانه، محدثه} = U
نمایش مجموعه جهانی در نمودار وِن با استفاده از یک مستطیل اطراف مجموعهها انجام میشود. این موضوع در شکل زیر به خوبی به تصویر کشیده شده است.
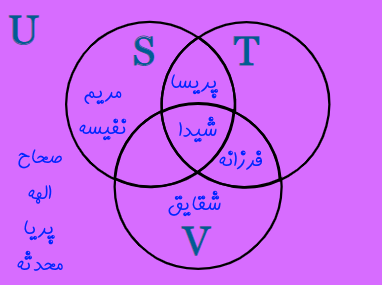
بنابراین با استفاده از مجموعه جهانی، شما تمام ۱۰ دوست صمیمی خود (شامل دوستانی که ورزش میکنند و یا آنهایی که ورزش نمیکنند) را مشاهده میکنید.
عملیات مختلف مجموعهها شامل اجتماع، اشتراک و تفاضل مجموعهها را میتوان روی مجموعه جهانی نیز اجرا کرد. برای مثال مجموعه دوستانی که فوتبال بازی میکنند را از مجموعه جهانی کم کنید. این موضوع به شکل زیر نمایش داده میشود.
{صحاح، شقایق، الهه، پریا، فرزانه، محدثه} = U - S
توجه کنید که این مجموعه را میتوان به دو صورت بیان کرد. حالت اول این است که U - S را به فرم مجموعه جهانی منهای مجموعه دوستان فوتبالیست بیان کنیم و حالت دوم این است که U - S را برابر با همه دوستانی که فوتبال بازی نمیکنند، در نظر بگیریم. هر دو این حالات یک معنا را نشان میدهند و با یکدیگر برابر هستند.
این مجموعه را با استفاده از نمودار ون نیز میتوان به سادگی و مطابق با شکل زیر بیان کرد.
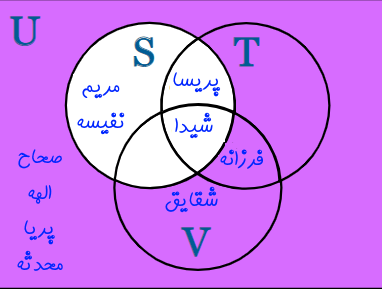
متمم یک مجموعه
متمم یک مجموعه نیز یکی از تعاریف مهم در مجموعهها است. برای مثال متمم مجموعه S نشان دهنده تمام اعضایی است که عضو مجموعه جهانی هستند و درون مجموعه S قرار نمیگیرند.
در این مثال متمم مجموعه S، تمام دوستان صمیمی شما که فوتبال بازی نمیکنند را نشان میدهد (توجه شود که S مجموعه دوستان صمیمی شما است که فوتبال بازی میکنند).
متمم را با استفاده از نماد C در بالای مجموعه نیز نمایش میدهند. برای مثال متمم مجموعه S را به شکل زیر میتوان نمایش داد.
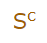
همانطور که بیان شد، نماد بالا نشان دهنده تمام اعضایی است که عضو مجموعه S نباشند. اگر مجموعه S را دوستانی که فوتبال بازی میکنند در نظر بگیریم، مجموعه متمم S را میتوان با استفاده از نمودار ون به شکل زیر نمایش داد.
شیوه نمایش این اعضا نیز به شکل زیر است.
{صحاح، شقایق، الهه، پریا، فرزانه، محدثه} = U - S
نکته بسیار مهمی که باید به آن اشاره کرد این است که متمم مجموعه S، دقیقا برابر با تفاضل مجموعه S از مجموعه جهانی است که با نماد U - S نمایش داده میشود.
بنابراین به صورت خلاصه میتوان بیان کرد که اجتماع با نماد ∪ نشان داده میشود و اجتماع دو مجموعه، اعضای هر دو مجموعه را در بر میگیرد. همچنین میتوان نشان داده که ∩ اشتراک دو مجموعه را بیان میکند و تنها شامل اعضایی است که در هر دو مجموعه حضور داشته باشند.
علاوه بر اجتماع و اشتراک، تفاضل و متمم نیز دو مفهوم کلی و مهم در مورد مجموعهها هستند. تفاضل را با نماد - نمایش میدهند و تفاضل دو مجموعه شامل اعضایی است که در یکی از این مجموعهها وجود دارند ولی در دیگری حضور ندارند. متمم نیز مفهوم بسیار مهمی در مجموعهها را نشان میدهد. متمم مجموعه S شامل تمام اعضایی است که عضو مجموعه S نیستند.
نکته دیگری که در این مطلب به صورت دقیق مورد بررسی قرار گرفت، تعریف دو مجموعه تهی و جهانی است. مجموعه تهی، مجموعهای است که در آن هیچ عضوی وجود ندارد و با نماد { } نشان داده میشود. مجموعه جهانی نیز شامل مجموعهای است که تمام اعضای دلخواه ما (مثلا تمام دوستان صمیمی) را در بر میگیرد.
آزمون اجتماع، اشتراک و تفاضل مجموعه
۱. کدام ویژگی اساسی باعث میشود مجموعه یک مفهوم ریاضی ویژه باشد، نه صرفا یک گروه اشیا؟
اعضای مجموعه همگی از یک جنس فیزیکیاند.
اعضای مجموعه دارای یک ویژگی مشترک هستند.
در مجموعه فقط اعداد قرار میگیرند.
مجموعه همیشه به صورت تصویری نمایش داده میشود.
تعریف مجموعه بر ویژگی مشترک اعضا استوار است، یعنی هر عضو با دیگر اعضا یک صفت روشن و مشخص مشترک دارد. بنابراین، عبارت «اعضای مجموعه دارای یک ویژگی مشترک هستند» تعریف دقیق مفهوم مجموعه را بازگو میکند. عضوهای یک مجموعه الزاما همگی از یک جنس فیزیکی نیستند و میتوانند اعداد یا لباس باشند، پس «اعضای مجموعه همگی از یک جنس فیزیکیاند» درست نیست. همچنین مجموعه محدود به اعداد نیست و اشیای مختلف را میتواند شامل شود، بنابراین «در مجموعه فقط اعداد قرار میگیرند» نادرست است. در نهایت، نمایش مجموعه فقط تصویری نیست و روشهای نوشتاری و آکولادی هم وجود دارد، پس گزینه «مجموعه همیشه به صورت تصویری نمایش داده میشود» نیز توضیحی صحیح از ویژگی ذاتی مجموعه نیست.
۲. در نمودار ون، آنچه تفاوت اساسی میان نمایش اجتماع و اشتراک دو مجموعه را نشان میدهد چیست؟
اجتماع همه اعضای هر دو مجموعه را حتی اگر مشترک نباشند، شامل میشود اما اشتراک فقط اعضای مشترک را در بر میگیرد.
اجتماع اعضای تهی را نشان میدهد، اشتراک همه اعضای بیرون مجموعهها را.
در اجتماع نماد ∩ به کار میرود اما در اشتراک نماد ∪ استفاده میشود.
اجتماع تنها بر یک مجموعه تمرکز دارد، ولی اشتراک همزمان هر دو مجموعه را در نظر میگیرد.
در نمودار ون، «اجتماع همه اعضا از هر دو مجموعه را حتی اگر مشترک نباشند، شامل میشود»، در حالی که «اشتراک فقط اعضایی را در نظر میگیرد که همزمان در هر دو مجموعه حضور دارند». این تفاوت بر نمایش تصویری نیز تاثیر دارد: ناحیه اجتماع ترکیب کل هردو مجموعه است اما ناحیه اشتراک تنها بخش مشترک بین آنهاست. عباراتی مانند تمرکز بر یک مجموعه یا نمایش اعضای تهی، مطابق توضیحات داده شده درباره اجتماع و اشتراک نیستند، و نماد ∪ متعلق به اجتماع و ∩ به اشتراک مربوط است، نه برعکس. بنابراین تنها جمله مربوط به «در بر گرفتن همه اعضا در اجتماع و فقط اعضای مشترک در اشتراک» دقیق است.
۳. اگر A مجموعه دوستان فوتبالیست و B مجموعه دوستان تنیسباز باشد، اعضای فقط فوتبالیست با چه نمادی نشان داده میشوند؟
A – B
A ∩ B
B – A
A ∪ B
عبارت "A – B" نشاندهنده تمام اعضای مجموعه A است که در مجموعه B حضور ندارند. یعنی دوستانی که فقط فوتبالیست هستند و تنیس بازی نمیکنند. نماد "A ∪ B" اجتماع را نشان میدهد و همه فوتبالیستها یا تنیسبازها را شامل میشود. "A ∩ B" فقط مربوط به اعضای مشترک یعنی کسانی است که هر دو ورزش را انجام میدهند. "B – A" هم فقط دوستان تنیسبازِ بدون عضویت در فوتبالیستها را نشان میدهد. بنابراین "A – B" نماد صحیح برای یافتن فوتبالیستهایی است که تنیس بازی نمیکنند.
۴. فرض کنید سه مجموعه S، T و V به ترتیب نشاندهنده فوتبال، تنیس و والیبال باشند. اگر عضوی فقط در دو ورزش عضو باشد، محل نمایش این عضو در نمودار ون چگونه خواهد بود؟
در محدوده جدا از هر سه دایره
در ناحیه اشتراک دو دایره متقاطع و خارج از سومی
در مرکز مشترک هر سه دایره
در داخل تنها یکی از دایره ها
عضوی که فقط در دو ورزش عضو است، دقیقا در بخشی از نمودار ون قرار میگیرد که دو دایره از سه دایره را به هم متصل میکند اما با دایره سوم اشتراکی ندارد. پس ناحیه مربوط به اشتراک دو دایره و خارج از سومی محل مناسب اوست.
۵. مجموعه جهانی در کار با مجموعهها چه جایگاهی دارد و چگونه از نماد اجتماع متمایز میشود؟
مجموعه جهانی فقط برای مجموعه تهی تعریف میشود و نماد آن ∅ است.
مجموعه جهانی تمام اعضای قابل بررسی را شامل است و نماد آن U است، نه ∪.
مجموعه جهانی شامل فقط اعضای یک مجموعه خاص است و نمادش ∪ است.
مجموعه جهانی فقط اعضای مشترک همه مجموعهها را نشان میدهد و نماد آن ∩ است.
عبارت «مجموعه جهانی تمام اعضای قابل بررسی را شامل است و نماد آن U است، نه ∪» صحیح است، زیرا مجموعه جهانی (Universal Set) تمام عناصر دامنه مورد بررسی را دربرمیگیرد و حرف بزرگ U برای نمایش آن به کار میرود. نماد ∪ مخصوص عمل اجتماع (Union) است که تنها عناصر دو یا چند مجموعه را بدون تکرار گردآوری میکند و با U که مجموعه جهانی را نشان میدهد، تفاوت دارد.
۶. برای تعیین اعضایی که در مجموعه جهانی هستند اما عضو مجموعه S نمیباشند، چه عملی انجام میشود و با چه نمادی نمایش داده میشود؟
از اجتماع با نماد ∪ بهره میگیریم و همه اعضای هر دو مجموعه را در نظر میگیریم.
از متم با نماد 'S' یا S' استفاده میکنیم و اعضای بیرون S در مجموعه جهانی را به دست میآوریم.
از تفاضل با نماد – استفاده میکنیم و فقط اعضای S را حذف میکنیم.
از اشتراک با نماد ∩ استفاده میکنیم تا فقط اعضای مشترک پیدا شوند.
برای یافتن اعضایی که در مجموعه جهانی حضور دارند اما عضو مجموعه S نیستند، باید عمل متمم را انجام داد که با نماد 'S' یا S' نمایش داده میشود. این عمل دقیقا اعضای بیرون مجموعه S را نسبت به مجموعه جهانی مشخص میکند. اجتماع و اشتراک فقط اعضای کلی یا مشترک را مییابند و با هدف حذف یا جدا کردن اعضا کار نمیکنند. تفاضل اگرچه اعضای S را حذف میکند، اما معمولا به شکل U – S برای این هدف، نه مستقیما با نماد خاص متمم. بنابراین، تعریف و نماد «متمم» تنها راه درست برای شناسایی اعضای خارج از S نسبت به مجموعه جهانی است.












توی تفاضل باید کدومو منهای کدوم کنیم استاد
با سلام خدمت شما؛
در عبارت A – B همواره A مجموعه اصلی و B مجموعهای است که از آن کم میشود.
از همراهی شما با مجله فرادرس سپاسگزاریم.
= جواب چند میشه
لطفا جواب بدین'(A-B)
سلام دوتا لینک آخر خرابن
@Sara
توی مورد اول، برای اثبات اینکه B-(A-B)=B، یکی از راههاش اینه که دو گزارهٔ زیر رو ثابت کنیم:
۱. B-(A-B)⊆B
۲. B⊆B-(A-B)
برای اثبات هر دو، از عضوگیری دلخواه استفاده میکنیم. برای اثبات گزارهٔ ۱، فرض میکنیم که x عضوی از B-(A-B) باشه. پس طبق تعریف تفاضل، x عضو B هست ولی عضو A-B نیست. درنتیجه x هم عضو B هست و هم عضو متممِ A-B. پس طبق قانون حذف عاطف، x عضو B هست و گزارهٔ ۱ ثابت شد. اما گزارهٔ ۲. فرض میکنیم که x عضوی از B باشد. پس طبق قانون ادخال فاصل، x عضو B هست یا x عضو A نیست. پس در نتیجه x عضو B هست یا x عضو A نیست و x عضو B هست. حالا اگر x عضو A-B باشه، یعنی x عضو A هست و عضو B نیست که تناقضه بهخاطر اینکه گفتیم که x عضو B هست یا x عضو A نیست. پس x عضو A-B نیست. پس x عضو B هست و x عضو A-B نیست گزارهای درسته و یعنی x عضو B-(A-B) است و حکم کلاً ثابت شد.
اما مورد دوم. مورد دوم رو در واقع میشه اینجوری نوشت:
A⊆B → A∩B’=⍉
فرض کنید که ‘A∩B برابر با تهی نباشد. پس عضوی مثل x وجود دارد که هم عضو A هست و هم عضو ‘B. پس یعنی x عضو A هست ولی عضو B نیست که یعنی A زیرمجموعهٔ B نیست که تناقضه. پس فرض خلف باطل و حکم ثابت شد.
سلام
میشه این دو مثال رو اثبات کنید:
1. B-(A-B)=B
2. A زیرمجموعه B انگاه A اشتراکش با Bپریم مساوی است با تهی
عالی بود خسته نباشید
اون جوابی ک من میخواستم رو نداشت
مرس
برای سه مجموعه ی دلخواه AوBوC، تعداد اعضای مجموعه های ، A_B,B_C,A_C,C_A,C_Bبه ترتیب برابر با ۴،۷،۵،۶،۴ می باشد. تعداد اعضای B_Aچندتا است؟
سلام وقت بخیر واقعا خیلی کامل و جامع توضیح میدهید خیلی خیلی خسته نباشید واقعا ممنون
سلام
اگر در اجتماع دو بازه در هر بازه یه عدد مشترک باشه اونوقت اون عدد رو از جواب بدست اومده کم میکنیم؟
مثال:(۲،۳) [-۴,۳]
بین اینا اجتماع باشه البته اگه اشتراک یا تفاضل باشه اونوقت فرقی میکنه؟
اگر P(A)+P(B)=1.8 باشد. حداکثر مقدار P(A ́∩B ́ )را بدست آورید.
سلام یه سوال داشتم
مجموعهaراباعلائم ریاضی نشان دهید.
(…و۵۵۵۵و۵۵۵و۵۵وA=(5
وقتی درجواب تعداد عضو های یک مجموعه ای رو بخواد باید عدد جواب را داخل یک مجموعه قرار بدیم یا به طور معمولی عدد روبنویسیم؟
درود بر شما همراه فرادرس؛
اگر از جنبه محاسباتی این دنباله را در نظر بگیریم، میتوانیم رابطه زیر را برای اجزای آن بنویسیم.
x_i+1 = 5 * 10^i + x_i
i = 0 , 1, , x_0 = 0
به این ترتیب یک رابطه بازگشتی برای این دنباله نوشته شد.
پیروز و سربلند باشید.
سلام خسته نباشید اجتماع هر مجموعه با مجموعه تهی برابر با خود مجموعه هست پس اجتماع هر مجموعه با متمم تهی جوابش چی میشه؟
خود مجموعه مورد نظر
سلام بر شما خواننده گرامی،
اگر مطلب را با دقت خوانده باشید، میدانید که متمم یک مجموعه وابسته به مجموعه مرجع است. پس متمم مجموعه تهی، همان مجموعه مرجع را خواهد ساخت. بنابراین اجتماع هر مجموعهای با مجموعه مرجع، چیزی به آن اضافه نمیکند و برابر با مجموعه مرجع خواهد بود.
از این مشکلاتتان را با ما مطرح میکنید، خرسندیم.
مشتاقانه منتظر نظرات و پیشنهاداتتان هستیم.
تندرست و پیروز باشید.
سلام یک سوال داشتم جواب این سوال چی میشه
A اجتماع(A اشتراک B) بدون هیچ عددی
جواب سوال
ZاشتراکN
چی میشه؟
سلام.
اشتراک مجموعه اعداد طبیعی و اعداد صحیح، مجموعه اعداد طبیعی است.
سالم و موفق باشید.
درود بر شما خواننده گرامی؛
برای پاسخ به سوال شما به این نکته اشاره میکنیم که منظور از A اشتراک B، همه اعضایی از هر دو مجموعه است که با هم مشترک هستند. مسلما این اشتراک زیر مجموعهای از A است.
همچنین اجتماع A با هر زیرمجموعهای از خودش، مجموعه A را تشکیل میدهد. پس پاسخ سوال شما مجموعه A خواهد بود.
تندرست و پیروز باشید.
سلام.اشتراک مجموعه های نامتناهی بااثبات میشه بگید چی میشه
سلام و درود؛
سوال شما پاسخی ندارد. اشتراک مجموعههای نامتناهی بدون آنکه از ماهیت و خصوصیات آنها مطلع باشیم، مجموعه مشخصی نمی شود.
برای مثال مجموعه نامتناهی اعداد طبیعی با مجموعه نامتناهی اعداد صحیح اشتراکی به صورت مجموعه نامتناهی اعداد طبیعی دارد. ولی اشتراک مجموعه اعداد حقیقی و مجموعه اعداد اصم، اشتراکی به صورت مجموعه اعداد اصم دارد.///
ولی شاید سوال شما در مورد دنبالهای از مجموعههای نامتناهی باشد که به صورت زیر مجموعه هستند. A_i ها را یک دنباله از مجموعههای نامتناهی در نظر می گیریم که به صورت صعودی مرتب شده اند یعنی A_i زیر مجموعه Ai+1 است. در این حالت اشتراک آنها A1 یا اولین مجموعه خواهد شد که زیر مجموعه همه Ai ها است.
لطفا سوال خود را دوباره مرور کنید و با دقت آن را مطرح فرمایید.
موفق باشید.
درچه حالتی اجتماع دو مجموعه با تفاضل آن برابر میشود؟
سلام بر شما همراه مجله فرادرس،
در پاسخ به سوال شما باید ابتدا مجموعهها را به صورت نمادین مشخص کنیم اگر دو مجموعه را به صورت A و B در نظر بگیریم آنگاه اجتماع و تفاضل آنها را به صورت زیر نشان میدهیم.
A∪B و A–B. در این صورت زمانی این دو مجموعه با یکدیگر برابر هستند که داشته باشیم:
A∪B=A–B یا به طور مشابه A∪B–(A–B)=∅
بنابر قضیه دمورگان با استفاده از رابطه بالا، خواهیم داشت:
(A∪B)∩(A–B)’=(A∪B)∩(A’∪B)=B∪(A∩A’)=B
که باید با مجموعه تهی برابر باشد، بنابراین تساوی فقط زمانی که مجموعه B تهی باشد، برقرار است.
البته به کمک نمودار ون در سه حالت مختلف (وجود اشتراک، جدا بودن و زیر مجموعه بودن مجموعه B با A نیز میتوان به صورت شهودی تساوی را مورد بررسی قرار داد.
از اینکه همراه مجله فرادرس هستید، بسیار سپاسگزاریم.
سلام
چرا اسم این مجموعه ها رو متمم گذاشتند؟؟؟
دلیلش چیع؟؟
سلام خسته نباشید و ممنون از سایت خوبتون
از ما خواسته شده پاسخ عبارت (3,4]∩(0,1) رو ب صورت بازه بنویسیم.
خب اینها چون اشتراکی باهم ندارن همون مجوعه تهی رو مینویسم یا به نحو ديگهای ؟
سلام وقت بخیر
ببخشید R_N برابر با چی میشه؟
سلام،خسته نباشید.
من میخواستم بدونم ک اشتراک یک مجموعه با خودش چند میشه؟
خودش میشه
سلام و وقت بخیر
واضح هست که تمامی اعضای یک مجموعه در خود مجموعه هست. در نتیجه اشتراک یک مجموعه با خودش برابر با همان مجموعه خواهد بود.
از اینکه همراه مجله فرادرس هستید خرسندیم.
موفق و تندرست باشید.
سلام وقتتون بخیر سوال من اینکه اگر دو بازه هیچ اشتراکی نداشته باشند و بخواهیم اجتماع انها را محاسبه کنیم جواب چه خواهد بود
مثل:(4و3) (3و4-) نمیتونیم اجتماع بگیریم؟
سلام و درود بر شما خواننده گرامی،
اگر دو مجموعه هیچ اشتراکی نداشته باشند، حاصل احتمال آنها، مجموعهای است که از هر دو آنها تشکیل شده است. در مثال شما نیز همین حالت پیش آمده و اجتماع این دو مجموعه (فاصله اعداد) به صورت زیر خواهد بود.
(−4,4)–{3} یعنی بازه از ۴- تا ۴ بدون مقدار ۳. البته این بازه را به صورت (−4,3)∪(3,4) نیز می توان نشان داد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
پیروز و تندرست و شاد باشید.
سلام ببخشید
می خواستم بدونم که مثلا مجموعه a
aاشتراک مجموعه تهی یا aاجتماع مجموعه تهی جوابشون چی میشه لطفا جواب بدین
سلام بر همراه مجله فرادرس،
اشتراک هر مجموعهای با مجموعه تهی برابر با مجموعه تهی است.
از طرفی اجتماع هر مجموعه با مجموعه تهی، خود مجموعه خواهد بود.
موفق و تندرست باشید.
اعداد حقیقی منهای تهی چند می شود
R_تهی
سلام میشه جواب این سوال رو بگین
در یک بررسی اماری در استفاده از رادیو و تلویزیون و رایانه از 90نفر این نتایج به دست امده 12 نفر فقط از رادیو 15 نفر فقط از تلویزیون 23 نفر فقط از رایانه 14 نفر از رادیو و تلویزیون 19 نفر تلویزیون و رایانه 18 نفر رادیو و رایانه استفاده میکنند 7 نفر هم از هیچ کدام استفاده نمیکنند چند نفر از هر سه مورد استفاده میکنند ؟ با نمودار وِن و مجموعه
سلام روز بخیر
جواب (AUB)اشتراک با A
عالیییی ??
سلام اون چیزی که میخواستم رو نداشت
اشتراک سه مجوعه عددی را چگونه بدست اوریم
عای بهترین با هی بار خوندت همه رو فهمیدم??❤?
سلام ی سوالی داشتم میگم تفاضل دو مجموعه چه زمانی با هم برابر است
با سلام و تشکر از همراهی شما با فرادرس
برای پاسخ به سوال شما، رابطه تساوی را برای دو مجموعه A و B مینویسیم.
A−B=B−A این تساوی زمانی برقرار است که تفاضلها مجموعه تهی باشند یعنی هیچ کدام از مجموعهها با متمم مجموعه دیگری اشتراک نداشته باشد.
A∩B’=B∩A’=∅
از اینکه همراه فرادرس هستید سپاسگزاریم