واپاشی پرتوزا (Radioactive Decay) – به زبان ساده

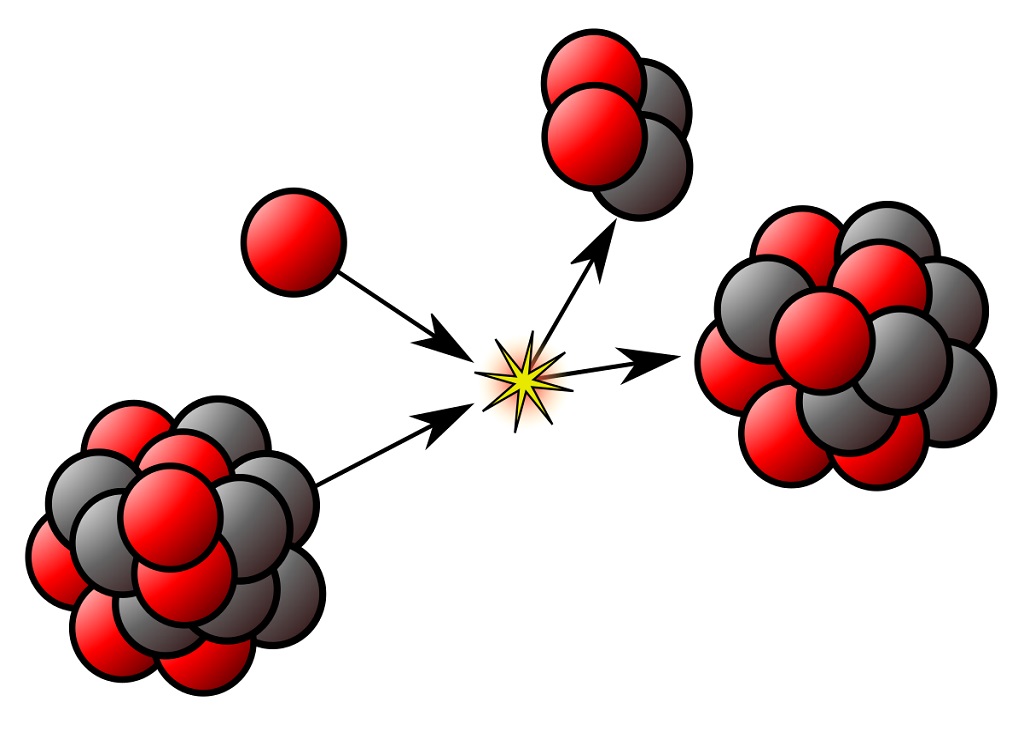
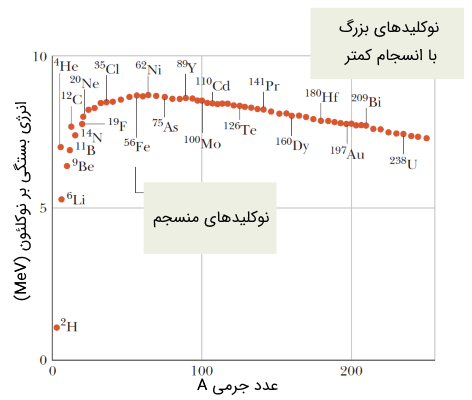
در مقاله «هسته اتم یا نوکلید (Nuclide) -- به زبان ساده» با تعریف و مفهوم هسته اتم یا همان نوکلید‌ها (نوکلئید - nuclide) آشنا شدیم. همچنین دیدیم که اکثر نوکلیدها ناپایدار بوده که اصطلاحاً آن‌ها را رادیونوکلید می‌نامند. به عبارت دیگر، نوکلیدها دارای واپاشی پرتوزا (Radioactive Decay) هستند. در مقاله مذکور، همچنین با نمودار زیر که انرژی بستگی بر نوکلئون بر مبنای عدد جرمی $$A$$ را نشان می‌دهد، آشنا شدیم.

در مقاله «نیمه عمر — به زبان ساده» نیز، با روند ریاضی به دست آوردن رابطه محاسبه نیمه عمر آشنا شدیم. در این مقاله در نظر داریم تا با زبانی ساده بیشتر به مفهوم واپاشی پرتو و ارتباط آن به نیمه عمر بپردازیم.

واپاشی پرتوزا

همان‌طور که از نمودار فوق مشخص است، اکثر نوکلید‌ها پرتوزا هستند. نوکلیدهای ناپایدار (رادیونوکلیدها) می‌توانند به طور کاملاً تصادفی در لحظه، ذره‌ای را گسیل (تابش) کرده و به نوکلید دیگری تبدیل شوند. از آنجایی که عمل واپاشی پرتوزا برای نوکلیدها به صورت تصادفی رخ می‌دهد، می‌توان قوانین فیزیکی مربوط به فرآیندهای زیراتمی (هسته‌ای) را در دسته فیزیک آماری قرار داد.

به طور مثال، در نمونه‌ای یک گرمی از فلز اورانیوم که شامل $$2.5 \times 10^{18}$$ نوکلید پرتوزای $$^{238} U$$ با طول عمر بالا است، تنها در حدود ۱۲ هسته (نوکلید) در ثانیه‌ای معین با گسیل ذره آلفا (نوکلید هلیوم/ هیلوم دوبار مثبت) به نوکلید $$^{234} Th$$ تبدیل می‌شوند. در دنیای فیزیک هسته‌ای از این دست مثال‌ها فراوان یافت می‌شود.

با این اوصاف، به طور قطع، نمی‌توان پیشگویی کرد که در یک زمان مشخص، کدام هسته یا نوکلید در جرم مشخصی از ماده دچار واپاشی پرتوزا می‌شود. به عبارت دیگر، تمامی نوکلیدها در یک نمونه، دارای احتمال یکسان جهت واپاشی پرتوزا هستند.

آهنگ واپاشی نوکلیدها

با توجه به مطلب فوق، حدس زدن فرآیند واپاشی پرتوزا برای یک نوکلید در جرمی (نمونه‌ای) با تعداد رادیونوکلیدهای مشخص، غیر ممکن است. ولی می‌توان گفت که اگر نمونه دارای $$N$$ هسته پرتوزا یا رادیونوکلید باشد، آهنگ واپاشی نوکلید‌ها در زمان را می‌توان توسط ثابت تناسبی به $$N$$ مربوط کرد. یعنی:

$$\large - \frac{ d N }{ d t } = \lambda N$$
(1)

در رابطه فوق، λ ثابت تناسب بوده که به ثابت فروپاشی (disintegration constant) یا ثابت واپاشی (decay constant) معروف است. یکای ثابت واپاشی در سیستم بین‌المللی $$SI$$ معکوس ثانیه ($$\frac{ 1 }{ s } = s^{ - 1 }$$) است.

جهت تعیین $$N$$، یعنی تعداد رادیونوکلیدهای یک نمونه پرتوزا، می‌توانیم معادله (۱) را به صورت زیر بازنویسی کرده و سپس از دو سمت آن انتگرال بگیریم. به عبارت دیگر قصد داریم تا $$N$$ را به صورت تابعی از زمان $$t$$ به دست آوریم.

$$\large \frac{ d N }{ N } = - \lambda d t$$
(2)

$$\large \Rightarrow \int_{ N_{ 0 } }^{ N } \frac{ d N }{ N } = - \lambda \int_{ t_{ 0 } }^{ t } d t$$
(3)

در رابطه (۳)، $$N_{0}$$ تعداد رادیونوکلیدهای اولیه در زمان اختیاری $$t_{0}$$ است. جهت سادگی کار اگر $$t_{0}$$ را برابر با صفر فرض کنیم، نتیجه نهایی رابطه (۳) به شکل زیر در می‌آید:

$$\large ln \frac{ N }{ N_{0} } = - \lambda t$$
(4)

با استفاده از تعریف لگاریتم طبیعی داریم:

$$\large \frac{ N }{ N_{0} } = e^{ - \lambda t }$$
(5)

$$\large \Rightarrow N = N_{0} e^{ - \lambda t }$$
(6)

رابطه فوق، به رابطه واپاشی پرتوزا نیز موسوم بوده که با مدل ریاضی آن در مقاله «نیمه عمر — به زبان ساده» آشنا شدیم. در فیزیک هسته‌ای، رابطه (6) را اغلب به صورت آهنگ واپاشی $$R$$ که معادل با $$R \equiv - \frac{ d N }{ d t }$$ است بیان می‌کنند. جهت بیان واپاشی پرتوزا برحسب $$R$$ از دو سمت رابطه (6) مشتق زمانی می‌گیریم.

$$\large \Rightarrow \frac{ \text{d} }{ \text{d} t } \rightarrow N = N_{0} e^{ - \lambda t } \Rightarrow R = - \frac{ \text{d} N }{\text{d} t } = \lambda N_{0} e^{ \lambda t }$$
(7)

در رابطه فوق، $$R_{0}$$ آهنگ واپاشی در زمان $$t = 0$$ و $$R$$ آهنگ واپاشی در زمان‌های بعدی $$t$$ است. بر اساس دو رابطه (6) و (7) رابطه زیر نتیجه می‌شود.

$$\large R = \lambda N$$
(8)

دقت داشته باشید که آهنگ واپاشی $$R$$ و $$N$$ (تعداد رادیواکتیوهایی که هنوز دچار واپاشی پرتوزا نشده‌اند) باید در یک لحظه محاسبه شوند.

در مباحث فیزیک هسته‌ای، آهنگ واپاشی $$R$$ کل یک نمونه پرتوزا (شامل یک یا چند رادیونوکلید) به فعالیت نمونه (activity of sample) موسوم است. واحد سنجش فعالیت در سیستم بین‌المللی $$SI$$ بکرل (becquerel) با نماد $$Bq$$ است. لازم به ذکر است که این واحد به افتخار هانری بکرل (Henri Becquerel) کاشف پدیده پرتوزایی انتخاب شده است. هر یک بکرل، به معنی یک واپاشی پرتوزا در ثانیه است.

$$1\ becquerel\ =\ 1\ Bq\ =\ 1\ decay\ per\ second$$
(9)

یکی دیگر از واحدهای سنجش فعالیت، کوری (curie) با نماد $$Ci$$ است. با این که این واحد قدیمی است، اما برخی مراجع همچنان از آن استفاده می‌کنند. رابطه بین کوری ($$Ci$$) و بکرل ($$Bq$$) به صورت زیر است.

$$1\ cirie\ =\ 1\ Ci\ =\ 3.7 \times 10^{10}\ Bq$$
(10)

واپاشی‌های پرتوزا در یک نگاه

در شکل زیر، واپاشی‌های پرتوزا خلاصه شده‌اند. مهم‌ترین واپاشی پرتوزا مربوط به ۳ واپاشی آلفازا (α)، بتازا (β) و گامازا (γ) است که کاربردهای بسیار زیادی در شاخه‌های مختلف فیزیک هسته‌ای دارند. لازم به ذکر است که در فیزیک هسته‌ای و علوم مهندسی مرتبط، به هسته‌ یا نوکلید اولیه که هنوز دچار واپاشی نشده است، هسته مادر یا والد و به هسته یا نوکلیدی که پس از فرآیند واپاشی باقی می‌ماند، هسته دختر می‌گویند.

جهت مشاهده تصویر در سایز اصلی، روی آن کلیک کنید.

طول عمر (Lifetimes)

جهت سنجش یا اندازه‌گیری عمر رادیونوکلیدهای یک نمونه هسته‌ای، غالباً دو معیار متداول نیمه عمر (half life) و عمر میانگین/متوسط (mean\average life) را به کار می‌برند.

نیمه عمر را با نماد $$\large T_{ 1 / 2}$$ نشان‌ داده و بیانگر مدت زمانی است که دو کمیت $$N$$ یا $$R$$ به نصف مقدار اولیه خود می‌رسند. عمر میانگین نیز که آن را با نماد $$\large \tau$$ نشان می‌دهند، بیانگر مدت زمانی است که دو کمیت $$N$$ و $$R$$ به $$\large \frac{ 1 }{ e }$$ مقدار اولیه خود برسند. رابطه معیار نیمه عمر به صورت زیر است:

$$\large \frac{ 1 }{ 2 } R_{0} = R_{0} e^{ \lambda T_{ 1 / 2 } }$$
(11)

فیلم آموزش فیزیک مدرن با رویکرد حل مساله در فرادرس

کلیک کنید

همچنین رابطه بین $$\large T_{ 1 / 2}$$ و $$\large \tau$$ با ثابت فروپاشی λ به صورت زیر است. پیشنهاد می‌کنیم جهت آشنایی با روند به دست آوردن رابطه (11)، به مقاله «نیمه عمر -- به زبان ساده» مراجعه فرمایید.

$$\large T_{ 1 / 2 } = \frac{ ln2 }{ \lambda } = \tau ln2$$
(12)

مثال: موز رادیواکتیو

در یک میوه موز بزرگ، در حدود ۶۰۰ میلی‌گرم پتاسیوم (Potassium) پرتوزای $$^{40} K$$ با درصد فراوانی $$0.0117$$ وجود دارد. اگر نیمه عمر پتاسیوم $$^{40} K$$ در حدود $$1.25 \times 10^{9}\ years$$ باشد، فعالیت هسته‌ای (آهنگ واپاشی پرتوزا $$R$$) موز به چه صورت است؟

مطابق با رابطه (۸) دیدیم که رابطه بین $$R$$ و $$N$$ به صورت زیر است.

$$\large R = \lambda N$$
(13)

در اینجا $$N_{40}$$ تعداد نوکئون‌های هسته اتم $$^{40} K$$ در موز است (بدیهی است که تعداد اتم‌ها نیز همین مقدار است). با استفاده از رابطه (12) می‌توانیم رابطه (13) را به صورت زیر بنویسیم.

$$\large R = \frac{ N_{40} l n 2 }{ T_{ 1 / 2 } }$$
(14)

مطابق با صورت مسئله، فراوانی تعداد رادیونوکلیدهای $$^{40} K$$ برابر با $$0.0117$$ است. به عبارت دیگر، 0.0117 درصد کل اتم‌های پتاسیوم در موز از نوع $$^{40} K$$ است. در اینجا نیاز داریم تا تعداد $$N_{40}$$ پتاسیوم در موز را بدست آوریم.

از مباحث مقدماتی شیمی می‌دانیم که رابطه به دست آوردن مول به شکل $$\large n = \frac{ N }{ N_{A} }$$ است. $$N_{A}$$ عدد آووگادرو با مقدار $$6.02 \times 10^{ 23 }\ mol^{ - 1 }$$ است. رابطه دیگری که برای محاسبه مقدار مول می‌توانیم از آن استفاده کنیم، رابطه $$n = \frac{ M_{sam} }{ M }$$ است که در آن $$M_{sam}$$ جرم نمونه و $$M$$ جرم مولی است. با مساوی قرار دادن این دو رابطه، $$n$$ را حذف کرده و می‌توانیم مقدار $$N_{40}$$ را به دست آوریم. در اینجا $$M_{sam}$$ برابر با 600 میلی‌گرم است.

$$\large N_{ 40 } = ( 1.17 \times 10^{ - 4 } ) \frac{ M_{sam} N_{A} }{ M }$$
(15)

از جدول‌های اطلاعاتی عناصر، جرم مولی پتاسیوم برابر با $$M_{K} = 39.102\ g/mol$$ است. در نتیجه داریم:

$$\large N_{ 40 } = ( 1.17 \times 10^{ - 4 } ) \frac{ ( 600 \times 10^{ - 3 }\ g ) ( 6.02 \times 10^{ 2 3 }\ m o l^{ - 1 } ) }{ 3 9 . 1 0 2\ g / mol } = 1.081 \times 10^{ 1 8 }$$
(16)

با توجه به مقدار $$N_{40}$$، از رابطه (14) نتیجه می‌شود:

$$\large R = \frac{ N_{40} l n 2 }{ T_{ 1 / 2 } } = \frac{ ( 1.081 \times 10^{18} ) ( l n 2 ) }{ ( 1.25 \times 10^{ 9 }\ y ) ( 3.16 \times 10^{ 7 }\ s/y ) } = 18.96\ Bq \approx 19.0\ Bq \approx 0.51\ nCi$$
(17)

این مقدار بسیار ناچیز بوده و خطری برای بدن ما ندارد. بر اساس اطلاعات پزشکی، خوردن موز، کمتر از یک درصد به تابش دریافتی بدن از پتاسیوم رادیواکتیو $$^{40} K$$ اضافه می‌کند.

محاسبه نیمه عمر و ثابت فروپاشی از روی نمودار

به عنوان مثال، برخی از اندازه‌گیری‌های فعالیت هسته‌ای (آهنگ واپاشی $$R$$) برای رادیونوکلید $$^{128} I$$ در جدول زیر نشان داده است. رادیونوکلید $$^{128} I$$ اغلب در فیزیک پزشکی به عنوان ردیاب در داخل بدن بیماران به کار گرفته شده و به وسیله آن، میزان جذب ید (iodine) توسط غده تیروئید (thyroid gland) را بررسی می‌کنند.

با توجه به داده‌های جدول فوق، می‌توان نمودار خطی ساده زیر را رسم کرد. در این نمودار لگاریتم طبیعی فعالیت هسته‌ای یا همان آهنگ واپاشی $$R$$ بر حسب زمان رسم شده است.

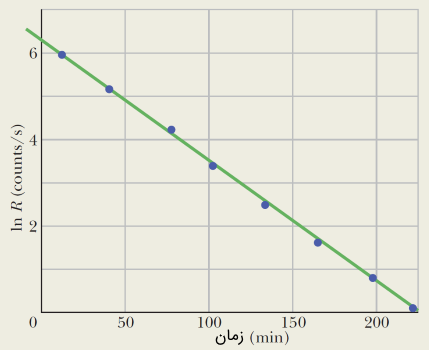
علت اینکه محور قائم، برحسب لگاریتم طبیعی $$R$$ رسم شده است، به راحتی از معادله (7) قابل تشخیص است. همان‌طور که دیدیم، آهنگ واپاشی $$R$$ به صورت رابطه زیر بیان می‌شود:

$$\large R = R_{0} e^{ \lambda t }$$
(18)

جهت حذف عدد نپر ($$e$$) از دو سمت رابطه فوق، لگاریتم طبیعی می‌گیریم. در نتیجه:

$$\large l n \rightarrow R = R_{0} e^{ \lambda t } \Rightarrow l n ( R ) = l n ( R_{0} e^{ \lambda t } ) = l n ( R_{0} ) + l n ( e^{ \lambda t } ) = l n ( R_{0} ) - \lambda t$$
(19)

همان‌طور که ملاحظه می‌فرمایید، رابطه فوق به فرم معاله خط $$y = m x + b$$ است. با توجه به رابطه (19) و معادله استاندارد خط، در اینجا $$l n R \equiv y$$ و $$t \equiv x$$ است. همچنین شیب‌خط $$m$$ برابر با ثابت واپاشی λ است.

حال با توجه به داده‌های جدول مذکور و تعیین نقطه‌ها، می‌توانیم نمودار شکل (6) را نتیجه بگیریم. همان‌طور که بیان کردیم، شیب خط معادل با ثابت فروپاشی λ است. در نتیجه با محاسبه شیب خط ($$m = \frac{ \triangle y }{ \triangle x }$$) به صورت زیر، ثابت فروپاشی λ حاصل می‌شود (تقریبی).

$$\large m \equiv \lambda = \frac{ 0 - 6.2 }{ 225\ min - 0 } = | 0.0276\ min^{ - 1 }|$$
(20)

توجه داشته باشید که شیب نمودار منفی است. حال با توجه به رابطه (12)، به راحتی می‌توانیم نیمه عمر را به دست آوریم.

$$\large T_{ 1 / 2 } = \frac{ l n 2 }{ \lambda } = \frac{ l n 2 }{ 0.0276\ min^{ - 1 } } \approx 25\ min$$
(21)

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های فیزیک
• آموزش فیزیک مدرن با رویکرد حل مساله
• مجموعه آموزش‌های شیمی
• آموزش نظریه اتم ها در مولکول ها با نرم افزار محاسباتی AIM2000
• پله پتانسیل (Potential Step) — به زبان ساده
• طیف الکترومغناطیسی -- به زبان ساده
• میزر (Maser) -- به زبان ساده