نوع داده عددی در پایتون – به زبان ساده
در «زبان برنامهنویسی پایتون» (Python Programming Language)، شش «نوع داده» (Data Type) اصلی وجود دارد. این انواع داده، شامل «عدد» (Number)، «لیست» (List)، «تاپل» (Tuple)، «رشته» (String)، «مجموعه» (Set) و «دیکشنری» (Dictionary) میشوند. نوع داده عددی در پایتون خود انواع مختلفی دارد. آگاهی از این انواع داده نه تنها برای برنامهنویسی در این زبان لازم است، بلکه گاهی نیاز میشود برخی از انواع دادههای عددی موجود را برای حل یک مساله، به نوع داده عددی دیگری تبدیل کرد. در این مطلب، انواع دادههای عددی در پایتون آموزش داده میشوند. سپس، به چگونگی تبدیل یک نوع داده به دیگری پرداخته میشود. در نهایت، عملیات ریاضی قابل انجام روی انواع داده عددی در پایتون مورد بررسی قرار میگیرد.


نوع داده عددی در پایتون
پایتون از نوع دادههای «اعداد صحیح» (integers)، «اعداد ممیز شناور» (floating point) و «اعداد مختلط» (complex numbers) پشتیبانی میکند. این انواع داده، به ترتیب به صورت کلاس float ،complex و int در پایتون تعریف میشوند. اعداد صحیح و ممیزشناور با وجود یا عدم وجود علامت ممیز اعشاری از یکدیگر متمایز میشوند. در واقع، در صورتی که در عدد از ممیز اعشاری استفاده شده باشد، آن عدد ممیز شناور و در غیر این صورت صحیح است.
برای مثال، ۵ یک عدد صحیح و ۵.۰ یک عدد ممیز شناور است. اعداد مختلط به صورت x + yj نوشته میشوند که در آن، x قسمت حقیقی و y قسمت موهومی عدد است. میتوان از تابع Type در پایتون برای فهمیدن اینکه یک متغیر به کدام کلاس تعلق دارد استفاده کرد. همچنین، از ()isinstance میتوان به منظور فهمیدن اینکه آیا یک متغیر به یک کلاس خاص تعلق دارد یا خیر استفاده کرد. برای درک بهتر این موضوع، مثال زیر قابل توجه است.
در کد بالا، مقدار 5 به متغیر a تخصیص داده شده است. سپس، با استفاده از تابع ()type نوع این متغیر مورد بررسی قرار گرفته است. خروجی این قسمت از کد، int خواهد بود. سپس، با استفاده از دستور (type(5.0 نوع داده عدد ۵.۰ بررسی و با استفاده از تابع ()print چاپ شده است. این خروجی برابر با نوع Float در پایتون خواهد بود. در نهایت، متغیر c به صورت c = 5 + 3j تعریف شده است که یک عدد مختلط به شمار میآید. سپس، با استفاده از دستور (isinstance(c, complex بررسی شده که آیا متغیر c متعلق به کلاس مختلط است و خروجی آن، با استفاده از دستور ()print چاپ شده است. در واقع تابع ()isinstance در تابع ()print قرار گرفته که موجب میشود خروجی آن با استفاده از تابع پرینت چاپ شود.
نوع داده صحیح (int) میتواند هر طولی داشته باشند؛ اما نوع داده ممیز شناور تنها تا ۱۵ رقم اعشار صحیح است (رقم ۱۶ نادرست است). اعدادی که افراد به صورت روزانه با آنها سر و کار دارند، اعداد دهدهی (در مبنای ۱۰ | Decimal) هستند. اما برنامهنویسهای کامپیوتری (معمولا برنامهنویسهای سیستمهای توکار) نیاز به کار با اعداد دودویی (مبنای ۲ | Binary)، شانزدهشانزدهی (مبنای ۱۶| Hexadecimal) و هشتهشتی (مبنای ۸| Octal) دارند. در پایتون، این اعداد با قرار دادن یک پیشوند پیش از آن عدد، مشخص میشوند. در تصویر زیر، این پیشوندها موجود هستند.
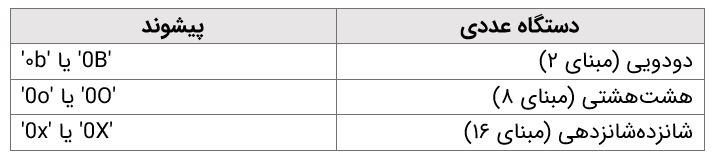
در ادامه، مثالهایی در همین رابطه آورده شده است.
خروجی حاصل از اجرای قطعه کد بالا، به صورت زیر خواهد بود.
همانطور که مشهود است، با قرار دادن 0b پیش از عدد دودویی 1101011 (به صورت 0b1101011) و پرینت کردن آن، در خروجی مقدار دهدهی ۱۰۷ چاپ شده است. در خط کد بعدی، عدد دودویی 0b10 (برابر با ۲ در دستگاه مبنای ۱۰) با عدد مبنای شانزده 0xFB (برابر با ۲۵۱ در دستگاه مبنای ۱۰) جمع زده شده و خروجی آن با استفاده از تابع ()print چاپ شده که برابر با مقدار ۲۵۳ است. در آخرین خط کد، مقدار 0o15 که در مبنای هشت است، به تابع ()print داده شده و خروجی حاصل از آن، برابر با ۱۳ (عدد ۱۳ در مبنای ۱۰) است.
تبدیل انواع
میتوان یک نوع داده را به نوع دیگری تبدیل کرد. این کار عناوین گوناگونی، شامل type coercion ،type casting ،type conversion و type juggling دارد. کلیه این عبارات، به مفهوم «تبدیل نوع» در پایتون اشاره دارند. در صورت انجام دادن عملیاتی مانند جمع و تفریق بین اعداد صحیح و اعشاری، به طور ضمنی تبدیل نوع برای اعداد صحیح انجام میشود.
در واقع، امکان جمع زدن یا تفریق یک عدد صحیح با یک عدد ممیز شناور وجود ندارد؛ بنابراین، در صورت انجام چنین کاری، عدد صحیح ابتدا به ممیز شناور تبدیل میشود و سپس عمل جمع یا تفریق انجام میشوند. شایان ذکر است که خروجی نیز به صورت عدد اعشاری خواهد بود. مثال زیر در همین رابطه، جالب توجه است.
در قطعه کد بالا، ۱ عدد صحیحی است که با عدد ممیز شناور ۲.۰ جمع زده شده است. بنابراین، ۱ ابتدا به ۱.۰ (ممیز شناور) تبدیل و سپس با ۲.۰ جمع زده شده است. خروجی نیز ۳.۰ است که یک عدد ممیز شناور محسوب میشود. همچنین، میتوان از توابع توکاری مانند ()float() ،int و ()complex برای تبدیل صریح انواع به یکدیگر استفاده کرد. این توابع، میتوانند «رشتهها» (Strings) را نیز تبدیل کنند.
در قطعه کد بالا، عدد ممیز شناور ۲.۳ به تابع ()int داده شده است. خروجی حاصل از اجرای کد برابر با ۲ (عدد صحیح) است. در خط کد بعدی، عدد ۲.۸- به تابع ()int داده شده و خروجی آن، عدد صحیح ۲- است. عدد صحیح ۵، با استفاده از تابع ()float به عدد ممیز شناور ۵.۰ تبدیل شده است. در نهایت، رشته '3+5j'، با استفاده از تابع ()complex، به عدد مختلط تبدیل شده است. نکته مهم در تبدیل اعداد ممیز شناور به اعداد صحیح، آن است که بخش اعشاری عدد بریده (Truncated) میشود.
ممیز شناور پایتون
کلاس «شناور» (float) توکار پایتون، محاسبات فوقالعادهای ار انجام میدهد که بسیاری از افراد از مشاهده آن شگفتزده میشوند. چنانچه واضح است، مجموع ۱.۱ و ۲.۲ برابر با ۳.۳ است. اما به نظر میرسد پایتون با این موضوع مخالف است. قطعه کد زیر، این مساله را نشان میدهد.
False
سوالی که در این وهله مطرح میشود آن است که دلیل این امر چیست؟ وقوع این مساله از آنجا نشات میگیرد که مقادیر ممیز شناور در سختافزار کامپیوتری به صورت کسرهای دودویی ذخیره میشوند؛ زیرا کامپیوترها فقط مقادیر (۰ و ۱) را میفهمند. به همین دلیل، اغلب کسرهای اعشاری شناخته شده برای انسان، به درستی و عینا در کامپیوتر ذخیره نمیشوند. در ادامه، مثال دیگری در همین رابطه ارائه شده است. کسر ۱/۳ را نمیتوان به صورت یک عدد اعشاری نشان داد.
زیرا مقدار آن برابر با ۰.۳۳۳۳۳۳۳... با دوره تناوب روی ۳ است و بنابراین قسمت اعشاری به صورت نامحدودی ادامه خواهد داشت. این عدد را تنها میتوان تقریب زد. برای کسر اعشاری ۰.۱ نیز به همین صورت است و کسر ...0.000110011001100110011 برای آن حاصل میشود. این در حالی است که کامپیوتر، تنها مقدار محدودی از آن را ذخیره میکند. همین امر موجب میشود که ۰.۱ فقط تخمین زده شود و دقیقا برابر با عدد اصلی نباشد. از این رو، مواجه شدن با پیامی مانند آنچه در قطعه کد بالا وجود داشت، مربوط به محدودیت کامپیوتر است، نه خطای پایتون.
3.3000000000000003
برای غلبه بر چنین مسائلی، میتوان از ماژول decimal که در پایتون وجود دارد استفاده کرد. در حالی که مقادیر ممیز شناور دارای دقتی تا ۱۵ رقم اعشار هستند، ماژول اعشاری دارای دقت قابل تنظیم به وسیله کاربر است. قطعه کد زیر، مثالی در همین رابطه را ارائه میکند.
در قطعه کد بالا، ماژول decimal «وارد» (Import) شده است. سپس، عدد ممیز شناور ۰.۱ با استفاده از تابع ()print چاپ شده است. خروجی حاصل از اجرای این بخش از کد، برابر با ۰.۱ است. سپس، با استفاده از ماژول decimal، عدد ۱.۰ با دقت بیشتری چاپ شده است. خروجی برابر با 0.1000000000000000055511151231257827021181583404541015625 است. این ماژول هنگامی مورد استفاده قرار میگیرد که هدف انجام محاسباتی مانند آنچه در دوران مدرسه وجود داشت، باشد. همچنین، معنیدار بودن را نیز حفظ میکند. واضح است که عدد ۲۵.۵۰ کیلوگرم، از ۲۵.۵ دقیقتر است، زیرا نسبت به حالت دوم دارای یک رقم اعشار معنیدار بیشتر است. کد زیر در همین رابطه مورد توجه است.
ابتدا، از ماژول decimal تابع Decimal با عنوان D فراخوانی میشود. سپس، اعداد ممیز شناور ۱.۱ و ۲.۲ در حالی که هر یک به تابع D داده شدهاند، با یکدیگر جمع زده میشوند و حاصل جمع با استفاده از دستور print چاپ میشود. خروجی برابر با ۳.۳ است. در خط کد بعدی، اعداد ممیز شناور ۱.۱ و ۲.۲ در حالی که به تابع D داده شدهاند در یکدیگر ضرب میشوند. حاصل این ضرب برابر با 3.۰۰۰ است. دنباله صفرها در خروجی قابل توجه است. ممکن است این پرسش مطرح شود که چرا هر بار از Decimal به جای float در پیادهسازیها استفاده نشود؟ دلیل اصلی این امر افزایش کارایی است. عملیات ممیز شناور سریعتر از عملیات Decimal انجام میشود.
چه زمانی از Decimal استفاده شود؟
معمولا، از Decimal در شرایط زیر استفاده میشود:
- هنگام ساخت برنامههای کاربردی مالی که نیاز به ارائه اعشاری دقیق دارند.
- هنگامی که نیاز به کنترل سطح دقت (صحت) وجود دارد.
- هنگامی که قصد پیادهسازی مفهوم ارقام اعشاری معنیدار وجود دارد.
- هنگامی که نیاز به انجام عملیاتی مانند آنچه در مسائل مدرسه وجود داشت، باشد.
کسرهای پایتون
پایتون، عملیاتی شامل اعداد کسری از طریق ماژول fractions را فراهم میکند. یک کسر، دارای صورت و مخرج است. هر دو این مقادیر اعداد صحیح هستند. این ماژول از محاسبات اعداد گویا نیز پشتیبانی میکند.
«اشیا» (objects) کسر را میتوان به روشهای مختلف ساخت.
در قطعه کد بالا، عدد اعشاری ۱.۵ به تابع Fraction از ماژول fractions داده شده است. سپس، خروجی حاصل از تابع با استفاده از تابع print چاپ میشود که برابر با کسر ۳/۲ است. در خط کد بعدی که مثال دیگری برای همین تابع است، مقدار ۵ به تابع داده شده که خروجی آن نیز برابر با ۵ است (در واقع کسر ۵/۱ است که در آن معمولا فقط صورت نوشته میشود).
در نهایت، مقادیر ۱ و ۳ به ترتیب به تابع داده شدهاند (به صورت (fractions.Fraction(1,3) که خروجی تابع برای این مورد کسر ۱/۳ است. هنگام ساخت Fraction از float، ممکن است نتایج غیرمعمولی حاصل شود. این مساله به دلیل نمایش نامناسب اعداد ممیز شناور دودویی است که پیشتر درباره آن صحبت شد. خوشبختانه، Fraction این امکان را فراهم میکند تا از رشتهها نیز کسر ساخت. این گزینه هنگام کار با مقادیر decimal کاربردی خواهد بود.
در قطعه کد بالا، پس از وارد کردن ماژول fractions، مقدار ۱.۱ به تابع Fraction داده شده و خروجی آن با استفاده از تابع ()print چاپ میشود. این مقدار برابر با 2476979795053773/2251799813685248 است. در خط کد بعدی، رشته '1.1' به تابع داده میشود که خروجی آن برابر با 11/10 است. این نوع داده از همه عملیات ریاضیاتی پایه پشتیبانی میکند. در ادامه، مثالهایی در همین رابطه ارائه شده است.
در قطعه کد بالا، ابتدا تابع Fraction از ماژول fractions با عنوان F، وارد میشود. سپس، مقادیر ۱ و ۳ به ترتیب به تابع F داده میشوند و حاصل دو تابع (F(1,3 با هم جمع زده میشود. از آنجا که برای هر تابع (F(1,3، خروجی برابر با ۱/۳ است، حاصل جمع برابر با ۲/۳ میشود. در خط کد بعدی، مقدار ۱ تقسیم بر (F(5,6 محاسبه میشود.
در واقع، حاصل تقسیم کسری ۱/۱ بر ۵/۶ محاسبه میشود که برابر با ۶/۵ است. در (print(F(-3,10) > 0، بررسی میشود که آیا خروجی تابع (F(-3,10 بزرگتر از صفر است یا خیر. به دلیل آنکه خروجی (۳/۱۰-) از صفر بزرگتر نیست، False چاپ میشود. در نهایت، در خط کد آخر بررسی میشود که آیا خروجی تابع (F(-3,10 کوچکتر از صفر است یا خیر. به دلیل آنکه خروجی، یعنی ۳/۱۰- از صفر کوچکتر است، True در خروجی چاپ میشود.
ریاضیات پایتون
ماژولهایی مانند ماژول math و ماژول random در پایتون، برای مباحث گوناگون ریاضی مانند مثلثات، لگاریتم، آمار و احتمال ارائه شدهاند.
در قطعه کد زیر، مثالهایی از این موارد آورده شده است.
مثالهایی از محاسبات ریاضی قابل انجام به وسیله تابع random در ادامه آمده است.
اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای برنامهنویسی پایتون Python
- آموزش تکمیلی برنامهنویسی پایتون
- مجموعه آموزشهای دادهکاوی و یادگیری ماشین
- زبان برنامهنویسی پایتون (Python) — از صفر تا صد
- یادگیری علم داده (Data Science) با پایتون — از صفر تا صد
- افزایش فالوورهای اینستاگرام با ربات پایتون — راهنمای کاربردی
- آموزش پایتون (Python) — مجموعه مقالات جامع وبلاگ فرادرس
- کاربرد پایتون چیست و با آن چه میتوان کرد؟ | راهنمای کاربردی
- متد Split در پایتون – توضیح به زبان ساده با مثال و کد
^^












سلام
وقتی عمل تقسیم انجام میدم بصورت عدد صحیح نشان میدهد.مشکل از کجاست؟
باپایتون برنامه ای بنویسیدباتعریف توابع سه عددراگرفته بزرگترین رانشان دهد
ممنون خانوم حصاری که اینقدر با حوصله و خوب توضیح دادید……واقعا عالی بود