نمودار گذر سیگنال — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

در آموزش‌های پیشین مجله فرادرس، درباره نمودار بلوکی سیستم‌ها و نحوه ساده‌سازی آن‌ها برای به‌دست آوردن تابع تبدیل بحث کردیم. اگر تعداد بلوک‌های سیستم زیاد باشد، ساده‌سازی نمودار بلوکی کاری دشوار است. یکی دیگر از ابزارهای مفید برای نمایش تصویری سیستم‌ها، نمودار گذر سیگنال است که به‌جای ساده‌سازی، با استفاده از یک فرمول می‌توان تابع تبدیل سیستم مرتبط با آن را به‌دست آورد. در این آموزش، اجزای اصلی نمودار گذر سیگنال و روش رسم آن را توضیح خواهیم داد.

اجزای اصلی نمودار گذر سیگنال

گره و شاخه، اجزای اصلی یک «نمودار گذر سیگنال» (Signal-flow Graph) هستند.

فیلم آموزش کنترل خطی با رویکرد حل مساله در فرادرس

کلیک کنید

گره

«گره» (Node) نقطه‌ای است که یک متغیر یا یک سیگنال را نمایش می‌دهد. سه نوع گره مختلف وجود دارد:

• گره ورودی: گره‌ای است که فقط یک شاخه خروجی دارد.
• گره خروجی: گره‌ای است که فقط یک شاخه ورودی دارد.
• گره ترکیبی: گره‌ای است که شاخه‌ها، هم به آن وارد و هم از آن خارج می‌شوند.

مثال

نمودار گذر سیگنال شکل زیر را در نظر بگیرید.

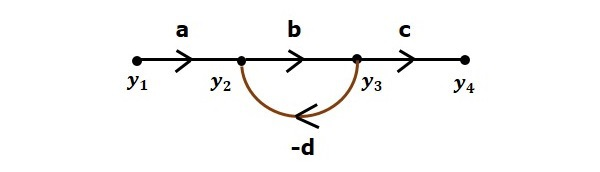
• گره‌های نمودار گذر سیگنال شکل بالا $$y_1$$، $$y_2$$، $$y_3$$ و $$y_4$$ است.
• $$y_1$$ و $$y_۴$$ به‌ترتیب، گره‌های ورودی و خروجی هستند.
• $$y_2$$ و $$y_3$$ گره‌های ترکیبی هستند.

شاخه

«شاخه» (Branch)، پاره‌خطی است که دو گره را به یکدیگر ارتباط می‌دهد و هم بهره دارد هم جهت. برای مثال، نمودار گذر سیگنال شکل بالا،‌ چهار شاخه دارد. بهره این شاخه‌ها c ،b ،a و d- است.

رسم نمودار گذر سیگنال

فرض کنید می‌خواهیم نمودار گذر سیگنال معادلات جبری زیر را رسم کنیم:

$$\large y _ 2 = a _ { 1 2 }  y _ 1 + a _ { 4  2 } y _ 4$$

$$\large y _ 3 = a _ { 2 3 } y _ 2 + a _ { 5 3 } y _ 5$$

$$\large y _ 4 = a _ { 3 4 } y _ 3$$

$$\large y _ 5 = a _ { 4 5 }  y _ 4 + a _ { 3 5 } y _ 3$$

$$\large y _ 6 = a _  { 5 6 } y _ 5$$

فیلم آموزش سیستم های کنترل خطی در فرادرس

کلیک کنید

نمودار گذر سیگنال مربوط به معادلات بالا، شش گره ($$y_1$$، $$y_2$$، $$y_3$$، $$y_4$$ $$y_5$$ و $$y_6$$) و هشت شاخه دارد. بهره این شاخه‌ها $$a_{12}$$، $$a_{23}$$، $$a_{34}$$، $$a_{45}$$، $$a_{56}$$، $$a_{42}$$، $$a_{53}$$ و $$a_{35}$$ است.

برای رسیدن به نمودار گذر سیگنال کامل، نمودار گذر سیگنال هریک از معادله‌ها را به‌صورت جداگانه رسم، سپس آن‌ها را با هم ترکیب می‌کنیم.

مرحله ۱. رسم نمودار گذر سیگنال $$y_2 = a_{13}y_1 + a_{42}y_4$$:

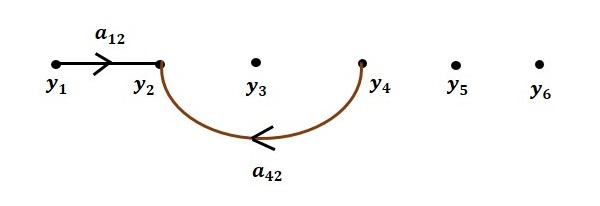
مرحله ۲. رسم نمودار گذر سیگنال $$y_3 = a_{23}y_2 + a_{53}y_5$$:

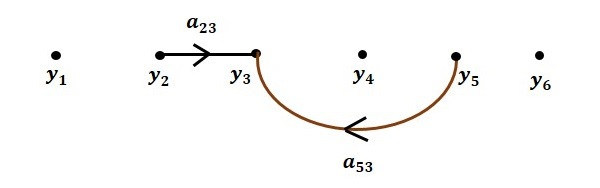
مرحله ۳. رسم نمودار گذر سیگنال $$y_4 = a_{34}y_3$$:

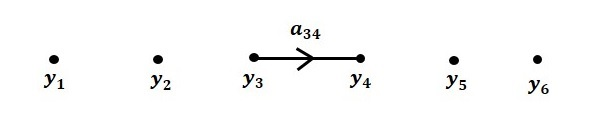
مرحله ۴. رسم نمودار گذر سیگنال $$y_5 = a_{45}y_4 + a_{35}y_3$$:

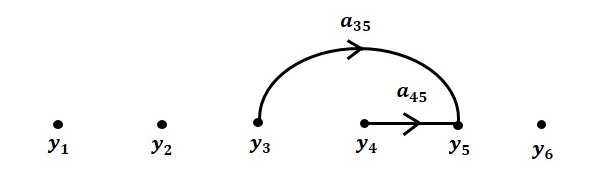
مرحله ۵. رسم نمودار گذر سیگنال $$y_6 = a_{56}y_5$$:

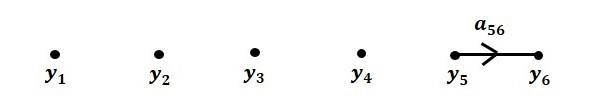
مرحله ۶. رسم نمودار گذر سیگنال کل سیستم:

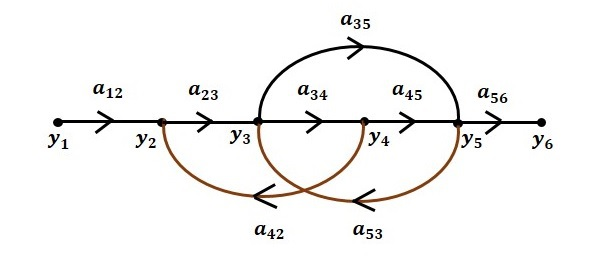
تبدیل نمودارهای بلوکی به نمودارهای گذر سیگنال

با انجام گام‌های زیر می‌توان یک نمودار بلوکی را به نمودار گذر سیگنال معادل آن تبدیل کرد:

• به‌جای هریک از سیگنال‌ها، متغیرها، نقاط جمع و نقاط انشعاب نمودار بلوکی، یک گره در نمودار گذر سیگنال قرار دهید.
• به‌جای هریک از بلوک‌های نمودار بلوکی، یک شاخه در نمودار گذر سیگنال قرار دهید.
• تابع تبدیل درون بلوک‌های نمودار بلوکی را به‌عنوان بهره شاخه‌های نمودار گذر سیگنال در نظر بگیرید.
• گره‌ها را با توجه به نمودار بلوکی به یکدیگر متصل کنید. اگر اتصالی بین دو گره وجود دارد (اما بلوکی بین آن‌ها نیست)، بهره شاخه را برابر با یک قرار دهید. برای مثال، بین نقاط جمع،‌ نقاط جمع و انشاب، ورودی و نقاط جمع، و نقاط انشعاب و خروجی شاخه‌ای با بهره یک قرار می‌گیرد.

مثال

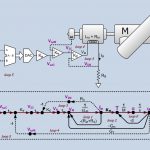
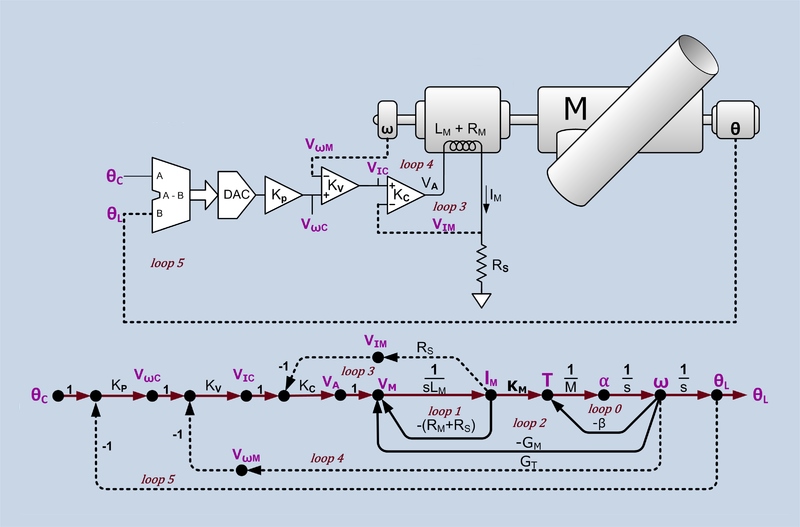
نمودار بلوکی شکل زیر را در نظر بگیرید. با توجه به نکاتی که گفته شد، می‌خواهیم نمودار گذر سیگنال معادل آن را رسم کنیم.

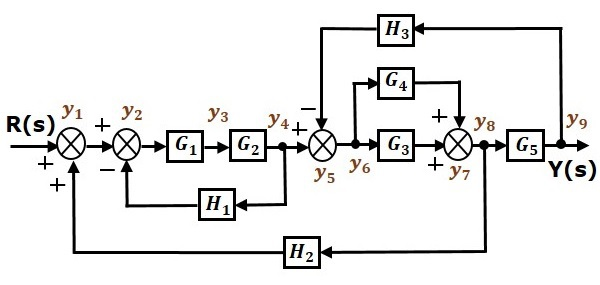
ورودی $$R(s)$$ و خروجی $$C(s)$$ نمودار بلوکی را به‌عنوان گره‌های ورودی و خروجی در نمودار گذر سیگنال قرار می‌دهیم. برای دقت بیشتر، سایر گره‌های نمودار بلوکی را $$y_1$$ تا $$y_9$$ نامگذاری می‌کنیم. از این نُه گره،‌ چهار گره مربوط به نقاط جمع، چهار گره مربوط به نقاط انشعاب و یک گره مربوط به متغیر بین بلوک‌های $$G_1$$ و $$G_2$$ است.

شکل زیر، نمودار گذر سیگنال معادل را نشان می‌دهد.

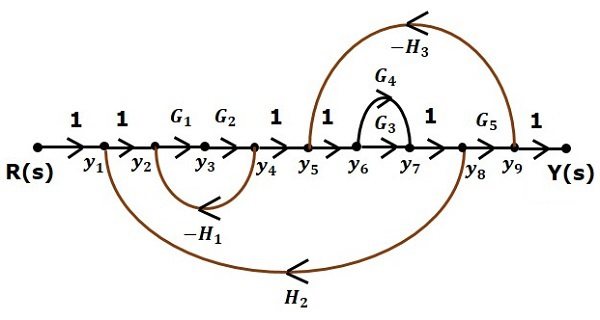
با استفاده از فرمول بهره میسون که در آموزش بعدی به آن خواهیم پرداخت، می‌توان تابع تبدیل نمودار گذر جریان را به‌دست آورد. محاسبه تابع تبدیل، بدون ساده‌سازی نمودار (برخلاف نمودار بلوکی) مزیت اصلی نمودار گذر سیگنال است.

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• نمایش سیستم های دینامیکی با متلب — از صفر تا صد
• سیستم کنترل حلقه باز — به زبان ساده
• مکان هندسی ریشه ها (Root Locus) در مهندسی کنترل — به زبان ساده

^^