نظریه قابلیت اعتماد — اصول و مفاهیم اولیه

یکی از کاربردهای اصلی آمار به منظور نمایش رفتار پدیده‌های تصادفی، در «نظریه قابلیت اعتماد» (Reliability Theory) نهفته است. از آنجایی که این نظریه بیشتر در مواردی مانند مهندسی و تعیین طول عمر دستگاه‌ها به کار گرفته می‌شود گاهی به آن «مهندسی قابلیت اعتماد» (Reliability Engineering) نیز می‌گویند. از این دیدگاه می‌توان قابلیت اعتماد را شاخه‌ای از «مهندسی سیستم‌ها» (System Engineering) دانست. با توجه به دیدگاه مهندسی می‌توان قابلیت اعتماد را توانایی در تعیین طول عمر یک سیستم براساس اجزای آن دانست. از این جهت می‌توان براساس تئوری احتمالات، میزان قابلیت اعتماد را احتمال عدم شکست (احتمال طول عمر) دانست و به صورت زیر نمایش داد.

$$ \large Reliability = 1- Probability\;of\;Failure$$

در این نوشتار به بررسی مفاهیم اولیه نظریه قابلیت اعتماد و کاربردهای آن خواهیم پرداخت. به منظور آشنایی بیشتر با مباحث به کار رفته در این نوشتار بهتر است مطلب قابلیت اعتماد (Reliability) برای سامانه‌های منسجم — به زبان ساده را مطالعه کنید. همچنین خواندن نوشتار داده‌ های سانسور شده (Censored Data) در آمار — به زبان ساده نیز خالی از لطف نیست.

نظریه قابلیت اعتماد

مفهوم و تعریف قابلیت اعتماد از دیدگاه مهندسی متفاوت ولی در یک راستا است. در ادامه فهرستی از تعاریف قابلیت اعتماد را ارائه کرده‌ایم.

• ایده‌ای که بیانگر قابلیت استفاده از یک دستگاه برای مدت مشخصی باشد.
• ظرفیت طراحی، تولید و نگهداری یک دستگاه به منظور انجام وظایف در یک مقطع زمانی.
• مقاومت در برابر خرابی یک دستگاه در طول زمان.
• احتمال آنکه یک دستگاه در یک بازه از زمان، فعال باشد.
• تعیین متوسط طول عمر یک دستگاه.
• تعیین زمان خرابی یک دستگاه.

همانطور که در تعریف بالا مشخص شده، نظریه قابلیت اعتماد، مرتبط با طول عمر دستگاه و زمان خرابی آن است.

فیلم آموزش مقدماتی نظریه قابلیت اعتماد در فرادرس

کلیک کنید

به این ترتیب اگر متغیر تصادفی $$T$$ را مرتبط با طول عمر یک دستگاه (یا یک مولفه از دستگاه) در نظر بگیریم، براساس نظریه احتمال، قابلیت اعتماد که آن را با $$R(t)$$ نشان می‌دهند، برای آن مطابق با رابطه زیر محاسبه خواهد شد.

$$ \large R(t)=Pr\{T>t\}=\int _{t}^{\infty }f(x)dx$$

مشخص است که در اینجا منظور از $$f(x)$$ تابع چگالی خرابی و $$t$$‌ نیز زمان است. این احتمال نشان می‌دهد که احتمال آنکه طول عمر دستگاه بیشتر از $$t$$ باشد چقدر است. در ادامه به مفاهیم اولیه در قابلیت اعتماد خواهیم پرداخت.

نکته: مفهوم طول عمر را برای افراد و بخصوص بیماران نیز می‌توان به کار برد. این موضوع مشخص می‌کند که مبحث نظریه قابلیت اعتماد در پزشکی و داروسازی بسیار مورد توجه است.

نرخ شکست و تحلیل بقا

«نرخ شکست» (Failure Rate) و «تحلیل بقا» (Survival Analysis)، بخش‌هایی از نظریه قابلیت اعتماد هستند که به طول عمر و نرخ خرابی یا شکست مولفه‌ها می‌پردازند. نرخ شکست، بیانگر فراوانی خرابی یک مولفه است که معمولا آن را با علامت $$\lambda$$ نشان می‌دهند. مشخص است که نرخ شکست متناسب با زمان تغییر می‌کند. برای مثال نرخ شکست (خرابی) یک خودرو در سال پنجم عمرش بسیار بیشتر از سال اول است. به این ترتیب احتمال آنکه قطعه‌ای مانند جعبه دنده، اگزوز و ... از خودرو خراب شود در سال پنجم بیشتر از سال اول است. البته می توان در نظر گرفت که در زمان یا دوره گارانتی ممکن است نرخ شکست صعودی باشد ولی در پایان دوره گارانتی، نرخ شکست نزولی بوده و در یک دوره که تقریبا متوسط عمر خودرو را شامل می‌شود، ثابت است. در انتهای دوره طول عمر خودرو، میزان اشکلات خودرو افزایش یافته و باعث کوتاه‌تر شدن طول عمر آن خواهد شد.

بطور معمول «متوسط زمان بین شکست» (Mean Time Between Failure) که به اختصار MTBF‌ نامیده می‌شود می‌تواند ملاکی برای طول زمان خرابی یک مولفه در نظر گرفته شود. معمولا بین MTBF و نرخ شکست رابطه زیر برقرار است.

$$\large MTBF =\dfrac{1}{\lambda}$$

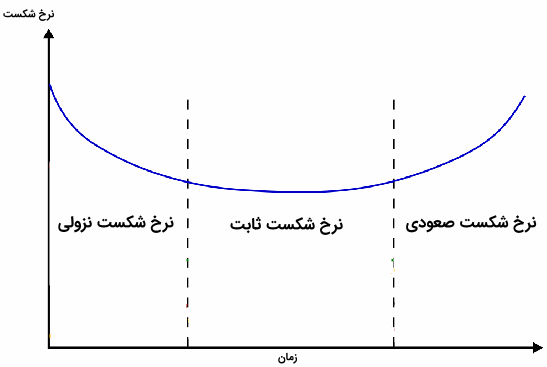
البته این تساوی در زمانی که نرخ شکست در طول زمان ثابت باشد، به کار می‌رود. ولی ممکن است نرخ شکست براساس زمان، به صورت یک «تابع صعودی» (Increasing Function)، «تابع نزولی» (Decreasing Function) یا «وانی شکل» (Bathtub Curve) باشد. در این میان سه مفهوم جدید برای نظریه قابلیت اعتماد ایجاد ‌می‌شود. اجزایی که نرخ شکست آن‌ها نزولی است با DFR یا Descreasing Failure Rate نشان داده می‌شوند. از طرفی اگر نرخ شکست برای یک مولفه به صورت صعودی باشد، نرخ شکست آن را AFR یا Ascending Failure Rate مورد خطاب قرار می‌دهند. البته ثابت بودن نرخ شکست نیز به شکل CFR یا Constant Failure Rate نشان داده می‌شود.

در این میان برای تحلیل بقا و تعیین توزیع احتمالی طول عمر هر مولفه یا سیستم، از توابع احتمال مختلفی ممکن است استفاده شود. البته باید توجه داشت که از آنجایی که طول عمر، شامل مقدارهای مثبت است، باید تکیه متغیر تصادفی و توزیع آن شامل مقدارهای مثبت (به همراه صفر) باشد. در این میان توزیع‌های زیر می‌توانند مفید به نظر آیند.

• توزیع نمایی (Exponential Distribution) می‌تواند قانون احتمال برای متغیر تصادفی مربوط به زمان رسیدن به اولین رخداد (موفقیت یا شکست) را نشان دهد. بنابراین در بیشتر موارد برای نشان دادن طول عمر بخصوص برای قطعات الکترونیکی از این توزیع استفاده می‌شود. خاصیت عدم حافظه یکی از خصوصیات جالب این توزیع است.
• توزیع یکنواخت (Uniform Distribution) از نوع پیوسته نیز یکی از مواردی است که در وبلاگ فرادس به آن پرداخته‌ایم. ارتباط این توزیع با دیگر توزیع‌های آماری در این نوشتار مورد بحث قرار گرفته است. همچنین تولید اعداد تصادفی از توزیع یکنواخت به کمک اکسل از مواردی است که در این مطلب وجود دارد. اگر بازه‌ای که برای تکیه‌گاه این متغیر تصادفی در نظر گرفته‌ایم شامل مقدارهای مثبت باشد، از این متغیر تصادفی برای تعیین طول عمر قطعات می‌توانیم استفاده کنیم.
• توزیع نرمال بریده شده (Truncated Normal Distribution)، به عنوان نوعی از توزیع نرمال است که از یک یا دو طرف محدود شده است. در مواردی که با داده‌های مثلا طول عمر مواجه هستیم از این توزیع می‌توان استفاده کرد. در نوشتاری از وبلاگ فرادرس به این توزیع پرداخته شده و شیوه شبیه‌سازی داده‌های با این توزیع مورد بررسی قرار گرفته است.
• توزیع لاگ نرمال (Log-normal Distribution)، نیز یکی دیگر از انواع توزیع‌های استخراج شده از توزیع نرمال است. اگر متغیر تصادفی $$X$$ دارای توزیع لاگ نرمال باشد، آنگاه توزیع $$Y=\ln(X)$$ نرمال است. در نتیجه تکیه‌گاه متغیر تصادفی $$X$$ مقدارهای مثبت بوده و می‌تواند به عنوان متغیر تصادفی بیان کننده طول عمر به کار رود.

سانسور داده‌ها در قابلیت اعتماد

یکی دیگر از مباحث مرتبط با نظریه  قابلیت اعتماد، داده‌های سانسور شده است. این امر زمانی اتفاق می‌افتد که هنگام اندازه‌گیری طول عمر نمونه تصادفی، بعضی از مولفه‌ها ممکن است از بین بروند (مثلا بر اثر بیماری یا سوختن یک قطعه) در نتیجه اندازه نمونه کاهش یافته و گاهی برآوردیابی به مشکل برخورد خواهد کرد.  در این میان باید از اطلاعاتی که درون داده‌های سانسور شده وجود داشته، حداکثر استفاده بشود.

فیلم آموزش تلفیق داده Data Fusion – مبانی و کاربردها در فرادرس

کلیک کنید

تکنیک‌هایی در تحلیل بقا و قابلیت اعتماد وجود دارد که براساس نوع سانسور انجام گرفته، دقت برآورد برای طول عمر را بیشتر می کنند. یا برعکس ممکن است که در طول دوره آزمایش هیچ خطا یا مشکلی گزارش نشود. در این صورت استفاده از سانسور داده‌ها امری ضروری تلقی می‌شود.

برای مثال ممکن است در طول یک روز راننده قطار هیچ خطایی نداشته باشد و یا دستگاه تولید منگنه در طول یک ساعت بدون تولید یک قطعه معیوب فعالیت کند. به این ترتیب نمی‌توان میزان خطای دستگاه تولید منگنه را برآورد کرد. در چنین مواردی استفاده از مدل‌های سانسور داده‌ها و یا داده‌های سانسور شده یک ابزار برای برآورد مناسب پارامترهای مدل و تعیین نرخ شکست است.

اگر مطلب بالا برای شما مفید بوده است، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار و احتمال
• آموزش مقدماتی نظریه قابلیت اعتماد
• آموزش آمار و احتمال مهندسی
• آزمایش تصادفی، پیشامد و تابع احتمال
• متغیر تصادفی و توزیع نمایی — به زبان ساده
• متغیر تصادفی و توزیع وایبل (Weibull Distribution) — به زبان ساده

^^