مدل سازی آرایه فتوولتاییک با هوش مصنوعی | پیاده سازی در متلب

توان خروجی یک نیروگاه معمولی را که برخلاف نیروگاه خورشیدی که به ماهیت منبع انرژی (خورشید) و سایر عوامل محیطی نظیر دمای محیط وابسته است، میتوان به سادگی کنترل کرد. مشکل اصلی سیستمهای فتوولتاییک، نامعینی توان خروجی آنهاست. بنابراین، برای استفاده مؤثر از این سیستمها، باید توان خروجی آنها را پیشبینی کرد. با پیشبینی دقیق توان خروجی سیستم میتوان بر ماهیت نامعین توان تولیدی غلبه کرد و در نتیجه قابلیت اطمینان کل سیستم را بهبود داد. مدلسازی یکی از راههای انجام این کار است. در این آموزش، با مدل سازی آرایه فتوولتاییک آشنا میشویم.
مدل سازی آرایه فتوولتاییک با شبکه عصبی
مدلهای مبتنی بر شبکه عصبی مصنوعی (ANN) راهکاری برای حل مشکل شرایط آب و هوایی متغیر هستند که رابطه غیرخطی بین متغیرهای ورودی و خروجی سیستم پیچیده را توصیف میکنند. توانایی خودیادگیری شبکههای عصبی، مزیت اصلی این مدلها محسوب میشود. بنابراین، این مدلها حین عملکرد نامعین، مانند توان خروجی آرایه سیستم، دقیق هستند.
شبکه عصبی مصنوعی، مجموعهای از تکنیکهای پردازش اطلاعات با الهام از رویکرد اطلاعات پردازش سیستم عصبی بیولوژیکی است. یک ANN از واحدهای جزئی موازی به نام نرون تشکیل شده است. نرونها به وسیله شمار زیادی از پیوندهای وزنی به هم وصل میشوند که امکان انتقال سیگنال یا اطلاعات را دارند. یک نرون، ورودیها را از طریق اتصالات ورودی خود دریافت و ورودیها و خروجیها را ترکیب میکند. مفهوم اصلی شبکههای عصبی ساختار سیستم پردازش اطلاعات، مشابه تکنیک تفکر انسان است. شبکه عصبی میتواند رابطه بین متغیرهای ورودی و خروجی را با مطالعه دادههای ثبت شده قبلی یاد بگیرد. مزیت اصلی ANN این است که با استفاده از آن میتوان برای مسائل پیچیده مربوط به فناوریهای معمول که راهحل الگوریتمی ندارند یا برای حل نیازمند یک الگوریتم پیچیدهتر هستند، راهحل مناسبی ارائه کرد.
برخی از شبکههای عصبی مختلف، عبارتند از: «شبکههای عصبی تابع پایه شعاعی» (Radial Basis Fnction Networks) یا RBF، «شبکههای پیوند تابعی» (Functional Link Networks)، «شبکههای عصبی رگرسیون عمومی» (General Regression Neural Networks) یا GRNN، «شبکههای کوهونن» (Kohonen Networks)، «شبکههای رو به جلوی آبشاری» (Cascade Forward Neural Network) یا CFNN، «شبکههای عصبی پیشخور» (Feedforward Neural Network) یا FFNN، «شبکههای گرام-شارلی» (Gram–Charlier Networks)، «کوانتیزاسیون بردار یادگیری» (Learning Vector Quantization)، «شبکههای هب» (Hebb Networks)، «شبکههای آدلاین» (Adaline Networks)، «شبکههای غیرمشارکتی» (Heteroassociative Networks)، «شبکههای بازگشتی» (Recurrent Networks) و «شبکههای ترکیبی» (Hybrid networks) هستند.
در این آموزش، شبکههای FFNN ،GRNN و CFNN را برای مدلسازی جریان خروجی آرایه فتوولتاییک انتخاب میکنیم. برای انتخاب بهترين مدل جهت این کار، شبكههای عصبی مختلف مانند CFNN و FFNN مقايسه شدهاند. این مدلها با استفاده از متلب تشکیل شده، آموزش دیده و اعتبارسنجی میشوند.
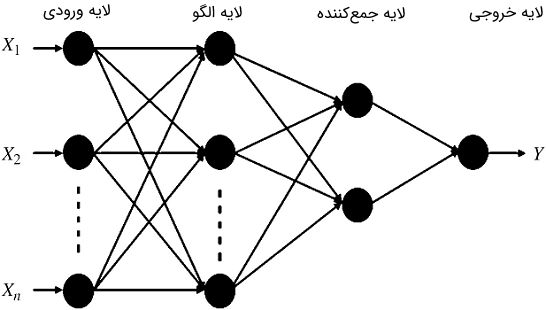
GRNN یک شبکه مبتنی بر احتمالات است. این شبکه وقتی متغیر هدف قطعی است طبقهبندی انجام میدهد، در حالی که وقتی متغیر هدف پیوسته باشد رگرسیون انجام میدهد. GRNNها شامل لایههای ورودی، الگو، جمعکننده و خروجی هستند. شکل ۱ نمودار کلی GRNN را نشان میدهد.
DFNN یک شبکه «خودسازمانده» و به نوعی شبیه FFNN است. هر دو شبکه مذکور از الگوریتم پسانتشار (BP) برای بهروزرسانی وزنها استفاده میکنند. شکل ۲ نمودار شماتیک کلی CFNN را نشان میدهد.
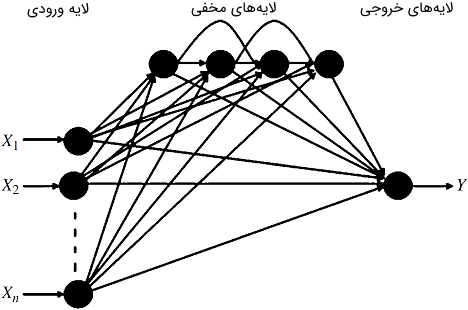
از سوی دیگر، شکل۳ نمودار شماتیک FFNN را نشان میدهد. این شبکه شامل لایههای ورودی، مخفی و خروجی است. پیشخور بدین معنی است که مقادیر فقط از لایه ورودی به لایه مخفی و سپس به لایههای خروجی حرکت میکنند.
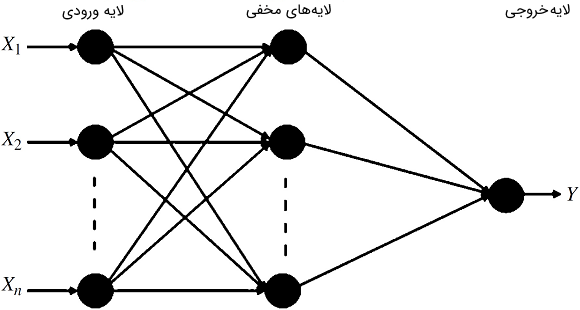
بدون آموزش دادن و تخمین خطای تعمیم، هیچ قاعده مستقیمی برای یافتن تعداد بهینه نرونهای مخفی وجود ندارد. با این حال، اگر تعداد نرونهای مخفی کم باشد، ممکن است کمبرازش رخ دهد که سبب خطای آموزش و خطای تعمیم بالا خواهد شد. هنگامی که تعداد زیادی نرون در لایه مخفی اعمال شود، بیشبرازش و واریانس بالا رخ میدهد. معمولاً تعداد گرههای مخفی را میتوان با برخی قوانین سرانگشتی به دست آورد. برای مثال، تعداد نرونهای لایه مخفی باید عددی بین اندازه لایه ورودی و اندازه لایه خروجی باشد. برخی نیز پیشنهاد کردهاند که تعداد نرونهای مخفی نباید بیش از دو برابر تعداد ورودیها باشد. در جایی دیگر توصیه شده که تعداد گرههای مخفی دو سوم یا 70 تا 90 درصد تعداد گرههای ورودی باشد. بر اساس پیشنهادهای فوق، تعداد نرونهای لایه مخفی مدلهای FFNN و CFNN برابر با دو گره مخفی در نظر گرفته شدهاند.
برای ارزیابی مدل پیشنهادی، از سه خطای آماری استفاده شده است که عبارتاند از: «درصد میانگین قدر مطلق خطا» (Mean Absolute Percentage Error) یا MAPE، «خطای انحراف میانگین» (Mean Bias Error) یا MBE و «خطای جذر میانگین مربعات» (Root Mean Square Error) یا RMSE.
دقت کلی یک شبکه عصبی را میتوان با MAPE بررسی کرد. MAPE به صورت زیر تعریف میشود:
$$ \large \mathrm { M A P E } = \dfrac { 1 } { n } \sum \limits _ { t = 1 } ^ { n } { \left \vert \dfrac { M - P } { M } \right \vert } $$
که در آن، $$M$$ دادههای اندازهگیری شده و $$P$$ دادههای پیشبینی شده هستند.
از سوی دیگر، شاخص انحراف میانگین مقادیر پیشبینی شده از دادههای اندازهگیری شده را میتوان با MBE بیان کرد. مقدار MBE مثبت نشان دهنده تخمین بیش از حد است. اطلاعات عملکرد طولانی مدت مدل شبکه عصبی نیز با MBE ارزیابی میشود. MBE را میتوان بهصورت زیر محاسبه کرد:
$$ \large \mathrm { M B E } = \dfrac { 1 } { n } \sum \limits _ { i = 1 } ^ { n } { ( P _ i - M _ i ) } $$
که در آن، $$M$$ دادههای اندازهگیریشده و $$P$$ دادههای پیشبینیشده هستند.
شاخص خطای آماری که در این آموزش استفاده میشود RMSE است. اطلاعات عملکرد کوتاهمدت مدل را میتوان با RMSE ارزیابی کرد. این، نشان دهنده اندازهگیری تغییرات دادههای پیشبینی شده حول دادههای اندازهگیری شده است. همچنین RMSE نشان دهنده بازدهی مدل تشکیل شده در پیشبینی مقادیر بعدی است. یک RMSE مثبت و بزرگ، انحراف بزرگ در دادههای پیشبینی شده از دادههای اندازهگیری شده را نشان میدهد. RMSE را میتوان با فرمول زیر محاسبه کرد:
$$ \large \mathrm { R MS E } = \sqrt { \dfrac { 1 } { n } \sum \limits _ { i = 1 } ^ { n } { ( P _ i - M _ i ) ^ 2 } } $$
مثال مدل سازی آرایه فتوولتاییک با شبکه عصبی
مدلی را در متلب تشکیل دهید که سه مدل فوق را با هم مقایسه کند. نتایج منبع دادههای «Source 2» را آزمایش و آنها را با مدلهای تجربی و آماری مقایسه کنید.
حل: برنامه زیر، پاسخ این مسئله است:
1clc
2%Modeling of PV systems using MATLAB
3fileName = PV Modeling Book Source.xls';
4sheetName = Source 2' ;
5G=xlsread(fileName, sheetName , 'A2:A36002');
6Temp=xlsread(fileName, sheetName , 'B2:B36002');
7I_PV=xlsread(fileName, sheetName , 'C2:C36002');
8%-------------------------------------------------------
9---G_Test=xlsread(fileName, sheetName , 'A36003:A43201');
10Temp_Test=xlsread(fileName, sheetName , 'B36003:B43201');
11I_PV_Test=xlsread(fileName, sheetName , 'C36003:C43201');
12%-----------------------ANNmodels-------------------------
13%---------inputs-------
14inputs = [G, Temp];
15I=inputs';
16targets= I_PV;
17T=targets';
18% %----------------------
19k=menu('chose the network type','FFANN','GRNN');
20if k==1;
21net = newff(I,T,5);
22end
23if k==2;
24net = newcf(I,T,2);
25end
26%---------------------
27Y = sim(net,I);
28net.trainParam.epochs = 100;
29net = train(net,I,T);
30test=[G_Test, Temp_Test];
31Test1=test';
32C_ANN1 = sim(net,Test1);
33C_ANN= C_ANN1';
34%========End of ANN=====================================
35%=======Theoretical current =========================
36C_th=(G_Test./1000)*7.91;
37%==============Regression==================================
38C_Reg=-1.17112+0.009*G+0.055*Temp;
39x_Reg=1:1:26;
40%========plotting results=============================
41plot(I_PV,'red')
42plot(C_ANN)
43hold on
44plot(C_Test, 'red');
45hold on
46plot(C_th, 'g')
47hold on
48plot (x_Reg,C_Reg)
49%----- ---------Modifying C_Test for Error calculation---
50---
51steps=5760;
52x_C_Test=C_Test;
53AV_C_Test=[];
54for i=1:steps:round(length(x_C_Test)/steps)*steps
55AV_C_Test=[AV_C_Test;sum(x_C_Test(i:i+steps-1))/
56steps];
57end
58AV_C_Test;
59%----- ---------Modifying C_ANN for Error calculation---
60----
61steps=5760;
62x_C_ANN=C_ANN;
63AV_C_ANN=[];
64for i=1:steps:round(length(x_C_ANN)/steps)*steps
65AV_C_ANN=[AV_C_ANN;sum(x_C_ANN(i:i+steps-1))/steps];
66end
67AV_C_ANN;
68%----------------------------------------------------------
69n_ANN = length(AV_C_ANN);
70E3_Hour=AV_C_Test-AV_C_ANN;
71ANN_MAPE= abs(E3_Hour./AV_C_Test);
72ANN_meanMAPE1 = sum(ANN_MAPE)/n_ANN;
73ANN_meanMAPE=ANN_meanMAPE1*100
74ANN_RMSE= sqrt(sum((AV_C_ANN-AV_C_Test).^2/n_ANN));
75ANN_MBE=sum(AV_C_ANN-AV_C_Test)/n_ANN;
76SUM=(sum(AV_C_ANN)./n_ANN);
77ANN_RMSE_Percentage =(ANN_RMSE/SUM)*100
78ANN_MBE_Percentage=(ANN_MBE/SUM)*100شکلهای زیر، حاصل از اجرای این برنامه هستند.
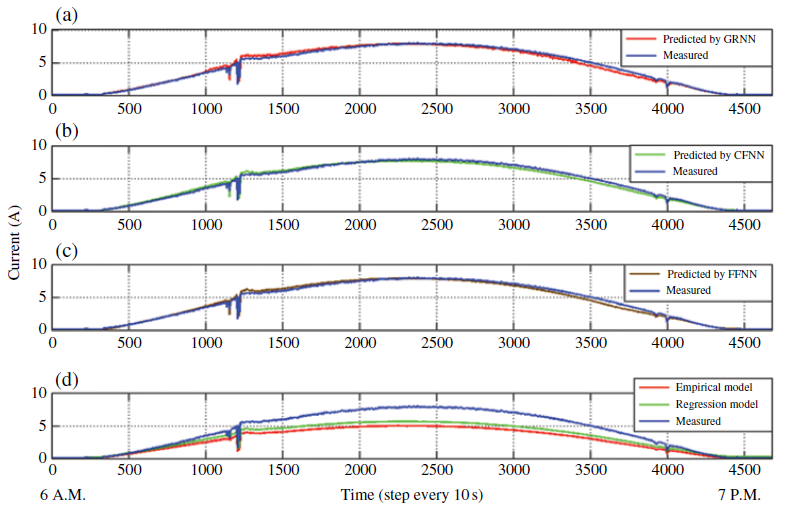
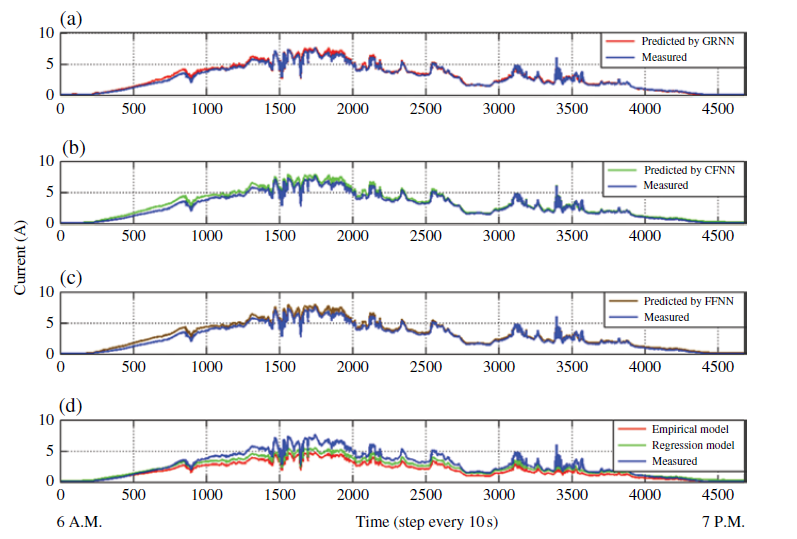
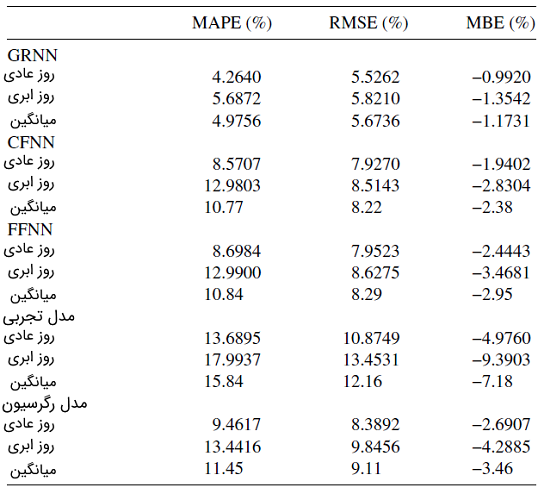
جدول زیر، ارزیابی آماری مدلها را نشان میدهد.
مدل سازی آرایه فتوولتاییک با الگوریتم جنگل تصادفی
در بخش قبل، مدلسازی توان خروجی سیستم فتوولتاییک با شبکههای عصبی انجام شد. این شبکهها میتوانند نامعینیهای خروجی سیستم را مدیریت کنند. با این حال، استفاده از شبکههای عصبی برای چنین هدفی، همراه با محدودیتها و چالشهایی مانند پیچیدگی فرایند آموزش، محاسبه نرونهای لایه مخفی و توانایی اداره دادههای بسیار نامعین است. برای حل این مشکل میتوان از برخی روشهای جدید با دقت و توانایی بالا در مدیریت دادههای بسیار نامعین مانند «مدلهای مبتنی بر جنگل تصادفی» (Random Forest-based Models) یا RF استفاده کرد.
مدل RF شامل درختهای تصمیم تصادفی و کیسهبندی است. «کیسهبندی» (Bagging) روشی برای کاهش واریانس تابع پیشبینی تخمینی است. درختهای تصمصم که از درختان ناهمبسته استفاده میکنند، تعمیمی از کیسهبندی هستند. سادهترین RFها با انتخاب گروه کوچکی از متغیرهای ورودی برای انشعاب تصادفی در هر گره تشکیل میشوند.
روش جنگل تصادفی، با ایجاد یک مجموعه جدید از مقادیر شروع میشود که با اندازه دادههای اصلی برابرند و به صورت تصادفی از مجموعه دادههای اصلی به وسیله خودراهاندازی یا بوتاسترپ انتخاب میشوند. پس از آن، دادههای جدید به صورت دنبالهای از انشعابات باینری (دوتایی) برای ایجاد درختهای تصمیم مرتب میشوند. در هر گرهای از این درختها، انشعاب با انتخاب مقدار و متغیر با خطای کمینه محاسبه میشود. در پایان، یک میانگین ساده از پیشبینهای تجمعی برای پیشبینی رگرسیون و یک رأی اکثریت ساده برای پیشبینی در طبقهبندی گرفته میشود.
تکنیکهای تجمعی خودراهانداز با دقت پیشبینی تقویت میشوند و تعیین میزان خطا و اهمیت متغیر را ممکن میسازند. میزان خطا و اهمیت متغیر با حذف مقادیر هر نمونه خودراهانداز محاسبه میشوند که دادههای «خارج از کیسه» (Out-of-bag) یا OOB نام دارند. دادههای OOB نقش اصلی را در رشد درخت ایفا میکنند، بدین معنی که این دادهها با مقادیر پیشبینی شده در هر مرحله مقایسه میشوند. در این روش، میزانهای خطا به دست آمده و از OOB نیز برای تعیین اهمیت متغیر استفاده میشود.
طبقهبندی و رگرسیون
درختهای طبقهبندی و رگرسیون پاسخهای پیشبینی شده به دادهها هستند. هنگام پیشبینی پاسخ، تصمیم، هر درخت را از گره اصلی به یک گره برگ در جنگل هدایت میکند که حاوی پاسخ است. درختهای رگرسیون پاسخ را به شکل عددی و درختهای طبقهبندی آن را به صورت اسمی (درست یا غلط) بیان میکنند.
جنگلهای تصادفی، بسته به درختهای طبقهبندی و رگرسیون ایجاد شده تغییر میکنند و طی مراحل زیر ساخته میشوند. در مرحله اول، همه دادههای ورودی برای آزمایش تمام انشعابات دوتایی ممکن در هر پیشبین استفاده شده، سپس انشعابی انتخاب میشود که بهترین مقیاس بهینهسازی را دارد. در مرحله دوم، انشعاب انتخاب شده به دو گره فرزند جدید تقسیم میشود. این فرایند برای گرههای فرزند جدید تکرار میشود.
اما دو مورد مقیاس بهینهسازی و دستور توقف برای کامل کردن فرایند قبل لازم است. مقیاس بهینهسازی مشخص میکند که انشعاب انتخابی برای کمینه «میانگین مربعات خطا» (Mean Square Error) یا MSE دادههای پیشبینی نسبت به دادههای آموزشی باید بررسی شود. در مقابل، در درختهای طبقهبندی، یکی از سه روش «شاخص تنوع جینی» (Gini’s Diversity Index) انحراف یا «قانون تقسیمبندی دوحالتی» (Towing Rule) برای انتخاب انشعاب به کار میرود.
طبقهبندی فرایندی است که در آن موضوعات شناخته، درک و متمایز میشوند. این فرایند، موضوعات را به صورت دستههای مستقل برای اهداف خاص دستهبندی میکند. طبقهبندی، فهم روابط بین موضوعات و زیرموضوعات را فراهم میکند. این فرایند در زبان، استنباط، تصمیمگیری، پیشبینی و انواع برهمکنش محیطی به کار میرود. طبقهبندی مانند رگرسیون در یادگیری ماشین نقش دارد.
رگرسیون یک فرایند آماری برای تعیین روابط بین متغیرهاست. هنگامی که روابط بین یک متغیر وابسته (یا یک «متغیر معیار») و یک یا چند متغیر مستقل بررسی میشوند، تکنیکهای بسیاری برای مدلسازی و تحلیل در رگرسیون گنجانده میشود.
از رگرسیون برای پیشبینی استفاده میشود و در طبقهبندی با یادگیری ماشین اشتراک دارد. در جنگلهای تصادفی، رگرسیون با رشد هر درخت مربوط به یک بردار تصادفی تشکیل میشود. مقادیر خروجی، عددی هستند. پیشبین درخت تصمیم با میانگینگیری از همه درختهای جنگل ساخته میشود.
الگوریتم رگرسیون
الگوریتم جنگل تصادفی، ترکیبی از مراحل آموزش و آزمایش است. در مرحلهٔ آموزش، الگوریتم، $$N$$ نمونه خودراهانداز را از دادههای آموزش اصلی رسم میکند و سپس تعدادی از درختهای رگرسیون یا طبقهبندی هرس نشده (Unpruned) یا CART را برای هر نمونه خودراهانداز ایجاد میکند. بهترین انشعاب صرفاً از نمونه تصادفی پیشبینها در هر گرهای از CART جدا (انتخاب) شده و انشعابی انتخاب میشود که خطا را به حداقل میرساند.
در هر تکرار خودراهانداز، دادهها با استفاده از تکنیک رشد درخت با نمونه خودراهانداز پیشبینی میشوند. میزان خطا برای هر پیشبین و پیشبینیهای OBB تجمعی محاسبه میشوند. اکنون گرههای پایانی دادههای جدیدی دارند که با تعیین میانگین تجمعی پیشبینها از میان تمام درختها پیشبینی میشوند. خطای درخت جنگل تصادفی به دو پارامتر وابسته است: همبستگی بین هر دو درخت و استحکام (مقاومت) هر درخت به صورت مجزا. هنگامی که مجموعه آموزشی یک درخت به وسیله نمونهبرداری رسم میشود، تعداد متغیرهای هر سطح در بهبود عملکرد مهم هستند. شکل ۶ مراحل اصلی الگوریتم جنگل تصادفی را نشان میدهد.
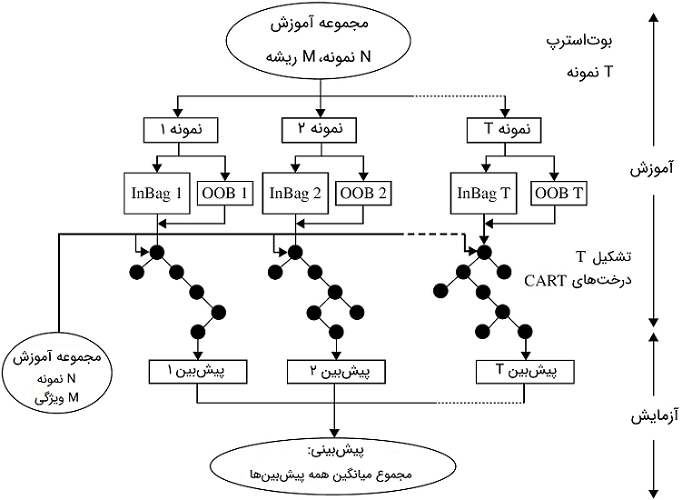
وقتی مجموعه آموزش به وسیله نمونهبرداری برای یک درخت خاص رسم میشود، از حدود یکسوم نمونههای مجموعه چشمپوشی خواهد شد. این نمونهها دادههای OBB نامیده شده و برای تخمین اهمیت متغیر و ساختار داخلی دادهها (اندازه نزدیکی) بهکار میروند. در اینجا، $$\beta ^{(t)}$$ نمونههای داخل کیسه برای درخت خاص $$t$$ و $$\beta ^{c(t)}$$ نمونههای مکمل برای همان درخت را نمایش میدهد.
علاوه بر الگوریتم رگرسیون، جنگلهای تصادفی، اندازهگیری قابل توجهی از اهمیت متغیر (اثرات خاص ورودیها روی خروجی) بر اساس دادههای OOB و نیز اندازهگیری اهمیت-تغییر انجام میدهند. اهمیت هر متغیر را میتوان با تغییر تمام مقادیر متغیر $$f$$ در نمونههای OOB برای هر درخت به صورت تصادفی به دست آورد. اندازهگیری اهمیت متغیر به صورت اختلاف بین دقتهای پیشبینی قبل و بعد از تغییر متغیر $$f$$ محاسبه میشود که روی تمام پیشبینها میانگین گرفته است. وقتی اهمیت متغیر کاهش یابد، دقت پیشبینی زیاد میشود. مقدار اهمیت هر متغیر با میانگین اهمیت تمام درختها با استفاده از رابطه زیر به دست میآید:
$$ \large {
V I ^ { ( t ) } ( f ) = \dfrac { \sum _ { T } { ( \dfrac { \sum _ { x _ i \in \beta ^ { c ( t ) } } { I \left ( L _ j = { c _ i } ^ { ( t ) } \right ) } } { \left \vert \beta ^ { c ( t ) } \right \vert }
- \dfrac { \sum _ { x _ i \in \beta ^ { c ( t ) } } { I \left ( L _ j = { c _ { i , \pi f } } ^ { ( t ) } \right ) } } { \left \vert \beta ^ { c ( t ) } \right \vert} ) } } { T } } $$
که در آن، $$\beta ^{c(t)}$$ متناظر با نمونههای خارج از کیسه برای یک درخت خاص، $$t$$ تعداد درختها ($$1, 2, \cdots, T$$) و $$T$$ تعداد کل درختهاست. همچنین $$c_i^{(t)}$$ و $$c_{i,\pi f}^{(t)}$$ دستههای پیشبینی شده برای هر نمونه مربوط به یک درخت قبل و بعد از تغییر متغیر هستند. پارامتر $$x_i$$ مقدار نمونه و $$L_j$$ برچسب درستی است که هردوی آنها در مرحله آموزش هستند.
پیشبینی جریان خروجی یک سیستم فتوولتاییک، با تنظیم اولیه متغیرها و نمونههای ورودی در الگوریتم کیسهپرکن شروع میشود. در اینجا، ورودیها تابش خورشید، دمای محیط، شماره روز، ساعت، عرض جغرافیایی، طول جغرافیایی و تعداد ماژولها هستند. در حقیقت، با هیچ فرمول ریاضی نمیتوان تعداد بهینه درختها را تنظیم کرد. تعداد درختها نصف تعداد نمونهها فرض میشود و تعداد برگهای هر درخت به صورت پیشفرض 5 است.
مثال مدل سازی آرایه فتوولتاییک با الگوریتم جنگل تصادفی
جریان خروجی سیستم فتوولتاییک مثال قبل را با استفاده از مدل جنگل تصادفی پیشبینی کرده و آن را با مدل مبتنی بر شبکه عصبی مقایسه کنید.
حل: برنامه جنگل تصادفی، با تعریف متغیرهای الگوریتم از قبیل شماره روز، تعداد ساعات در روز، دمای محیط، عرض جغرافیایی، طول جغرافیایی و تعداد ماژولها به عنوان ورودیها و جریان خروجی فتوولتاییک به عنوان خروجی شروع میشود. در مرحله نخست، برنامه مهمترین متغیرهای مؤثر بر خروجی را جستوجو میکند. در عین حال، دورافتادهها و خوشههای دادههای تشخیص داده میشوند. تعداد درختها برابر با نصف کل تعداد مشاهدات فرض میشود.
برنامه متلب این مثال به صورت زیر است.
1%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
2%%Random Forests-Regression --- Prediction - First Stage
3%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
4%%%
5%%((TRAINING STAGE))%%
6fileName = PV Modeling Book Source.xls';
7sheetName = Source 3' ;
8DN= xlsread(fileName, sheetName, 'B3:B1884'); %Day Number
9H= xlsread(fileName, sheetName, 'C3:C1884'); %Hour
10T= xlsread(fileName, sheetName, ’D3:D1884’); %Ambient
11Temp (°C)
12S= xlsread(fileName, sheetName, 'E3:E1884'); %Solar
13Radiation
14La= xlsread(fileName, sheetName, 'F3:F1884'); %Latitude
15Lo= xlsread(fileName, sheetName, 'G3:G1884'); %Longitude
16NPV= xlsread(fileName, sheetName, 'H3:H1884'); %Number
17of PV Modules
18I= xlsread(fileName, sheetName, 'J3:J1884'); %PV DC
19Current (A)
20%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
21%%%%%RF_Training Code
22ticID=tic;
23Y=[I]; %Split data into response array
24X=[DN,H,T,S,La,Lo,NPV]; %Split data into predictor array
25t=125; %Trees Number
26B=TreeBagger(t,X,Y,'method','regression','oobpred','on');
27%Estimating Variable Importance
28B=TreeBagger(t,X,Y,'method','regression','oobvarimp','on');
29figure(1);
30plot(oobError(B));
31xlabel('Number of Grown Trees');
32ylabel('Out-of-Bag Mean Squared Error');
33%%Most Important Variables
34figure(2);
35bar(B.OOBPermutedVarDeltaError);
36title('Variable Importance');
37xlabel('Variable Number');
38ylabel('Out-of-Bag Variable Importance');
39legend({'1: Day Number, 2: Hour, 3: Ambient Temp, 4:
40Solar Radiation, 5: Latitude, 6: Longitude, 7: # of PV
41Modules'},'Location','NorthEast');
42nidx = find(B.OOBPermutedVarDeltaError<0.65); %Imposing
43an arbitrary cutoff at 0.65 - Not Important Variables
44%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
45%%%
46%%Fraction of in-Bag Observation "Which observations are
47out of bag for which trees"
48finbag = zeros(1,B.NTrees);
49for t=1:B.NTrees
50finbag(t)=sum(all(~B.OOBIndices(:,1:t),2));
51end
52finbag = finbag/size(X,1);
53figure(3);
54plot(finbag);
55xlabel('Number of Grown Trees');
56ylabel('Fraction of in-Bag Observations');
57%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
58%%%
59%%Finding The Outliers
60BI=fillProximities(B); %Proximity Matrix that used
61figure(4);
62hist(BI.OutlierMeasure);
63title('The Outliers');
64xlabel('Outlier Measure');
65ylabel('Number of Observations');
66%%Discovering Clusters in the Data
67figure(5);
68[~,e] = mdsProx(BI,'colors','k');
69title('Cluster Analysis');
70xlabel('1st Scaled Coordinate');
71ylabel('2nd Scaled Coordinate')
72%%Assess the Relative Importance of the scaled axes by
73plotting the first 20 eigenvalues
74figure(6);
75bar(e(1:20));
76xlabel('Scaled Coordinate Index');
77ylabel('Eigen Value');
78%Saving The compact version of the Ensemble
79compact(B);
80% ((TESTING STAGE))%%
81filename = 'Data.xlsx';
82sheet = 1;
83%Testing Data - Excel File
84DN_t= xlsread(filename, sheet, 'B1885:B2690');
85H_t= xlsread(filename, sheet, 'C1885:C2690'); %Hour
86T_t= xlsread(filename, sheet, 'D1885:D12690');
87S_t= xlsread(filename, sheet, 'E1885:E2690');
88La_t= xlsread(filename, sheet, 'F1885:F2690');
89Lo_t= xlsread(filename, sheet, 'G1885:G2690') ;
90NPV_t= xlsread(filename, sheet, 'H1885:H2690');
91I_t= xlsread(filename, sheet, 'J1885:J2690');
92%RF_Testing Code
93Xdata=[DN_t,H_t,T_t,S_t,La_t,Lo_t,NPV_t];
94[Yfit,node]= predict(B,Xdata);
95figure(7);
96plot (Yfit)
97hold on
98plot (I_t, 'red')
99xlabel('Time (H)');
100ylabel('Current (A)');
101legend({'I Predicted','I Actual'},'Location','NorthEast');
102title('I Predicted Vs I Actual');
103figure(8);
104E = I_t-Yfit;
105plot(E)
106xlabel('Time (H)');
107ylabel('Magnitude (A)');
108title('Error');
109toc(ticID);
110%RF-Performance
111%Mean Bias Error (MBE) or Mean Forecasting Error (MFE) in
112Amp. // Average Deviation Indicator
113MBE=(sum(I_t(:)-Yfit(:)))./numel(I_t);
114if MBE<0
115F='Over forecasted';
116elseif MBE>0
117F='Under Forecasted';
118elseif MBE==o
119F='Ideal Forecasted';
120end
121%Mean Absolute Percentage Error (MAPE) // Accuracy
122Indicator
123MAPE = ( a b s ( ( s u m ( ( I _ t ( : ) - Y f i t ( : ) ) . / I _ t ( : ) ) ) . /
124numel(I_t))).*100;
125%Root Mean Square Error (RMSE) in Amp. // Efficiency
126Indicator
127RMSE=sum((I_t(:)-Yfit(:)).^2)/numel(I_t);
128%Outputs
129n1=['M ean Bias Error (MBE): ',num2str(MBE),'(A)','
130{Average Deviation Indicator}'];
131n2=['Forecasting Status: ',F];
132n3=['M ean Absolute Percentage Error (MAPE):
133',num2str(MAPE),'%',' {Accuracy Indicator}'];
134n4=['Root Mean Square Error (RMSE): ',num2str(RMSE),'(A)','
135{Efficiency Indicator}'];
136disp(n1)
137disp(n2)
138disp(n3)
139disp(n4)در مرحله دوم، پس از آنکه متغیرهای مهم به دست آمدند، به عنوان ورودیها مرتب میشوند. در اینجا، یک بهینهسازی برای تعداد درختها و تعداد برگهای هر درخت با استفاده از یک روش تکراری و به ترتیب مبنی بر حداقل RMSE، زمان سپری شده، MAPE و MBE انجام میشود.
1%%Random Forests‐Regression ‐‐‐ Prediction – Second Stage
2%%((TRAINING STAGE))%%
3filename = 'Data.xlsx';
4sheet = 1;
5%Training Data - Excel File
6DN= xlsread(filename, sheet, 'B3:B1884');
7H= xlsread(filename, sheet, 'C3:C1884');
8T= xlsread(filename, sheet, 'D3:D1884');
9S= xlsread(filename, sheet, 'E3:E1884');
10I= xlsread(filename, sheet, 'J3:J1884');
11%Testing Data - Excel File
12DN_t= xlsread(filename, sheet, 'B1885:B2690');
13H_t= xlsread(filename, sheet, 'C1885:C2690');
14T_t= xl sread(filename, sheet, 'D1885:D12690'); S_t=
15xlsread(filename, sheet, 'E1885:E2690');
16I_t= xl sread(filename, sheet, 'J1885:J2690'); %PV
17DC Current (A)
18%%RF_Training Code
19Y=[I]; %Split data into response array
20X=[DN,H,T,S]; %Split data into predictor array
21Xdata=[DN_t,H_t,T_t,S_t];
22MBE=[];
23MAPE=[];
24RMSE=[];
25v=[];
26for t=1:1:500
27for l=1:1:100
28tic;
29B=TreeB agger(t,X,Y,'method','regression','oobpred','on',
30'oobvarimp','on','minleaf',l);
31%%Saving The compact version of the Ensemble
32compact(B);
33%((TESTING STAGE))%%
34%RF_Testing Code
35[Yfit,node]= predict(B,Xdata);
36v(t,l)=toc;
37E = I_t-Yfit;
38%RF-Performance
39%Mean B ias Error (MBE) or Mean Forecasting Error (MFE) in
40Amp. // Average Deviation Indicator
41MBE(t,l)=(sum(I_t(:)-Yfit(:)))./numel(I_t);
42if MBE<0
43F='Over forecasted';
44elseif MBE>0
45F='Under Forecasted';
46elseif MBE==0
47F='Ideal Forecasted';
48end
49%Mean Absolute Percentage Error (MAPE) // Accuracy
50Indicator
51MAPE = (abs((sum((I_t(:)-Yfit(:))./I_t(:)))./
52numel(I_t))).*100;
53MAPE(t,l)=(sum(abs(E(:))./(sum(I_t(:))))).*100;
54RMSE(t,l)=sum((I_t(:)-Yfit(:)).^2)/numel(I_t);
55end
56end
57%Best number of Trees and leaves
58filename = 'RF - NTrees - 5.xlsx';
59sheet = 1;
60%RF Results Data - Excel File
61NT = xlsread(filename, sheet, 'B2:B22'); %Trees
62Number
63ET = xlsread(filename, sheet, 'D2:D22'); %Elapsed
64time (Sec.)
65MBE = xlsread(filename, sheet, 'E2:E22'); %Mean
66Bias Error (MBE) (A)
67MAPE = xlsread(filename, sheet, 'G2:G22'); %Mean
68Absolute Percentage Error (MAPE) (%)
69RMSE= xlsread(filename, sheet, 'I2:I22'); %Root
70Mean Square Error (RMSE) (A)
71OOB= xlsread(filename, sheet, 'J2:J22'); %Out of Bag
72(OOB)
73%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
74%%%y=[0.03:0.015:0.08];
75for i=1:length(NT)
76figure(1);
77plot (NT,RMSE,'*-')
78xlabel('Number of Trees');
79ylabel('Root Mean Squared Error (A)');
80figure(2);
81plot (NT,ET,'*-')
82xlabel('Number of Trees');
83ylabel('Elapsed time (Sec.)');
84figure(3);
85plot (NT,MBE,'*-')
86xlabel('Number of Trees');
87ylabel('Mean Bias Error (MBE) (A)');
88figure(4);
89plot (NT,MAPE,'*-')
90xlabel('Number of Trees');
91ylabel('Mean Absolute Percentage Error (MAPE) (%)');
92figure(5);
93plot (NT,OOB,'*-')
94xlabel('Number of Trees');
95ylabel('Out of Bag (OOB))');
96end
97[M1,I1]=min(RMSE(:));
98[M2,I2]=min(ET(:));
99[M3,I3]=min(MAPE(:));
100[M4,I4]=min(MBE(:));
101[M5,I5]=min(OOB(:));
102n1=['M in. Root Mean Squared Error : ',num2str(M1),'(A)',' @
103index :', num2str(I1)];
104n2=['Min. Elapsed time : ',num2str(M2),'(Sec.)',' @ index:
105', num2str(I2)];
106n3=['Min. Mean Absolute Percentage Error (MAPE) :
107',num2str(M3),'(%)',' @ index :', num2str(I3)];
108n4=['Min. Mean Bias Error (MBE) : ',num2str(M4),'(A)',' @
109index :', num2str(I4)];
110n5=['Min. Out of Bag (OOB) data : ',num2str(M5),'(A)',' @
111index :', num2str(I5)];
112disp(n1)
113disp(n2)
114disp(n3)
115disp(n4)
116disp(n5)در مرحله سوم، مهمترین متغیرها و بهترین تعداد درختها و برگها در هر درخت مرتب میشوند. اکنون، برنامه برای آموزش و پیشبینی جریان خروجی فتوولتاییک آماده است.
1%%Random Forests‐Regression –— Prediction – Third Stage
2%%((TRAINING STAGE))%%
3filename = 'Data.xlsx';
4sheet = 1;
5%Training Data - Excel File
6DN= xlsread(filename, sheet, 'B3:B1884');
7H= xlsread(filename, sheet, 'C3:C1884');
8T= xlsread(filename, sheet, 'D3:D1884');
9S= xlsread(filename, sheet, 'E3:E1884');
10I= xlsread(filename, sheet, 'J3:J1884');
11%RF_Training Code
12Y=[I]; %Split data into response array
13X=[DN,H,T,S]; %Split data into predictor array
14t=65; %Trees Number
15i=1;
16B=TreeBagger(t,X,Y,'method','regression','oobvarimp','on
17','oobpred','on','minleaf',i);
18%Saving The compact version of the Ensemble
19compact(B);
20%((TESTING STAGE))%%
21filename = 'Data.xlsx';
22sheet = 1;
23%Testing Data - Excel File
24DN_t= xlsread(filename, sheet, 'B1885:B2690');
25H_t= xlsread(filename, sheet, 'C1885:C2690');
26T_t= xlsread(filename, sheet, 'D1885:D12690');
27S_t= xlsread(filename, sheet, 'E1885:E2690');
28I_t= xlsread(filename, sheet, 'J1885:J2690');
29%%RF_Testing Code
30Xdata=[DN_t,H_t,T_t,S_t];
31[Yfit,node]= predict(B,Xdata);
32figure(7);
33plot (Yfit)
34hold on
35plot (I_t, 'red')
36xlabel('Time (H)');
37ylabel('Current (A)');
38legend({'I Predicted','I Actual'},'Location','NorthE
39ast');
40title('I Predicted Vs I Actual');
41figure(8);
42E = I_t-Yfit;
43plot(E)
44xlabel('Time (H)');
45ylabel('Magnitude (A)');
46title('Error');
47%%RF-Performance
48%Mean Bias Error (MBE) or Mean Forecasting Error (MFE) in
49Amp. // Average Deviation Indicator
50MBE=(sum(I_t(:)-Yfit(:)))./numel(I_t);
51if MBE<0
52F='Over forecasted';
53elseif MBE>0
54F='Under Forecasted';
55elseif MBE==o
56F='Ideal Forecasted';
57end
58%Mean Absolute Percentage Error (MAPE) // Accuracy
59Indicator
60MAPE=(abs((sum((I_t(:)-Yfit(:))./I_t(:)))./
61numel(I_t))).*100;
62%MAPE=abs((sum((I_t(:)-Yfit(:))./I_t(:)))./numel(I_t));
63MAPE=(sum(abs(E(:))./(sum(I_t(:))))).*100;
64%Root Mean Square Error (RMSE) in Amp. // Efficiency
65Indicator
66RMSE=sum((I_t(:)-Yfit(:)).^2)/numel(I_t);
67%%Outputs
68n1=['Mean Bias Error(MBE): ',num2str(MBE),'(A)','
69{Average Deviation Indicator}'];
70n2=['Forecasting Status: ',F];
71n3=['Mean Absolute Percentage Error (MAPE): ',num2str(MAPE),
72'%',' {Accuracy Indicator}'];
73n4=['Root Mean Square Error (RMSE): ',num2str(RMSE),'(A)','
74{Efficiency Indicator}'];
75disp(n1)
76disp(n2)
77disp(n3)
78disp(n4)
79%%ANN Vs RF
80filename = 'Data.xlsx';
81sheet = 1;
82%Training Data - Excel File
83I= xls read(filename, sheet, 'L3:L808'); Iann=
84xlsread(filename, sheet, 'N3:N808');
85Irf= xlsread(filename, sheet, 'O3:O808');
86plot (I)
87hold on
88grid on
89plot (Iann, ':ks')
90hold on
91plot (Irf, '--ro')
92xlabel('Time (H)');
93ylabel('Current (A)');
94legend({'I Actual','I ANNs Model','I Random Forests
95Model'},'Location','NorthEast');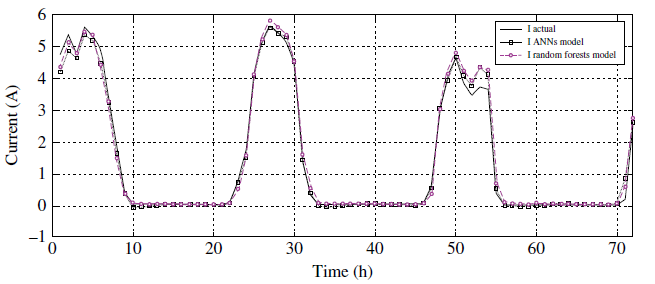
جدول زیر مقادیر آماری و زمان صرف شده روشهای شبکه عصبی و جنگل تصادفی را نشان میدهد.

مدل سازی آرایه فتوولتاییک با تکنیکهای جستوجوی اکتشافی
معادله خروجی سلول خورشیدی را میتوان با روشهای بسیاری از قبیل روش «نیوتون-رافسون» (Newton–Raphson) یا NR، الگوریتم «لونبرگ-مارکوارت» (Levenberg–Marquard) یا LM، روشهای مبتنی بر شبکه عصبی و روشهای عددی دیگر حل کرد. اخیراً روشهای اکتشافی از قبیل «الگوریتم ژنتیک» (Genetic Algorithm) یا GA، «بهینهسازی ازدحام ذرات» (Particle Swarm Optimization) یا PSO، «بهینهسازی جفتگیری پرنده» (Simplified Bird Mating Optimizer) یا SBMO، «تکامل تفاضلی» (Differential Evolution)، «الگوریتم بهینهسازی جستوجوی ممنوعه» (Tabu Search Optimization Algorithm)، «بهینهسازی آشوب موازی جهشی» (Mutative-scale Parallel Chaos Optimization Algorithm) یا MPCOA و الگوریتمهای تبرید شبیهسازیشده (Simulated Annealing) یا SA به علت بازده و قابلیت اطمینان بالا برای حل چنین مسائلی مورد استفاده قرار گرفتهاند.
از رابطه ۱ واضح است پارامترهایی که بر عملکرد ماژول فتوولتاییک تسلط دارند، $$I_\mathrm{Ph}$$، $$I_\mathrm{o}$$، $$R_\mathrm{s}$$، $$R_\mathrm{p}$$ و $$a$$ هستند. این پارامترها مجهول و به تابش خورشید و دمای سلول بستگی دارند. بنابراین، میتوان از یک الگوریتم بهینهسازی برای به دست آوردن مقادیر بهینه این پارامترها استفاده کرد. در اینجا، یک تابع هدف برای یافتن پارامترهای محاسبه شده مدل ماژول به صورت بهینه فرمولبندی میکنیم. تابع هدف به صورت RMSE است که تفاوت بین جریان محاسبه شده و تجربی را نشان میدهد. این تابع بهصورت زیر است:
$$ \large f ( \theta ) = \sqrt { \dfrac { 1 } { n } \sum \limits _ { i = 1 } ^ { n } { P ( v _ \mathrm { e } , I _ \mathrm { e } , \theta ) ^ 2 } } $$
که در آن:
$$ \large { { } ^ { }
P ( v _ \mathrm { e } , I _ \mathrm { e } , \theta ) = I _ \mathrm { e } - I _ \mathrm { p h } + I _ \mathrm { o } \left [ \mathrm { e x p } \left ( \dfrac { V _ \mathrm { e } + I _ \mathrm { p } R _ \mathrm { s } } { V _ \mathrm { t } } \right ) - 1 \right ] + \dfrac { V _ \mathrm { e } + I _ \mathrm { p } R _ \mathrm { s } } { R _ \mathrm { p } } } $$
و $$V _ \mathrm { e }$$ و $$I _ \mathrm { e }$$، به ترتیب، مقادیر تجربی ولتاژ و جریان صفحه فتوولتاییک هستند. همچنین، $$ \theta $$ برداری از پنج پارامتر ($$ I _ \mathrm { p h }$$، $$I _ \mathrm { o }$$، $$R _ \mathrm { s }$$، $$R _ \mathrm { p }$$ و $$ a $$) و $$ n $$ طول مجموعه داده است.
همانطور که بسیاری از پژوهشگران توصیه کردهاند که الگوریتمهای DE بیشترین کارایی را در حل چنین مسئلهای دارند، در اینجا نیز بر الگوریتم DE تمرکز میکنیم.
در الگوریتم DE رایج، الگوریتم جستجوی مستقیم مبتنی بر جمعیت که از مجموعه جمعیت اولیه $$ S $$ استفاده میکند، از بردارهای تکی NDبُعدی تشکیل میشود که به صورت تصادفی انتخاب شدهاند. این بردارهای منفرد توسط یک فرایند ادغام به منظور یافتن مقادیر بهینه که یک کمینهسازی سراسری را برآورده میکند، هدایت میشوند. ساز و کار اصلی فرایند جذب جایگزینی بردارهای تکی بد در جمعیت $$S$$ با بردارهای تکی بهتر در هر تکرار است.
الگوریتم DE شامل چهار مرحله ساده و پشت سر هم است که عبارتاند از مقداردهی اولیه، جهش، گذر و انتخاب. این الگوریتم مانند سایر الگوریتمهای جستوجوی مستقیم مبتنی بر جمعیت که از یک مجموعه جمعیت اولیه ($$S$$) استفاده میکند که به طور تصادفی به عنوان یک جواب انتخاب میشود. این شامل الگوریتم شامل $$N$$ بردار مجزا است و هر بردار شامل $$D$$ پارامتر است که برای بهینهسازی مورد نیاز است. سه مرحله آخر (جهش، گذر و انتخاب) در هر گام تکرار میشوند تا جواب اولیه برای رسیدن به حداکثر تعداد نسل $$ G _ \max$$ یا به دست آوردن مقدار برازندگی مورد نیاز، بهبود یابد. DEAM از بردارهای NDبعدی به عنوان یک مجموعه جمعیت ($$S$$) برای جستوجوی پارامترهای بهینه در فضای جستوجو استفاده میکند. مجموعه جمعیت به این صورت تعریف شده است:
$$ \large \begin {align}
S ^ G = \left [ X _ 1 ^ G , X _ 2 ^ G , . . . , X _ N ^ G \right ] = \left [ X _ i ^ G \right ]
\end {align} $$
که در آن:
$$ \large \begin {align}
X _ i = \left [ X _ { 1 , i } , X _ { 2 , i } , . . . , X _ { D , i } \right ] = \left [ X _ { j , i } \right ]
\end {align} $$
که $$ X _ i $$ بردار هدف نامیده میشود و $$ i $$ تعداد جوابهای کاندید جمعیت ($$i = 1 , 2 , ..., N$$)، $$ j $$ بعد بردار تکی ($$j= 1 , 2 , ... , D$$) و $$ G $$ اندیس نسل ($$ G = 1 , 2 , ... , G _\max$$) است.
شکل ۶ الگوریتم پیشنهادی را نشان میدهد. مراحل این الگوریتم در ادامه توضیح داده شدهاند.
مقداردهی اولیه: فرایند بهینهسازی با ایجاد یک جمعیت اولیه آغاز میشود: $$ S ^ G = [X _ i ^ G ] $$ و $$ G = 0$$. مقادیر اولیه $$D$$ پارامتر به طور تصادفی انتخاب و به صورت یکنواخت در ناحیه جستوجو توزیع میشوند. ناحیه جستوجو به ترتیب با کرانهای پایین و بالای $$ X _{j,L}$$ و $$X_{j,H}$$ محدود میشود. بردار تکی مقدار اولیه به صورت زیر انتخاب شده است:
$$ \large X _ { j , i } ^ 0 = X _ { j , L , i } + \mathrm {rand}( X _ { j , H , i } - X _ { j , L , i } ) $$
که rand یک عدد تصادفی در بازه $$[0,1] $$ است.
جهش: DEAM مقدار $$ M_d $$ یا $$ M_e $$ را در یک تکرار فراخوانی میکند. معیاری که برای جابهجایی بین هر دو نوع جهش استفاده میشود، این است:
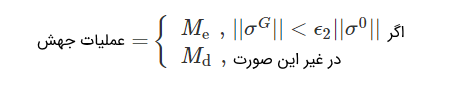
که $$||\sigma ^ G ||$$ و $$ ||\sigma ^ 0 || $$ نرم بردارهای انحراف معیار بردارهای سطری جمعیت $$ S $$ برای $$ G $$ و نسل اولیه هستند و $$ \epsilon _ 2 $$ یک پارامتر سوئیچینگ است که برای سوئیچ بین عملیات $$ M_ d $$ و $$ M _ e $$ به کار میرود و $$ \epsilon \in [0,1] $$. برای هر بردار هدف $$ X _ i ^ G $$، یک بردار جهش $$ \hat {X}_ i ^ G $$ بر اساس عملیات $$ M _ d $$ به صورت زیر تولید میشود:
$$ \large \hat { X } _ i ^ G = X _ \alpha ^ G + F \left ( X _ \beta ^ G - X _ \gamma ^ G \right ) $$
که بردارهای $$ X _ \alpha ^ G $$، $$ X _ \beta ^ G $$ و $$ X _ \gamma ^ G $$ بردارهایی هستند که به صورت تصادفی از جمعیت انتخاب میشوند و $$ \alpha $$، $$\beta$$ و $$ \gamma$$ شاخصهای مجزایی هستند که به بازه $$ [1,N] $$ تعلق دارند. بردار $$ X _ \alpha ^ G $$ بردار پایه نامیده میشود و $$F $$ پارامتر کنترل مقیاس جهش است که معمولاً در بازه $$[0.5, 1 ] $$ انتخاب میشود.
در همین حال، عملیات جهش $$M_e$$ نیز بر اساس سه بردار مجزا است که به طور تصادفی از بین جمعیت انتخاب میشوند، اما بر خلاف $$M_d$$، شاخص یکی از این بردارها ممکن است همان شاخص بردار فعلی باشد. عملیات $$M_e$$ از کل نیروی وارده بر یک بردار منفرد $$X_\alpha ^ G $$ توسط دو بردار دیگر $$X_ \beta ^ G $$ و $$ X _ \gamma ^ G $$ استفاده میکند. مانند الگوریتم EM، نیروی اعمال شده بر $$X_\alpha ^ G $$ توسط $$X_ \beta ^ G $$ و $$ X _ \gamma ^ G $$ بر اساس بارهای بین بردارهای زیر محاسبه میشود:
$$ \large q _ { \alpha \beta } ^ G = \dfrac { f \left ( X _ \alpha ^ G \right ) - f \left ( X _ \beta ^ G \right ) } { f \left ( X _ \mathrm { w } ^ G \right ) - f \left ( X _ \mathrm { b } ^ G \right ) } $$
$$ \large q _ { \alpha \gamma } ^ G = \dfrac { f \left ( X _ \alpha ^ G \right ) - f \left ( X _ \gamma ^ G \right ) }{ f \left ( X _ \mathrm { w } ^ G \right ) - f \left ( X _ \mathrm { b } ^ G \right ) } $$
که $$ f ( X ) $$ مقدار تابع هدف برای بردار تکی $$ x $$ است و $$ X _ b ^ G $$ و $$ X _ w ^ G $$، به ترتیب، بهترین و بدترین بردارهای تکی هستند که مقادیر بهترین و بدترین تابع هدف را برای نسل $$G$$اُم رقم میزنند. $$ G $$ نیز شاخصی است که به تعداد نسل بر میگردد ($$G = 1 , 2 , ... , G _ \max $$). نیروی اعمال شده بر $$ X _ \alpha ^ G $$ توسط $$ X _ \beta ^ G $$ و $$ X _ \gamma ^ G $$ به صورت زیر محاسبه میشود:
$$ \large F _ { \alpha \beta } ^ G = \left ( X _ \beta ^ G -X _ \alpha ^ G \right ) q _ { \alpha \beta } ^ G $$
$$ \large F _ { \alpha \gamma } ^ G = \left ( X _ \gamma ^ G -X _ \alpha ^ G \right ) q _ { \alpha \gamma } ^ G $$
در نتیجه، نیروی اعمالی بر $$ X _ \alpha ^ G $$ توسط $$ X _ \beta ^ G $$ و $$ X _ \gamma ^ G $$ به شکل زیر محاسبه میشود:
$$ \large F _ { \alpha } ^ G = F _ { \alpha \beta } ^ G + F _ { \alpha \gamma } ^ G $$
سپس، بردار جهش عملیات $$ M _ e $$ به صورت زیر محاسبه میشود:
$$ \large \hat { X } _ i ^ G = X _ \alpha ^ G + F _ \alpha ^ G $$
گذر: مرحله گذر DEAM مشابه همانی است که در الگوریتم DE وجود دارد. در این مرحله، هر دو بردار هدف $$ X _ i ^ G $$ و بردار جهش $$ \hat { X} _ i ^ G $$ برای تولید بردار آزمایش $$ y _ { j , i } ^ G $$ به کار میروند که به صورت زیر بیان میشود:

که $$\text{rand}$$ یک عدد تصادفی در بازه $$(0,1)$$ است. همچنین، $$ I_ i $$ یک شاخص تصادفی در بازه $$[1,D]$$ و $$ \text{CR}\in [0.5 , 1 ] $$ پارامتر کنترل گذر است. بردار آزمایش برابر با بردار جهش $$\text{CR}=1$$ است.
پارامترهای بردار آزمایشی را در صورتی که خارج از فضای مجاز جستوجو باشد، بررسی کرد تا اطمینان حاصل شود که مقادیر پارامتر مقادیر فیزیکی هستند. اگر هر پارامتر خارج از حد مجاز فضای جستوجو باشد، با مقدار جدید به شرح زیر جایگزین میشود:
$$ \large y _ { j , i } ^ G = X _ { j , L , i } + \mathrm {rand} ( X _ { j , H , i } - X _ { j , L , i } ) $$
انتخاب: مرحله انتخاب پس از تولید بردارهای آزمایشی N اعمال میشود. روند انتخاب بین بردارهای هدف فعلی و آزمایشی براساس مقادیر تابع هدف برای هر دو بردار است. برداری كه تابع هدف كوچكی دارد، به عنوان عضوی از جمعیت برای نسل بعدی $$ G + 1 $$ انتخاب میشود. روند انتخاب را میتوان به این صورت توصیف کرد:
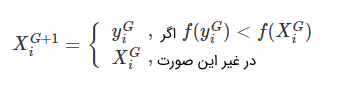
سرانجام، بازتولید بردارهای آزمایش (جهش و گذر) و مراحل انتخاب تا رسیدن به شرایط توقف از پیش تعیین شده ادامه دارد.
مثال مدل سازی آرایه فتوولتاییک با تکنیکهای جستوجوی اکتشافی
برنامهای بنویسید که با استفاده از الگوریتم DE ماژول جدول زیر را به صورت بهینه مشخص کند.
حل: برای حل این مسئله، چهار ام فایل متلب مورد نیاز است. اولین مورد برای به دست آوردن مقدار پنج پارامتر استفاده میشود. در این برنامه، مقادیر تابش خورشید و دمای سلول به دست میآید. علاوه بر این، جریان و ولتاژ آزمایشی (برای منحنی I-V) نیز به دست میآیند. پس از آن، برنامه دوم به عنوان یک تابع MATLAB برای پیادهسازی الگوریتم DE فراخوانی میشود و مقادیر بهینه پنج پارامتر را در شرایط خاص آبوهوایی برمیگرداند. سپس مشخصات I-V و P-V برای شرایط خاص آبوهوایی با استفاده از روش NR به دست میآید. پس از آن، عملکرد برازندگی الگوریتمهای DE در هر نسل اعمال میشود.
برنامههای مذکور در ادامه آورده شدهاند:
1%%%% algorithm for optimizing the 3-parameters of PV
2module (a, Rs, Rp, Iph, Io),
3%%%% Plotting I-V & P-V characteristics and comparing the
4calculation and
5%%%% experimental characteristics
6clc;
7clear all;
8close all;
9t=cputime;
10radiation=[978];
11%///&&&Array of solar radiation in (w/m^2)///&&&%
12cell_temperature=[328.56]; %///&&&Array
13of ambient temperature in (K)///&&&%
14sheet=7;
15%%%%%%%% Reading the experimental voltage and current
16data %%%%%%%%
17Ve=xlsread('PV modeling book data source.xls',Source 4,'
18G3:G104'); %///&&&Reading
19the experimental voltage///&&&%
20Ie=xlsread('PV modeling book data source.xls', Source 4,'
21H3:H104'); %///&&&Reading
22the experimental current///&&&%
23save ('var_fitness_function', 'Vp','Ie');
24solar_radiation=radiation./1000; %Array of solar
25radiation in (kw/m^2)
26%a_best=zeros(size(radiation)); %Array for the best
27diode ideality factor
28%Rs_best=zeros(size(radiation)); %Array for the best PV
29series resistance
30%Rp_best=zeros(size(radiation)); %Array for the best PV
31parallel resistance
32%f_best=zeros(size(radiation)); %Array for the best
33overall fitness function
34G=solar_radiation; %Reading the solar
35radiation values one by one
36Tc=cell_temperature; %Reading the ambient
37temperature values one by one
38[f_bestt,a_bestt,Rs_bestt,Rp_bestt, Iph_bestt,
39Io_bestt]=. . .
40PV_MODELING_BASED_DE_ALGORITHM (G,Tc); %Call 5
41parameter DE-optimization function
42%f_bestt
43%a_bestt
44%Rs_bestt
45%Rp_bestt
46a_best=a_bestt; %Array for the best
47diode ideality factor
48Rs_best=Rs_bestt; %Array for the best
49PV series resistance
50Rp_best=Rp_bestt; %Array for the best
51PV parallel resistance
52Iph_best=Iph_bestt; %Array for the best
53photo current
54Io_best=Io_bestt; %Array for the best
55diode saturation current
56f_best=f_bestt; %Array for the best
57overall fitness function
58%f_best
59%a_best
60%Rs_best
61%Rp_best
62%%%%%%%%%//// Computing I-V c/c of PV module////%%%%%%%%
63%%%%%%%%%%%%%%%%%%%%%% Declaration the constants
64%%%%%%%%%%%%%%%%%%%%%%%%%%
65Nsc=36; %Number of cells are
66connected in series per module
67k=1.3806503*10^-23; %Boltzmann constant (J/K)
68q=1.60217646*10^-19; %Electron charge in
69(Coulomb)
70VT=(Nsc*k*Tc)/q; %Diode thermal voltage (v)
71%%%%%%%%//// Computing the theoretical current using NR
72method ////%%%%%%%%
73Ip=zeros(size(Vp));
74for h=1:5
75Ip=Ip ‐ ((Iph_best‐Ip‐Io_best.*(exp((Vp+Ip.*Rs_best)./
76(a_best.*VT))‐1)‐…
77((Vp+Ip.*Rs_best)./Rp_best))./(‐1‐Io_best.*(Rs_
78best./(a_best.*VT)).* …
79exp((Vp+Ip.*Rs_best)./(a_best.*VT))-(Rs_best./
80Rp_best)));
81end
82%%%%%%%%%%%%%%%%%%%%%//// PLOTTING I-V CHARACTERISTIC
83////%%%%%%%%%%%%%%%%%
84%load IV_characteristic_data_experimental
85figure
86hold on
87plot(Vp,Ip,Ve,Ie,'o')
88hold off
89title('I-V characteristics of PV module with solar radiation
90and ambient temperature variations')
91xlabel('Module voltage (v)')
92ylabel('Module current(A)')
93%for z=1:length(G)
94gtext('978 W/m^2, 328.56 K') %///&&&solar
95radiation in (w/m^2) and cell temperature in (K)///&&&%
96%end
97%%%%%%%%%%%%%%%%%%%//// COMPUTING THE PV MODULE POWER
98////%%%%%%%%%%%%%%%%%
99Pp=Vp.*Ip; %Computing the theoretical
100PV module power
101Pe=Vp.*Ie; %Computing the experimental
102PV module power
103%%%%%%%%%%%%%%%%%%%%%//// PLOTTING P-V CHARACTERISTIC
104////%%%%%%%%%%%%%%%%%
105figure
106hold on
107plot(Vp,Pp,Vp,Pe,'o')
108hold off
109title('P-V characteristics of PV module')
110xlabel('Module voltage (v)')
111ylabel('Module power(w)')
112%for z=1:length(G)
113gtext('978 W/m^2, 328.56 K') %///&&&solar
114radiation in (w/m^2) and cell temperature in (K)///&&&%
115%end
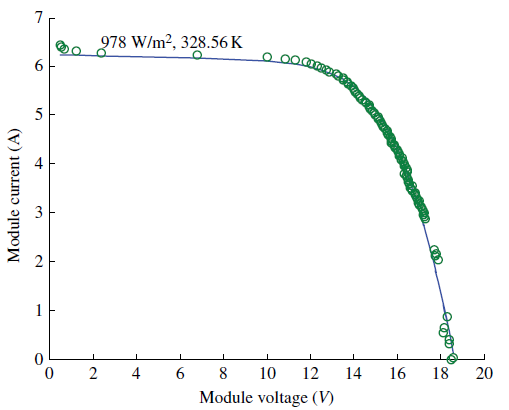
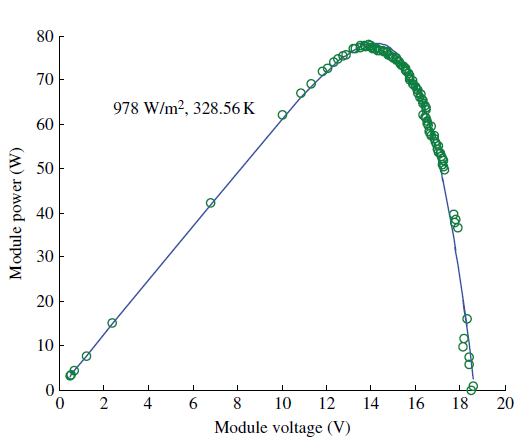
116%%%%%%%%%%%%%%%%%//// COMPUTING THE ERROR////%%%%%%%%%%%
117Iee=(1/length(Vp))*(sum(Ie));
118RMSE=sqrt((1/length(Vp))*sum((Ip-Ie).^2))
119MBE=(1/length(Vp))*sum((Ip-Ie).^2)
120RR=1-((sum((Ie-Ip).^2))/(sum((Ie-Iee).^2)))
121%%%% MATLAB Script function of Differential Evolution
122(DE)algorithm
123%%%% for optimizing the 5-PV-parameters (a, Rs, Rp, Iph &
124Io)
125%%%% Date 16/3/2015 - Monday
126function [f_bestt,a_bestt,Rs_bestt,Rp_bestt,Iph_bestt,
127Io_bestt]=. . .
128PV_MODELING_BASED_DE_ALGORITHM (G,Tc) %Define a
129function to optimize the 3-PV-parameters
130%%%%%%%%%%%%%%%%%//// Control parameter declaration
131////%%%%%%%%%%%%%%%%%%%
132EP=0.054;
133D=5; %Dimension
134of problem (5-parameters of PV module)
135Np=10*D; %///&&&Size
136of population (number of individuals)///&&&
137%%%%%%%%%%%%%%%%%%%%%%%%%%Mutation factor
138%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
139F=0.85; %///&&&Mutation
140factor///&&&
141%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%Crossover
142rate%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
143CR=0.6; %///&&&Crossover
144rate factor///&&&
145%%%%%%%%%%%%%%%%%%%%Maximum number of generation
146(iteration)%%%%%%%%%%%%%%%
147GEN_max=500; %///&&&Maximum
148generation number///&&&
149%%%%%%%%%%%%%%%%%%%%//// SAVING RESULTS IN MAT FILE
150////%%%%%%%%%%%%%%%%%%%
151sheet=7; %///&&&No.
152of sheet to save results///&&&%
153file_name='Results_of_Radiation_7_temperature_7.mat';
154%///&&&Name of file to save results in MAT file///&&&%
155save (file_name,'Np','GEN_max','F','CR');
156%%%%%%%%%%%%%%%%%%%%//// SAVING RESULTS IN EXCEL FILE
157////%%%%%%%%%%%%%%%%%%%
158xlswrite ('PVM4_Try_3.xlsx',Np,sheet,'P5');
159xlswrite ('PVM4_Try_3.xlsx',GEN_max,sheet,'Q5');
160xlswrite ('PVM4_Try_3.xlsx',F,sheet,'R5');
161xlswrite ('PVM4_Try_3.xlsx',CR,sheet,'S5');
162xlswrite ('PVM4_Try_3.xlsx',EP,sheet,'U5');
163%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
164%%%%%%%%%%%%%%%%%%%
165Rs_l=0.1; %Lower limit of series
166resistance (Rs)
167Rs_h=2; %Upper limit of series
168resistance (Rs)
169Rp_l=100; %Lower limit of parallel
170resistance (Rp)
171Rp_h=5000; %Upper limit of parallel
172resistance (Rp)
173a_l=1; %Lower limit of diode
174ideality factor (a)
175a_h=2; %Upper limit of diode
176ideality factor (a)
177Iph_l=1; %Lower limit of photo
178current (Iph)
179Iph_h=8; %Upper limit of photo
180current (Iph)
181Io_l=1e-12; %Lower limit of diode
182saturation current (Io)
183Io_h=1e-5; %Upper limit of diode
184saturation current (Io)
185L=[a_l Rs_l Rp_l Iph_l Io_l]; %Define lower limit
186vector of 5-PV-parameters
187H=[a_h Rs_h Rp_h Iph_h Io_h]; %Define upper limit
188vector of 5-PV-parameters
189%%%%%%%%%%%%%%%Number of times the algorithm is
190repeated%%%%%%%%%%%%%%%%%%%
191rr=1;
192%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
193%%%%%%%%%%%%%%%%%%%
194a_average=zeros(1,rr); %Array for saving the
195best (a) values for rr times
196Rs_average=zeros(1,rr); %Array for saving the best
197(Rs) values for rr times
198Rp_average=zeros(1,rr); %Array for saving the
199best (Rp) values for rr times
200Iph_average=zeros(1,rr); %Array for saving
201the best (Iph) values for rr times
202Io_average=zeros(1,rr); %Array for saving the best
203(Io) values for rr times
204f_average=zeros(1,rr); %Array for saving the
205best (f) values for rr times
206for b=1:rr %Repeat the algorithm 10
207times
208%%%%%%%%//// Algorithm's variables and matrices
209declaration
210////%%%%%%%
211x=zeros(D,1); %Trial vector
212pop=zeros(D,Np); %Population matrix (target
213matrix)
214Fit=zeros(1,Np); %Overall fitness function
215matrix of the population
216r=zeros(3,1); %Randomly selected indices
217for mutation stage
218%%%%%%%%%%%%%%%%%//// Initializing the population
219////%%%%%%%%%%%%%%%%%
220for j=1:Np %For all individuals
221vector
222for i=1:D %For all variables of
223individual vector
224pop(i,j)=L(i)+(H(i)-L(i))*rand(1,1);
225%Initializing the individuals vector
226end
227a=pop(1,j); %Specified the diode
228ideality factor value from population
229Rs=pop(2,j); %Specified the PV series
230resistance value from population
231Rp=pop(3,j); %Specified the PV parallel
232resistance value from population
233Iph=pop(4,j); %Specified the photo
234current value from population
235Io=pop(5,j); %Specified the diode
236saturation current value from population
237[ f]=fitness_function(a,Rs,Rp, Iph,Io,G,Tc); %Call
238the function of computing the fitness functions
239Fit(1,j)=f; %To save the overall fitness
240function for initial population
241end
242%%%%%%%%%%%%%%%%%%%%%%%%//// Optimization
243////%%%%%%%%%%%%%%%%%%%%%%%%%
244Aa=zeros(1,GEN_max); %Initialize array for
245(a) values
246ARs=zeros(1,GEN_max); %Initialize array
247for (Rs) values
248ARp=zeros(1,GEN_max); %Initialize array for
249(Rp) values
250AIph=zeros(1,GEN_max); %Initialize array
251for (Iph) values
252AIo=zeros(1,GEN_max); %Initialize array for
253(Io) values
254Af=zeros(1,GEN_max); %Initialize array for (f)
255values
256for g=1:GEN_max %For each generation
257(iteration)
258for j=1:Np %For each individual
259vector
260%%%%//// Selection three randomly indices for
261mutation ////%%%%
262%%%%%%%//// step to generate donor (mutation)
263vector ////%%%%%%
264r(1)=floor(rand*Np)+1; %First random
265index
266while r(1)==j %To ensure . . .
267r(1)=floor(rand*Np)+1; %r(1)not equal j
268end
269r(2)=floor(rand*Np)+1; %Second random
270index
271while (r(2)==j)||(r(2)==r(1)) %To ensure . . .
272r(2)=floor(rand*Np)+1; %r(2)not equal
273j and r(1)
274end
275r(3)=floor(rand*Np)+1; %Third random
276index
277while (r(3)==j)||(r(3)==r(1))||(r(3)==r(2))
278%To ensure . . .
279r(3)=floor(rand*Np)+1; %r(1)not equal
280j and r(1)and r(2)
281end
282%%%%%%%%%%%%%%%%%%%//// Mutation steps
283////%%%%%%%%%%%%%%%%%%%%
284w=pop(:,r(3))+F.*(pop(:,r(1))-pop(:,r(2)));
285%To create the mutation (donor) vector
286%%%%%%%%%%%%%%%%%%//// Crossover steps
287////%%%%%%%%%%%%%%%%%%%%
288Rnd=floor(rand*D)+1;
289for i=1:D
290if (rand<CR)||(Rnd==i)
291x(i)=w(i);
292else
293x(i)=pop(i,j);
294end
295end
296%%%%%//// Checking the 5-PV-parameters of trial
297vector ////%%%%
298%%%%%%%%%%%%//// with the boundary constraints
299////%%%%%%%%%%%%
300for i=1:D
301if (x(i)<L(i))||(x(i)>H(i))
302x(i)=L(i)+(H(i)-L(i))*rand;
303end
304end
305%%%%%%//// Selection the best individual
306(either the ////%%%%%%
307%%%%%%%%%%%//// trial or current individual
308vector)////%%%%%%%%
309a=x(1); %Specified the diode ideality
310factor value trial vector
311Rs=x(2); %Specified the PV series
312resistance value trial vector
313Rp=x(3); %Specified the PV parallel
314resistance value trial vector
315Iph=x(4); %Specified the photo current
316value trial vector
317Io=x(5); %Specified the diode saturation
318current value trial vector
319[f]=fitness_function(a,Rs,Rp,Iph,Io,G,Tc);
320%Calculate the fitness functions for trial vector
321if (f<=Fit(1,j)) %Comparison between fitness
322functions for trial and target vectors
323pop(:,j)=x; %Replace the target individual
324by trial individual vector
325Fit(1,j)=f; %Replace the overall fitness
326function (f.f) of target individual vector with the
327fitness
328function of trial one
329end
330end %End the loop for each
331individual vectors
332[n iBest]=min(abs(Fit));
333Aa(g)= pop(1,iBest); %To save the best value of
334(a) for each generation
335ARs(g)=pop(2,iBest); %To save the best value
336of (Rs) for each generation
337ARp(g)=pop(3,iBest); %To save the best value of
338(Rp) for each generation
339AIph(g)=pop(4,iBest); %To save the best value
340of (Iph) for each generation
341AIo(g)=pop(5,iBest); %To save the best value of
342(Io) for each generation
343Af(g)=Fit(iBest); %To save the value of f
344if Fit(iBest)<=EP
345FEV=g;
346end
347end %End the loop for each generation
348(iteration)
349[nn Ibest]=min(abs(Af));
350a_average(b)=Aa(1,Ibest);
351Rs_average(b)=ARs(1,Ibest);
352Rp_average(b)=ARp(1,Ibest);
353Iph_average(b)=AIph(1,Ibest);
354Io_average(b)=AIo(1,Ibest);
355f_average(b)=Af(1,Ibest);
356AF=Af';
357xlswrite ('PVM4_Try_3.xlsx',AF,sheet,'Z5');
358end
359%%%%%%//// Results of optimization of 3-parameters of PV
360module ////%%%%%%%
361f_bestt=sum(f_average)/rr; %The overall fitness
362function of the best individual
363a_bestt=sum(a_average)/rr; %The best value of (a) for
364each solar radiation and ambient temperature
365Rs_bestt=sum(Rs_average)/rr; %The best value of (Rs)
366for each solar radiation and ambient temperature
367Rp_bestt=sum(Rp_average)/rr; %The best value of (Rp)
368for each solar radiation and ambient temperature
369Iph_bestt=sum(Iph_average)/rr; %The best value of (Iph)
370for each solar radiation and ambient temperature
371Io_bestt=sum(Io_average)/rr; %The best value of (Io)
372for each solar radiation and ambient temperature
373save(file_name,'f_average'); %To save the fitness
374function in MAT file for rr run
375xlswrite ('PVM4_Try_3.xlsx',f_average,sheet,'A108');
376%To save the fitness function in excel sheet for rr run
377%%%% MATLAB Script function for computing the fitness
378functions of %%%% Differential Evolution (DE)algorithm
379%%%% for optimizing the 5-PV-parameters (a, Rs, Rp, Iph & Io)
380%%%% Date 16/5/2015 - Monday
381function [f]=fitness_function(a,Rs,Rp,Iph,Io,G,Tc)
382%%Define a function to compute the fitness functions
383%%%%%%%%%%%%%%%%%//// Declaration the constants
384////%%%%%%%%%%%%%%%%%%%%%%%
385Nsc=36; %Number of cells are connected in
386series per module
387k=1.3806503*10^-23; %Boltzmann constant (J/K)
388q=1.60217646*10^-19; %Electron charge in (Coulomb)
389VT=(Nsc*k*Tc)/q; %Diode thermal voltage (v)
390%%%%%%%%//// Reading the experimental voltage and current
391data ////%%%%%%%%
392%Vp=xlsread('Datamodified.xlsx',1,'AA3:AA104');
393%Ie=xlsread('Datamodified.xlsx',1,'AB3:AB104');
394load ('var_fitness_function', 'Vp','Ie');
395%%%%%%%%%%%%%%%%//// Computing the theoretical current
396////%%%%%%%%%%%%%%%%
397Ip=zeros(size(Vp));
398for h=1:5
399Ip=Ip ‐ ((Iph‐Ip‐Io.*(exp((Vp+Ip.*Rs)./(a.*VT))‐1)‐…
400((Vp+Ip.*Rs)./Rp))./(‐1‐Io.*(Rs./(a.*VT)).* …
401exp((Vp+Ip.*Rs)./(a.*VT))-(Rs./Rp)));
402end
403%%%%%%%%%%%%%%%%%//// Computing the fitness function
404////%%%%%%%%%%%%%%%%%%
405N=length(Vp);
406f=sqrt((1/N)*sum((Ie-Ip).^2));
407%MATLAB script to plot the and experimental I-V and P-V
408characteristicsنتایج اجرای برنامه نوشته شده، شکلهای زیر خواهد بود.