محاسبه خطای مدل با پایتون — راهنمای گام به گام

امروزه به منظور انتخاب مدل با کمترین متغیرها و جلوگیری از بیش‌برازش یا کم‌برازش از ابزاری به نام «اعتبار سنجی متقابل» (Cross Validation) استفاده می‌شود. به این ترتیب مدلی مناسب است که توسط اعتبار سنجی متقابل، خطا یا واریانس آن برآورد شده باشد و دارای کمترین خطا نسبت به دیگر مدل‌های مشابه باشد. در این نوشتار با استفاده از کتابخانه‌های موجود در پایتون به بررسی و پیاده‌سازی اعتبار سنجی متقابل خواهیم پرداخت. در این بین از کتابخانه‌های pandas ،sklearn ،matplotlib استفاده خواهیم کرد و در پی محاسبه خطای مدل با پایتون خواهیم بود.

برای آشنایی بیشتر با نحوه عملکرد اعتبار سنجی متقابل، مطلب اعتبار سنجی متقابل (Cross Validation) — به زبان ساده را مطالعه کنید. همچنین خواندن نوشتار بیش برازش (Overfitting)، کم برازش (Underfitting) و برازش مناسب — مفهوم و شناسایی نیز خالی از لطف نیست.

محاسبه خطای مدل در پایتون

همانطور که می‌دانید، با افزایش تعداد متغیرها، خطای مدل برای داده‌هایی موجود کاهش می‌یابد ولی اگر مدل حاصل را بر روی داده‌هایی دیگری به کار ببریم، ممکن است خطای مدل غیرقابل جبران باشد. این مشکل را به نام «بیش‌برازش» (Overfitting) می‌شناسیم. بنابراین به نظر می‌رسد که مبنای اندازه‌گیری خطای مدل براساس داده‌هایی که مدل را ایجاد کرده‌اند، کاری اشتباه است. به این منظور باید خطای مدل‌های مختلف را براساس داده‌هایی که در ایجاد این مدل‌ها نقشی نداشته‌اند، محاسبه کرد، سپس به انتخاب مدل مناسب درست زد.

فیلم آموزش برنامه نویسی پایتون ویژه نوجوانان – بخش یکم در فرادرس

کلیک کنید

دو مفهوم و ابزار مهم در «علم داده» (Data Science) به منظور جلوگیری یا کاهش اثرات بیش‌برازش وجود دارد. اولین ابزار براساس تفکیک داده‌ها به دو بخش آموزشی و آزمایشی (Train/Test Split) عمل می‌کند و دومین روش نیز «اعتبار سنجی متقابل» (Cross Validation) نامیده می‌شود.

محاسبه خطای مدل به روش تفکیک آموزشی/آزمایشی داده‌ها

همانطور که قبلا اشاره کردیم، در روش تفکیک آموزشی/آزمایشی، داده‌های جمع‌آوری شده به دو بخش تقسیم می‌شوند. بخش اول از داده‌ها به منظور برآورد پارامترهای مدل استفاده می‌شود. این برآورد به شکلی است که خطای مدل حاصل براساس داده‌های آموزشی، حداقل مقدار را خواهد داشت. ولی در بخش بعدی، داده‌های آزمایشی به منظور اندازه‌گیری خطای مدل به کار رفته و مقدارهای پیش‌بینی شده طبق مدل محاسبه می‌شوند.

براساس فاصله‌ای که مقدار واقعی و پیش‌بینی شده توسط مدل برای داده‌های آزمایشی دارد، خطای مدل برآورد می‌شود. در بین مدل‌هایی که با تعداد متغیرهای مختلف ایجاد شده و با داده‌های آزمایشی مورد بررسی قرار گرفته‌اند، مدلی که دارای کمترین خطای آزمایشی باشد، مدل مناسب تشخیص داده می‌شود.

در این قسمت با استفاده پایتون و کتابخانه Scikit-Learn و روش train_test_split این روش را به کار می‌بریم. ابتدا کتابخانه‌ها را نصب و راه‌اندازی می‌کنیم و سپس به معرفی این کتابخانه‌ها می‌پردازیم.

1import pandas as pd
2from sklearn import datasets, linear_model
3from sklearn.model_selection import train_test_split
4from matplotlib import pyplot as plt

کتابخانه Pandas: از این کتابخانه به منظور فراخوانی فایل‌های داده و تحلیل آن‌ها استفاده خواهیم کرد.

کتابخانه Sklearn: در این متن، برای ایجاد رگرسیون و مدل خطی از کتابخانه Sklearn و زیر کتابخانه model_selection استفاده شده است. همچنین با استفاده از datasets به مجموعه‌ای از داده‌های موجود در این کتابخانه دسترسی خواهیم داشت. با انتخاب train_test_split نیز به امکان تفکیک داده‌ها به دو بخش آموزشی و آزمایشی بوجود می‌آید.

کتابخانه Matplotlib: از کتابخانه Matplotlib دستور $$pyplot$$ را به منظور ترسیم نمودارهای مربوط به داده‌ها به کار گرفته‌ایم.

حال براساس «مجموعه داده‌ دیابت» (diabetes dataset) دست به ایجاد مدل می‌زنیم. ولی باید ابتدا داده‌ها را در یک چارچوب داده، قرار داده و متغیرها را نام‌گذاری کنیم. این کار در کد زیر صورت گرفته است.

1# Load the Diabetes Housing dataset
2columns = “age sex bmi map tc ldl hdl tch ltg glu”.split() # Declare the columns names
3diabetes = datasets.load_diabetes() # Call the diabetes dataset from sklearn
4df = pd.DataFrame(diabetes.data, columns=columns) # load the dataset as a pandas data frame
5y = diabetes.target # define the target variable (dependent variable) as y

به این ترتیب مجموعه داده به نام df ساخته شده و متغیر y نیز به عنوان متغیر پاسخ یا وابسته (Dependent Variable) از ستون target داده‌های diabetes معرفی شده است.

حال با استفاده از تابع train_test_split عمل تفکیک داده‌ها را انجام می‌دهیم. در اینجا ۲۰٪ داده‌ها را برای بخش آزمایش در نظر گرفته‌ایم. معمولا نسبت داده‌های آموزشی به آزمایشی به صورت ۸۰ به ۲۰ یا ۳۰ به ۷۰ در نظر گرفته می‌شود. یعنی برای مثال ۸۰ درصد داده‌ها برای مدل‌سازی و ۲۰ درصد باقی‌مانده برای برآورد خطای مدل به کار می‌رود.

1# create training and testing vars
2X_train, X_test, y_train, y_test = train_test_split(df, y, test_size=0.2)
3print X_train.shape, y_train.shape
4print X_test.shape, y_test.shape
5(353, 10) (353,)
6(89, 10) (89,)

خروجی اجرای این دستورات در دو سطر آخر دیده می‌شود. بنابراین 353 مشاهده ( با ۱۰ متغیر مستقل) به عنوان متغیر X_train و به همین تعداد نیز به عنوان متغیر وابسته در Y_train ثبت می‌شود. همچنین ۸۹ مشاهده نیز برای بخش آزمایش در نظر گرفته شده است.

به کمک دستورات زیر مدل مناسب برای داده‌های آموزشی را تشکیل می‌دهیم. همانطور که مشخص است متغیر X_train به عنوان متغیر مستقل و متغیر y_train به عنوان متغیر وابسته در مدل نقش دارند. نتیجه برآورد مدل در متغیر model و مقدارهای پیش‌بینی شده برای مشاهدات توسط مدل نیز در متغیر predictions ثبت شده‌اند.

1# fit a model
2lm = linear_model.LinearRegression()
3model = lm.fit(X_train, y_train)
4predictions = lm.predict(X_test)

در ادامه مقدارهای پیش بینی شده برای پنچ مشاهده اول را می‌بینید.

1predictions[0:5]
2array([ 205.68012533,   64.58785513,  175.12880278,  169.95993301,
3        128.92035866])

نکته: اندیس‌ها در پایتون از صفر شروع می‌شود. همچنین اندیس دوم یعنی 5 نیز در دستور $$predictions[0:5]$$ به این معنی است که مشاهدات باید تا اندیس قبل از ۵ نمایش داده شوند.

حال به بررسی مدل بوسیله رسم و مقایسه مقدارهای واقعی (True values) و پیش‌بینی شده (Predictions) می‌پردازیم. کد زیر به این منظور تهیه شده است.

1## The line / model
2plt.scatter(y_test, predictions)
3plt.xlabel(“True Values”)
4plt.ylabel(“Predictions”)

خروجی این دستورات، نموداری است که انتظار داریم نقاط رسم شده در آن نزدیک به یک خط نیمساز ربع اول باشد.

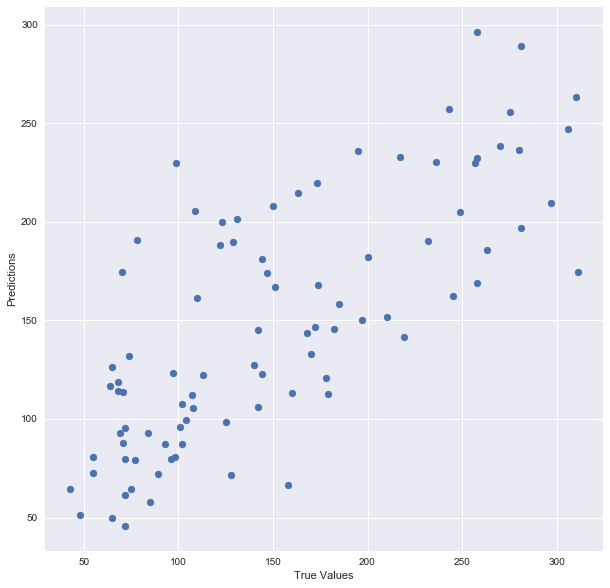
برای اندازه‌گیری دقت مدل نیز از تابع model.score استفاده خواهیم کرد. به این ترتیب مشخص است که دقت این مدل حدود ۵۰٪ است.

1print “Score:”, model.score(X_test, y_test)
2Score: 0.485829586737

مقدار Score نشان می‌دهد که استفاده از ده متغیر (age, sex, bmi, map, tc, ldl, hdl, tch, ltg, glu) دارای خطای تقریبا برابر با ۵۰٪ است.

از آنجایی که در روش تفکیک، ممکن است نمونه تصادفی گرفته شده دارای اریبی یا سوگیری باشد، بهتر است عمل نمونه‌گیری و تفکیک را در چند مرحله انجام داد. چنین حالتی را به عنوان اعتبار سنجی متقابل می‌شناسیم.

محاسبه خطای مدل با استفاده از روش اعتبار سنجی متقابل

این روش بسیار شبیه به روش تفکیک آموزشی/آزمایشی داده‌ها است. در واقع براساس چندین بار نمونه‌گیری و تغییر مجموعه آموزشی و آزمایشی، اثر خطای نمونه‌گیری در مدل تفکیکی از بین می‌رود. البته تعداد تکرار و تعداد اندازه‌ مجموعه‌های اعتبار سنجی از نکاتی است که در این روش باید مد نظر قرار گیرد.

فیلم آموزش پروژه محور جنگو و پایتون – طراحی سایت و وب اپلیکیشن با فریمورک Django در فرادرس

کلیک کنید

در این روش مجموعه داده‌های آموزشی خود به بخش‌هایی به نام بخش‌های اعتبار سنجی تقسیم می‌شود و هر بار براساس یکی از این مجموعه‌ها مدل برازش شده و در انتها نیز بهترین مدل براساس میانگین کمترین میزان خطای آموزشی انتخاب می‌شود. در انتها نیز برآورد خطای مدل براساس داده‌های آزمایشی صورت گرفته و خطای مدل حاصل از اعتبار سنجی متقابل، اندازه‌گیری می‌شود.

هر چند شیوه‌های مختلفی در اجرای اعتبار سنجی متقابل وجود دارد ولی در اینجا به دو شیوه «k-Fold» و «Leave-One-Out» یا «LOOCV» می‌پردازیم.

اعتبار سنجی متقابل K-Folds

در این حالت، داده‌ها به k زیر قسمت یا fold طبقه‌بندی می‌شوند. یکی از این قسمت‌ها جدا شده و براساس بقیه داده‌های مدل برازش می‌شود. خطای مدل به کمک قسمت جدا شده اندازه‌گیری می‌شود. این کار تکرار شده تا همه قسمت‌ها یا foldها در اندازه‌گیری خطا‌ها به کار روند. میانگین خطاهای حاصل، برآورد خطای مدل خواهد بود. در انتها نیز مدل براساس داده‌های آزمایشی سنجش می‌شود.

همانطور که دیده می‌شود، تصویر زیر عملکرد این روش را به روشنی مشخص می‌کند.

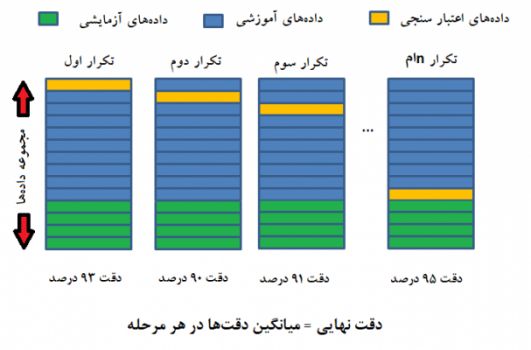
حال در اینجا به یک مثال در این زمینه می‌پردازیم. کد زیر یک بردار ایجاد کرده و عمل تقسیم‌بندی و ایجاد foldها را انجام می‌دهد. تابع اصلی در این کد KFold است.

1from sklearn.model_selection import KFold # import KFold
2X = np.array([[1, 2], [3, 4], [1, 2], [3, 4]]) # create an array
3y = np.array([1, 2, 3, 4]) # Create another array
4kf = KFold(n_splits=2) # Define the split - into 2 folds 
5kf.get_n_splits(X) # returns the number of splitting iterations in the cross-validator
6print(kf) 
7KFold(n_splits=2, random_state=None, shuffle=False)

در این مثال داده‌های آموزشی به دو بخش یا fold تفکیک شده‌اند. در نتیجه تعداد تکرارها نیز برابر با ۲ است. با اجرای دستورات زیر بخش‌های آموزشی و اعتبارسنجی در هر سطر دیده می‌شوند.

1for train_index, test_index in kf.split(X):
2 print(“TRAIN:”, train_index, “TEST:”, test_index)
3 X_train, X_test = X[train_index], X[test_index]
4 y_train, y_test = y[train_index], y[test_index]
5('TRAIN:', array([2, 3]), 'TEST:', array([0, 1]))
6('TRAIN:', array([0, 1]), 'TEST:', array([2, 3]))

اعتبار سنجی متقابل Leave-One-Out

در این روش، تعداد بخش‌ها برابر با تعداد مشاهدات است. به این ترتیب در هر بار یک مشاهده از داده‌های آموزش کنار گذاشته شده و مدل براساس بقیه ساخته می‌شود. سپس خطای مقداری که کنار گذاشته شده اندازه‌گیری می‌شود. با تکرار این عمل برای همه مشاهدات میانگین خطای حاصل، برآوردی برای خطای مدل خواهد بود. کد زیر به منظور اجرای اعتبار سنجی متقابل Leave-One-Out تهیه شده است.

1from sklearn.model_selection import LeaveOneOut 
2X = np.array([[1, 2], [3, 4]])
3y = np.array([1, 2])
4loo = LeaveOneOut()
5loo.get_n_splits(X)
6
7
8for train_index, test_index in loo.split(X):
9   print("TRAIN:", train_index, "TEST:", test_index)
10   X_train, X_test = X[train_index], X[test_index]
11   y_train, y_test = y[train_index], y[test_index]
12   print(X_train, X_test, y_train, y_test)

خروجی این دستورات، گروه‌های مربوط به این روش را تولید می‌کند. همانطور که در ادامه دیده می‌شود، تفاوت مرحله اول و دوم در قرارگیری بردارها است. در مرحله دوم جای مجموعه آموزشی یا اعتبار سنجی نسبت به مرحله اول تغییر کرده است.

1('TRAIN:', array([1]), 'TEST:', array([0]))
2(array([[3, 4]]), array([[1, 2]]), array([2]), array([1]))
3('TRAIN:', array([0]), 'TEST:', array([1]))
4(array([[1, 2]]), array([[3, 4]]), array([1]), array([2]))

اگر داده‌های موجود در بخش آموزش زیاد باشند، زمان و هزینه محاسباتی این روش زیاد است. بنابراین در چنین مواقعی از روش K-Fold استفاده می‌شود.

حال به بررسی مثال اولیه برمبنای اعتبار سنجی متقابل می‌پردازیم. در اینجا با استفاده از تابع $$cross_val_predict$$ مقدارهای برآورده شده محاسبه شده و در بخش آزمایش به کار می‌روند. ابتدا بارگذاری کتابخانه‌های مورد نیاز را انجام می‌دهیم.

1# Necessary imports: 
2from sklearn.cross_validation import cross_val_score, cross_val_predict
3from sklearn import metrics

همانطور که به یاد دارید داده‌ها مربوط به بیماران دیابتی بود. در اینجا اعتبار سنجی متقابل را با تعداد بخش‌ها Fold=6 انجام می‌دهیم.

1# Perform 6-fold cross validation
2scores = cross_val_score(model, df, y, cv=6)
3print “Cross-validated scores:”, scores
4Cross-validated scores: [ 0.4554861   0.46138572  0.40094084  0.55220736  0.43942775  0.56923406]

هر یک از امتیازات بدست آمده، مربوط به میزان دقت مدل‌هایی است که توسط یکی از شش بخش ایجاد شده است.

حال به بررسی برآوردهای جدید براساس اعتبار سنجی متقابل می‌پردازیم. کد زیر به این منظور تهیه شده است.

1# Make cross validated predictions
2predictions = cross_val_predict(model, df, y, cv=6)
3plt.scatter(y, predictions)

خروجی نموداری است که نسبت به نمودار اولیه شش برابر نقطه بیشتر دارد زیرا در اینجا شش مدل در کنار یکدیگر ترسیم شده‌اند.

حال برای نشان دادن میزان دقت از معیار $$R^2$$ کمک می‌گیریم. کد زیر به منظور محاسبه این ضریب به نوشته شده است.

1accuracy = metrics.r2_score(y, predictions)
2print “Cross-Predicted Accuracy:”, accuracy
3Cross-Predicted Accuracy: 0.490806583864

اگر مطلب بالا برای شما مفید بوده است و علاقه‌مند به یادگیری بیشتر در این زمینه هستید، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش های داده کاوی یا Data Mining در متلب
• مجموعه آموزش‌های یادگیری ماشین و بازشناسی الگو
• آموزش تخمین خطای طبقه بندی یا Classifier Error Estimation
• بیش برازش (Overfitting)، کم برازش (Underfitting) و برازش مناسب — مفهوم و شناسایی
• اعتبار سنجی متقابل (Cross Validation) — به زبان ساده

^^