جذر چیست؟ – محاسبه رادیکال به زبان ساده
اغلب با محاسبات چهار عمل اصلی آشنایی داریم. میدانیم که جمع به معنی افزایش مقدار به تعداد واحدی است که مشخص کردهایم. تفاضل به معنی کاهش مقدار به تعداد واحدی است که تعیین شده. همینطور ضرب و تقسیم نیز به صورتی با عمل جمع ارتباط دارند. به این معنی که میتوان ضرب را جمع یک عدد مثل a به تعداد r بار در نظر گرفت. به این ترتیب که در اینجا عمل جمع r بار تکرار شده است.


به هر حال مشخص است که دانش بشر براساس تجربیاتش پایهریزی شده و تجربه جمع کردن اعداد که برایش لذتبخش بوده باعث شده است تا آن را توسعه داده، چهار عمل اصلی و همینطور محاسبات پیچیدهتر مانند توان و لگاریتم را ابداع کند. به این ترتیب حساب و علوم مرتبط با ریاضیات، مثل هندسه و فیزیک گسترش یافته و هر روز جنبههای جدیدی به دانستهها و ابداعات انسان افزوده میشود. محاسبه ریشه دوم اعداد نیز یکی از ابتکاراتی است که گستردگی دامنه دانش انسان در محاسبات و کار بر روی اعداد را نشان میدهد.
در این نوشتار از مجله فرادرس سعی داریم با ریشه دوم و شیوه محاسبه آن آشنا شویم. البته محاسبه ریشه دوم یک عدد با ماشین حساب یا نرمافزارهای رایانهای کاری ساده محسوب میشود ولی میخواهیم از روش محاسبه آن بدون هیچ ابزاری آگاه شویم. ابتدا روش هندسی، سپس روش محاسبات عددی و در انتها نیز روش تجزیه به عوامل اول را برای پیدا کردن ریشه دوم یک عدد شرح میدهیم. برای آشنایی با اعداد و شیوه حل تساویها و ناتساویها بهتر است ابتدا مطلب معادله و نامعادله در ریاضی — پیدایش و کاربردها از مجله فرادرس را مطالعه کنید. البته آشنایی با روش حل معادله درجه دو — به زبان ساده نیز خالی از لطف نیست.
ریشه دوم عدد و محاسبه آن
فرض کنید عددی مثبت باشد. ریشه دوم یا جذر این عدد نیز یک عدد است که آن را با نشان میدهیم.
نحوه ارتباط ریشه عدد با خود عدد در زیر دیده میشود.
این تساوی نشان میدهد که منظور از ریشه عدد عددی است که اگر به توان 2 برسد، عدد حاصل شود. برای مثال میدانیم که ریشه دوم عدد 4 برابر است با 2 زیرا:
از طرفی 2- نیز ریشه دوم عدد 4 است. به همین ترتیب میتوان نشان داد که ریشه دوم مثبت ۲۵ برابر با ۵ و 6- ریشه دوم ۳۶ است. چنین اعدادی که دارای ریشه با مقدار صحیح هستند، اعداد مربع کامل نامیده میشوند. جدول زیر بعضی از این اعداد را معرفی کرده است.
| عدد | |||||||||
| ریشه دوم |
ولی چگونه باید برای اعدادی که مربع کامل نیستند، ریشه دوم را محاسبه کرد. به این منظور دو روش هندسی و محاسباتی به همراه تجزیه به عوامل اول را معرفی میکنیم.
روش هندسی برای ریشه دوم عدد
حتما با قضیه فیثاغورس (فیثاغورث) آشنایی دارید. به هر حال برای یادآوری صورت این قضیه را در اینجا تکرار میکنیم. «در یک مثلث قائمالزاویه (سه گوش راست) مجموع مربعات دو ضلع مجاور به زاویه قائمه (راست) برابر با مربع ضلع دیگر یعنی وتر است. تصویر زیر این معادله را به خوبی نشان میدهد. ما نیز در اینجا برای محاسبه ریشه دوم یک عدد، دقیقا از همین خاصیت استفاده خواهیم کرد.
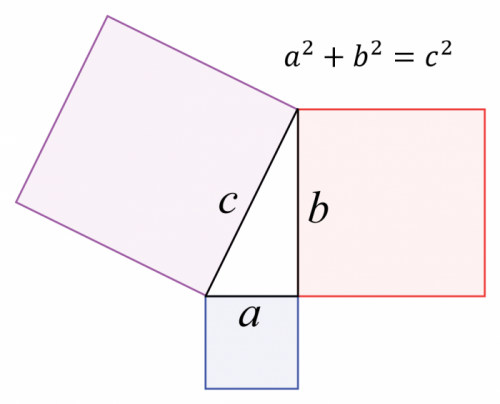
به این ترتیب از محور اعداد کمک میگیریم و برای مثلا عدد 5، ریشه دوم را محاسبه میکنیم. از آنجایی که نزدیکترین عدد مربع کامل به 5 عدد 4 است، روی محور اعداد ریشه دوم عدد 4 را مشخص میکنیم که برابر با 2 است. از محل قرارگیری 2 یک خط عمود بر محور به ارتفاع یک واحد ایجاد میکنیم. از نقطه مرکز محور اعداد (نقطه صفر) خطی به انتهای این نقطه وصل میکنیم. به این ترتیب یک مثلث قائمالزاویه ایجاد میشود. تصویر زیر این وضعیت را بهتر نشان میدهد.
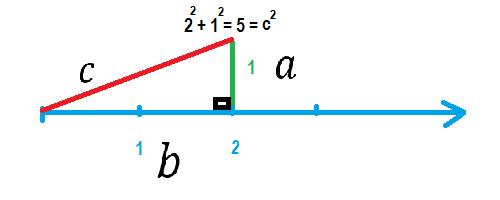
با توجه به شکل به راحتی میتوان دید که طول ضلع c همان ریشه دوم 5 است. برای نمایش این عدد روی محور اعداد، کمانی به طول c و مرکز صفر رسم میکنیم تا محور اعداد را قطع کند. محل برخورد، نشانگر عدد ، یعنی ریشه دوم 5 است.
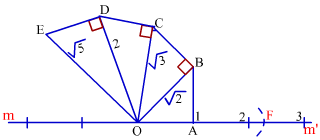
نکته: اگر بخواهیم مقدار را روی محور اعداد نشان دهیم، این بار طول ضلع b را برابر با و طول ضلع a را همان ۱ در نظر میگیریم. با محاسبه طول ضلع c در قضیه فیثاغورس و رسم کمان، روی محور اعداد مقدار نیز مشخص میشود. برای محاسبه ریشه دوم ۵ یعنی نیز میتوان عمل محاسبه را به طور متوالی برای سپس ، آنگاه انجام داد. تصویر زیر این مراحل را در روی محور اعداد نشان میدهد.
مثال
برای محاسبه ریشه دوم عدد ۱۰ به روش هندسی مراحل زیر را طی میکنیم.
- نزدیکترین عدد مربع کامل به ۱۰ مقدار ۹ با ریشه دوم برابر با ۳ است.
- روی محور اعداد طولی برابر با ۳ انتخاب میکنیم.
- به ارتفاع ۱ واحد خطی عمود بر محور اعداد ترسیم میکنیم.
- یک خط از مرکز محور (نقطه صفر) به انتهای این خط میکشیم.
- برابر با طول این خط روی محور اعداد جدا میکنیم تا ریشه دوم عدد ۱۰ را نشان دهد.
نکته: برای جدا کردن این طول روی محور اعداد میتوانید از پرگار استفاده کنید. کافی است سوزن پرگار را روی نقطه صفر قرار داده و سر دیگر را در انتهای خط ایجاد شده در مرحله ۴ قرار دهید. سپس یک کمان رسم کنید تا محور اعداد را قطع کند. طول خطی که از محل برخورد این کمان با محور تا مرکز ایجاد میشود، ریشه دوم ۱۰ را نشان میدهد.
مثال
برای محاسبه ریشه دوم عدد 13 بهتر است از مربع دو عدد ۳ و ۲ استفاده کنیم. زیرا . به این ترتیب روی محور اعداد مقدار ۳ را مشخص کرده و به ارتفاع ۲ واحد خطی عمود بر محور اعداد از این نقطه رسم میکنیم. طول خطی که مرکز مختصات را به انتهای این خط وصل میکند، مقدار ریشه دوم ۱۳ را نشان میدهد. کافی است براساس این طول، کمانی از مرکز محور اعداد (یعنی صفر) ترسیم کنیم تا محور را قطع کند. به این ترتیب ریشه دوم ۱۳ روی محور اعداد مشخص میشود.

مثال
برای پیدا کردن ریشه دوم عدد ۱۱ چه باید کرد؟ این کار نیز بسیار ساده است. بهتر است از مربع دو عدد و استفاده کنیم. زیرا . بنابراین کافی است ابتدا ریشه دوم عدد 2 را روی محور طولها بدست آورده، سپس به ارتفاع ۳ واحد خطی عمود بر محور در این نقطه ترسیم کنیم. سپس از محور مختصات تا انتهای این خط، خط دیگری ترسیم کنید. طول خط ترسیم شده مقدار ریشه دوم ۱۱ را نشان میدهد.
روش محاسباتی ریشه یک عدد براساس الگوریتم تکراری
به منظور محاسبه ریشه دوم یک عدد میتوان از الگوریتم زیر کمک گرفت. این الگوریتم برمبنای ریشهیابی معادله به کمک روش عددی نیوتن-رافسون عمل میکند.
به این ترتیب مراحل اجرای الگوریتم را میتوان به صورت زیر نوشت:
- انتخاب یک حدس اولیه به عنوان مقدار تقریبی ریشه دوم عدد
- محاسبه تقسیم عدد بر ریشه تقریبی آن
- محاسبه حاصل جمع مقدار ریشه تقریبی با مقدار حاصل از مرحله ۲
- بدست آوردن نصف مقدار حاصل از مرحله ۳
- تکرار الگوریتم از مرحله دوم با قرار دادن مقدار ریشه تقریبی از مرحله ۴
نکته: هر چه حدس اولیه یعنی به ریشه واقعی نزدیکتر باشد، سرعت همگرایی الگوریتم بیشتر خواهد شد. از طرفی هر چه تعداد تکرار این الگوریتم بیشتر باشد، محاسبه ریشه دوم عدد با دقت بیشتری صورت خواهد گرفت.
مثال
در اینجا سعی میکنیم ریشه دوم عدد ۲ را بدست آوریم. برای این کار مراحل الگوریتم را طی میکنیم.
- حدس اولیه برای ریشه دوم عدد ۲ را مقدار ۱ در نظر میگیریم.
- محاسبه
- محاسبه گام سوم الگوریتم یعنی
- نصف کردن نتیجه حاصل
- در نظر گرفتن مقدار به عنوان تقریب برای ریشه دوم عدد ۲ و تکرار الگوریتم از مرحله دوم
نتایج حاصل شده در محاسبه این تکرارها در جدول زیر ارائه شده است.
| تکرار | گام ۱ | گام ۲ | گام ۳ | گام ۴ | گام ۵ |
| ۱ | 1.000 | 2.000 | 3.000 | 1.500 | 1.500 |
| 2 | 1.500 | 1.333 | 2.833 | 1.4166 | 1.416 |
| 3 | 1.416 | 1.412 | 2.828 | 1.414 | 1.414 |
| 4 | 1.414 | 1.414 | 2.828 | 1.414 | 1.414 |
همانطور که مشخص است به سرعت این الگوریتم به همگرایی رسیده و بعد از طی چهار مرحله، پاسخها یکسان خواهند بود. بنابراین مقدار 1.414 ریشه دوم عدد ۲ است.
مثال
ریشه دوم عدد ۱۰ را به وسیله الگوریتم نیوتن-رافسون و تکرار عملیات مشابه جدول بالا، محاسبه میکنیم. در اینجا حدس اولیه را مقدار ۳ در نظر میگیریم که به مقدار ریشه ۱۰ نیز نزدیک است.
| تکرار | گام ۱ | گام ۲ | گام ۳ | گام ۴ | گام ۵ |
| ۱ | 3.000 | 3.333 | 6.333 | 3.166 | 3.166 |
| 2 | 3.166 | 3.158 | 6.325 | 3.162 | 3.162 |
| 3 | 3.162 | 6.325 | 3.162 | 3.162 | 3.162 |
باز هم دیده میشود که الگوریتم در گام سوم به همگرایی رسیده و ریشه عدد ۱۰ با تقریب سه رقم اعشار برابر با 3.162 است.
اگر میخواهید بیشتر با نحوه اجرای الگوریتم و محاسبات آن آشنا شوید، میتوانید از اینجا فایل اکسل مربوط به محاسبه ریشه دوم یک عدد را دریافت کنید. در این فایل محاسبات با دریافت عدد مورد نظر به همراه حدس اولیه آغاز شده و با طی کردن ۹ تکرار از الگوریتم به مقدار تقریبی برای ریشه عدد مورد نظر میرسد. این مقدار را در آخرین سلول مرحله ۹ قابل مشاهده است. بهتر است این مقدار را با محاسبه ریشه دوم عدد که با رنگ نارنجی در بالای کاربرگ قرار گرفته است مقایسه کنید تا دقت ریشهیابی الگوریتم را مشاهده کنید.

ارتباط الگوریتم با روش نیوتن-رافسون (Newton–Raphson Method)
اگر نمودار تابع را در نظر بگیریم، میتوان ریشه مقدار x را همان a در نظر گرفت. شکل این نمودار برای مقدار در تصویر زیر دیده میشود. همانطور که میدانید، یکی از روشهای عددی برای پیدا کردن ریشه یک معادله، روش «نیوتن-رافسون» (Newton-Rapson) نام دارد که براساس مشتق تابع عمل میکند. طبق این روش که به صورت یک الگوریتم تکراری است، میتوان ریشه یک معادله را براساس رابطه زیر به صورت عددی و تقریب مناسب بدست آورد.
مشخص است که در اینجا شماره مرحله اجرای الگوریتم است. در این رابطه منظور از یک حدس اولیه برای ریشه است که الگوریتم با آن آغاز میشود. مقدار تابع در نقطه و همچنین مشتق تابع در نقطه را نشان میدهد که برابر با است. به این ترتیب با طی چند مرحله میتوان به جواب معادله رسید که برابر با ریشه دوم مقدار a است.
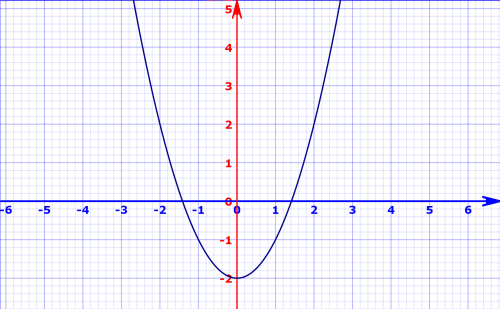
حال این الگوریتم را با الگوریتمی که در قسمت قبلی برای محاسبه ریشه دوم عدد معرفی کردیم، مقایسه میکنیم. فرض کنید که قرار است ریشه دوم عدد a را محاسبه کنیم.
به این ترتیب مشخص میشود که برای پیدا کردن ریشه دوم یک عدد براساس مقدار تقریبی میتوان همان الگوریتم بالا را به کار برد. به این معنی که ابتدا عدد را به حدس اولیه یا تقریب ریشه تقسیم کرد. سپس با مقدار حدس یا تقریب ریشه جمع و در انتها نیز نسبت نتیجه حاصل را بر ۲ بدست آورد.
روش تجزیه به عوامل اول
یک راه حل دیگر برای محاسبه ریشه دوم یک عدد، استفاده از تجزیه آن به عوامل اول است. برای آشنایی بیشتر با اعداد اول میتوانید به مطلب اعداد اول — به زبان ساده مراجعه کنید. به این ترتیب تجزیه یک عدد به عوامل اول به معنی نمایش آن عدد برحسب حاصلضرب اعداد اولی است که آن را میسازند.
برای محاسبه ریشه دوم (یا حتی ریشههای سوم و بیشتر) میتوان از روش تجزیه به عوامل اول استفاده کرد. ولی باید توجه داشت که این روش، زمانی مناسب است که عدد مورد نظر بزرگ (مثلا بزرگتر از ۱۰) باشد و بتوان آن را به عوامل اول تجزیه نمود. بنابراین برای محاسبه ریشه دوم اعداد اول (مثل ۲، ۳ و ۵) این روش مناسب نیست.

نکته: برای محاسبه ریشه براساس تجزیه به عوامل اول، باید عدد مورد نظر حتما صحیح باشد تا بتوان آن را به عوامل اول تجزیه کرد. در غیراینصورت، امکان استفاده از این روش وجود ندارد و باید براساس روش تقریبی و الگوریتم تکراری نیوتن رافسون محاسبات را انجام داد.
منظور از تجزیه یک عدد مثل به عوامل اول، نوشتن آن به صورت حاصلضرب اعداد اول است. برای مثال میتوان 12 را به صورت ضرب عوامل اول به صورت زیر نشان داد.
درنتیجه ریشه دوم عدد ۱۲ را میتوان مطابق با محاسبات زیر بدست آورد.
بنابراین برای محاسبه ریشه دوم ۱۲ فقط کافی است که ریشه دوم ۳ را داشته باشیم تا دو برابر آن را به عنوان ریشه دوم عدد ۱۲ محسوب کنیم. البته مشخص است که برای بدست آوردن ریشه دوم عدد ۳ میتوان از الگوریتمی که در بالا به آن اشاره شد، استفاده کرد.
تجزیه به عوامل اول
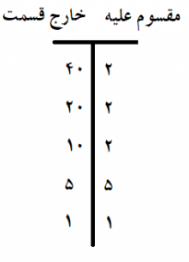
برای تجزیه یک عدد مثل به عوامل اول، ابتدا آن را به کوچکترین عدد اولی که به آن بخشپذیر است، تقسیم میکنیم. همین کار را برای خارج قسمت این تقسیم نیز انجام میدهیم. این کار را تا زمانی که خارج قسمت ۱ شود (و باقی مانده تقسیم صفر) ادامه میدهیم. حال با ضرب اعداد اول که به عنوان مقسوم علیه به کار بردهاید، عدد ساخته میشود به این ترتیب، توانستیم را به صورت ضرب عاملهای اول بنویسیم.
برای مثال فرض کنید میخواهیم عدد ۴۰ را به عوامل اول تجزیه کنیم. کوچکترین عدد اولی که ۴۰ بر آن بخشپذیر است، عدد ۲ است. پس داریم:
مثال
ریشه دوم عدد 40 را به روش تجزیه به عوامل اول محاسبه میکنیم. براساس تجزیه عدد 40 داریم:
در نتیجه ریشه دوم عدد ۴۰ به صورت زیر در خواهد آمد.
بنابراین برای محاسبه ریشه دوم عدد ۴۰، باید ریشههای دوم عدد ۲ و ۵ را محاسبه کرده تا حاصلضرب آنها را دو برابر کرده و ریشه دوم ۴۰ را بدست آوریم.
مثال
ریشه دوم عدد 972 را به کمک روش تجزیه به عوامل اول بدست میآوریم. طبق تصویر زیر این عدد را به عوامل اول تجزیه کردهایم.

بنابراین میتوان این عدد را به صورت حاصلضرب عوامل اول نوشت:
که حاصل با در نظر گرفتن مقدار تقریبی برابر با خواهد بود.
برای محاسبه ریشه سوم و یا بالاتر نیز از این روش استفاده میشود. برای روشن شدن این مطلب فرض کنید که قرار است ریشه سوم عدد 256 را محاسبه کنیم. میدانیم که تجزیه این عدد به عوامل اول به صورت زیر خواهد بود.
بنابراین برای محاسبه ریشه سوم این عدد خواهیم داشت:
به نظر شما برای محاسبه ریشه سوم عدد ۴ چگونه باید عمل کرد. برای آگاهی از این موضوع بهتر است مطلبهای آتی فرادرس در این مبحث را مطالعه کنید.
آزمون جذر
۱. کدام ویژگی اصلی عدد مربع کامل باعث میشود جذر آن یک عدد صحیح باشد؟
همواره کوچکتر از ده است.
عددهای فرد را شامل میشود.
فقط به عدد ۴ ختم میشود.
میتوان آن را به صورت ضرب عددی در خودش نوشت.
دلیل اینکه جذر یک عدد مربع کامل عدد صحیح است این است که میتوان آن عدد را به صورت ضرب یک عدد صحیح در خودش نوشت، مانند ۲۵=۵×۵.
۲. کدام مورد تعریف درست جذر (ریشه دوم) یک عدد مثبت و نماد ریاضی آن را بیان میکند؟
جذر عدد مثبت یعنی عددی که اگر با خودش جمع شود، همان عدد را میدهد و با نماد نمایش مییابد.
جذر عدد مثبت یعنی عددی که اگر تقسیم بر دو شود، همان عدد را میدهد و با نماد مشخص میشود.
جذر عدد مثبت یعنی عددی که اگر به توان دو برسد، همان عدد را میدهد و با نماد نوشته میشود.
جذر عدد مثبت یعنی عددی که اگر از آن کم کنیم، صفر میشود و با نماد نمایش داده میشود.
تعریف درست جذر (ریشه دوم) برای یک عدد مثبت این است که عددی باشد که اگر به توان دو برسد، همان عدد حاصل میشود و این عملیات با نماد ریاضی نمایش داده میشود.
۳. در فرایند یافتن جذر یک عدد مربع کامل و جذر یک عدد غیرمربع، چه تفاوت اصلی وجود دارد؟
برای اعداد مربع کامل جذر عددی صحیح است اما برای اعداد غیرمربع جذر معمولا عددی اعشاری بهدست میآید.
برای هر دو گروه فقط با تجزیه به عوامل اول میتوان جذر را بهدست آورد.
برای اعداد مربع کامل تنها جذر مثبت یافت میشود اما برای غیرمربعها جذر منفی هم وجود دارد.
برای اعداد غیرمربع فقط باید روش هندسی استفاده شود اما برای اعداد مربع کامل هر روشی مجاز است.
تفاوت اصلی این است که جذر اعداد مربع کامل مانند چهار یا بیستوپنج، همیشه یک عدد صحیح بهدست میدهد، اما جذر اعداد غیرمربع مانند پنج یا ده، معمولا عددی اعشاری (غیر دقیق و کسری) خواهد بود. عبارت «جذر عددی صحیح است» فقط درباره مربع کامل صادق است. جذر منفی برای هیچکدام تعریف نمیشود مگر در حوزه اعداد مختلط که اینجا بررسی نشده است. روش هندسی و تجزیه به عوامل اول، بهتنهایی برای یک گروه محدود نمیشوند و مؤلف پیشنهاد داده از چند روش مختلف برای آموزش و محاسبه استفاده شود.
۴. برای استفاده از قضیه فیثاغورس جهت نمایش هندسی و محاسبه جذر یک عدد مثبت، کدام اقدام مناسبتر است؟
تقسیم عدد مثبت به دو بخش مساوی و پیدا کردن میانگین آنها
استفاده از پرگار برای رسم نیمدایره به مرکز عدد مثبت
رسم یک مثلث قائمالزاویه با وتر برابر با جذر عدد مورد نظر روی محور اعداد
جمع دو خط روی محور اعداد به اندازه عدد مثبت و جذر آن
در این روش، با استفاده از قضیه فیثاغورس، ابتدا مثلث قائمالزاویهای رسم میشود که یکی از اضلاع آن عدد مثبت مورد نظر باشد. سپس با قرار دادن این ضلع بر روی محور اعداد، وتر این مثلث را محاسبه یا نمایش میدهیم که همان جذر عدد است. کاری مانند «جمع خطوط» یا «تقسیم عدد به بخشهای مساوی» با اصل محاسبه هندسی جذر ارتباطی ندارد و استفاده از پرگار بهتنهایی تنها هنگامی پاسخگو است که بخشی از رسم مثلث و نمایش وتر باشد، نه خود مرحله کلیدی. پاسخ درست، «رسم یک مثلث قائمالزاویه با وتر برابر با جذر عدد مورد نظر روی محور اعداد» است.
۵. برای محاسبه جذر عدد صحیح بزرگی مانند ۹۷۲ بدون ماشینحساب، کدام روش از نظر کارایی و استفاده عملی بهتر است؟
نوشتن جذر به صورت ضرب اعداد مربع کامل نزدیک
استفاده از روش هندسی با مثلث قائمالزاویه و کشیدن محور اعداد
استفاده از تجزیه به عوامل اول برای بیان جذر به شکل سادهتر
بکارگیری الگوریتم نیوتن-رافسون برای تخمین عددی جذر
در مورد محاسبه جذر عدد صحیح بزرگ بدون ماشینحساب، «بکارگیری الگوریتم نیوتن-رافسون برای تخمین عددی جذر» انتخاب مناسبتری است. روش تجزیه به عوامل اول تنها برای اعداد با تقسیمپذیری ساده عملی است و برای اعداد بزرگتر کارایی بالایی ندارد، زیرا تجزیه آنها وقتگیر است و همیشه به جواب دقیق عددی منجر نمیشود. الگوریتم عددی مانند نیوتن-رافسون امکان یافتن جذر با دقت دلخواه را فقط با چند گام ساده و فرمولاسیون تکراری فراهم میکند. استفاده از «نوشتن جذر به صورت ضرب اعداد مربع کامل نزدیک» یا روشهای هندسی برای اعداد خیلی بزرگ معمولا عملی نیستند و دقت کافی را هم ندارند.
۶. دقت و سرعت الگوریتم نیوتن-رافسون برای محاسبه جذر عدد مربع کامل مثل ۲۵ نسبت به عدد غیرمربع مثل ۱۰ چگونه مقایسه میشود؟
برای هر دو عدد، سرعت و دقت الگوریتم تقریبا یکسان است.
یافتن جذر عدد مربع کامل سریعتر و دقیقتر همگرا میشود.
الگوریتم برای عدد غیرمربع نسبت به عدد مربع کامل سریعتر به جواب میرسد.
محاسبه جذر عدد غیرمربع همواره نتیجه دقیقتری میدهد.
در روش عددی نیوتن-رافسون (Newton-Raphson)، برای عدد مربع کامل مثل «۲۵» الگوریتم خیلی سریعتر و با دقت بالا به مقدار دقیق جذر (که عدد صحیح است) همگرا میشود. در مقابل، برای اعداد غیرمربع مثل «۱۰»، الگوریتم باید گامهای بیشتری طی کند و به عدد تقریبی برسد، چون جذر عدد غیرمربع یک عدد اعشاری بیانتها است. بنابراین عملکرد این الگوریتم برای اعداد مربع کامل سریعتر و پاسخ نهایی دقیقتر خواهد بود، بهویژه با حدس اولیه مناسب. برای جذر اعداد غیرمربع، همواره به تقریب عددی نیاز است و هرگز مقدار دقیقی مانند عدد صحیح به دست نمیآید.













چرا باید داشته باشه؟
کشیدن خطی به طول یه عدد گنگ کاملا امکان پذیره.
چرا اینقدر شیوه فرمول نویسی تون عجیبه؟ نشانه های به کار رفته اصلا قابل دریافت توسط ذهن نیستند و فقط سردرگمی ایجاد می کنه! نمی دونم چرا از زبان استاندارد و جهانی ریاضی استفاده نکردید.
سلام بر شما دوست و همراه گرامی،
برای نوشتن فرمولهای ریاضی در محیط اینترنت و وب، باید از نرمافزارهای خاصی استفاده کرد که بتوانند الگو و نمادهای ریاضی را با قالب HTML سازگار سازند. بسیاری از مرورگرهای وب، مانند کروم یا موزیالا، این امکان را دارند که از ابزارهای هماهنگ سازی فرمول ها با محیط وب بهره ببرند. صفحات مجله فرادرس که دارای فرمول های ریاضی هستند به خوبی در مرورگرهای به روز و جدید اینترنت خوانده میشوند. بنابراین پیشنهاد می کنیم که مطالب علمی ریاضی مجله فرادرس را به کمک این گونه مرورگرها مطالعه کنید.
با سپاس فراوان
خیلی خوب بود اما میشه بگید مثلا رادیکال 25 به توان دو را به این صورت حل کرد
توان دو با رادیکال از بین بره و جواب آخر بدستبیاد که میشه 25
؟؟
به صورت کلی میشه گفت توان تقسیم بر فرجه میشه و عدد میاد بیرون.
ولی خب یه جاهایی نمیشه. مثلا رادیکال (-25) به توان دو میشه 25 و نه -25
واقعا عالی دست شما درد نکنه
خوب بود.ولی کاش تو ویدیو ها یکم واضح ترتوضیح میداد ن تیتروار بخونه وبره/:
ممنون از معلومات مفید تان
چرا وقتی با فیثاغورس میشه رادیکال ۲ رو بدست اوریم عدد ۲ جذر کامل نداره