سیمپلکس در اکسل – راهنمای کاربردی
در بحث «بهینهسازی» (Optimization) و «برنامهریزی خطی» (Linear Programming)، الگوریتمهای متنوعی به کار میرود. یکی از روشها برای حل چنین مسئلههایی، تکنیک یا «روش سیمپلکس» (Simplex Method) است. خوشبختانه اکسل ابزاری برای پیادهسازی یا اجرای الگوریتم سیمپلکس در اختیار کاربران قرار داده است. هر چند این ابزار در هنگام نصب اکسل قابل استفاده نیست، ولی میتوان از طریق نصب افزونههای استاندارد، تکنیکهای حل برنامهریزی خطی و غیرخطی را به آن اضافه کرد. در این نوشتار به ابزار Solver و نحوه حل مسائل برنامهریزی خطی (LP) با روش سیمپلکس در اکسل اشاره خواهیم داشت.


به منظور آشنایی بیشتر با روش سیمپلکس و محاسبات مربوط به آن، بهتر است نوشتارهای دیگری از مجله فرادرس با عنوانهای روش سیمپلکس (Simplex) | به زبان ساده و دستگاه معادلات خطی و حل آن — به زبان ساده را مطالعه کنید. همچنین برای آشنایی بیشتر با نحوه کار با اکسل نیز خواندن مطالب آموزش اکسل — به زبان ساده و فرمول نویسی در اکسل – آموزش مقدماتی توصیه میشود.
سیمپلکس در اکسل
برای یک مدیر مالی، آگاهی از ارتباط بین ساعات فعالیت نیروی کاری و هزینهها با سود و درآمدهای شرکت اهمیت زیادی دارد. او با توجه به بودجه تصویب شده، باید بتواند برنامهریزی هزینهها را به شکلی انجام دهد که در آخر هر ماه پاسخگوی هیئت مدیره بوده و سود مورد نظر برای سهامداران را محقق کند.
یک مدیر مالی معمولا بوسیله تابعی که براساس مقدار نفر/ساعت صرف شده روی یک پروژه، دستمزد، هزینه خرید ماشین آلات تشکیل میشود، سعی میکند مقدار کمینه را با تغییر دادن این متغیرها، بدست آورد. از طرفی او باید با توجه به میزان تولید، ساعات کاری و هزینههای جاری، کاری کند که فروش شرکت (سودآوری) نیز به حداکثر برسد. بنابراین ایجاد یک موازنه بین هزینهها و از طرفی تولید و فروش، لازم است که معمولا این موضوع منجر یه یک مسئله برنامهریزی خطی شده و باید آن را حل کرد.
ابتدا بعضی از اصطلاحات مربوط به مسائل بهینهسازی و برنامهریزی خطی را مورد بررسی قرار داده، سپس با مطرح کردن یک مسئله بهینهسازی، آن را در محیط اکسل پیاده سازی کرده و به کمک ابزار Solver و الگوریتم سیمپلکس، حل میکنیم.
اصطلاحات مربوط به برنامهریزی خطی و سیمپلکس
برنامهریزی خطی یکی از شاخههای ریاضیات و در گروه محاسبات «بهینهسازی» (Optimization) و «برنامهریزی ریاضی» (Mathematical Programming) قرار میگیرد. به کمک این تکنیک، با توجه به منابع محدود در دسترس، سعی میشود یک «تابع هدف» (Objective Function) به حداکثر مقدار یا کمترین مقدار خود برسد. حتی ممکن است هدف از حل مسئله بهینهسازی، تعیین مقادیر پارامترهای مدل با توجه به مقدار ثابتی برای تابع هدف باشد. این کار البته با توجه به محدودیتهایی که برای تابع هدف یا پارامترهای مدل معرفی میشود، صورت خواهد گرفت.
در ادامه با بعضی از کلیدواژههای برنامهریزی خطی آشنا خواهیم شد.
- متغیرهای تصمیم (Decision Variables): در اغلب موارد در برنامهریزی خطی، متغیرهای تصمیم، باید مشخص شوند. در هنگام تعریف مسئله این متغیرها شناسایی شده و ممکن است مقادیر آن توسط مدیریت قابل کنترل بوده یا محدودیتهای برای مقادیر آن وجود داشته باشد. از این متغیرها برای تعریف تابع هدف استفاده میشود.
- تابع هدف (Objective Function): این قسمت از مسئله برنامهریزی خطی، یک تابع ریاضیاتی است که با متغیر و پارامترهای مختلف ساخته و ایجاد میشود. هر یک از متغیرها، در حقیقت همان متغیرهای تصمیم بوده که با ترکیب آنها، نیازهای مدیریتی توسط رابطه ریاضی تبیین میشود. معمولا قرار است تابع هدف، کمینه (در مورد هزینهها) یا بیشینه (در مورد سود) شود. واضح است که با تغییر مقادیر متغیرهای تصمیم این کار صورت خواهد گرفت.
- قیود (Constrains): قیود یک مسئله برنامهریزی خطی، توابعی از متغیرهای تصمیم هستند که امکانات و منابع در اختیار را مشخص میکنند. این قیدها معمولا به شکل نامساوی یا نامعادلات ریاضی نوشته میشوند.
- کران متغیرها (Variable Bounds): متغیرهای تصمیم در مدل برنامهریزی خطی به همراه قیدهای گفته شده، نمیتوانند هر مقداری را اختیار کنند در نتیجه معمولا کرانهایی به صورت برای آنها در نظر میگیرند.
از آنجایی که در این قسمت در مورد برنامهریزی خطی صحبت میکنیم، واضح است که هم تابع هدف و هم قیود به صورت یک تابع خطی از متغیرها نوشته میشوند. در مدلهای غیرخطی ولی رابطه بین متغیرها ممکن است به صورت توان ۲ یا تابع هدف به جای وجود عملگر جمعی بین متغیرهای تصمیم، به شکل ضربی نوشته شده باشد.
در ادامه به بررسی شیوه حل یک مسئله برنامهریزی خطی میپردازیم که براساس فعالیت یک شرکت تولید ماشین لباسشویی ساخته شده است. هدف در این مسئله «حداکثرسازی» یا «بیشینهسازی» (Maximization) تابع سود (Profit) است.
طرح یک مسئله بهینهسازی و حل آن به روش سیمپلکس در اکسل
شرکت X یک تولید کننده لوازم خانگی است که به تازگی دو مدل از دستگاه به نامهای Arket و Kallex تولید کرده است که با امکانات و ویژگیها متفاوتی عرضه میشوند. با توجه به نیاز بازار و هزینههای تولید، شرکت میخواهد بفهمد که میزان تولید هر یک از این ماشینهای لباسشویی چقدر باشد تا به بیشترین سود برسد. لازم به ذکر است که منابع شرکت برای تولید آنها به صورت زیر است:
- ساعت کاری: ۳۱۳۲ نفر-ساعت
- متراژ شلنگ: 1440 متر
- تعداد دیگ: ۲۰۰ عدد
فروش هر یک از ماشینهای لباسشویی مدل Arkel سودی برابر با ۳۵۰ هزار تومان و فروش مدل Kallex نیز سود ۳۰۰ هزار تومانی خواهد داشت. در عین حال تولید هر دستگاه Arkel نیاز به ۱۸ نفر ساعت و ۸ متر شلنگ به همراه یک دیگ دارد. در عین حال Kallex فقط به ۱۲ نفر ساعت کار و ۸ متر شلنگ و یک دیگ احتیاج دارد. جدول زیر این مقادیر و سود هر یک از این دستگاهها را نشان داده است.
| Arkel | Kallex | کل منبع در اختیار | |
| زمان کاری | 18 نفر ساعت | ۱۲ نفر ساعت | ۳۱۳۲ نفر ساعت |
| شلنگ مصرفی | ۶ متر | ۸ متر | ۱۴۴۰ متر |
| دیگ | ۱ واحد | ۱ واحد | ۲۰۰ |
| سود (هزار تومان) | ۳۵۰ | ۳۰۰ |
پیادهسازی مسئله سیمپلکس در اکسل
در کاربرگ نمایش داده شده در تصویر ۱، یک جدول اطلاعاتی را متناسب با مسئله مورد نظر ایجاد کردهایم.
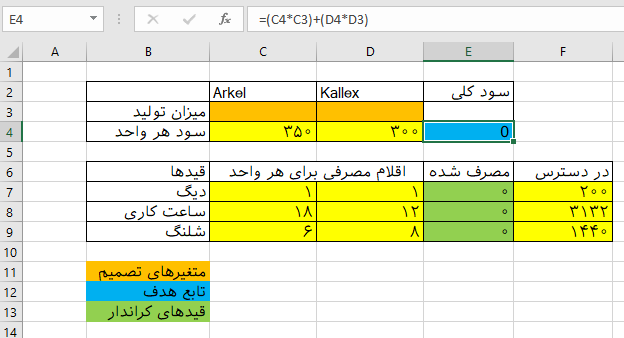
فرمولهایی که باید در این کاربرگ به کار رود نیز در ادامه مشخص شدهاند. همانطور که در تصویر ۱ نیز دیده میشود، سلولهای آبی و سبز رنگ، فرمولها را شامل میشوند.
سلولهای C7 تا C9، شامل تعداد قطعاتی است که برای تولید هر و احد از محصول Arkel مورد نیاز است. همچنین D7 تا D9 نیز ورودیهای مربوط به محصول Kallex را مشخص کرده. همچنین در سلولهای F7 تا F9 نیز میزان قطعات در دسترس برای هر یک از اقلام قید شده است. قیدها نیز در سلولهای E7 تا E9 نوشته شدهاند.
حل مسئله به روش سیمپلکس در اکسل به کمک Solver
به منظور راهاندازی Solver در اکسل، آن را از قسمت افزونهها Add-ins بارگذاری کنید. کافی است از فهرست File گزینه Options و قسمت Add-ins را انتخاب و از کادر سمت راست در قسمت Manage گزینه Excel Add-ins را انتخاب کرده و دکمه ...Go را کلیک کنید. سپس در پنجره Add-ins گزینه Solver را انتخاب و دکمه OK را بزنید.
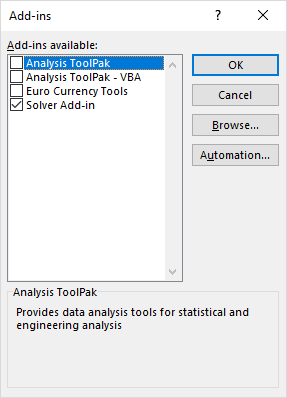
با طی کردن این مراحل، ابزار Solver در برگه Data در قسمت Analyze ظاهر میشود. با کلیک کردن روی آن به پنجره Solver دسترسی خواهید داشت. کافی است تنظیمات این پنجره را مطابق با فرمولهای گفته شده، مانند تصویر ۳، اجرا کنید.
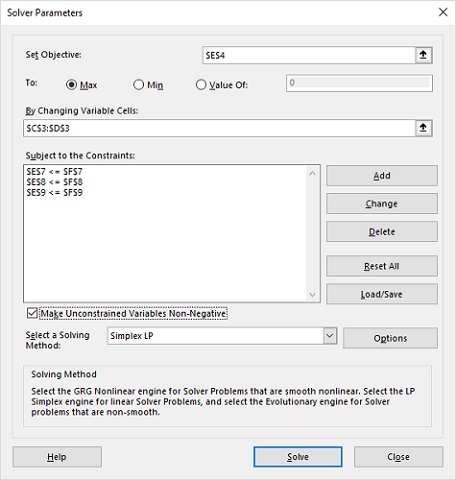
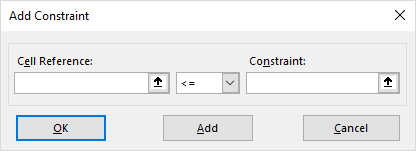
نکته: توجه داشته باشید که برای مشخص کردن قیدها در بخش Subject to the Constraints، از دکمه Add استفاده کنید. با تعیین سلول مربوط به قید در بخش Cell Reference و مقدار محدودیت مربوط به قید در Constraint، هر یک از قیود را ایجاد و دکمه Add را بزنید. بعد از اینکه آخرین قید را معرفی کردید، از دکمه OK استفاده کنید.
در انتها با انتخاب گزینه Simplex LP از بخش Select a Solving Method و فشردن دکمه Solve، اکسل مسئله برنامهریزی خطی را به روش سیمپلکس حل کرده و همگرایی و رسیدن به پاسخ مناسب را در یک پنجره مانند تصویر ۵، اعلام میکند.
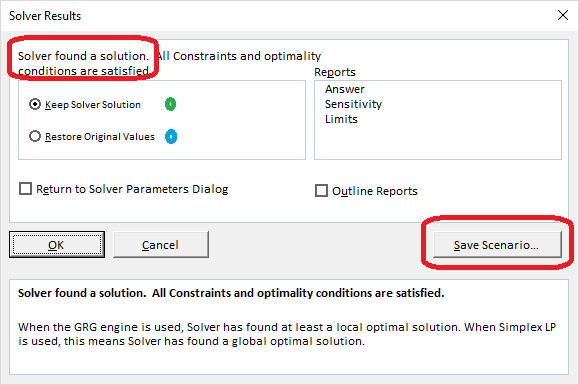
اگر در این پنجره گزینه Save Scenario را انتخاب نمایید، اکسل برای نمایش پاسخ (Answer) تحلیل حساسیت (Sensitivity) و همچنین مقادیر حدی (Limits) در کاربرگهای مجزا اقدام خواهد کرد، به شرطی که در قسمت Report آنها را انتخاب کرده باشید. همچنین با فعال کردن گزینه Keep Solver Solution، پاسخها در کاربرگ جاری جایگزین مقادیر قبلی شده و با فعال کردن Restore Original Values نیز مقادیر قبلی در سلولهای کاربرگ محاسباتی قرار میگیرند.
در تصویر زیر نتیجه و پاسخهای مربوط به حل این مسئله برنامهریزی خطی به روش سیمپلکس در اکسل دیده میشود.
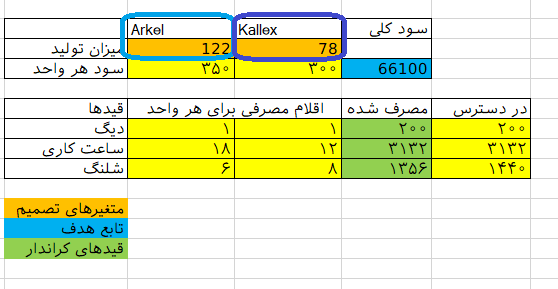
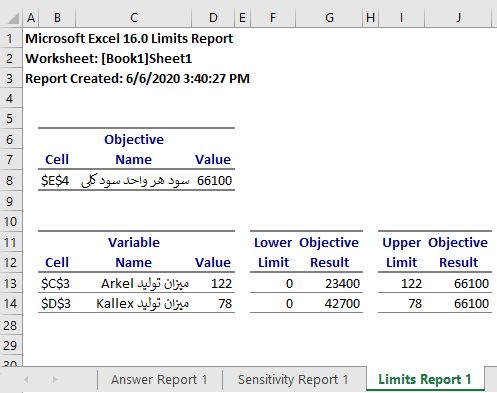
همانطور که در تصویر 6، مشاهده میکنید، تعداد ماشین لباسشویی Arkel برابر با 122 و ماشین لباسشویی Kallex نیز ۷۸ عدد در پاسخ ذکر شده است. با احتساب این مقادیر سود کلی برابر با ۶۶۱۰۰ هزار تومان خواهد بود. از طرفی دیده میشود که در قسمت کالاهای مصرف شده، همه اقلام به جز شلنگ به طور کامل به کار رفتهاند.
«گزارش پاسخ» (Answer Report)، «تحلیل حساسیت» (Sensitivity Report) و «گزارش کرانها و محدودیتها» (Limits Reports) نیز در ادامه قابل مشاهده هستند.
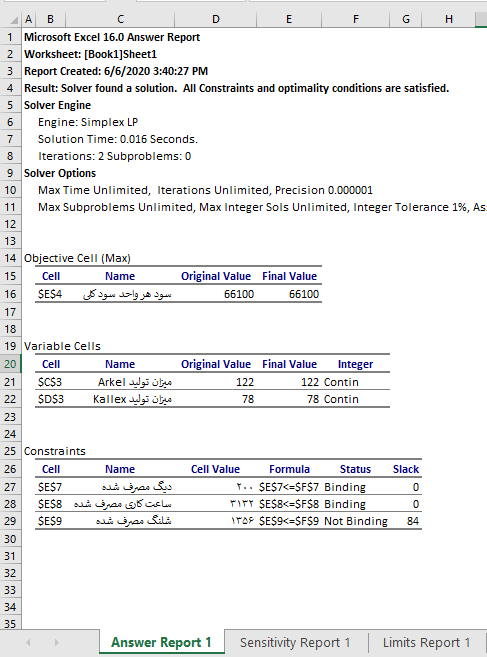
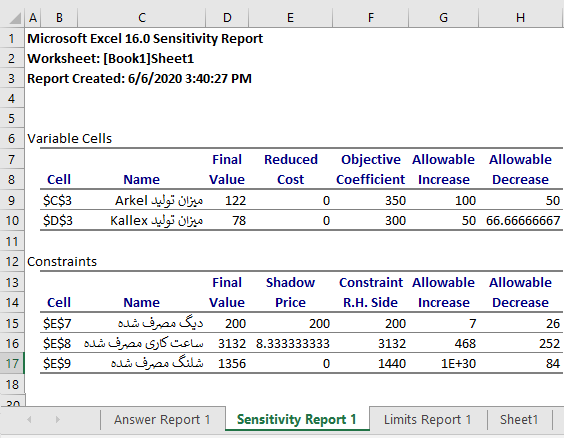
مطابق با تصویر ۷، در کاربرگ پاسخ (Answer Report)، مقادیر اولیه و همچنین پاسخها به همراه قیدهای مسئله ظاهر شدهاند. تحلیل حساسیت نیز در کاربرگ دیگری قرار میگیرد. به تصویر ۸ دقت کنید.
در انتها هم کاربرگ کرانها نیز محدودیتهای مربوط به قیدها به همراه مقدار تابع هدف، مطابق با تصویر ۹، ظاهر خواهد شد.
به منظور راحتی کاربران و خوانندگان این مطلب، کاربرگ مربوط به حل این مسئله را با قالب فشرده در اینجا قرار دادهام. با دریافت این فایل و خارج کردن آن از حالت فشرده، فایل simplex method in excel.xlsx را در اکسل باز کرده و میتوانید فرمولها و پنجره Solver را مشاهده کنید.
خلاصه و جمعبندی
در این نوشتار با دستگاه معادلات خطی و حل آنها، روشهای بهینهسازی و روش سیمپلکس آشنا شدید. به کمک مثالهایی که در محیط اکسل و ابزار Solver ارائه کردیم، چگونگی استفاده از روش سیمپلکس در اکسل را هم فرا گرفتیم. همانطور که مشاهده کردید، اکسل قادر است به سادگی مسائل بهینهسازی خطی را حل کرده و پاسخها را به صورت یک برگه به نام «سناریو» (Scenarios) ارائه نماید.












سلام
ممنون و سپاسگزارم از آموزش کاملتون.
لطفا بنده را راهنمایی بفرمایید که خروجی سلور بنده صرفا اعداد صحیح باشد بدون اعشار.
با تشکر.