خمش الاستوپلاستیک | با مثال های کاربردی

در مباحث «تحلیل تنش برشی در تیرهای بال پهن»، «تحلیل خمش در تیرهای نامتقارن» و «تعیین تنش برشی در تیرهای جدار نازک با مقطع باز» تیرهایی را مورد بررسی قرار دادیم که مواد سازنده آن‌ها از قانون هوک پیروی می‌کرد (مواد الاستیک خطی). در این مقاله به بررسی خمش در تیرهای الاستوپلاستیک خواهیم پرداخت. در انتها نیز چند مثال کاربردی را درباره خمش الاستوپلاستیک تشریح خواهیم کرد.

مقدمه

توزیع تنش در تیرهای الاستوپلاستیک، به صورت خطی نیست و با توجه به شکل منحنی تنش کرنش تغییر می‌کند. در مبحث «تحلیل الاستو پلاستیک در سازه های معین و نامعین استاتیکی»، مواد الاستوپلاستیک را مورد بررسی قرار دادیم. همان‌طور که در آن مبحث نیز اشاره شد، این مواد قبل از رسیدن به تنش تسلیم σ_Y، از قانون هوک پیروی می‌کنند. سپس تحت تنش ثابت به صورت پلاستیک تسلیم می‌شوند. با توجه به شکل زیر می‌توان مشاهده کرد که مواد الاستوپلاستیک دارای یک محدوده الاستیک خطی در میان نواحی پلاستیک کامل خود هستند. در این مقاله فرض می‌کنیم تنش تسلیم σ_Y و کرنش تسلیم ϵ_Y در هر دو حالت کشش و فشار برابر است.

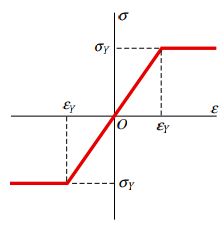
فولاد سازه‌ای را می‌توان به عنوان یکی از بهترین مثال‌های مواد الاستوپلاستیک در نظر گرفت؛ چراکه در نمودار تنش-کرنش این فولاد نقاط تسلیم به طور کامل مشخص هستند و کرنش‌های بزرگی در حین تسلیم رخ می‌دهند. نهایتاً، رفتار سخت شوندگی کرنش در این مواد شروع به می‌شود و دیگر فرض پلاستیسیته کامل برای آن‌ها معتبر نخواهد بود. سخت شوندگی کرنش امکان افزایش مقاومت را فراهم می‌کند. از این‌رو، فرض پلاستیک کامل بسیار خوش‌بینانه است.

گشتاور تسلیم

شکل زیر، یک تیر ساخته شده از مواد الاستوپلاستیک را نمایش می‌دهد که در معرض گشتاور خمشی M قرار گرفته است.

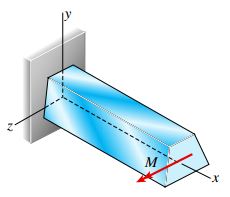
گشتاور M باعث ایجاد خمش در صفحه x-y می‌شود. در صورت کوچک بودن گشتاور خمشی، حداکثر تنش موجود در تیر از تنش تسلیم σ_Y کمتر و وضعیت آن مشابه یک تیر تحت خمش الاستیک با توزیع تنش یکنواخت (شکل زیر) خواهد بود.

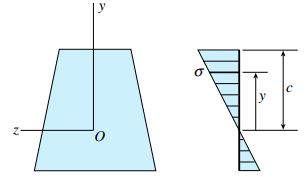
در این شرایط، محور خنثی از مرکز هندسی سطح مقطع عبور می‌کند و تنش‌های نرمال از طریق رابطه خمش (σ=M_y/I) محاسبه می‌شوند. به دلیل مثبت بودن گشتاور خمشی، تنش‌های بالای محور z فشاری و تنش‌های پایین این محور کششی هستند. حالت قبل تا زمانی باقی می‌ماند که تنش موجود در دورترین نقطه از محور خنثی (در فشار یا کشش) به تنش تسلیم σ_Y برسد (شکل زیر).

گشتاور خمشی در لحظه رسیدن به تنش تسلیم با عنوان «گشتاور تسلیم» (Yield Moment) شناخته شده و با M_Y نمایش داده می‌شود. مقدار این گشتاور از رابطه زیر به دست می‌آید:

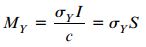
c: دورترین فاصله از محور خنثی؛ S: مدول مقطع مربوطه

گشتاور پلاستیک و محور خنثی

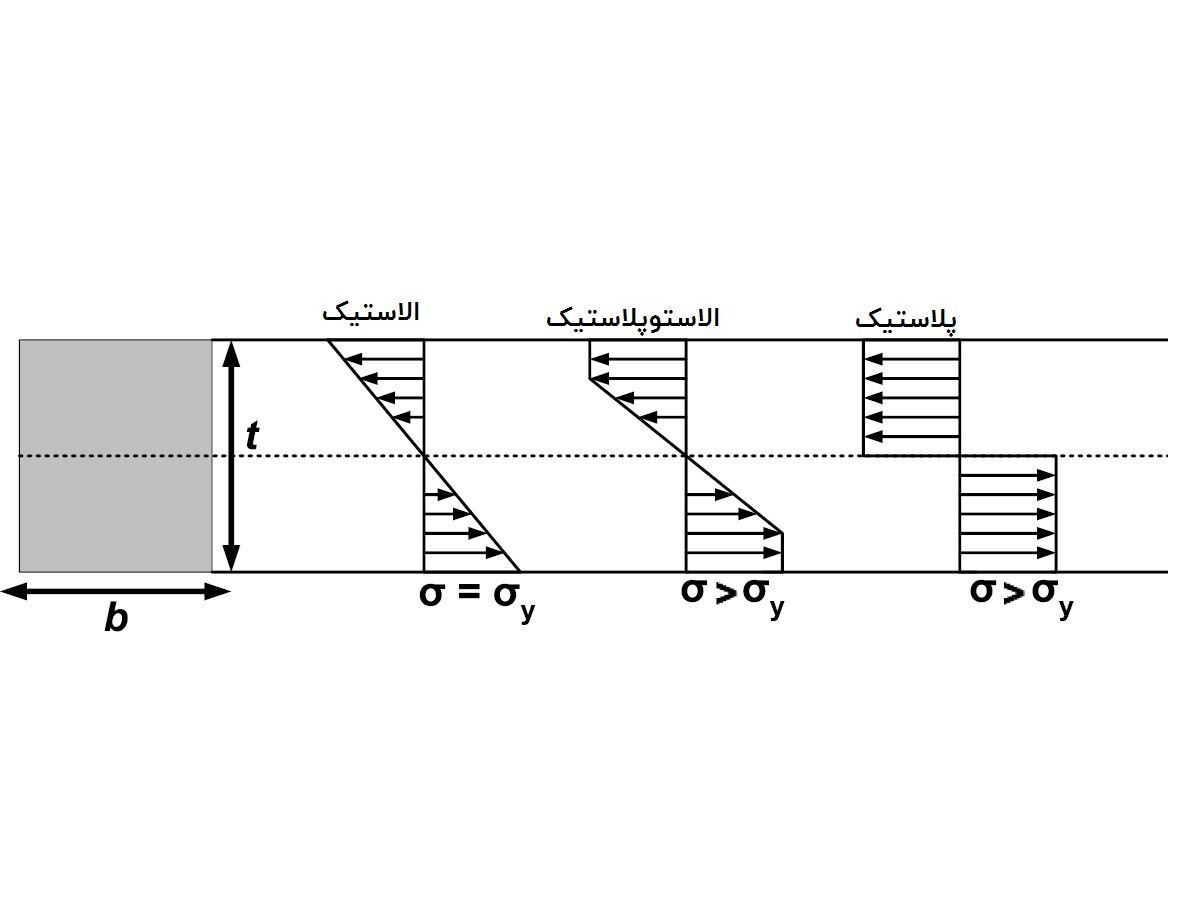
هنگامی که گشتاور خمشی از گشتاور تسلیم M_Y بیشتر می‌شود، کرنش درون تیر همچنان افزایش می‌یابد و مقدار حداکثری آن به کرنش تسلیم ε_Y می‌رسد. اگرچه به دلیل رخ دادن تسلیم پلاستیک کامل، مقدار تنش ماکسیمم ثابت و برابر σ_Y باقی می‌ماند (شکل زیر). توجه داشته باشید که در این حالت، نواحی خارجی تیر به صورت کاملاً پلاستیک و در مقابل هسته مرکزی آن (هسته الاستیک) به صورت الاستیک خطی باقی می‌ماند.

فیلم آموزش مقاومت مصالح – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

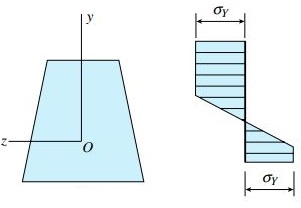
اگر محور تقارن سطح مقطع بر روی محور z منطبق نباشد، هنگام عبور گشتاور از نقطه تسلیم، محور خنثی از مرکز هندسی سطح مقطع دور می‌شود. جابجایی محور خنثی برای مقطع ذوزنقه‌ای بزرگ نبوده و به اندازه‌ای کوچک است که در شکل آن مشاهده نمی‌شود. در مقاطع دارای تقارن مضاعف، محور خنثی در هنگام عبور گشتاور از نقطه تسلیم نیز از مرکز هندسی سطح مقطع عبور می‌کند. با افزایش بیشتر گشتاور خمشی، ناحیه پلاستیک بزرگ‌تر و به محور خنثی نزدیک‌تر می‌شود. این تغییرات تا رسیدن به حالت نمایش داده شده در شکل زیر ادامه می‌یابند. در این مرحله، حداکثر کرنش موجود در تیر (در دورترین فاصله از محور خنثی) حدود 10 تا 15 برابر کرنش تسلیم ε_Y و هسته الاستیک تقریباً محو می‌شود.

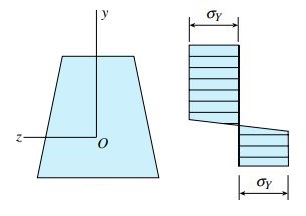
به این ترتیب، ظرفیت تیر برای مقاومت در برابر گشتاور به مقدار نهایی می‌رسد و وضعیت نهایی توزیع تنش (توزیع تنش ایده آل) به شکل دو مستطیل در می‌آید (شکل زیر). گشتاور خمشی متناظر با این توزیع تنش با عنوان «گشتاور پلاستیک» (Plastic Moment) شناخته شده و با علامت M_P نمایش داده می‌شود. این گشتاور بیانگر حداکثر گشتاوری است که یک تیر الاستوپلاستیک می‌تواند تحمل کند.

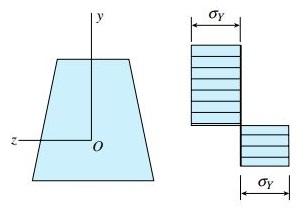
برای محاسبه گشتاور پلاستیک M_P، ابتدا باید مختصات محور خنثی سطح مقطع تیر را تحت شرایط کاملاً پلاستیک تعیین کرد. به این منظور، سطح مقطع نمایش داده شده در شکل زیر را با فرض انطباق محور خنثی بر روی محور z در نظر بگیرید.

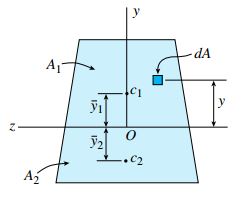
تمام نقاط موجود در بالای محور خنثی تحت تنش فشاری σ_Y و تمام نقاط زیر این محور تحت تنش کششی σ_Y قرار دارند (شکل زیر). برآیند نیروی فشاری C برابر با حاصل‌ضرب σ_Y در مساحت سطح مقطع A₁ (بالای محور خنثی) و برآیند نیروی کشش T برابر با حاصل‌ضرب σ_Y در مساحت سطح مقطع A₂ (پایین محور خنثی) است.

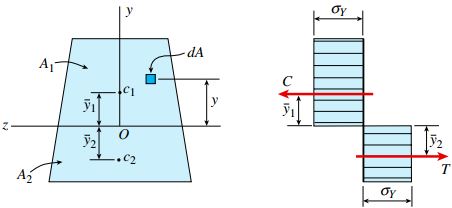
به دلیل صفر بودن نیروی برآیند اعمال شده بر روی سطح مقطع، خواهیم داشت:

مساحت کل سطح مقطع A از حاصل جمع A₁ و A₂ به دست می‌آید. بنابراین:

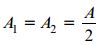
از این‌رو در شرایط کاملاً پلاستیک، محور خنثی سطح مقطع را به دو ناحیه برابر تقسیم می‌کند. به همین دلیل، امکان متفاوت بودن محل قرارگیری محور خنثی برای گشتاور پلاستیک M_P با خمش الاستیک خطی وجود دارد. به عنوان مثال، در مقاطع ذوزنقه‌ای که عرض سطح مقطع بخش بالایی کمتر از بخش پایینی است؛ محور خنثی در حالت خمش کاملاً پلاستیک کمی پایین‌تر از محور خنثی در حالت خمش الاستیک خطی خواهد بود.

به دلیل برابر بودن گشتاور پلاستیک M_P با برآیند گشتاور تنش‌های اعمال شده بر سطح مقطع، مقدار M_P از انتگرال بر روی سطح A تعیین می‌شود:

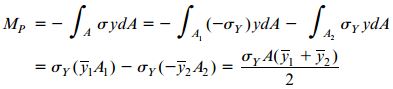
y: مختصات المان سطح dA (با فرض مثبت بودن جهت رو به بالا)؛ y^-₁ و y^-₂؛ فاصله محور خنثی تا مراکز هندسی سطوح A₁ و A₂ (نقاط c₁ و c₂)

روش ساده‌تر محاسبه گشتاور پلاستیک، استفاده از گشتاور نیروهای C و T حول محور خنثی است:

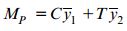
با جایگذاری روابط C و T داریم:

این رابطه همان رابطه حاصل از انتگرال‌گیری بر روی سطح A است. فرآیند اصلی محاسبه گشتاور پلاستیک شامل تقسیم سطح مقطع تیر به دو ناحیه مساوی، تعیین محل قرارگیری مرکز هندسی هر یک از نواحی و استفاده از رابطه بالا می‌شود.

ضریب شکل و مدول پلاستیک

رابطه به دست آمده برای گشتاور پلاستیک را می‌توان بر حسب رابطه گشتاور تسلیم نیز بازنویسی کرد:

که در آن:

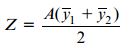
Z، مدول پلاستیک سطح مقطع است. از نظر هندسی، این مدول را می‌توان به عنوان گشتاور اول سطح بالای محور خنثی به علاوه گشتاور اول سطح زیر محور خنثی در نظر گرفت. نسبت گشتاور پلاستیک به گشتاور تسلیم فقط تابعی از شکل سطح مقطع بوده و با عنوان «ضریب شکل» (Shape Factor) شناخته می‌شود:

این ضریب، معیاری از مقاومت ذخیره شده در تیر بعد از شروع اولین تسلیم است. مقدار ضریب شکل برای مواردی که بخش زیادی از سطح مقطع در نزدیکی محور خنثی قرار داشته باشد (مانند تیری با سطح مقطع دایره‌ای توپر) دارای بیشترین مقدار و برای مواردی که بخش زیادی از سطح مقطع در فاصله دور از محور خنثی قرار داشته باشد (مانند تیری با سطح مقطع بال پهن) دارای کمترین مقدار است. نحوه تعیین مقادیر f برای سطح مقطع‌های مستطیلی، بال پهن و دایره‌ای در بخش‌های بعدی تشریح خواهد شد.

سطح مقطع تیر مستطیلی

شکل زیر، یک تیر با سطح مقطع مستطیلی را نمایش می‌دهد. جنس این تیر از مواد الاستوپلاستیک و مدول مقطع آن S=bh²/6 است.

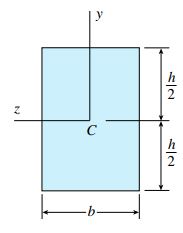
بنابراین، گشتاور تسلیم تیر بالا از رابطه زیر به دست می‌آید:

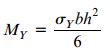
b: عرض سطح مقطع؛ h: ارتفاع سطح مقطع

به دلیل وجود تقارن مضاعف در سطح مقطع مستطیلی، محور خنثی آن در تمام محدوده‌های بارگذاری (الاستیک یا پلاستیک) از مرکز هندسی عبور می‌کند. از این‌رو، فاصله مراکز هندسی نواحی بالا و پایین تا محور خنثی برابرند با:

به این ترتیب، مدول پلاستیک برابر است با:

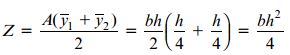
و برای گشتاور پلاستیک داریم:

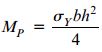
در نهایت، ضریب شکل مقطع مستطیلی از رابطه زیر به دست می‌آید:

یعنی گشتاور پلاستیک یک تیر مستطیلی 50 درصد بزرگ‌تر از گشتاور تسلیم است. اکنون تنش‌های موجود در یک تیر مستطیلی را برای حالتی در نظر بگیرید که گشتاور خمشی M بزرگ‌تر از گشتاور تسلیم بوده اما به گشتاور پلاستیک نرسیده باشد. در این شرایط، بخش‌های خارجی تیر تحت تنش تسلیم σ_Y و بخش‌های داخلی (هسته الاستیک) در معرض تنش با تغییرات خطی هستند (شکل زیر). نواحی پلاستیک کامل با رنگ خاکستری و فاصله محور خنثی تا لبه داخلی این نواحی با حرف e نمایش داده شده است.

تنش‌های اعمال شده بر سطح مقطع دارای نیروی برآیند T₁ ،C₂ ،C₁ و T₂ هستند. هر یک از نیروهای C₁ و T₁ در نواحی پلاستیک با حاصل‌ضرب تنش تسلیم در مساحت این نواحی برابری می‌کند:

نیروهای C₂ و T₂ در ناحیه هسته الاستیک نیز برابر با حاصل‌ضرب مساحت این ناحیه بر روی نمودار تنش در عرض b هستند:

به این ترتیب، برای گشتاور خمشی داریم:

توجه داشته باشید که اگر e=h/2 باشد، M=M_Y و در صورتی که e=0 باشد، M=3M_y/2 یا همان گشتاور پلاستیک M_P خواهد بود. در صورت مشخص بودن ابعاد هسته الاستیک می‌توان رابطه بالا را برای تعیین گشتاور خمشی به کار برد. با این وجود، معمولاً از گشتاور خمشی به منظور محاسبه اندازه هسته الاستیک استفاده می‌شود. بنابراین، اگر این رابطه را بر حسب گشتاور خمشی بازنویسی کنیم؛ خواهیم داشت:

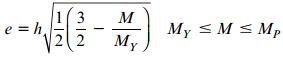
در اینجا نیز توجه داشته باشید که بر اساس شرایط مرزی اگر M=MY باشد، e=h/2 و در صورتی که M=MP=3M_Y/2 یا در حالت پلاستیک کامل باشد، e=0 خواهد بود.

سطح مقطع تیر بال پهن

شکل زیر، یک تیر بال پهن با تقارن مضاعف را نمایش می‌دهد. مدول پلاستیک Z این تیر از گشتاور اول سطح یکی از بال‌ها به علاوه گشتاور اول بخش بالایی جان و ضرب مقدار به دست آمده در 2 تعیین می‌شود.

فیلم آموزش مقاومت مصالح – ویژه رشته عمران در فرادرس

کلیک کنید

شکل ساده‌تر رابطه بالا را می‌توان به صورت بازنویسی کرد:

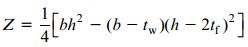
به این ترتیب، مدول پلاستیک از رابطه بالا و گشتاور پلاستیک با قرار دادن Z در رابطه M_P=σ_YZ به دست می‌آید. مقادیر Z برای انواع مختلف تیرهای بال پهن را می‌توان در منابع مختلف یافت. ضریب شکل f برای تیرهای بال پهن معمولاً از مقدار 1.1 تا 1.2 تغییر می‌کند. این مقدار به نسبت بین بخش‌های سطح مقطع تیر بستگی دارد. به منظور تحلیل تیرهای دارای اشکال دیگر نیز می‌توان از فرآیندی مشابه با فرآیند تشریح شده در این بخش استفاده کرد.

مثال‌های کاربردی خمش الاستوپلاستیک

به منظور آشنایی بیشتر و بهتر با روابط معرفی شده، در این بخش به تشریح دو مثال کاربردی خواهیم پرداخت.

مثال 1

شکل زیر، سطح مقطع یک تیر دایره‌ای به همراه قطر آن را نمایش می‌دهد. گشتاور تسلیم، مدول پلاستیک، گشتاور پلاستیک و ضریب شکل این تیر را محاسبه کنید.

برای شروع تحلیل در نظر داشته باشید که به دلیل وجود تقارن مضاعف در سطح مقطع دایره‌ای، محور خنثی در هر دو حالت الاستیک و الاستوپلاستیک از مرکز دایره عبور می‌کند. گشتاور تسلیم M_Y از رابطه خمش به دست می‌آید:

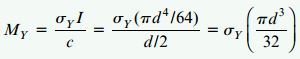
مدول پلاستیک از رابطه Z=A(y^-₁+y^-₂)/2 محاسبه می‌شود. در این رابطه، A مساحت دایره و y^-₁ و y^-₂ فاصله مراکز هندسی c₁ و c₂ (مرکز هندسی نیمه‌های بالایی و پایینی) تا مرکز دایره هستند.

برای محاسبه این پارامترها برای سطح مقطع دایره‌ای توپر از روابط زیر استفاده می‌کنیم:

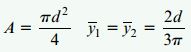
با جایگذاری روابط بالا در رابطه Z داریم:

به این ترتیب، گشتاور پلاستیک M_P برابر است با:

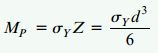
در نهایت، ضریب شکل نیز به صورت زیر تعیین می‌شود:

نتیجه بالا نشان می‌دهد که حداکثر گشتاور خمشی برای یک تیر دایره‌ای توپر از جنس مواد الاستوپلاستیک، حدود 70 درصد بزرگ‌تر از گشتاور خمشی آن در شروع فرآیند تسلیم است.

مثال 2

در شکل زیر، یک تیر مستطیلی توخالی با تقارن مضاعف از جنس مواد الاستوپلاستیک (σ_Y=33ksi) را نمایش می‌دهد که تحت گشتاور خمشی M قرار دارد. مقدار گشتاور خمشی به اندازه‌ای است که بال‌های تیر به نقطه تسلیم می‌رسد اما جان‌های آن در حالت الاستیک خطی باقی می‌ماند. اگر ابعاد سطح مقطع b=5in ،b₁=4 ،h=9 و h₁=7.5in باشد، مقدار گشتاور M را تعیین کنید.

سطح مقطع تیر مورد بررسی و توزیع تنش‌های نرمال اعمال شده بر روی آن در شکل زیر نشان داده شده است. با توجه به شکل می‌توان مشاهده کرد که مقدار تنش‌های موجود در جان‌های تیر با فاصله گرفتن از محور خنثی به صورت خطی افزایش می‌یابد. به علاوه، مقدار تنش‌های موجود در بال‌های تیر با تنش تسلیم σ_Y برابری می‌کند.

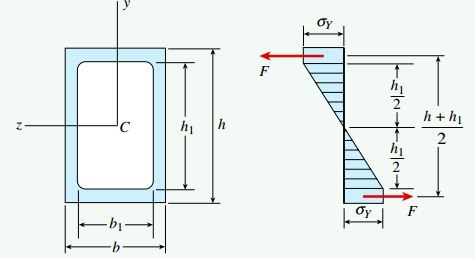
بنابراین، گشتاور خمشی M اعمال شده بر سطح مقطع دارای دو بخش خواهد بود:

• الف: گشتاور M₁ مربوط به هسته الاستیک
• ب: گشتاور M₂ حاصل از تنش‌های تسلیم σ_Y موجود در بال‌ها

گشتاور خمشی موجود در هسته با استفاده از رابطه خمش و مدول مقطع جان‌های تیر به دست می‌آید. به این ترتیب:

و

به منظور تعیین گشتاور موجود در بال‌های تیر باید در نظر داشته باشید که برآیند نیروی موجود در هر بال از حاصلظرب تنش تسلیم در مساحت بال به دست می‌آید:

اگر گشتاور خمشی مثبت باشد، نیروی موجود در بال بالایی به صورت فشاری و نیروی موجود در بال پایینی به صورت کششی خواهد بود. این دو نیرو باعث ایجاد گشتاور خمشی M₂ می‌شوند:

بنابراین، گشتاور کل اعمال شده بر سطح مقطع برابر است با:

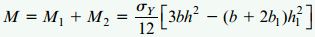
با جایگذاری مقادیر هر یک از پارامترها خواهیم داشت:

نکته: گشتاور تسلیم M_Y و گشتاور پلاستیک M_P دارای مقادیر زیر خواهند بود:

گشتاور خمشی M بین دو مقدار بالا قرار دارد.