تابع موج – به زبان ساده
پیشتر در مطلبی در وبلاگ فرادرس در مورد مکانیک کوانتومی صحبت کردیم. از این رو در این مطلب قصد داریم تا در مورد مفهومی از فیزیک کوانتومی تحت عنوان تابع موج صحبت کنیم. در حقیقت این تابع، اوپراتوری است که معادله شرودینگر بر مبنای آن نوشته میشود.


کوانتوم
مکانیک کوانتومی از نظر تاریخی به دو دوره مختلف اطلاق میشود. دوره اول مربوط به اندک زمانی پس از معرفی مفهوم دوگانگی موجی-ذرهای است. به طور دقیقتر میتوان گفت این دوره سالهای بین ۱۹۰۰ تا ۱۹۲۵ را شامل میشود. بخشهای اصلی دوره اول کوانتوم، مفهوم کوانتومی یا بستهای بودن انرژی و دوگانگی را مطرح میکند. در سال ۱۹۲۵، فیزیکدانی اتریشی به نام اروین شرودینگر، معادلهای ارائه داد که با استفاده از آن میشد حالت کوانتومی یک سیستم را تحلیل کرد.
ارائه معادله شرودینگر در حقیقت آغاز دوره دوم یا دوره مدرن مکانیک کوانتومی است. تابع موج را با نماد یا نمایش میدهند. این نماد با نام سای صدا زده میشود. توجه داشته باشید که نشانگر تابعی است که به طور همزمان وابسته به مکان و زمان و نشاندهنده تابع موجی است که تنها وابسته به مکان است.

اگر بخواهیم تعریفی دقیقتر را ارائه دهیم، میتوان گفت تابع موج نشاندهنده اوپراتوری است که در آن تمامی خواص کوانتومی یک ذره یا حتی در مواردی یک جسم نهفته است.
تابع موج
همانطور که در مطلب فوتون بیان شد، ذرات زیر اتمی خاصیتی موجی-ذرهای دارند. در حقیقت اگر انرژی یک ذره برابر با باشد، در این صورت میتوان فرکانس () برابر با مقدار زیر را به آن نسبت داده و آن را معادل با یک موج در نظر گرفت.
در رابطه فوق ، نشاندهنده عدد موج است. حال میخواهیم ذره را با استفاده از تابع موجی به صورت زیر تقریب بزنیم. شکل کلی تابع موجی همچون را به صورت زیر در نظر بگیرید.
به عبارت ریاضی ارائه شده در بالا که به یک ذره نسبت داده میشود، تابع موج میگویند. توجه داشته باشید که تابع موج را میتوان به صورت هریک از عبارتهای فوق نشان داد. به منظور درک بهتر تابع فوق باید ویژگیهای فیزیکی ذره را مورد بررسی قرار داد. برای نمونه با فرض اینکه فرکانس زاویهای و عدد موجِ یک ذره به ترتیب برابر با و باشند، در این صورت عددی تحت عنوان سرعت موج () را میتوان برابر با عبارت زیر تعریف کرد.
مقدار فوق در حقیقت بیان میکند اگر فرکانس و عدد موجِ یک موج معلوم باشد، در این صورت آن را میتوان معادل با ذرهای در نظر گرفت که سرعتش برابر با است. تابع موج بیانکننده احتمالی است که نشاندهنده حضور یک ذره در مکانی مشخص است. برای نمونه تابع موجی را به صورت زیر در نظر بگیرید.
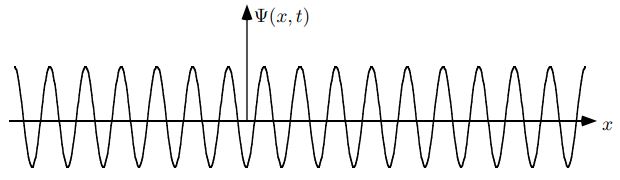
همانطور که مشاهده میکنید این تابع موج در تمامی نقاط به صورتی متقارن است. از این رو این تابع نمیتواند احتمالی خاص را در یک موقعیت خاص برای یک ذره تعیین کند.
بستههای موج
با توجه به آنچه که در بالا بیان شد، با استفاده از یک موج کاملا یکنواخت نمیتوان موقعیت یک ذره را در نقطهای خاص تعیین کرد. برای نمونه میتوان گفت یک جسم را میتوان با تابع موجی تقریب زد که تنها دارای یک قله تیز در یک نقطه است. برای نمونه در شکل زیر تابع موجی نشان داده شده که به خوبی مکان یک ذره یا جسم را نشان میدهد.
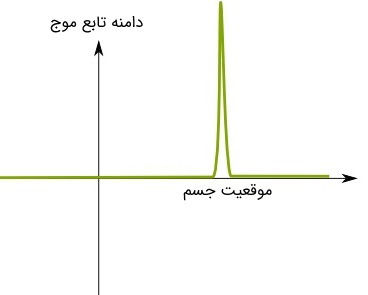
حال مسئله را به صورتی عکس در نظر بگیرید. فرض کنید که مکان دقیق یک جسم یا ذره معلوم بوده و میخواهیم برای آن تابع موجی تعیین کنیم که موقعیت آن را نشان دهد. همانگونه در بالا نیز بیان شد، این تابع باید تنها دارای یک قله باشد. از این رو این سوال مطرح میشود که چگونه میتوان با استفاده از توابعی دورهای (پریودیک) تکقلهای را همچون شکل فوق ایجاد کرد؟
برای پاسخ به سوال فوق فرض کنید دو موج با فرکانسهای نزدیک به هم را با هم جمع میکنیم. در این صورت موجی بدست میآید که قلههای آن تقویت شده و درههای آن نیز عمیقتر میشود.
حال فرض کنید بینهایت موج با اعداد موجِ با هم جمع شوند. مقادیر اعداد موج در بازه زیر قرار میگیرند.
توجه داشته باشید که نشاندهنده مقدار میانگین عدد موج است. بنابراین تابع موج به صورت زیر در نظر گرفته شده است.
مقدار نیز تابعی از است که مقدار ماکزیمم آن در رخ میدهد. با محاسبه حدِ جمعِ فوق و انتگرالگیری از آن، تابع موج برابر با انتگرال زیر بدست میآید.
در این صورت شکل موج به نحوی در خواهد آمد که در مرکز، دامنه ماکزیمم شده و هرچه از آن فاصله میگیریم، دامنه به صفر میل میکند. در شکل زیر نمودار دامنه تابع موج بر حسب و همچنین نمودار بر حسب موقعیتِ نشان داده شده است. به موجی به شکل زیر بسته موج گفته میشود.
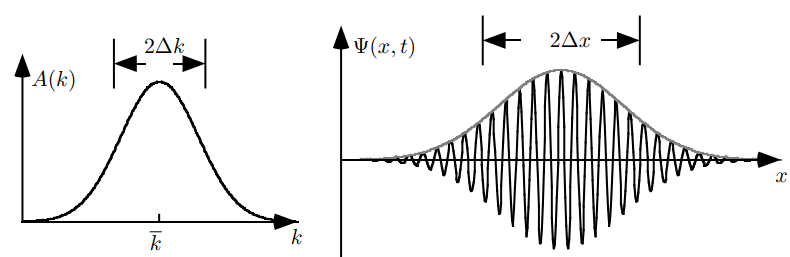
جالب است بدانید که تصویر سمت راست را میتوان به عنوان یک الکترون در نظر گرفت که خود آن نیز دارای سرعتی مشخص است. بسته فوق با جمع امواجی با عدد موج میانگینِ بوجود آمده است. از این رو میتوان این بسته را به ذرهای با تکانه نسبت داد. با این فرض سرعت موج نیز برابر با است. برای اثبات تکانه بدست آمده در بالا، باید توجه داشت که عدد موج به صورت پیوسته در نظر گرفته شده است. از این رو سرعت بسته را میتوان برابر با مشتق زیر در نظر گرفت.
سرعت فوق نشاندهنده سرعت بخشی از بسته است که در آن تمامی موجهای جمع زده شده همفاز هستند. همانطور که رابطه فوق نیز نشان میدهد برای بدست آوردن سرعت بسته باید رابطه بین و را بدست آورد. بدین منظور از مفهوم انرژی جنبشی به صورت زیر استفاده میکنیم. رابطهای تحت عنوان رابطه پاشش که نشاندهنده انرژی کل موج است به شکل زیر بیان میشود:
با قرار دادن رابطه فوق در رابطه دیبروی داریم (توجه داشته باشید که به جای انرژی نیز از رابطه پلانک استفاده شده):
از رابطه فوق میتوان عبارت زیر را نتیجه گرفت:
در نتیجه سرعت بسته برابر میشود با:
در ادامه مثالی ارائه شده که به منظور درک بهتر پیشنهاد میشود آن را مطالعه فرمایید.
مثال
تابع موج مربوط به یک الکترون آزاد را مطابق با رابطه زیر در نظر بگیرید.
با توجه به تابع فوق، مقدار طول موج دیبروی، مومنتوم، انرژی جنبشی و سرعت الکترون را در حالتی بیابید که عدد موج برابر با باشد.
روابط را بار دیگر با هم مرور میکنیم.
با توجه به ، مقادیر و برابرند با:
همچنین برای الکترونی با جرمِ ، مقادیر انرژی جنبشی و سرعت نیز برابر میشوند با:
در صورتی که مطلب فوق برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:













پس رابطه ی
Ψ(x,t)=A cos(Κχ-ωt)
احتمال حضور ذره ای در یک نقطه ی خاص فضا-زمان رو نشون میده؛درسته؟!
درواقع این تابع موج است حاصل ضرب تابع موج در مزدوج مختلط آن که میشود همان تابع موج به توان دو چگالی احتمال را نشان میدهد و اگر از این عبارت انتگرال بگیریم بعد به احتمال میرسیم
با سلام
یه سوالی داشتم
با توجه به اینکه الکترون میتواند در اوربیتال حرکت کند ولی احتمال حضور الکترون در گره اوربیتال(مثلاp) صفر است،چگونه این انتقال الکترون صورت میگیرد؟
الکترون خاصیت ذره ای_موجی دارد و زمانی که ما تابع موج را رسم میکنم حالت موجی الکترون است درواقع
درواقع مثلا اوربیتال p که بصورت دمبلی شکل در نظر گرفته میشود و یک گره دارد، براساس تابع موج و انرژی رسم شده نه براساس حرکت الکترون
درواقع در این حالت که در گره مقدار تابع موج صفر است، ما باید الکترون رو به حالت موجی در نظر بگیریم نه ذره
سلام و روز شما به خیر؛
انتقال الکترون در مکان صورت میگیرد (یعنی مختصات فضایی متفاوت) نه اوربیتالهای مورد بحث شما در یک جسم.
از اینکه با مجله فرادرس همراه هستید خرسندیم.
چون برای من نقاط مبهمی در متن وجود دارد بتدریج سؤالاتی را مطرح می کنم:
1. منظور از ” اوپراتور ” چیست؟
2. منظور از خواص کوانتومی ذره و جسم چیست؟
سلام.
۱. اپراتور یا عملگر در فیزیک کوانتوم به مشخصهای در یک سیستم نسبت داده میشود که قابل مشاهده است. برای مثال در مکانیک کلاسیک تکانه و مکان یک جسم به عنوان اپراتور یا عملگر شناخته میشوند.
۲. در مکانیک کوانتومی، یک ذره آزاد یا یک جسم با بردار موج تعریف میشود. ویژگیهای ذرهای یک جسم با اندازهگیری مکان و سرعت جسم در مکانیک کلاسیک مشخص میشود. ویژگیهای موجی جسم در مکانیک کوانتومی با اندازهگیری ویژگیهایی مانند تداخل موج تعریف میشوند. در حقیقت، منظور از خواص کوانتومی یک جسم که از تعداد زیادی ذره تشکیل شده، شناخت ویژگیهای موجی آن است. در مکانیک کلاسیک، شناخت ویژگیهای ذره شامل مکان، سرعت و … خواهد بود. در مکانیک کوانتومی نیز برای شناخت ذره باید ویژگیهای موجی ذره را بررسی کرد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
لطفا برای این جور مباحث فیلم هم قرار بدین خواهش میکنم