الگوریتم کروسکال چیست؟ – توضیح کراسکال به زبان ساده با مثال و کد
الگوریتم کروسکال یکی از الگوریتم های حریصانه در نظریه گرافها و ریاضیات گسسته است که برای پیدا کردن مقدار کمینه درخت پوشا از گراف داده شده همبند، وزندار و بدون جهت استفاده میشود. درخت پوشا زیرگرافی از گراف G(V,E) است. درخت پوشا تمام رئوس گراف داده شده را پوشش میدهد با این شرط که مجموع وزن یالهای درخت در کمترین حالت ممکن باشد. در موردی که گراف داده شده همبند نباشد با بهکار بردن الگوریتم کروسکال میتوان MST هر جزء همبند را پیدا کرد. میزان پیچیدگی زمانی الگوریتم کروسکال برابر با O(E∗log(E)) و پیچیدگی فضایی این الگوریتم O(E) است.
- یاد میگیرید چگونه مسائل واقعی را به گراف مدل کنید.
- میآموزید الگوریتم کروسکال را به صورت گامبهگام اجرا کنید.
- با استفاده از ساختار داده Disjoint-Set جلوگیری از حلقه را یاد خواهید گرفت.
- یاد میگیرید الگوریتم کروسکال را به زبانهای برنامهنویسی مختلف پیادهسازی کنید.
- خواهید آموخت پیچیدگی زمان و فضای الگوریتم کروسکال را تحلیل کنید.
- با کاربردهای عملی Minimum Spanning Tree و کروسکال در شبکهسازی آشنا میشوید.


در این مطلب از مجله فرادرس درباره الگوریتم کروسکال بحث کردهایم. اینکه این الگوریتم چیست، چطور کار میکند و چگونه میتوان این الگوریتم را پیادهسازی کرد. برای هر کدام مثالهای تصویری یا کدنویسی شده آوردهایم و در نهایت بعضی از مهمترین کاربردهای الگوریتم کروسکال را به صورت مختصر و شفاف توضیح دادهایم.
الگوریتم کروسکال چیست؟
فرض کنید در منطقه شهرستانی چند روستا وجود دارند. به عنوان شهردار کل منطقه، تصمیم به بازدید از تمام روستاها گرفتهایم. اما برای این کار زمان خیلی کمی در اختیار داریم. بنابراین میخواهیم همه روستاها را طوری بازدید کنیم که مسیر طی شده کمترین زمان ممکن شود.
در صورت تلاش برای فرمولنویسی مسئله مطرح شده بالا در مبحث نظریه گرافها فرمول مورد نظر را باید با توجه به موارد زیر پیادهسازی کنیم.
- در نظر گرفتن روستاها به عنوان رئوس گراف
- جادههای بین روستاها به عنوان یالهای گراف
- و مسافت هر جاده به عنوان وزن یال مربوطه
در چنین مواردی الگوریتم کروسکال به کمک حل مسئله میآید. بهطور کل الگوریتم کروسکال برای پیدا کردن « مقدار کمینه درخت پوشا» (Minimum Spanning Tree | MST) در گرافهای همبند وزندار غیر جهتدار بهکار میرود. قبل از بحث درباره جزئیات بیشتر الگوریتم کروسکال باید اول معنی مقدار کمینه درخت پوشا را در گراف درک کنیم.
برای مثال تصویر داده شده در پایین، گراف G را با شش راس و نُه یال نشان میدهد.
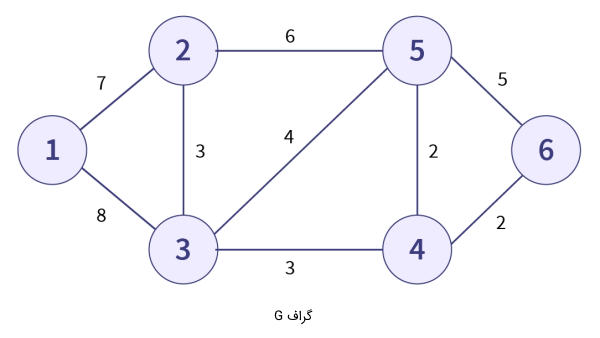
این گراف میتواند چندین درخت پوشا داشته باشد. بعضی از این درختها در تصاویر زیر همراه با هزینه مربوط به هر کدام نمایش داده شدهاند.

اما از آنجا که حداقل یک درخت پوشا با اندازه مجموع وزنهای کمتر وجود دارد، هیچ کدام از این درختهای پوشا درخت پوشای کمینه نیستند. درخت پوشای کمینه یا MST گراف بالا در تصویر زیر نمایش داده شده است.
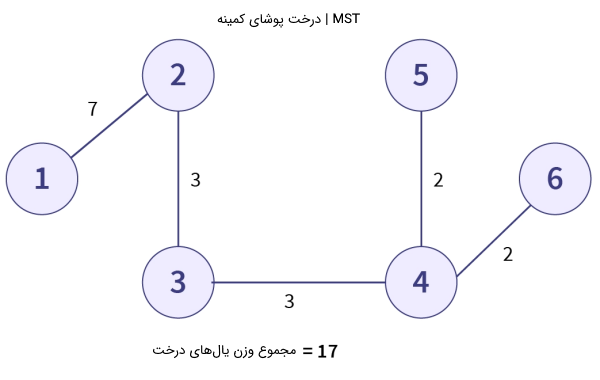
وزن MST گراف داده شده برابر با ۱۷ است. به این معنا که نمیتوانیم هیچ درخت پوشایی بر روی گراف G با وزن کمتر از ۱۷ پیدا کنیم.
روش های تسلط بر طراحی الگوریتم با فرادرس
الگوریتم کروسکال یکی از الگوریتمهایی است که برای حل مسائل مربوط به گرافها طراحی شده است. دنیای کامپیوتر پر است از این الگوریتمها و میتوان گفت حرفهایترین برنامهنویسان کسانی هستند که توانایی طراحی الگوریتمها را دارند. طراحی الگوریتم یکی از رشتههای تخصصی علوم کامپیوتر است. روشهای مختلفی برای آموزش طراحی الگوریتم وجود دارد، یکی از روشهای خوب استفاده از کلاسها و دورههای آموزشی است. باید توجه کنیم که فیلمهای آموزشی نسبت به کلاسها از مزیتهای بیشتری برخوردار هستند. فرادرس نیز به عنوان یکی از بزرگترین تولید کنندگان محتوا آموزشی فارسی، فیلمهای بسیار خوبی در زمینه طراحی الگوریتم ارائه داده است.
در ادامه، چند مورد از مزیتهای فیلمهای آموزشی را نسبت به کلاسهای حضوری فهرست کردهایم.
- مشکل اول این است که موسسات خیلی کمی برای آموزش طراحی الگوریتم وجود دارند.
- در صورت پیدا کردن چنین موسسهای هزینه مالی زیادتری نسبت به فیلمهای آموزشی باید متقبل شد.
- چنین کلاسهایی دارای زمانبندی مشخصی هستند که معمولا دانشجو مجبور به تنظیم زمان خود با موسسه است زیرا زمان کلاس با دانشجو تنظیم نمیشود.
- کیفیت آموزشی این کلاسها را بهجز از طریق کسب تجربه نمیتوان سنجید.
به این منظور و برای راهنمایی شما همراهان عزیز، فرادرس فیلمهای آموزشی زیادی را بهصورت اختصاصی در این باره تولید و منتشر کرده است که در ادامه چند مورد از آنها را معرفی کردهایم.
- فیلم آموزش طراحی الگوریتم فرادرس
- فیلم آموزش طراحی الگوریتم همراه با حل مثال های عملی فرادرس
- فیلم آموزش حل روابط بازگشتی در سایت فرادرس
- فیلم آموزش مروری بر پیچیدگی محاسبات در وب سایت فرادرس
پیاده سازی الگوریتم کروسکال
ایده اصلی الگوریتم کروسکال برای پیداکردن درخت پوشای کمینه یا MST گراف G با V راس و E یال در دو نکته کلی خلاصه شده که در ادامه فهرست کردهایم.
- باید همه یالها را به ترتیب صعودی مطابق بر وزنشان منظم بچینیم.
- سپس اولین دسته یالها به اندازه V−1 را انتخاب میکنیم، با این شرط که حلقهای توسط یالهای انتخاب شده تشکیل نشود.
برای یادگیری روش تقسیم و حل در طراحی الگوریتم میتوانید از فیلم آموزش روش تقسیم و حل همراه با مرور و تست کنکور کارشناسی ارشد در فرادرس که در ادامه به صورت لینک آمده استفاده کنید.
باید به این نکته توجه کرد که برای هر گراف با V راس، برای تشکیل MST فقط به V-1 یال نیاز داریم. زیرا برای اتصال همه راسها به هم V-1 یال کافی است.

در بخشهای بعد با مطالعه بیشتر الگوریتم و دیدن مثالها روش کار دقیق الگوریتم کروسکال را درک خواهیم کرد.
مراحل فرایند اجرای الگوریتم
برای هر گراف G=(V,E) پیدا کردن MST با استفاده از الگوریتم کروسکال شامل مراحل زیر میشود.
- همه یالهای گراف را بر اساس وزنشان به صورت صعودی مرتب میکنیم.
- یال با کمترین وزن را پیدا میکنیم. اگر اضافه کردن این یال به درخت پوشای جواب باعث ایجاد حلقه شود، این یال را از داخل جوابها حذف میکنیم. در غیر این صورت، یال پیدا شده را به جواب اضافه میکنیم.
- قدم بالایی را تا زمان رسیدن به تعداد V−1 یال ادامه میدهیم.
مثالی از الگوریتم کروسکال
در این سوال فرضی میخواهیم MST گراف را پیدا کنیم. شکل نمایش داده شده در تصویر زیر مر بوط به گراف پایه، همبند، وزندار و غیرجهتداری است که از ۶ راس و ۹ یال تشکیل شده.
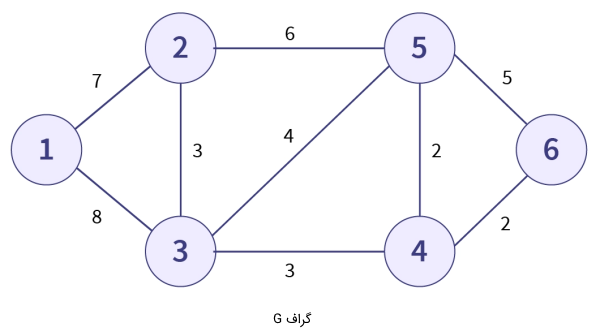
اکنون مطابق الگوریتم توصیف شده در بالا، برای پیدا کردن درخت پوشای کمینه این گراف باید مراحل زیر را طی کنیم.
- همه یالها را بر طبق وزنهای مربوط به هر کدام با نظم صعودی در جدولی به صورت مرتب قرار میدهیم.
- سپس اولین یال از دسته یالها به اندازه V−1=5 را انتخاب میکنیم. دستههای انتخاب شده نباید شامل شکل حلقه شوند.
- مرحله اول: مرتب کردن یالها با نظم صعودی. در جدول زیر میتوانیم فهرست یالها را بعد از مرتب کردن مشاهده کنیم.
| وزن | V | U | شماره یال |
| 2 | 5 | 4 | 1 |
| 2 | 6 | 4 | 2 |
| 3 | 4 | 3 | 3 |
| 3 | 3 | 2 | 4 |
| 4 | 5 | 3 | 5 |
| 5 | 6 | 5 | 6 |
| 6 | 5 | 2 | 7 |
| 7 | 2 | 1 | 8 |
| 8 | 3 | 1 | 9 |
- مرحله دوم: ۵ یال را از محل شروع جدول انتخاب میکنیم. البته به شرطی که این یالها با هم حلقه تشکیل ندهند.
- یال 4⟺5 را بررسی میکنیم. این اولین یال است. از آنجا که یال تنها نمیتواند حلقهای تشکیل دهد پس این یال را به گراف جواب اضافه میکنیم.
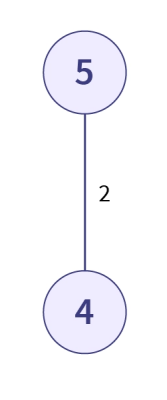
-
- سپس یالهای 3
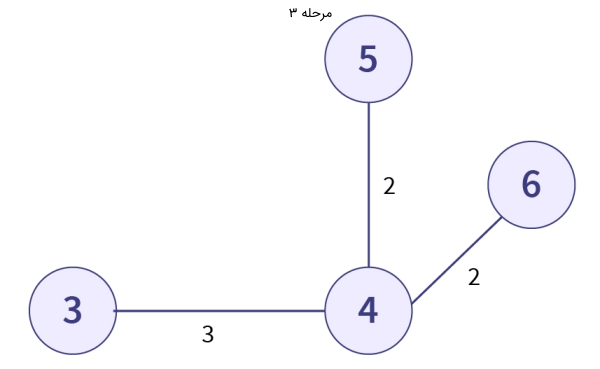
-
- این بار یال 2⟺3 را بررسی میکنیم. این بار هم

-
- این بار نوبت به بررسی یال 3

-
- این دفعه یال 5⟺6 را بررسی میکنیم. اضافه کردن این یال هم به جواب باعث ایجاد حلقه در گراف جواب میشود. بنابراین این یال را نیز به گراف جواب اضافه نمیکنیم.

-
- الان نوبت بررسی یال 2⟺5 است. اضافه کردن این یال نیز به گراف جواب باعث تشکیل حلقه 2→3→4→5→2 میشود. بنابراین این یال را نیز به گراف جواب اضافه نمیکنیم.

-
- در نهایت هم یال 1⟺2 را بررسی میکنیم. از آنجا که اضافه کردن این یال به گراف جواب باعث تشکیل حلقه نمیشود، بنابراین این یال را هم به جواب اضافه میکنیم. با اضافه کردن این یال، در کل ۵ یال را به گراف جواب اضافه کردهایم. در نتیجه الان گراف جواب بدست آمده مطابق با درخت پوشای کمینه این گراف است.
گراف MST بعد از اضافه کردن هر ۵ یال پیدا شده به شکل زیر میشود.
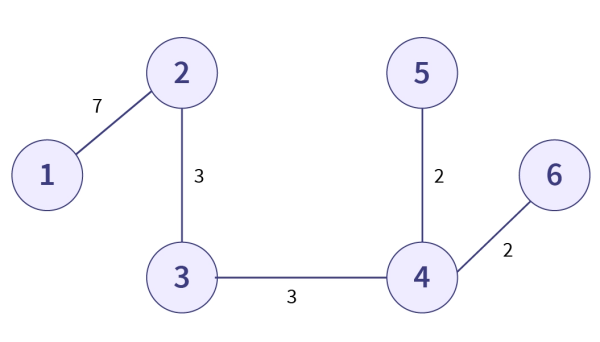
در نهایت وزن MST را نیز میتوان به سادگی با فرمول 7+3+3+2+2=17 بدست آورد.
مثال های کدنویسی شده الگوریتم کروسکال
در این بخش میخواهیم الگوریتم کروسال را با کمک کدنویسی پیادهسازی کنیم. برای انجام اینکار بهترین روش در ابتدا پیادهسازی «شبه کد» (Pseudocode) این الگوریتم است.
توجه کنید که در زبان های برنامه نویسی مختلف سینتکسها و ابزار متفاوتی برای کدنویسی موجود است، اما شبهکد، سینتکس جامع و خوانایی دارد. بنابراین همیشه بهتر است که در ابتدا شبهکد را پیادهسازی و درک کنیم و سپس از روی آن به پیادهسازی الگوریتمهای خود بپردازیم.
کد نمایش داده شده بالا پیادهسازی شبهکد الگوریتم کروسکال است. از روی شبهکد بالا میتوان این الگوریتم را به زبانهای مختلف پیادهسازی کرد.
مثال های کد نویسی شده با زبان های برنامه نویسی
برای بررسی موثرتر این مطلب که آیا شامل شدن یالی به جواب، باعث تشکیل حلقه میشود یا نه، از مفهومی به نام «مجموعههای مجزا» (Disjoint-Sets) استفاده خواهیم کرد. برای کدنویسی باید مطابق شبهکد و الگوریتم توصیف شده در بالا به پیش برویم. در وهله اول فهرست مرتبی از یالها را به صورت صعودی ایجاد میکنیم. سپس V−1 یال را به جواب اضافه میکنیم. البته توجه داریم که این یالها نباید در کنار یکدیگر حلقه تشکیل بدهند. قبل از اینکه یالی را به MST اضافه کنیم، از تابع find از DSU را برای بررسی تعلق یا عدم تعلق گرههای هر دو سر یال به مجموعه یکسان استفاده میکنیم.

اگر راسهای دوسر یال به مجموعه یکسانی تعلق نداشتند، آن وقت آن یال را به MST اضافه میکنیم. زیرا اضافه کردن این یال به گراف جواب MST باعث ایجاد حلقه نمیشود. اکنون از تابع «اتحاد» (Union) DSU برای ادغام دو مجموعه مجزا استفاده خواهیم کرد. در ادامه قبل از پرداختن به کدنویسی این الگوریتم، طرح اولیه آن را مشاهده میکنیم.
متغیرها
- V: متغیری سراسری که تعداد رأسهای گراف را نمایش میدهد.
- E: متغیر سراسری دیگری که تعداد یالهای درون گراف را محاسبه کرده و نشان میدهد.
- یالها: لیستی از یالها که بر اساس وزنشان به صورت صعودی مرتب شده است و در الگوریتم کروسکال استفاده میشود.
روش
- MST_Kruskal: تابعی که مسئول پیدا کردن MST در گراف داده شده است. این تابع طبق مطالب مطرح شده درباره الگوریتم در شبهکد بالا پیادهسازی شده است.
در صورتی که به پیادهسازی الگوریتمها به زبان برنامهنویسی و مبحث گرافها علاقهمند هستید، پیشنهاد میکنیم مطلب برنامه تشخیص وجود دور در گراف جهت دار همراه با راهنمای کاربردی را از مجله فرادرس مطالعه کنید. در این برنامه برای تشخیص وجود دور در گراف، الگوریتم طراحی شدهای را معرفی کردهایم. سپس این الگوریتم را به سه زبان برنامه نویسی پایتون، جاوا و ++C کدنویسی کردیم.
پیاده سازی الگوریتم کروسکال با زبان های C و ++C
در این بخش، برنامه کدنویسی شدهای با زبانهای C و ++C از روی طرح اولیه و الگوریتم کروسکال توصیف شده در بالا را مشاهده میکنید.
پیاده سازی الگوریتم کروسکال با زبان Java
در این بخش، برنامه کدنویسی شدهای به زبان جاوا، از روی طرح اولیه و الگوریتم کروسکال توصیف شده در مطلب را مشاهده میکنید.
تجزیه و تحلیل پیچیدگی زمانی و فضایی الگوریتم کروسکال
در این قسمت از مطلب، پیچیدگیهای این الگوریتم را به صورت کلی فرمول نویسی کردهایم. «پیچیدگی زمانی» (Time Complexity) الگوریتم کروسکال را میتوان با نکات زیر توصیف کرد.
- هزینه زمانی مرتب کردن E عدد یال برابر با O(E∗log(E)) است.
- برای هر یال، از الگوریتم Union-Find استفاده میکنیم که هزینه زمانی معادل O(E∗α(V)) بر عهده سیستم گذاشته میشود.
- در مقادیر عملی V، مقدار است. از آنجا که O(𝛼(𝑉)) عبارت O(E∗α(V)) را میتوان به صورت O(E) نیز نوشت.
بنابراین کل پیچیدگی زمانی این الگوریتم برابر با ≃
پیچیدگی فضایی این الگوریتم هم به این صورت است که چون از لیست یا برداری برای ذخیره E تعداد یال گراف داده شده استفاده میکنیم. پیچیدگی فضایی برابر با O(E) است.
فیلم های کمک درسی در رابطه با طراحی الگوریتم
طراحی الگوریتم یکی از دروس اصلی رشتههای مربوط به علوم کامپیوتر در دانشگاهها است. این قسمت از مطلب بهطور خاص مناسب دانشجویانی ارائه شده که نه تنها میخواهند بدانند که طراحی الگوریتم چیست بلکه باید برای آزمونهای دانشگاهی و کنکور ارشد نیز آماده شوند. وبسایت آموزشی فرادرس فیلمهای بسیار خوبی درباره الگوریتم با استفاده از اساتید حرفهای و تجزیه و تحلیل سوالات کنکور سالهای متمادی تهیه کرده است.
در این بخش چند مورد از این فیلمهای آموزشی را معرفی میکنیم. این فیلمها هم برای دانشجویان و برنامهنویسان و هم برای سایر افرادی که میخواهند با مبحث طراحی الگوریتم تا حد بسیار خوبی آشنا شوند مفید است.
- فیلم آموزشی طراحی الگوریتم همراه با مرور و تست کنکور ارشد فرادرس
- فیلم آموزش پیشرفته ساختمان داده به همراه حل سوالات کنکور ارشد و دکتری فرادرس
- فیلم آموزش روش تقسیم و حل در طراحی الگوریتم همراه با مرور و تست کنکور کارشناسی ارشد فرادرس
- فیلم آموزش رابطه های بازگشتی در طراحی الگوریتم و ساختمان گسسته بههمراه مرور و تست کنکور ارشد فرادرس
کاربردهای الگوریتم کروسکال
MST-هایی که توسط الگوریتم کروسکال پیدا میشوند کاربردهای فهرست شده در پایین را دارند.
- در طراحی شبکه، پیدا کردن MST حداقل مقدار سیم مورد نیاز را برای اتصال همه گرهها یا سرورهای شبکه، مشخص میکند.
- با استفاده از MST می توان مسئله فروشنده دورهگرد را نیز با تخمین بسیار خوبی حل کرد. این مسئله کارایی و عملکرد بسیار خوب مقدار کمینه درخت پوشا را برای حل چالشهای بهینهسازی پیچیده نشان میدهد.

- MST برای پیکربندی پروتکلهای Ethernet Bridging نیز استفاده میشود. استفاده از این درختهای پوشا از تشکیل حلقه در شبکهها جلوگیری میکند.
- تمام سایر مسائل گراف دیگری که در آنها باید تمام راسها را با حداقل هزینه بازدید کنیم نیز با استفاده از MST قابل حل است.
جمع بندی
در این مطلب از مجله فرادرس معنی عبارت درخت پوشا در گرافها همراه با درخت پوشای کمینه را با کمک مثالهای مختلف فهمیدیم. متوجه شدیم که الگوریتم کروسکال، از نوع الگوریتمهای حریصانه برای پیدا کردن درخت کمینه پوشا است. این الگوریتم بر روی هر گراف وزندار و غیرجهتدار همبندی کار میکند. همچنین آموختیم که چگونه MST گراف را با استفاده از الگوریتم کروسکال پیدا کنیم. در نهایت، پیچیدگیهای زمانی و فضای این الگوریتم را بررسی کردیم و با چند مورد از کاربردهای مهم این الگوریتم آشنا شدیم.
الگوریتم کروسکال یکی از مفاهیم مهم در نظریه گرافها و ریاضیات گسسته است که همینطور که دیدیم، میتواند بسیار از مسائل مربوط به شبکه را حل کند. شناخت و پیادهسازی و کارکردن با این الگوریتم تاثیر بسیاری در مهارت کدنویسی و حل مسئله برنامهنویسان دارد.