اصل برنولی چیست؟ — کاربردها + مثال

در بازی گلف به هنگام پرتاب توپ متوجه خواهید شد که توپ از مسیر سهمی‌شکل خود منحرف می‌شود. سوالی که مطرح می‌شود آن است که چرا توپ از مسیر اصلی خود منحرف می‌شود. با فرا گرفتن اصل برنولی می‌توان به این پرسش پاسخ داد. این اصل یکی از ساده‌ترین و در عین حال‌ مهم‌ترین اصل‌ها در علم فیزیک و مهندسی است. با کمک این اصل می‌توانیم جریان شاره‌ها را به خوبی درک کنیم و رابطه بین فشار، سرعت و ارتفاع شاره در حال حرکت را به دست آوریم. در این مطلب به زبان ساده اصل برنولی و کاربردهای آن را در زندگی روزمره فرا می‌گیریم.

اصل برنولی چیست ؟

اصل برنولی یا اثر برنولی یکی از مهم‌ترین نتیجه‌ها در مطالعه دینامیک شاره‌ها است. در این اصل، به رابطه بین سرعت حرکت شاره با فشار آن پرداخته می‌شود. در نگاه اول ممکن است اصل برنولی اهمیت چندانی نداشته باشد ولی به کمک آن می‌توانیم دلیل بسیاری از پدیده‌ها را توضیح دهیم. دینامیک شاره‌ها، مطالعه شاره در حال حرکت است. بنابراین، اصل برنولی و معادلات حاکم بر آن به تناوب در این زمینه مورد استفاده قرار خواهند گرفت.

اثر برنولی توسط فیزیکدان و ریاضی‌دان سوییسی به نام «دنیل برنولی» (Daniel Bernouli) توسعه داده شد. این اصل با استفاده از پایستگی انرژی، رابطه بین فشارِ شاره را با سرعت و ارتفاع آن بیان می‌کند. در واقع، بر طبق این اصل اگر سرعت شاره‌ای افزایش یابد، آن‌گاه فشار شاره یا انرژی پتانسیل آن کاهش می‌یابند.

با کمک اصل برنولی می‌توان دلیل حرکت شاره‌ها را بیان کرد. شاره به دلیل اختلاف ارتفاع (تغییر انرژی پتانسیل) یا اختلاف فشار در قسمت‌های مختلف سیستم حرکت می‌کند. در نتیجه، شاره‌ها از ناحیه‌ای با انرژی و فشار بیشتر به ناحیه‌ای با فشار کمتر حرکت می‌کنند.

نکته: بر طبق این اصل، شاره‌ای که سریع‌تر حرکت می‌کند فشار کمتری خواهد داشت.

بیان اصل برنولی

بیان ساده اصل برنولی به صورت زیر خواهد بود:

شاره در حال حرکت با سرعت بیشتر، فشار کمتری نسبت به شاره در حال حرکت با سرعت کمتر دارد.

بنابراین در لوله آب افقی با قطر متغیر، ناحیه‌ای که در آن آب با سرعت بیشتری حرکت می‌کند دارای فشار کمتری خواهد بود. از آنجایی که این دیدگاه وجود دارد که در سرعت‌های بالا فشار نیز بالا خواهد بود، بنابراین بیان اصل برنولی برای افرادِ بسیاری قابل درک نیست. در ادامه نشان خواهیم داد این دیدگاه راه دیگری برای بیان این موضوع است: جریان آب هنگامی سرعت می‌گیرد که فشار بیشتری در پشت آن قرار داشته باشد. 

قبل از توضیح بیشتر در مورد این اصل، این سوال مطرح می‌شود که چرا جریان شاره در لوله افقی در نظر گرفته شد. به دلیل نادیده گرفتن تغییراتِ نیروی گرانشی، لوله به صورت افقی در نظر گرفته می‌شود. در صورت جریان شاره در لوله عمودی، تغییرات نیروی گرانشی نیز باید در نظر گرفته شود.

نرخ جریان حجمی و معادله پیوستگی

قبل از اثبات معادله برنولی، در ادامه کمی در مورد معادله پیوستگی و مفهوم آن صحبت خواهیم کرد.

مطابق تصویر نشان داده شده در ادامه مطلب، لوله ای را با سطح مقطع متغیر در نظر بگیرید. محل ورودی شاره به لوله دارای سطح مقطع $$A_i$$ و محل خروج شاره از لوله دارای سطح مقطع $$A_o$$ است. همچنین فرض کنید شاره با سرعت $$v_i$$ به لوله وارد می‌شود.

سوالی که مطرح می‌شود آن است که پس از گذشت زمان T چه حجمی از شاره در لوله جابجا خواهد شد. با توجه به معادله‌های حرکت نیوتن داریم:

$$d= vt$$

در نتیجه پس از گذشت زمان ‌‌T، شاره به اندازه $$d= v_i T$$ داخل لوله جابجا می‌شود (حجم سبز).

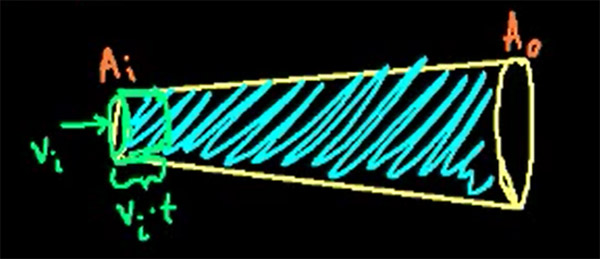
حجم استوانه سبز به صورت زیر به دست خواهد آمد:

$$V_i = A_i v_iT$$

از آنجایی که فرض می‌کنیم شاره داخل لوله، تراکم‌ناپذیر است در نتیجه حجم شاره ورودی به لوله با حجم خروجی از لوله برابر خواهد بود.

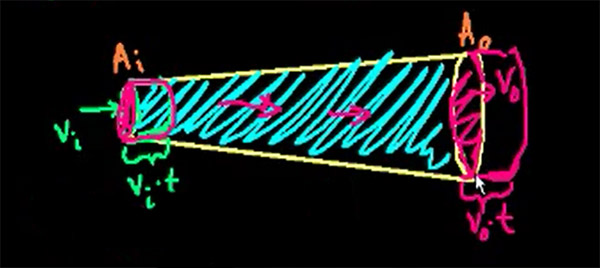
حجمی از شاره که از لوله خارج می‌شود به صورت زیر به دست می‌آید:

$$V_o = A_o v_oT$$

حجم شاره ورودی برابر با حجم شاره خروجی است:

$$V_i = V_o \\ A_i v_iT = A_o v_oT \ \Rightarrow A_iv_i = A_ov_o$$

به رابطه به دست آمده در بالا، معادله پیوستگی گفته می شود.

اکنون کمیت جدیدی به نام «شار» (Flux) را تعریف می‌کنیم:

شار: مقدار حجمی از شاره که در مدت زمان t از سطح مشخصی عبور می‌کند. 

$$Flux = \frac{V}{t}$$

مثال معادله پیوستگی

در ادامه برای درک بهتر معادله پیوستگی، مثالی را در این زمینه حل می‌کنیم.

پرسش:

آشپزی به منظور کسب اطمینان از داشتن شیر نارگیل برای پخت کیک، لوله‌ای استوانه‌ای را از انبار به آشپزخانه نصب کرد. سر لوله با شعاع 4 سانتی‌متر در انبار قرار دارد و شیر نارگیل با سرعت 0/25 متر بر ثانیه وارد آن می‌شود. اگر شیر نارگیل با سرعت 1 متر بر ثانیه از انتهای لوله (انتهای لوله در آشپزخانه قرار دارد) خارج شود، شعاع انتهای لوله را به دست آورید.

پاسخ:

معادله پیوستگی به صورت زیر نوشته می‌شود:

$$A_1v_1 = A_2v_2$$

از آنجایی که سطح مقطع استوانه به صورت $$\pi r^2$$ محاسبه می‌شود، بنابراین با قرار دادن آن در رابطه بالا داریم:

$$\pi (r_1^2)v_1 = \pi (r_2^2)v_2$$

با حذف $$\pi$$ از دو طرف رابطه بالا داریم:

$$(r_1)v_1 = (r_2^2)v_2 \\ \\ (r_2^2) = (r_1^2) \frac{v_1}{v_2} \\ r_2 = (r_1^2) \ \sqrt{\frac{v_1}{v_2}}$$

با قرار دادن داده‌های پرسش در رابطه بالا خواهیم داشت:

$$r_2 = (4\ cm) \ \sqrt{\frac{0.25 \ \frac{m}{s}}{1.0 \ \frac{m}{s}}} \Rightarrow \ r_2 = 2 \ cm$$

مقدمه‌ای بر معادله برنولی

شاره‌های تراکم‌ناپذیر به هنگام رسیدن به بخش باریک‌تر، به منظور حفظ نرخ حجم عبوریِ، سریع‌تر حرکت خواهند کرد. به این دلیل، آبی که در شلنگ جریان دارد به هنگام عبور از نازل باریک متصل به سر شلنگ با سرعت بیشتری حرکت می‌کند. با افزایش سرعت جریان آب، انرژی جنبشی نیز افزایش خواهد یافت. در اینجا این سوال مطرح می‌شود که منشا افزایش انرژی جنبشی از کجاست، لوله یا نازل؟

با انجام کار بر روی جسم می‌توان به آن انرژی جنبشی داد. این جمله به زبان ریاضی به صورت زیر نوشته می‌شود.

$$W_{external}=\triangle K = \frac{1}{2}mv_f^2\ - \ \frac{1}{2}mv_i^2$$

بنابراین هنگامی که سرعت بخشی از شاره افزایش می‌یابد، عامل خارجی باید بر روی آن کار انجام دهد. با چه نیرویی بر روی شاره کار انجام می‌شود؟ در سیستم‌های واقعی، نیروهای اتلافی زیادی قادر به انجام کار منفی هستند، اما به منظور ساده کردن سیستم‌های واقعی، مقدار این نیروهای اتلافی را بسیار کوچک در نظر می‌گیریم. در این صورت، شاره به آرامی و پیوسته به صورت لایه‌های موازی بدون عبور از مسیرهای مختلف در جریان خواهد بود. ولی سوالی که مطرح می‌شود آن است که این ساده‌سازی سیستم‌های واقعی تا چه اندازه به واقعیت نزدیک است؟

در نظر گرفتن شاره‌ای با جریان آرام، بدون آشوب و بدون اتلاف انرژی، فرضیه‌ای است که در مقایسه با سیستم‌های واقعی بسیار متفاوت خواهد بود. «هوراسی لمب» (Horace Lamb) در سال 1895 مقاله‌ای در مورد پیچیدگی دینامیک شاره‌ها در مقایسه با دیگر مباحث فیزیکی منتشر کرد.

در توضیحات بالا اشاره کردیم که هیچ اتلاف انرژی به دلیل نیروهای اتلافی نخواهیم داشت. در نتیجه، نیروهای غیراتلافی بر روی شاره مورد نظر کار انجام می‌دهند و موجب افزایش سرعت آن می‌شوند. در واقع، اگر ناحیه‌ کوچکی از شاره را در نظر بگیریم، فشار ناشی از شاره اطراف بر این ناحیه نیرو وارد می‌کند.

تصویر زیر جریان آب را در لوله‌ مشخصی نشان می‌دهد. هنگامی که حجم معینی از آب به قسمت کوچک‌تر لوله وارد می‌شود، سرعت جریان آب افزایش خواهد یافت. با در نظر گرفتن جهت مثبت به سمت راست، به حجم مورد نظر که وارد ناحیه کوچک‌تر شده است دو نیرو وارد می‌شود.

1. نیروی ناشی از فشار $$P_1$$ در سمت چپ حجم مورد نظر که بر روی این ناحیه کار مثبت انجام می‌دهد.
2. نیروی ناشی از فشار $$P_2$$ در سمت راست حجم مورد نظر که بر روی این ناحیه کار منفی انجام می‌دهد.

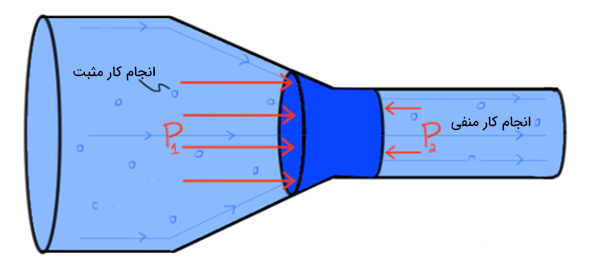
به دلیل معادله پیوستگی، جریان آب با سرعت بیشتری حرکت می‌کند و در نتیجه کار انجام شده بر روی آن مثبت خواهد بود. از این‌ رو کار انجام شده از طرف نیروی ناشی از فشار $$P_1$$ در سمت چپ باید بیشتر از کار منفی انجام شده از طرف نیروی ناشی از فشار $$P_2$$ در سمت راست باشد. این بدان معنا است که فشار در ناحیه با قطر بزرگ‌تر ($$P_1$$) بیشتر از فشار در ناحیه با قطر کوچک‌تر ($$P_2$$) است.

نکته: به رابطه معکوس بین فشار و سرعت در یک نقطه‌ مشخص در شاره، اصل برنولی گفته می‌شود.

بر طبق اصل برنولی، شاره به هنگام عبور از ناحیه‌ای با فشار بیشتر به ناحیه‌ای با فشار کمتر شتاب خواهد گرفت.

به جمله زیر دقت کنید:

ناحیه‌‌ای که در آن شاره با سرعت حرکت می‌کند، فشار کمتری خواهد داشت.

مفهوم جمله بالا کمی عجیب به نظر می‌رسد. هنگامی که در رودخانه‌ای با جریان آب سریع شنا کنید، نیروی زیادی از سمت جریان آب بر شما وارد خواهد شد. ولی باید به این نکته توجه کنیم که ما در اینجا در مورد دو فشار متفاوت صحبت می‌کنیم. فشاری که در اصل برنولی به آن اشاره می‌شود فشار داخلی شاره است که به دلیل جریان شاره در تمامی جهت‌ها وارد می‌شود. این فشار با فشار وارد شده از سمت شاره بر ما تفاوت دارد.

معادله برنولی چیست ؟

معادله برنولی حالت کلی‌تر و صورت ریاضی اصل برنولی است که در آن تغییرات انرژی پتانسیل گرانشی نیز در نظر گرفته شده است. معادله برنولی را در بخش‌های بعد به دست خواهیم آورد. در این قسمت مفهوم این معادله بررسی خواهد شد.
معادله برنولی فشار، سرعت و ارتفاع دو نقطه‌ از شاره‌ای با جریان یکنواخت و با چگالی $$\rho$$ را به یکدیگر مربوط می‌کند. معادله برنولی به طور معمول به صورت زیر نوشته می‌شود.

$$P_1+\frac{1}{2}\rho v_1^2+\rho g h_1=P_2+\frac{1}{2}\rho v_2^2+\rho g h_2$$

در رابطه بالا $$P_1,h_1,v_1$$ نشان‌دهنده سرعت، ارتفاع و فشار در نقطه ۱ و $$P_2,h_2,v_2$$ بیان‌گر سرعت، ارتفاع و فشار در نقطه ۲ خواهند بود (تصویر نشان داده شده در ادامه). ذکر این نکته مهم است که معادله برنولی برای هر دو نقطه‌ای در شاره صادق خواهد بود.

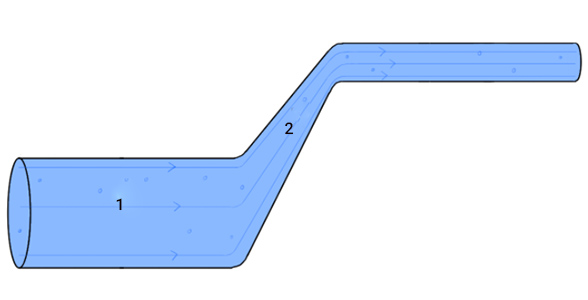
سوالی که مطرح می‌شود آن است که به هنگام استفاده از معادله برنولی، نقاط مورد نظر را چگونه انتخاب می‌کنیم. انتخاب نقاط به طور معمول به صورت زیر خواهد بود:

• یکی از نقاط را ناحیه‌ای در نظر بگیرید که یکی از مجهول‌های مساله در آنجا قرار گرفته است.
• نقطه دوم در ناحیهای انتخاب می‌شود که اطلاعات مساله در آنجا قرار دارد. این نقطه می‌تواند سطحی از شاره باشد که با هوا در تماس است (در این نقطه فشار جو مشخص خواهد بود).

برای اندازه‌گیری ارتفاع h، سطحی را به عنوان سطح مرجع انتخاب می‌کنیم و هر ارتفاعی نسبت به این سطح اندازه‌گیری می‌شود. به طور معمول، از بین دو نقطه ۱ و ۲، ارتفاع نقطه‌ای که کمتر است، صفر در نظر گرفته می‌شود. در این صورت، ارتفاع نقطه دوم نسبت به نقطه پایین‌تر سنجیده خواهد شد.

عبارت‌های $$\frac{1}{2}\rho v^2$$ و $$\rho g h$$ در معادله برنولی شبیه انرژی جنبشی ($$\frac{1}{2} m v^2$$) و انرژی پتانسیل ($$m g h$$) هستند. تنها تفاوت در آن است که چگالی جانشین جرم شده است. در نتیجه، معادله برنولی با استفاده از پایستگی انرژی در شاره در حال حرکت به دست آمده است. در ادامه با استفاده از پایستگی انرژی معادله برنولی را به دست خواهیم آورد.

اثبات معادله برنولی

مطابق با تصویر زیر، سیالی (در اینجا آب) را در نظر بگیرید که از سمت چپ به سمت راستِ لوله‌ای با مساحت و ارتفاع متغیر جریان دارد. همان‌گونه که گفته شد، آب به هنگام رسیدن به قسمتی از لوله با قطر باریک‌تر با سرعت بیشتری حرکت می‌کند و در نتیجه انرژی جنبشی به دست می‌آورد. مطابق با تصویر، از آنجایی که آب به ارتفاع بالاتری از لوله می‌رود بنابراین علاوه بر انرژی جنبشی، انرژی پتانسیل گرانشی نیز به دست خواهد آورد. معادله برنولی با استفاده از تساوی زیر به دست می‌آید.

انرژی به دست آمده توسط آب = کار خارجی انجام شده بر روی آب

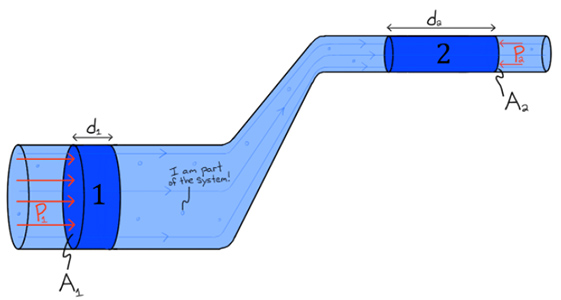
فرض کنید انرژی سیستم در نظر گرفته شده از حجم‌های ۱ و ۲ و همچنین کل آب بین این دو حجم تشکیل شده است. اگر جریان آب آرام باشد و مقدار نیروی اتلافی موثر بر جریان آب برابر صفر باشد، آنگاه مقدار انرژی اضافه‌ شده به سیستم به دلیل کار خارجی است که توسط نیروهای فشاریِ شاره اطراف بر محیط مورد نظر وارد می‌شود. بنابراین داریم:

$$W_{external} =\triangle  (K+U)_{system}$$

در ابتدا تلاش می‌کنیم کار خارجی انجام شده بر آب را به دست آوریم. از آنجایی که آب قرار گرفته بین ناحیه ۱ و ۲ جزئی از سیستم مورد نظر ما است در نتیجه، منشا کار خارجی انجام شده بر سیستم از ناحیه دیگری خواهد بود. تنها فشارهایی که می‌توانند به صورت مستقیم بر روی سیستم موردنظر، کار خارجی انجام دهند فشارهای $$P_1$$ و $$P_2$$ خواهند بود (تصویر نشان داده شده در بالا). اگر جهت حرکت آب (به سمت راست) را جهت مثبت در نظر بگیریم، کار انجام شده از طرف فشار $$P_1$$ بر روی حجم $$V_1$$ مثبت خواهد بود. اما فشار $$P_2$$ بر روی حجم $$V_2$$ کار منفی انجام می‌دهد.

همان‌طور که می‌دانیم اگر نیروی F بر جسمی وارد شود و آن را با اندازه مسافت d جابجا کند، کار انجام شده توسط این نیرو به صورت زیر نوشته می‌شود.

$$W=F d$$

اکنون اگر بر سطحی به مساحت A فشار P وارد شود، نیروی ناشی از این فشار برابر با $$F=P A$$ خواهد بود. در نتیجه برای کار انجام شده از طرف فشارهای $$P_1$$ و $$P_2$$ داریم:

$$W_1=P_1 A_1 d_1 \\ W_2=-P_2 A_2 d_2 $$

بنابراین کار خارجی انجام شده بر روی سیستم مورد نظر برابر است با:

$$W_{external}=P_1 A_1 d_1 - P_2 A_2 d_2 $$

همان‌گونه که در مطالب بالا اشاره شد، کار خارجی انجام شده بر سیستم برابر با انرژی اضافه شده به سیستم است، بنابراین داریم:

رابطه (۱)

$$W_{external}=P_1 A_1 d_1 - P_2 A_2 d_2 = \triangle (K+U)_{system}$$

از آنجایی که حجم یکسانی از آب از نقاط ۱ و ۲ عبور می‌کند در نتیجه داریم:

$$V_1= A_1 d_1 = A_2 d_2 = V_2 = V $$

با جایگذاری معادله بالا در رابطه (۱) خواهیم داشت:

رابطه (۲)

$$P_1 V - P_2 V = \triangle (K+U)_{system} $$

پس از ساده‌سازی سمت چپ رابطه (۱)، سمت راست رابطه را در نظر می‌گیریم. همان‌طور که در مطالب بالا گفته شد سیستم مورد نظر نه تنها حجم‌های ۱ و ۲، بلکه کل حجم آب مورد نظر بین این دو ناحیه را نیز در بر خواهد گرفت. بنابراین به دست آوردن انرژی این سیستم کمی پیچیده خواهد بود. در نتیجه، به منظور به دست آوردن معادله برنولی، فرضیه دیگری را در نظر می‌گیریم.

جریان شاره (در اینجا آب) را ثابت در نظر خواهیم گرفت. در این صورت، آب از نقطه‌ مشخصی در لوله با سرعت ثابتی عبور خواهد کرد. اکنون سوالی که مطرح می‌شود آن است که در نظر گرفتن آب با جریان ثابت چه کمکی برای به دست آوردن تغییرات انرژی برای سیستم پیچیده مورد نظر می‌کند. به منظور پاسخ به این پرسش تصویر زیر را در نظر بگیرید.

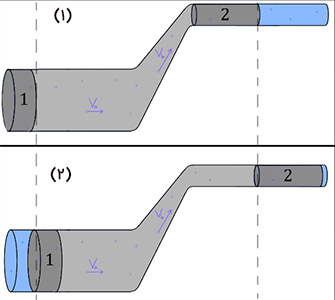
در تصویر بالا، سیستم مورد مطالعه با خاکستری نشان داده شده است. این سیستم از ناحیه‌های ۱، ۲ و کل آب محصور بین این دو ناحیه تشکیل می‌شود. در تصویر (۱)،‌ سیستم دارای انرژی کل $$(K+U)_{initial}$$ است. در تصویر (۲) کار خارجی بر روی کل سیستم انجام می‌شود. بنابراین، سیستم با به دست آوردن انرژی به سمت راست جابجا شده است. در نتیجه، انرژی کل سیستم به مقدار $$(K+U)_{final}$$ تغییر یافته است. از آنجایی که جریان آب را ثابت در نظر گرفتیم، انرژی آب محصور بین دو ناحیه ۱ و ۲ تغییر نخواهد کرد. در حقیقت، با در نظر گرفتن انرژی‌های نقاط پایانی، به سادگی می‌توان تغییر در انرژی کل سیستم را به دست آورد. برای تغییرات انرژی سیستم داریم:

$$\triangle(K+U)_{system} = (K_2+U_2)-(K_1+U_1)$$

با قرار دادن رابطه بالا در سمت راست رابطه (۲) خواهیم داشت:

$$P_1V-P_2V = (K_2+U_2)-(K_1+U_1)$$

با جایگزین کردن مقدار انرژی جنبشی ($$\frac{1}{2}mv^2$$) و انرژی پتانسیل ($$U_g= mgh$$) در رابطه بالا داریم:

رابطه (۳)

$$P_1V-P_2V = (\frac{1}{2}m_2v_2^2 -m_2g h_2 ) - (\frac{1}{2}m_1v_1^2 -m_1g h_1)$$

در رابطه به دست آمده $$P_1$$ و $$P_2$$ به ترتیب بیان‌گر فشارهای شاره در حجم‌های ۱ و ۲ هستند. همچنین مقادیر $$v_1$$ و $$v_2$$ به ترتیب نشان‌دهنده سرعت‌های شاره در حجم‌های ۱ و ۲ خواهند بود. ارتفاع شاره در حجم‌های $$v_1$$ و $$v_2$$ نیز به ترتیب با $$h_1$$ و $$h_2$$ نشان داده می‌شوند.

از آنجایی که فرض کردیم شاره در حال حرکت تراکم‌ناپذیر است، در نتیجه جرم‌های جابجا شده از حجم‌های ۱ و ۲ برابر خواهند بود. بنابراین داریم:

$$m_1 = m_2 = m$$

با برابر بودن جرم‌ها، رابطه (۳) به صورت زیر نوشته خواهد شد:

$$P_1-P_2 = \frac{\frac{1}{2}mv_2^2 }{V}+\frac{mg h_2}{V} - \frac{\frac{1}{2}mv_1^2}{V}-\frac{mg h_1}{V}$$

با توجه به تعریف چگالی به صورت $$\rho=\frac{m}{V}$$ داریم:

$$P_1-P_2 = {\frac{1}{2}\rho v_2^2 }+{\rho g h_2} - {\frac{1}{2}\rho v_1^2 }-{\rho g h_1}$$

با مرتب‌سازی رابطه به دست آمده در بالا خواهیم داشت:

$$P_1+{\frac{1}{2}\rho v_1^2 }+{\rho g h_1} = P_2 + {\frac{1}{2}\rho v_2^2 }+{\rho g h_2}$$

اکنون به معادله برنولی رسیدیم. این معادله می‌تواند به عنوان قانون پایستگی انرژی برای شاره در حال حرکت دیده شود. از آنجایی که $$P+{\frac{1}{2}\rho v^2 }+{\rho g h}$$ ‌در هر نقطه‌ای در مسیر جریان یکسان است، معادله برنولی به صورت زیر نیز نوشته می‌شود:

$$P+{\frac{1}{2}\rho v^2 }+{\rho g h} = constant$$

مقدار این ثابت برای شاره‌های مختلف متفاوت خواهد بود اما برای شاره‌ای با جریان ثابت و بدون نیرو‌های اتلافی، در هر نقطه‌ای ثابت است.

رابطه بین اصل برنولی و معادله برنولی

توجه به این نکته مهم است که اصل برنولی در معادله برنولی نهفته است. اگر رابطه زیر را در نظر بگیریم:

$$P_1+{\frac{1}{2}\rho v_1^2 }+{\rho g h_1} = P_2 + {\frac{1}{2}\rho v_2^2 }+{\rho g h_2}$$

و فرض کنیم که ارتفاع شاره تغییر نخواهد کرد، مقدار $$\rho g h$$ از طرفین رابطه بالا حذف می‌شود. بنابراین داریم:

$$P+{\frac{1}{2}\rho v^2 } = constant$$

رابطه به دست آمده بیان‌گر اصل برنولی خواهد بود. ثابت بودن رابطه بالا به این موضوع اشاره می‌کند که اگر سرعت شاره‌ در ناحیه مشخصی بزرگ‌تر باشد، فشار آن ناحیه کوچک‌تر خواهد بود (اصل برنولی). افزایش سرعت جریان شاره باید همراه با کاهش فشار باشد.

مثال اول معادله برنولی

فرض کنید به عنوان صاحب رستوران به دنبال راه‌های جدید برای تحویل نوشابه به مشتری هستید. به عنوان یک راهکار می‌توانید از لوله‌ای برای انتقال نوشابه به مشتری‌های رستوران استفاده کنید. بخشی از لوله در تصویر زیر نشان داده شده است. سرعت و فشار نوشابه را در نقطه ۱ به ترتیب برابر $$3.00 \frac{m}{s}$$ و $$12300 \ Pa$$ در نظر بگیرید. نقطه ۲ نسبت به نقطه ۱ به اندازه $$1.20$$ در ارتفاع بلندتری قرار گرفته است. همچنین سرعت جریان نوشابه در نقطه ۲ برابر $$0.750 \frac{m}{s}$$ خواهد بود. با استفاده از معادله برنولی فشار نوشابه را در نقطه 2 به دست آورید.

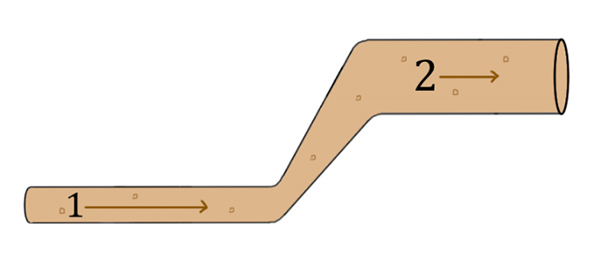
پاسخ:

معادله برنولی به صورت زیر نوشته می‌شود:

$$P_1+{\frac{1}{2}\rho v_1^2 }+{\rho g h_1} = P_2 + {\frac{1}{2}\rho v_2^2 }+{\rho g h_2}$$

رابطه بالا را بر حسب فشار در نقطه ۲ مرتب می‌کنیم:

$$P_2= P_1 + {\frac{1}{2}\rho v_1^2 }+{\rho g h_1}-{\frac{1}{2}\rho v_2^2 }-{\rho g h_2}$$

از آنجایی که نقطه ۱ در ارتفاع کمتری نسبت به نقطه ۲ قرار دارد، خط مرجع را خط افقی که از نقطه ۱ می‌گذرد در نظر می‌گیریم. در نتیجه داریم:

$$h_1 = 0 \\ h_2 = 1.2 \ m$$

با قرار دادن مقادیر بالا و داده‌های پرسش در رابطه برنولی داریم:

$$P_2 = 12300\ Pa \ + \frac{1}{2}(1090 \ \frac{kg}{m^3}) (3.00 \ \frac{m}{s})^2 - \frac{1}{2}(1090 \ \frac{kg}{m^3}) (0.750 \ \frac{m}{s})^2 - (1090 \ \frac{kg}{m^3})g (1.20 \ m) $$

در نتیجه مقدار فشار در ناحیه ۲ برابر $$4080 \ Pa$$ به دست خواهد آمد.

مثال دوم معادله برنولی

هتلی برای اتمام ساخت، قصد ساختن فواره‌ای را در محوطه بیرونی هتل دارد. برای تامین آب مورد نیاز برای این فواره از لوله‌ای استوانه‌ای با قطر 15 سانتی‌متر استفاده شده است. این لوله به صورت افقی در ۸ متر زیر زمین قرار گرفته است. آب پس از طی مسیری به صورت افقی در لوله، برای انتقال به سطح زمین از داخل لوله عمودی به قطر ۵ سانتی‌متر عبور خواهد کرد. انتهای لوله عمودی در ارتفاع 1/75 سانتی‌متری از سطح زمین قرار دارد و آب با سرعت 32/0 متر بر ثانیه از آن خارج می‌شود. مقدار فشار آب در لوله افقی را به دست آورید. ( چگالی آب را $$1000\ \frac{kg}{m^3}$$ در نظر بگیرید).

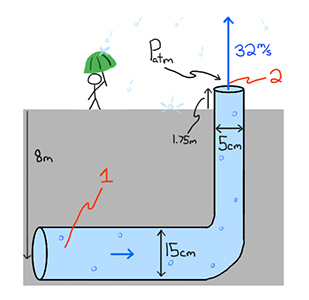
پاسخ:

نقطه ۱ را در نزدیکی ته لوله (بخش افقی) در نظر می‌گیریم. نقطه ۲ را بخش بالایی لوله عمودی و محل خروج آب قرار می‌دهیم. معادله برنولی را بر حسب فشار در نقطه ۱ مرتب می‌کنیم.

$$P_1=P_2+ {\frac{1}{2}\rho v_2^2 }+{\rho g h_2}-{\frac{1}{2}\rho v_1^2 }-{\rho g h_1}$$

سرعت آب در نقطه ۱ مجهول است. بنابراین، در ابتدا $$v_1$$ را به دست می‌آوریم. برای به دست آوردن این سرعت از معادله پیوستگی استفاده می‌کنیم.

$$A_1v_1 = A_2v_2$$

از آنجایی که لوله استوانه‌ای است، سطح مقطع آن به صورت زیر به دست خواهد آمد:

$$A=\pi r^2$$

با جایگزینی فرمول بالا در معادله پیوستگی داریم:

$$(\pi r_1^2)v_1 = (\pi r_2^2)v_2 $$

معادله بالا را بر حسب $$v_1$$ مرتب می‌کنیم:

$$v_1 = (\frac{r_2^2}{r_1^2})v_2$$

با جایگذاری مقادیر داده شده برای قطر لوله در بخش عمودی و افقی، مقدار $$v_1$$ به صورت زیر محاسبه می‌شود:

$$v_1 = \frac{(2.50\ cm)^2}{(7.50 \ cm)^2} (32.0 \frac{m}{s}) = 3.56\ \frac{m}{s} $$

اکنون با داشتن مقدار $$v_1$$، فشار در نقطه ۱ به صورت زیر به دست خواهد آمد:

$$P_1=P_2+\frac{1}{2}\rho(32 \ \frac{m}{s})^2+\rho gh_2- \frac{1}{2}\rho(3.56 \ \frac{m}{s})^2-\rho g h_1$$

نقطه ۱ را نقطه مرجع در نظر می‌گیریم، بنابراین ارتفاع $$h_1$$ برابر صفر است. ارتفاع در نقطه ۲ به صورت زیر به دست خواهد آمد:

$$h_2=8.00 \ m +1.75 \ m = 9.75 \ m$$

با قرار دادن مقادیر به دست آمده برای ارتفاع در دو نقطه ۱ و ۲ در رابطه بالا داریم:

$$P_1=P_2+\frac{1}{2}\rho(32 \ \frac{m}{s})^2+\rho g(9.75 \ m)- \frac{1}{2}\rho(3.56 \ \frac{m}{s})^2$$

با به دست آوردن فشار در نقطه ۲، فشار در نقطه ۱ به دست می‌آید. از آنجایی که نقطه ۲ (محل خروج آب) در تماس با هوا قرار دارد، در نتیجه فشار در این نقطه برابر با فشار جو خواهد بود. در معادله برنولی می‌توان از دو نوع فشار استفاده کرد.

1. فشار مطلق: در این صورت مقدار $$P_2$$ برابر $$1.01\ \times 10^5 \ Pa$$ خواهد بود.
2. فشار سنج: در این حال مقدار فشار در نقطه ۲ برابر صفر است.

برای راحتی کار فشار مطلق را انتخاب می‌کنیم و در معادله برنولی مقدار فشار در نقطه ۲ را برابر صفر قرار می‌دهیم. بنابراین داریم:

$$P_1=\frac{1}{2}\rho \ (32\ \frac{m}{s})^2+\rho g (9.75 \ m)-\frac{1}{2}\rho \ (3.56\ \frac{m}{s})^2$$

با قرار دادن مقدار چگالی آب ($$1000 \ \frac{kg}{m^3}$$) و شتاب جاذبه زمین ($$g=+\ 9.8 \ \frac{m}{s^2}$$) در معادله بالا خواهیم داشت:

$$P_1=\frac{1}{2} (1000\ \frac{kg}{m^3}) \ (32\ \frac{m}{s})^2+(1000\ \frac{kg}{m^3}) (+\ 9.8 \ \frac{m}{s^2}) (9.75 \ m)-\frac{1}{2} (1000\ \frac{kg}{m^3}) \ (3.56\ \frac{m}{s})^2$$

در نتیجه فشار در نقطه ۱ به صورت زیر به دست خواهد آمد:

$$P_1 = 6.01 \ \times 10^5 \ Pa$$

مثال سوم معادله برنولی

آب در لوله‌ای افقی با سطح مقطع $$4\ m^2$$ در نقطه A با سرعت $$5 \ \frac{m}{s}$$ و فشار $$300000 \ Pa$$ در جریان است. اگر سطح مقطع لوله در نقطه B برابر $$2\ m^2$$ باشد، مقدارهای زیر را به دست اورید:

1. سرعت جریان آب در نقطه B.
2. فشار در نقطه B.

پاسخ:

قسمت (۱): همان‌گونه که در تصویر زیر نشان داده شده است آب در لوله‌ای با سطح مقطع متغیر در جریان است.

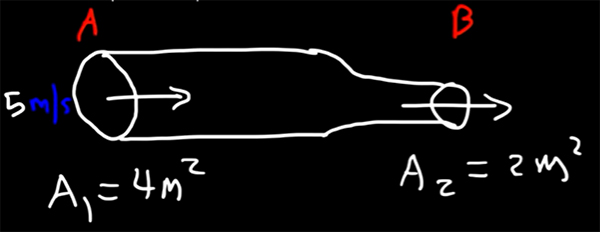
طبق معادله پیوستگی، با کاهش سطح مقطع لوله، سرعت جریان آب افزایش خواهد یافت. در نتیجه داریم:

$$A_1v_1 = A_2v_2 \\ (4 \ m^2)(5\ \frac{m}{s}) = (2 \ m^2) v_2 \\ v_2 = 10 \ \frac{m}{s}$$

قسمت (۲): طبق اصل برنولی هنگامی که فشار بالا باشد سرعت جریان شاره کم، و برعکس هنگامی که فشار پایین باشد،‌ سرعت جریان شاره زیاد خواهد بود. از آنجایی که آب در نقطه B با سرعت بیشتری حرکت می‌کند، در نتیجه فشار در نقطه B در مقایسه با فشار در نقطه A کمتر خواهد بود. در واقع، جریان آب از نقطه A به نقطه B با شتاب همراه است. عامل ایجاد کننده این شتاب، نیروی F است. به منظور محاسبه فشار در نقطه B از معادله برنولی استفاده می‌کنیم.

$$P_1+{\frac{1}{2}\rho v_1^2 }+{\rho g h_1} = P_2 + {\frac{1}{2}\rho v_2^2 }+{\rho g h_2}$$

از آنجایی که ارتفاع لوله ثابت است، $$\rho hg$$ از دو طرف معادله بالا حذف خواهد شد. با جایگذاری داده‌های مساله در رابطه بالا خواهیم داشت:

$$300000 \ Pa+{\frac{1}{2} (1000 \frac{kg}{m^3}) (5 \ \frac{m}{s})^2 }= P_2 + {\frac{1}{2} (1000 \frac{kg}{m^3}) (10 \ \frac{m}{s})^2 } \\ P_2 = 2925000 \ Pa$$

مثال چهارم معادله برنولی

با توجه به تصویر نشان داده شده در زیر،‌ سرعت و فشار آب را در نقطه‌های ‌‌‌B و C محاسبه کنید.

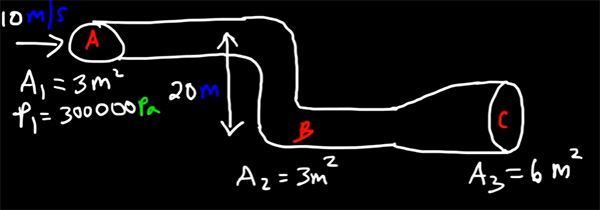
پاسخ: در ابتدا سرعت جریان آب در در نقطه‌های مختلف در نظر می‌گیریم. با توجه به آن‌که سطح مقطع لوله در دو نقطه A و B یکسان است، در نتیجه، سرعت جریان آب در نقطه B برابر با نقطه A خواهد بود.

$$v_A = v_B = 10 \ \frac{m}{s}$$

اکنون جریان آب از نقطه B به C را در نظر می‌گیریم. آز آنجایی که سطح مقطع لوله در نقطه C نسبت به نقطه B دو برابر شده است، بنابراین، سرعت جریان آب در نقطه C کاهش می‌یابد.

$$A_2v_2 = A_3v_3 \\ (3 \ m^2) (10 \ \frac{m}{s}) = (6 \ m^2)v_3 \\ v_3 = 5 \ \frac{m}{s}$$

می‌دانیم اگر ارتفاع افزایش یابد، فشار کاهش خواهد یافت. در نتیجه، فشار در نقطه‌ ‌‌B از فشار در نقطه A بیشتر خواهد بود. اکنون نقطه ‌C را در نظر می‌گیریم. در مثال سوم دیدیم، با افزایش سرعت شاره در یک نقطه، فشار در آن نقطه کاهش می‌یابد. در نتیجه داریم:

$$P_C> P_B > P_A$$

برای محاسبه فشار در نقطه B و C از معادله برنولی استفاده می‌کنیم (ارتفاع نقطه‌های B و C را صفر در نظر می‌گیریم) :

$$P_1+{\frac{1}{2}\rho v_1^2 }+{\rho g h_1} = P_2 + {\frac{1}{2}\rho v_2^2 }+{\rho g h_2}$$

با جایگذاری داده‌های پرسش در معادله برنولی داریم ( ذکر این نکته مهم است که سرعت در دو نقطه A و B با هم برابر و ارتفاع نقطه B برابر صفر است):

$$300000 \ Pa+{(1000 \ \frac{kg}{m^3})(9.8 \ \frac{m}{s^2}) (20 \ m)} = P_2 \\ P_2 = 496000 \ Pa$$

فشار در نقطه C به صورت زیر به دست خواهد آمد:

$$P_1+{\frac{1}{2}\rho v_1^2 }+{\rho g h_1}= P_3 + {\frac{1}{2}\rho v_3^2 }+{\rho g h_3} \\ 300000 \ Pa+{\frac{1}{2}(1000 \frac{kg}{m^3}) (10 \frac{m}{s})^2 }+{(1000 \frac{kg}{m^3}) (9.8 \ \frac{m}{s^2}) ( 20 \ m)}= P_3 + {\frac{1}{2}(1000 \frac{kg}{m^3}) (5 \frac{m}{s})^2 }+{(1000 \frac{kg}{m^3}) (9.8 \ \frac{m}{s^2}) ( 0)} \\ P_3 = 533500 \ Pa$$

معرفی فیلم آموزش فیزیک پایه دهم

مجموعه فرادرس در تولید و محتوای آموزشی خود اقدام به تهیه فیلم آموزش فیزیک پایه دهم برای دانش‌آموزان مقطع دهم کرده که این مجموعه آموزشی از پنج درس تشکیل شده است.

در درس یکم مبحث اندازه‌گیری تدریس می‌شود. در این درس دانش‌آموز با انواع وسیله‌های اندازه‌گیری و خطاهای آن‌ها آشنا خواهد شد و در انتها مفهوم چگالی را یاد می‌گیرد. دانش‌آموز در درس دوم، حالت‌های ماده، ویژگی‌های فیزیکی مواد در مقیاس نانو، نیروهای بین مولکولی، فشار در شاره‌ها، فشار و اصل ارشمیدس و شاره در حرکت و اصل برنولی را می‌آموزد. بنابراین، به منظور آشنایی بیشتر با اصل برنولی دیدن درس دوم این فیلم آموزشی توصیه می‌شود.

همان‌گونه که در مباحث بالاتر دیده شد به منظور به دست آوردن معادله برنولی، آشنایی با مبحث پایستگی انرژی بسیار ضروری خواهد بود. در نتیجه، مباحث مربوط به کار انجام شده توسط نیروی ثابت، کار و انرژی جنبشی، کار و انرژی پتانسیل و پایستگی انرژی پتانسیل در درس سوم آموزش داده می‌شود. در پایان، در درس‌های چهارم و پنجم مباحث مربوط به ترمودیناک تدریس می‌شود.

• برای دیدن فیلم آموزش فیزیک پایه دهم + اینجا کلیک کنید. 

کاربرد اصل برنولی چیست؟

بسیاری از مشاهدات در زندگی روزمره با استفاده از اصل برنولی توضیح داده می‌شوند. در ادامه کاربردهای اصل برنولی بررسی می‌شود.

بال هواپیما

قسمتی از بال هواپیما و خط‌های جریان هوا در تصویر زیر نشان داده شده است. جهت‌گیری بال نسبت به جهت جریان سبب نزدیک شدن خطوط جریان در بالایِ بالِ هواپیما خواهد شد. در نتیجه، سرعت در این قسمت، افزایش و فشار کاهش خواهد یافت. اما در قسمت پایینی بال هواپیما، فشار با فشار جو برابر است. از این رو، نیروی بالا‌بر در قسمت پایینی بال از نیروی پایین‌بر در قسمت بالایی بال، بزرگ‌تر خواهد بود. بنابراین، نیروی خالصی به سمت بالا خواهیم داشت.

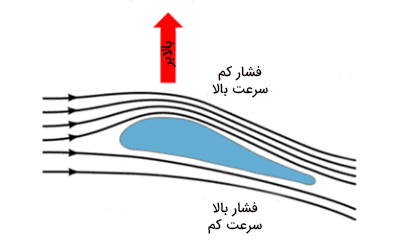
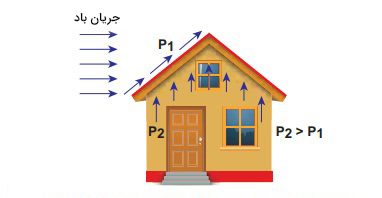
بلند شدن سقف خانه‌ها

گاهی مشاهده می‌کنید که به هنگام طوفان، سقف‌ کلبه‌ها بدون آسیب زدن به بقیه قسمت‌های کلبه از جا بلند خواهد شد. وزش باد فشار کمِ $$P_1$$ را بالای سقف کلبه ایجاد می‌کند. فشار $$P_2$$ در زیر سقف از فشار ایجاد شده توسط باد بیشتر است. در نتیجه، سقف کلبه به دلیل اختلاف فشار ایجاد شده از جا کنده خواهد شد.

چراغ بونزن

دوره دبیرستان با چراغ بونزن در آزمایشگاه شیمی یا فیزیک کار کرده‌اید.

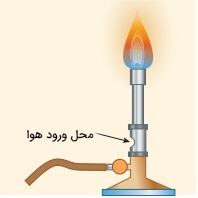
در چراغ بونزن، گاز با سرعت بالایی از نازل خارج می‌شود. در نتیجه، فشار داخل کاهش خواهد یافت. از این رو، هوای بیرون، از طریق حفره ورودِ هوا& به سمت مشعل می‌رود و ترکیب هوا و گاز موجب روشن شدن چراغ خواهد شد.

ونتوری‌متر

به منظور اندازه‌گیری سرعت جریان شاره‌ای تراکم‌ناپذیر از ونتوری‌متر استفاده می‌شود. اساس کار این وسیله براساس اصل برنولی است. در این وسیله دو لوله A و $$A^{'} $$ (با سطح مقطع یکسان A) توسط لوله باریک‌تر B (با سطح مقطع a) به هم متصل شده‌اند. مانومتر U شکلی نیز بین لوله‌های پهن‌تر و باریک‌تر قرار گرفته است (تصویر نشان داده شده در ادامه)

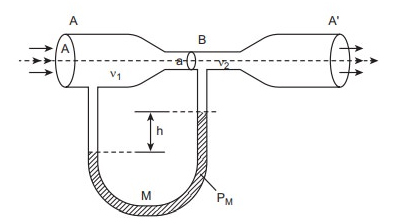
فرض کنید $$P_1$$ فشار شاره در ناحیه پهن‌تر لوله ‌A است. شاره‌ ای با چگالی $$\rho$$ را در نظر بگیرید که با سرعت $$v_1$$ در ناحیه پهن‌تر لوله جریان دارد. سرعت این شاره به هنگام عبور از ناحیه باریک‌تر به مقدار $$v_2$$ افزایش می‌یابد. طبق اصل برنولی، فشار شاره ($$P_2$$) در ناحیه باریک‌تر لوله B کاهش خواهد یافت. بنابراین، تفاوت فشار در لوله‌های ‌A و B به صورت اختلاف ارتفاعِ سطح مایع مانومتر نشان داده می‌شود.

با توجه به معادله پیوستگی داریم:

$$A_1v_1=A_2v_2 \\ v_2 = \frac{A}{a} v_1$$

با جایگزینی رابطه به دست آمده برای سرعت در معادله برنولی داریم:

$$P_1+ \rho\frac{v_1^2}{2}=P_2 \ + \rho\frac{1}{2}(\frac{A}{a}v_1)^2$$

 در نتیجه اختلاف فشار بین دو نقطه ۱ و ۲ به صورت زیر به دست خواهد آمد:

$$\triangle P=P_1-P_2 = \rho \frac{v_1^2}{2}\frac{(A^2-a^2)}{a^2}$$

سرعت شاره در انتهای لوله A (قسمت اتصالی به لوله باریک‌تر)به صورت زیر به دست می‌آید.

$$v_1^2=\frac{2(\triangle P) a^2}{\rho (A^2-a^2)} \ \Rightarrow v_1 = \sqrt{\frac{2(\triangle P) a^2}{\rho(A^2-a^2)}}$$

در پایان، حجم شاره در حال حرکت بر حسب ثانیه برابر است با:

$$V=A v_1 = aA\sqrt{\frac{2(\triangle P) }{\rho(A^2-a^2)}}$$

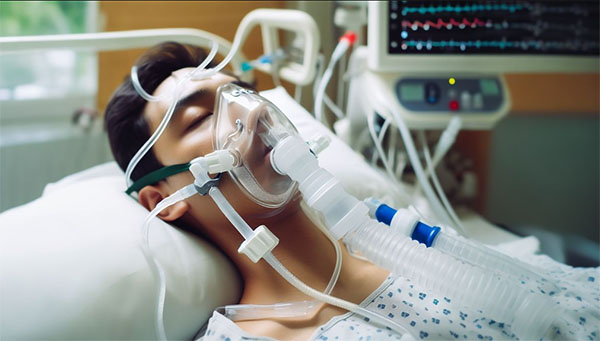
کاربرد اصل برنولی در پزشکی

یکی از کاربردهای اصل برنولی در پزشکی استفاده از آن در ماسک ونتوری است. ماسک ونتوری نوعی ماسک اکسیژن پزشکی است که غلظتی از اکسیژن را به بیماران تحت کنترل منتقل می‌کند. لوله‌ای ماسک را به نازلِ متصل به کپسول اکسیژن وصل کرده است. لوله دارای حفره کوچکی است که هوای اتاق از طریق آن به داخل ماسک می‌رود. ماسک ونتوری مقدار اکسیژن موجود در هوای اتاق را همراه با مقدار اکسیژن ورودی از طریق نازل به ماسک، کنترل می‌کند. جریان اکسیژن به داخل لوله سبب کاهش فشار می‌شود. این کاهش فشار اجازه می‌دهد هوا به درون ماسک جریان پیدا کند و با اکسیژن ورودی از طریق نازل مخلوط شود.

آزمایش های جالب در مورد اصل برنولی

برای درک بهتر اصل برنولی در ادامه دو آزمایش ساده و جالب مطرح می‌شود.

آزمایش 1

برای مشاهده اصل برنولی به صورت عملی می‌توانید آزمایش ساده زیر را در منزل انجام دهید.

وسایل مورد نیاز:

1. سشوار
2. توپ کوچک پلاستیکی

سشوار را روشن کنید و به صورت عمودی نگه دارید. در ادامه، توپ پلاستیکی کوچک را در جریان هوای سشوار به حال تعادل درآورید. ملاحظه می‌کنید تا هنگامی که سشوار روشن است توپ به حالت معلق باقی خواهد ماند.

بر طبق اصل برنولی، شاره‌ای که با سرعت بیشتری حرکت می‌کند دارای فشار کمتری است. با روشن کردن سشوار، جریان سریعی از هوا را ایجاد می‌کنیم. در نتیجه، از آنجایی که سرعت جریان هوا بالا است، فشار آن نسبت به فشار اطراف کمتر خواهد بود.

اگر توپ از مسیر جریان هوای خروجی از سشوار منحرف شود، با فشار بیشتری نسبت به فشار جریان هوای خروجی از سشوار روبرو خواهد شد. در نتیجه، فشار بیشتر محیط اطراف، توپ را به داخل جریان هوای خروجی از سشوار برمی‌گرداند.

آزمایش ۲

برای انجام این آزمایش ساده وسایل زیر را تهیه کنید:

• کاغذ
• نوار چسب
• نی
• توپ پینگ‌پنگ
• قیچی
• مداد

دایره‌ای به قطر ۱۰ سانتی‌متر بر روی کاغذ رسم کنید و به وسیله قیچی آن‌را ببرید. سپس به وسیله قیچی برشی به اندازه شعاع دایره در آن ایجاد کنید. در ادامه مخروطی به شکل زیر درست کنید.

سپس سر نی را به صورت عمودی خم کنید و مخروط ساخته شده را به وسیله چسب نواری به سر نی بچسبانید. نکته مهم آن است مخروط را طوری به وسیله چسب نواری به نی بچسبانید که راه خروجی هوا کاملا مسدود شده باشد. اکنون توپ پینگ‌پنگ را بر روی مخروط قرار دهید. از سر دیگر نی محکم در آن بدمید. ملاحظه می‌کنید که توپ پینگ‌پنگ در قسمت بالای مخروط به حالت معلق قرار می‌گیرد. دلیل این اتفاق در آزمایش ۱ توضیح داده شده است.

جمع‌بندی

در این مطلب با اصل برنولی آشنا شدید. بر طبق اصل برنولی، شاره‌ در حال حرکت با سرعت بالا دارای فشار کم است. همچنین، اگر شاره‌ای با سرعت کم حرکت کند دارای فشار زیاد خواهد بود. در ادامه، با استفاده از پایستگی انرژی معادله برنولی اثبات شد و با حل مثال‌های گوناگون با نحوه حل مساله با استفاده از معادله برنولی آشنا شدیم.