اسیلاتور کریستالی – به زبان ساده
در آموزشهای قبلی مجله فرادرس، درباره انواع اسیلاتورها بحث کردیم. در این آموزش قصد داریم به بررسی اسیلاتور کریستالی بپردازیم. یکی از مهمترین ویژگیهای همه اسیلاتورها، «پایداری فرکانسی» (Frequency Stability) یا به عبارت دیگر، قابلیت اسیلاتور در فراهم کردن فرکانس پایدار در خروجی و با شرایط بار متغیر است.

برخی از عوامل تاثیرگذار روی پایداری فرکانسی یک اسیلاتور به صورت کلی شامل موارد زیر است:
- تغییرات دمایی
- تغییرات بار
- تغییرات ولتاژ در منبع توان DC
با انتخاب مناسب عناصر مورد استفاده در مدار فیدبک تشدیدی مانند تقویتکننده، میتوان پایداری فرکانسی سیگنال خروجی را بهبود داد. اما در مدار تانک اسیلاتورهای LC و RC، برای پایداری فرکانسی قابل حصول محدودیتهایی وجود دارد.
اسیلاتور کریستالی کوارتز
برای رسیدن به سطوح بالای پایداری فرکانسی، لازم است که «کریستال کوارتز» (Quartz Crystal) وظیفه تشخیص فرکانس را به عهده بگیرد. به این ترتیب یک مدار نوسانساز به وجود میآید که به طور کلی آن را، «اسیلاتور کریستال کوارتز» (Quartz Crystal Oscillator) مینامند.
هنگامی که یک منبع ولتاژ به یک قطعه نازک از کریستال کوارتز اعمال میشود، شکل آن تغییر میکند. این خاصیت در کریستال، «اثر پیزو-الکتریک» (Piezo-Electric Effect) نام دارد. اثر پیزو-الکتریک، خاصیتی از کریستال است که در آن بار الکتریکی، با تغییر شکل کریستال نیروی مکانیکی ایجاد میکند. به صورت معکوس، نیروی مکانیکی وارد بر کریستال نیز میتواند بار الکتریکی تولید کند.
قطعات پیزو-الکتریک را میتوان در دسته ترانسدیوسرها قرار داد. این قطعات، یک نوع از انرژی را به نوع دیگری از انرژی (الکتریکی به مکانیکی و مکانیکی به الکتریکی) تبدیل میکنند. اثر پیزو-الکتریک، باعث ایجاد لرزشهای مکانیکی یا نوسان الکتریکی میشود که میتوان از آن به جای مدار تانک LC در اسیلاتورها استفاده کرد.
انواع مختلفی از مواد کریستالی وجود دارند که میتوان از آنها به عنوان اسیلاتور استفاده کرد. از معروفترین انواع این مواد کریستالی برای مدارهای الکترونیکی میتوان به ماده معدنی کوارتز به دلیل استحکام مکانیکی بالای آن اشاره کرد.
کریستال کوارتز مورد استفاده در اسیلاتور کریستال کوارتز، یک تیغه بسیار کوچک و باریک از کوارتز است که دو طرف آن، برشهای موازی دارد و به قطعات فلزی متصل میشود تا اتصالات الکتریکی مورد نیاز را ایجاد کند. ابعاد فیزیکی و ضخامت مورد نیاز برای این قطعه کریستال کوارتز با دقت خاصی کنترل میشود. زیرا این قطعه، فرکانس نهایی یا بنیادی نوسانها را تعیین میکند. فرکانس بنیادی در حالت کلی به نام «فرکانس مشخصه» (Characteristic Frequency) نیز شناخته میشود.
هنگامی که قطعه کریستالی به طور مناسب، بریده و شکل داده میشود، نمیتوان آن را در فرکانسهای دیگر به کار برد. به عبارت دیگر، ابعاد و شکل کریستال، تعیینکننده فرکانس بنیادی نوسانها در کریستال هستند.
مشخصات کریستال یا فرکانس مشخصه، با ضخامت فیزیکی کریستال بین دو صفحه فلزی به طور معکوس متناسب است. یک کریستال که به صورت مکانیکی، مرتعش میشود را میتوان با مدار الکتریکی معادل آن نشان داد. این مدار الکتریکی شامل مقاومت کوچک R، اندوکتانس بزرگ L و خازن کوچک C است. شکل زیر، مدار معادل کریستال کوارتز را نشان میدهد:
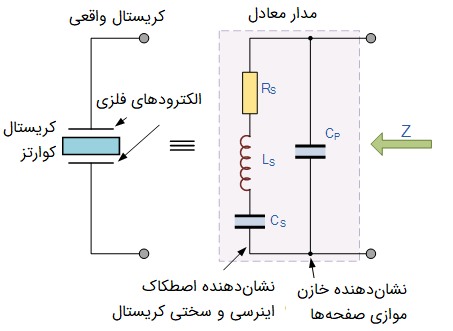
امپدانس معادل کریستال، شامل یک تشدید سری است. در این حالت، خازن با اندوکتانس در فرکانس کاری کریستال تشدید میکند. این فرکانس، با نام فرکانس سری کریستال یا شناخته میشود. همانند این فرکانس سری، یک فرکانس ثانویه نیز وجود دارد که در نتیجه تشدید موازی روی میدهد. این تشدید موازی بین المانهای سری و و خازن موازی روی میدهد.
شکل زیر، امپدانس خروجی اسیلاتور کریستالی را بر حسب فرکانس نشان میدهد:

اگر فرکانس نوسان اسیلاتور از نقطه تشدید سری مدار بزرگتر شود، اسیلاتور کریستالی تا رسیدن به نقطه فرکانس تشدید موازی ()، خاصیت سلفی خواهد داشت. در این نقطه از فرکانس، تعامل بین سلف سری () و خازن موازی یک مدار تانک LC تنظیمشده را به وجود میآورد. به همین دلیل، امپدانس در دو سر کریستال به حداکثر مقدار ممکن خود میرسد.
میتوان مشاهده کرد که اسیلاتور کریستالی از نوع کوارتز، ترکیبی از مدارهای تشدیدی تنظیمشده سری و موازی است. این اسیلاتور در دو فرکانس متفاوت، تولید سیگنالهای نوسانی میکند. بسته به نحوه برش کریستال، این دو فرکانس متفاوت ممکن است اختلاف ناچیزی داشته باشند. از آنجا که اسیلاتور کریستالی را نمیتوان همزمان برای دو فرکانس تنظیم کرد، لازم است که مدار اسیلاتور کریستال برای یک فرکانس مشخص تنظیم شود. زیرا کریستال فقط در یکی از فرکانسهای تشدید سری یا موازی از خود خاصیت نوسانی نشان میدهد.
بنابراین بسته به مشخصات مدار، یک کریستال کوارتز ممکن است به صورت یک خازن، سلف یا مدار تشدیدی سری یا مدار تشدیدی موازی کار کند. برای اینکه این مسئله واضح شود، میتوان راکتانس کریستال را بر حسب فرکانس رسم کرد. شکل زیر، راکتانس کریستال را بر حسب فرکانس نشان میدهد:

بنابراین رابطه فرکانس تشدید سری برای کریستال () به صورت زیر داده میشود:
فرکانس تشدید موازی برای کریستال () هنگامی رخ میدهد که راکتانس بازوی سری LC با راکتانس خازن موازی () برابر باشد. این فرکانس به صورت زیر داده میشود:
در ادامه با بیان چند مثال، اسیلاتور کریستالی را بیشتر مورد بررسی قرار میدهیم.
مثال
مدار یک اسیلاتور کریستالی المانهایی با مقادیر زیر دارد:
اگر خازن بین دو پایانه این کریستال () مقداری برابر داشته باشد، مقدار فرکانس بنیادی و فرکانس تشدید ثانویه کریستال را محاسبه کنید.
حل: فرکانس تشدید سری کریستال یا همان به صورت زیر محاسبه میشود:
فرکانس تشدید موازی کریستال یا نیز به صورت زیر محاسبه میشود:
میتوان مشاهده کرد که اختلاف بین فرکانس بنیادی کریستال () و بسیار کوچک و در حدود است.
هرچند در این محدوده فرکانسی، «ضریب کیفیت» (Quality Factor) کریستال عدد بسیار بزرگی است. زیرا اندوکتانس کریستال نسبت به مقادیر خازنی یا مقاومتی آن بسیار بزرگتر است. برای این مثال ضریب کیفیت اسیلاتور کریستالی در فرکانس تشدید سری، به صورت زیر داده میشود:
بزرگی ضریب کیفیت در این مثال (25000)، به دلیل نسبت بزرگ است. ضریب کیفیت بیشتر اسیلاتورهای کریستالی در محدوده 20000 تا 200000 است. اما ضریب کیفیت مدار تانک تنظیمشده در بهترین اسیلاتورهای LC، از عدد ۱۰۰۰ نیز بسیار کمتر است. عدد بزرگ ضریب کیفیت کریستال، نمایانگر پایداری فرکانسی بهتر کریستال در فرکانس کاری آن است. به دلیل پایداری فرکانسی بهتر، از این ماده معدنی برای ساخت مدارهای اسیلاتور کریستالی بسیار استفاده میشود.
مشاهده کردیم که کریستال کوارتز، فرکانس رزونانسی مشابه مدار تانک LC تنظیمشده دارد. با این تفاوت که ضریب کیفیت آن بسیار بزرگتر است. ضریب کیفیت بزرگتر، به دلیل مقاومت سری () کوچک اسیلاتور کریستالی رخ میدهد. در نتیجه، کریستال کوارتز انتخاب مناسبی برای استفاده در اسیلاتورهای فرکانس بالا است.
فرکانس نوسان تولید شده در اسیلاتورهای کریستالی، بسته به وضعیت مدار و تقویتکننده مورد استفاده، بازهای در حدود تا دارد. برش کریستال نیز در تعیین رفتار آن موثر است، زیرا بعضی کریستالها در بیشتر از یک فرکانس ارتعاش مکانیکی خواهند داشت. این مسئله منجر به تولید نوسانهای اضافی در اسیلاتور میشود که «اُوِرتون» (Overtone) نام دارد.
همچنین، اگر کریستال در طول دو صفحه موازی خود ضخامت موازی یا یکنواخت نداشته باشد، ممکن است دو یا چند فرکانس تشدید با فرکانس بنیادی داشته باشد که آن را هارمونیک مینامند. یعنی ممکن است اسیلاتور، هارمونیکهای دوم یا سوم داشته باشد.
به طور کلی، فرکانس نوسان بنیادی برای کریستال کوارتز، بسیار قویتر از فرکانس هارمونیکهای ثانویه آن است. بنابراین فرکانس کاری اسیلاتور کریستالی، همان فرکانس نوسان بنیادی آن است. همانطور که مشاهده شد، کریستالها یک مدار معادل دارند که شامل سه عنصر راکتیو یعنی دو خازن و یک سلف است. بنابراین دو فرکانس تشدید وجود دارد، فرکانس کمتر همان فرکانس تشدید سری و فرکانس تشدید بزرگتر، همان فرکانس تشدید موازی اسیلاتور است.
در آموزشهای قبلی مجله فرادرس مشاهده کردیم که اگر در یک تقویتکننده، بهره حلقه برابر یا بزرگتر از یک و فیدبک نیز مثبت باشد، مدار تقویتکننده نوسان خواهد کرد. در مدار اسیلاتور کریستال کوارتز، فرکانس نوسان اسیلاتور معادل فرکانس تشدید موازی بنیادی آن خواهد بود. زیرا با اعمال منبع ولتاژ، کریستال شروع به نوسان خواهد کرد.
هرچند میتوان یک اسیلاتور کریستالی را به گونهای تنظیم کرد که در هارمونیکهای زوج فرکانس بنیادی (دوم، چهارم، هشتم و ...) نوسان کند. به این ترتیب، این اسیلاتور را «اسیلاتور هارمونیک» (Harmonic Oscillator) مینامند. در حالیکه اسیلاتورهای اُوِرتن در مضارب فرد فرکانس بنیادی (سوم، پنجم، هفتم و ...) نوسان خواهند کرد. به طور کلی، در اسیلاتورهای کریستالی فرکانس اُوِرتن با فرکانس تشدید سری برابر است.
اسیلاتور کریستال کوارتز کولپیتس
مدارهای اسیلاتور کریستالی در حالت کلی، بر اساس ترانزیستورهای دوقطبی یا FET ساخته میشوند. زیرا اگرچه میتوان از تقویتکنندههای عملیاتی در مدارهای اسیلاتور با فرکانس پایینتر از نیز استفاده کرد، اما تقویتکنندههای عملیاتی پهنای باند لازم برای عملکرد در فرکانسهای بالاتر از را ندارند. در این بازه فرکانسی، از کریستال استفاده میشود.
طراحی اسیلاتور کریستالی به طراحی اسیلاتور کولپیتس که در قسمتهای قبل آن را مشاهده کردیم، بسیار نزدیک است. تفاوت در این است که مدار تانک LC که در فیدبک اسیلاتور باعث تولید نوسان میشود با کریستال کوارتز جایگزین شده است. شکل زیر، این مسئله را نشان میدهد:
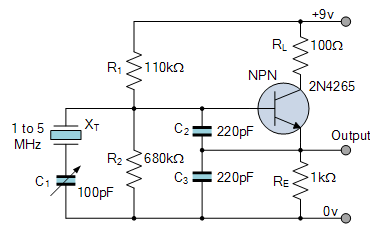
دیاگرام مداری نشان داده در شکل بالا، مدار اسیلاتور کریستالی کولپیتس را نشان میدهد. در این مدار، خازنهای و خازنهای بایپس هستند و خروجی ترانزیستور را حذف میکنند. به این ترتیب، سیگنال فیدبک کوچکتر میشود. بنابراین، از آنجا که میخواهیم بهره ترانزیستور را در مقدار معقولی نگه داریم، مقادیر و باید محدود شوند. برای جلوگیری از اتلاف توان اضافی در کریستال، دامنه خروجی باید تا حد امکان کوچک نگه داشته شود. در غیر این صورت، به دلیل نوسانهای زیاد، مدار کارایی خود را از دست خواهد داد.
اسیلاتور پیرس
یک طراحی معمول دیگر برای اسیلاتور کریستال کوارتز، «اسیلاتور پیرس» (Pierce Oscillator) است. طراحی اسیلاتور پیرس به اسیلاتور کولپیتس بسیار نزدیک است. این اسیلاتور، برای پیادهسازی مدار اسیلاتور کریستالی بسیار مناسب است. در این اسیلاتور، از یک کریستال به عنوان قسمتی از مدار فیدبک استفاده میشود.
اساسا اسیلاتور پیرس یک مدار تنظیمشده تشدیدی سری است که در قسمت تقویتکننده خود از JFET استفاده میکند. زیرا ترانزیستور FET امپدانس ورودی بسیار بزرگی دارد. شکل زیر، مدار اسیلاتور کریستالی پیرس را نشان میدهد:
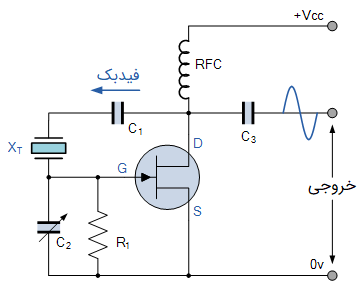
در حالی که ولتاژ دو سر چوک فرکانس رادیویی، در هر چرخه معکوس میشود، مقاومت مقدار فیدبک و تحریک کریستال را کنترل میکند. بیشتر ساعتها و تایمرهای دیجیتال، به نوعی از اسیلاتور پیرس استفاده میکنند. زیرا میتوان با کمترین تعداد قطعات مداری، این اسیلاتور را ساخت.
علاوه بر استفاده از ترانزیستور و FET در ساخت اسیلاتور کریستالی، میتوان از اینورتر CMOS به عنوان المان بهره در اسیلاتورهای کریستالی تشدیدی موازی استفاده کرد. یک اسیلاتور کریستالی کوارتز ساده از یک گیت منطقی اشمیت تریگر معکوسکننده یا CMOS، یک سلف کریستالی و دو خازن تشکیل میشود. این دو خازن مقدار ظرفیت خازنی بار کریستال را تعیین میکنند. مقاومت سری نیز به محدود کردن جریان تحریک کریستال کمک میکند و خروجی معکوسکننده را نسبت به امپدانس مختلط ایجاد شده توسط شبکه کریستال-خازنی عایق میکند.
شکل زیر، یک اسیلاتور کریستالی با CMOS را نشان میدهد:
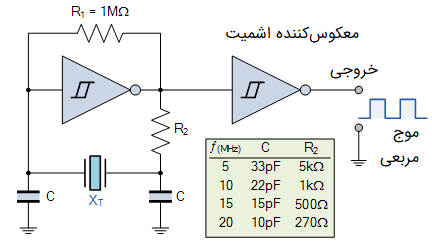
اینورتر، جابجایی فازی معادل ۱۸۰ درجه ایجاد میکند و شبکه خازنی کریستال، یک اختلاف فاز ۱۸۰ درجه دیگر ایجاد میکند که برای شروع نوسانها لازم است. مزیت اسیلاتور کریستالی CMOS، این است که میتواند خود را مجددا تنظیم کند تا به جابجایی فاز ۳۶۰ درجه لازم برای نوسان برسد.
بر خلاف اسیلاتورهای کریستالی قبلی که بر اساس ترانزیستور بودند و در خروجی خود شکل موج سینوسی ایجاد میکردند، اینورتر اسیلاتور CMOS از گیتهای منطقی دیجیتال استفاده میکند. به این ترتیب، خروجی این اسیلاتور به صورت موج مربعی خواهد بود که در محدوده دامنه حداکثر و دامنه حداقل نوسان میکند. به طور طبیعی، حداکثر فرکانس نوسان به مشخصات کلیدزنی گیت منطقی استفاده شده بستگی دارد.
کلاک ریز پردازنده با کریستال کوارتز
نمیتوان مبحث اسیلاتورهای کریستال کوارتز را بدون اشاره به ریزپردازندههای کلاک کریستالی پایان داد. به طور کلی همه ریزپردازندهها، میکروکنترلرها، PIC ها و CPU ها از اسیلاتور کریستال کوارتز در بخش تعیین فرکانس خود استفاده میکنند تا شکل موج کلاک مورد نظر را تولید کنند. زیرا میدانیم که اسیلاتورهای کریستالی، نسبت به اسیلاتورهای مقاومتی-خازنی (RC) و سلفی-خازنی (LC) بالاترین میزان دقت و پایداری فرکانسی را فراهم میکنند.
کلاک CPU موید این مطلب است که یک پردازنده با چه سرعتی میتواند کار کند و عملیات پردازش اطلاعات را با ریزپردازنده، PIC یا میکروکنترلر انجام دهد. سرعت کلاک برای این قطعات به این معنی است که این پردازنده میتواند در هر دوره تناوب کلاک، یک میلیون بار عملیات پردازش داخلی اطلاعات در ثانیه را انجام دهد. به طور کلی، تنها چیزی که یک ریزپردازنده برای تولید شکل موج کلاک نیاز دارد، یک کریستال و دو خازنی سرامیکی با مقادیری بین 15 تا 33 پیکوفاراد است. شکل زیر، یک اسیلاتور ریزپردازنده را نشان میدهد:
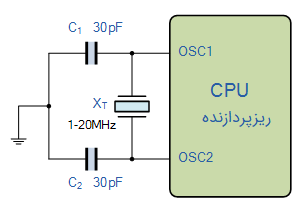
در ادامه با بیان یک مثال دیگر، اسیلاتور کریستال کوارتز را مورد بررسی بیشتر قرار میدهیم.
مثال
مدار معادل یک اسیلاتور کریستال کوارتز، پس از برش مقادیر زیر را دارد:
مقدار فرکانس نوسان سری و موازی کریستال را محاسبه کنید.
حل: فرکانس نوسان سری به صورت زیر محاسبه میشود:
فرکانس نوسان موازی به صورت زیر داده میشود:
بنابراین فرکانس نوسانها برای اسیلاتور کریستالی بین و خواهد بود.
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، پیشنهاد میکنیم به آموزشهای زیر مراجعه کنید:
- اسیلاتور LC — به زبان ساده
- اسیلاتور هارتلی — به زبان ساده
- اسیلاتور کولپیتس — به زبان ساده
- اسیلاتور RC — به زبان ساده
^^












سلام
میخواستم فرکانس ثابت تولید کنم برای راه اندازی التراسونیک بخور سرد که 110 کیلو هرتز رو بهم بده
با سلام و تشکر از مطالب عالیتون بنده تعمیر کار موبایل هستم یه سوال داشتم وقتی می خوایم یه کریستال رو عوض کنیم کریستال جایگزین باید کدوم یکی از شمارهاش با کریستال اصلی مثل هم باشه ممنون میشم اگه پاسخ بدید خیلی مهمه برام
سلام، ممنون از مطالب مفیدتون
من اسیلاتور موج مربعی با استفاده از کریستال و گیت نات بستم فرکانسش درست جواب میده ولی موجم مربعی نمیشه علتش چیه؟
ممنون میشم راهنماییم کنید
در جواب خانم فاطمه که پرسیدند چرا شکل موج مربعی نمیشه باید گفت که اگر فرکانس اسلاتوری که ساختید بیشتر از حد فرکانسی باشه که اسکوپتون میتونه تشخیص میده شکل موج دچار تغییر میشه…
چون هم پروبتون و هم مقاومت و خازن داخلی اسکوپ باعث فیلتر شدن بعضی از هارمونیکهای موج مربعی شما میشن