ممان اینرسی مستطیل – فرمول و محاسبه + مثال و حل تمرین
گشتاور دوم سطح مستطیل یا ممان اینرسی مستطیل، یکی از مشخصات هندسی مقطعهای مستطیلی شکل است که نحوه توزیع نقاط مختلف این شکل نسبت به یک محور مشخص نمایش میدهد. ممان اینرسی مستطیل، به طول و عرض آن بستگی دارد. این کمیت معمولا به منظور ارزیابی مقاومت خمشی و پیچشی اجسام دارای مقطع مستطیلی مورد استفاده قرار میگیرد. در این مقاله، به معرفی مفهوم و فرمول ممان اینرسی مقطع مستطیل (توپر، توخالی، جدار نازک، دوران یافته و مربع) میپردازیم. علاوه بر این، چند مثال متنوع و کاربردی را تشریح میکنیم.
- تعریف و نحوه تحلیل ممان اینرسی مستطیل را یاد میگیرید.
- فرمولهای اصلی ممان اینرسی مستطیل با در نظر گرفتن محور مرکزی «x» و «y» را میآموزید.
- یاد میگیرید چگونه ممان اینرسی مستطیل توپر و توخالی را محاسبه کنید.
- نقش ممان اینرسی در طراحی و تحلیل سازههای مهندسی را یاد خواهید گرفت.
- با کاربرد قضیه محورهای موازی برای انتقال محور و محاسبه ممان اینرسی آشنا میشوید.
- تفاوت ممان اینرسی و گشتاور دوم سطح را خواهید آموخت.
ممان اینرسی سطح چیست ؟
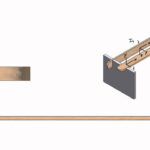
«گشتاور قطبی» (Polar Moment)، «گشتاور دوم سطح» (Second Moment of Area) یا «ممان اینرسی سطح» (Area Moment Of Inertia)، یکی از مشخصات مقطعهای دوبعدی است که نحوه پراکندگی نقاط مقطع، نسبت به یک محور مشخص را نمایش میدهد. این مشخصه، معمولا به منظور ارزیابی تغییر شکل اجسام تحت بارگذاری (مانند تیر در اسکلت ساختمان) مورد استفاده قرار میگیرد. برای درک مفهوم ممان اینرسی سطح یا ممان اینرسی مقطع، تیر چوبی نمایش داده شده در تصویر زیر را در نظر بگیرید.

مقاطع این تیر به شکل مستطیل هستند. تیر مستطیلی را به دو صورت زیر بر روی یک مسیر قرار میدهیم. در یکی از حالتها، عرض مقطع را به عنوان تکیهگاه تیر و در حالت دیگر، طول مقطع را به عنوان تکیهگاه تیر در نظر میگیریم.

اکنون، یک وزنه را بر روی تیر قرار میدهیم. همانطور که مشاهده میکنید، در یکی از حالتها، تیر به اندازه بیشتری خم میشود. دلیل این موضوع، تفاوت در ممان اینرسی مقطعها یا همان پراکندگی نقاط سطح مقطعها نسبت به محور عمود بر بارگذاری است. هر چه مقدار ممان اینرسی مقطع بیشتر باشد، مقاومت آن در برابر خمش بیشتر خواهد بود.

در مثال بالا، مقطعهای تحت بارگذاری به شکل زیر هستند. در مقطع سمت چپ، توزیع فاصله نقاط شکل نسبت به محور خمش، بیشتر از همین توزیع برای مقطع سمت راست است. بنابراین، با وجود برابر بودن ابعاد، مقطع سمت چپ، مقاومت بهتری در برابر خمش از خود به نمایش میگذارد.
در مهندسی سازه، تیرها معمولا با مقاطعی به شکل I یا H ساخته میشوند. این نوع مقاطع، مقاومت بسیار خوبی در برابر بارگذاری خمشی دارند. به طور کلی، مقطعهای دایرهای (توپر، توخالی، کامل، نیمدایره) و مستطیلی، بهترین مقاومت را در برابر خمش از خود به نمایش میگذارند. به همین دلیل، بسیاری از المانهای سازهای در مهندسی عمران با این مقطعها ساخته میشوند.
ممان اینرسی مقطع چگونه محاسبه می شود ؟
گشتاور دوم سطح، مجموع فاصله هر نقطه از مقطع دوبعدی یک جسم تا محور مبنا را نمایش میهد. به عنوان مثال، مقطع زیر را در نظر بگیرید. برای محاسبه ممان اینرسی این مقطع نسبت، باید فاصله هر یک از نقاط آن تا محور مبنا مورد نظر را به دست بیاوریم.
اگر محور x را به عنوان محور مبنا در نظر بگیریم، فاصله هر نقطه این محور برابر با y شده و فرمول محاسبه ممان اینرسی مقطع به صورت زیر نوشته میشود:
در صورت انتخاب محور y به عنوان محور مبنا، فرمول ممان اینرسی مقطع به صورت زیر تغییر میکند:
گشتاور دوم سطح، همواره مثبت است.
ممان اینرسی مستطیل چگونه بدست می آید ؟
برای یادگیری نحوه محاسبه ممان اینرسی مستطیل، مستطیلی به طول b و عرض h را بر روی دستگاه محورهای مختصات x-y در نظر بگیرید. محورهای x و y، از مرکز هندسی این مستطیل عبور میکنند. به عبارت دیگر، این محورها، مرکزی هستند.
با در نظر گرفتن محور مرکزی x به عنوان محور مبنای محاسبه ممان اینرسی، فرمول ممان اینرسی مستطیل از رابطه زیر به دست میآید:
در صورت انتخاب محور مرکزی y به عنوان محور مبنای محاسبه ممان اینرسی، فرمول ممان اینرسی مستطیل به صورت زیر نوشته میشود:
در هر یک از این فرمولها داریم:
- Ix: ممان اینرسی مستطیل نسبت به محور مرکزی x
- Iy: ممان اینرسی مستطیل نسبت به محور مرکزی y
- b: طول (قاعده) مستطیل
- h: عرض (ارتفاع) مستطیل
ممان اینرسی مقطع مستطیل چه کاربردی دارد ؟
گشتاور دوم سطح مستطیل، در بسیاری علوم مهندسی کاربرد دارد. به عنوان مثال، در مهندسی سازه، این پارامتر به طور گسترده برای محاسبه تغییر شکل تیر و تنشهای ناشی از اعمال گشتاور بر روی آن مورد استفاده قرار میگیرد. طراحی تیرهای بتنی، با مقطع مستطیل انجام میشوند. در مهندسی مکانیک نیز امکان طراحی المانهای مستطیلی تحت خمش وجود دارد.
علامت و یکای ممان اینرسی مقطع چیست ؟
ممان اینرسی، معمولا با حرف انگلیسی I نشان داده میشود. البته در صورت عمود بودن محور مبنا نسبت به مقطع، حرف انگلیسی J، علامت مورد استفاده برای نمایش این کمیت خواهد بود. یکای ممان اینرسی، طول به توان چهار (میلیمتر به توان چهار mm۴، اینچ به توان چهار in۴ و غیره) است.
مثال ۱: محاسبه ممان اینرسی تیر مستطیلی
بر اساس استاندارد IS، ابعاد مقطع تیرهای بتنی مورد استفاده در ساختمانهای مسکونی، برابر با ۲۲۵ میلیمتر در ۳۰۰ میلیمتر است. ممان اینرسی مقطع این تیرها را به دست بیاورید. محور x را موازی با طول مستطیل در نظر بگیرید.
تیرهای بتنی با مقطع بتنی طراحی و ساخته میشوند. بنابراین، به منظور تعیین ممان اینرسی مقطع این تیرها، از فرمولهای ممان اینرسی مستطیل استفاده میکنیم:
در هر یک از این فرمولها داریم:
- Ix: ممان اینرسی مستطیل نسبت به محور مرکزی x
- Iy: ممان اینرسی مستطیل نسبت به محور مرکزی y
- b: طول (قاعده) مستطیل برابر با ۳۰۰ میلیمتر
- h: عرض (ارتفاع) مستطیل برابر با ۲۲۵ میلیمتر
اکنون، مقادیر معلوم را درون رابطههای بالا قرار میدهیم. برای ممان اینرسی حول x داریم:
به این ترتیب، ممان اینرسی مقطع تیر حول محور مرکزی x برابر با ۲۸۴۷۶۵۶۲۵mm۴ است. ممان اینرسی مقطع تیر حول y را نیز به صورت زیر محاسبه میکنیم:
در نتیجه، ممان اینرسی مقطع تیر حول محور مرکزی y برابر با ۵۰۶۲۵۰۰۰۰mm۴ است. توجه داشته باشید که ممان اینرسی تیر، معمولا با یکای متر به توان چهار بیان میشود. بنابراین، در این مثال، ممان اینرسی مقطع تیر حول محورهای x و y به ترتیب برابر با و است.
اثبات ممان اینرسی مستطیل
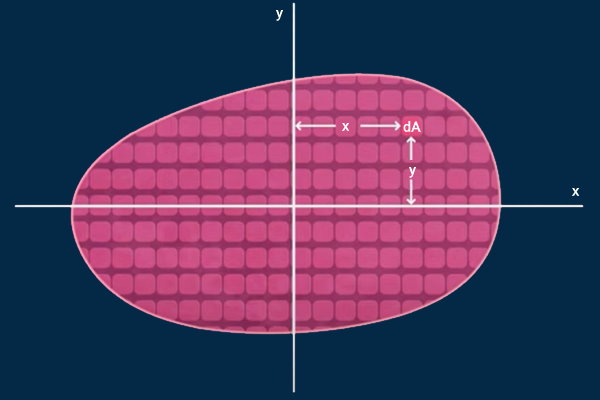
به منظور اثبات فرمول ممان اینرسی مستطیل، یک سطح مستطیلی مانند تصویر زیر را در نظر میگیریم. محورهای x و y از مرکز هندسی مستطیل عبور میکنند.
طول مستطیل برابر با b و عرض آن برابر با h است. محورهای x و y نیز از مرکز هندسی مستطیل عبور میکنند. به عبارت دیگر، محورهای x و y، مرکزی هستند. فرمول کلی ممان اینرسی سطح به صورت زیر نوشته میشود:
- Ix: گشتاور دوم سطح مستطیل نسبت به محور مرکزی x
- y: فاصله عمودی نقاط تا محور مرکزی x
- Iy: گشتاور دوم سطح مستطیل نسبت به محور مرکزی y
- x: فاصله عمودی نقاط تا محور مرکزی y
برای اثبات فرمول Ix، محور مرکزی x را به عنوان محور مبنای ممان اینرسی در نظر میگیریم. سپس، یکی از المانهای سطح مستطیل را انتخاب میکنیم.
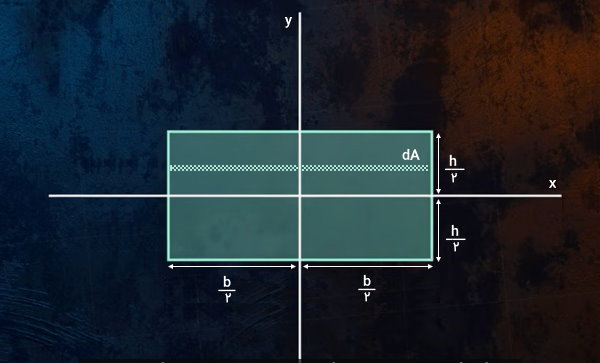
مساحت المانهای سطح را با dA نمایش میدهیم. این مساحت از حاصلضرب طول و عرض المان (dx و dy) در یکدیگر به دست میآید:
موقعیت قرارگیری المان dA در راستای محور x، در بازه تا و موقعیت قرارگیری آن در راستای محور y، در بازه تا تغییر میکند. با توجه به این اطلاعات، میتوانیم فرمول کلی ممان اینرسی سطح را به صورت زیر بازنویسی میکنیم:
اگر بخواهیم انتگرالگیری را نسبت dx انجام دهیم، عبارت y۲، به عنوان یک ثابت در نظر گرفته میشود. بنابراین میتوانیم آن را به پشت انتگرال اول منتقل کنیم:
حاصل انتگرال درون پرانتز برابر است با:
به این ترتیب، داریم:
در انتگرال بالا، b به عنوان یک ثابت در نظر گرفته میشود. بنابراین میتوانیم آن را به پشت انتگرال منتقل کنیم:
اکنون، جواب انتگرال دوم را به دست میآوریم:
این جواب را درون رابطه اصلی قرار میدهیم:
در نتیجه، فرمول ممان اینرسی مستطیل اثبات میشود. اگر به جای محور مرکزی x، محور مرکزی y را به عنوان مبنای ممان اینرسی قرار میدادیم، بازه انتگرال اول و دوم با یکدیگر جابجا و فرمول Iy اثبات میشد.
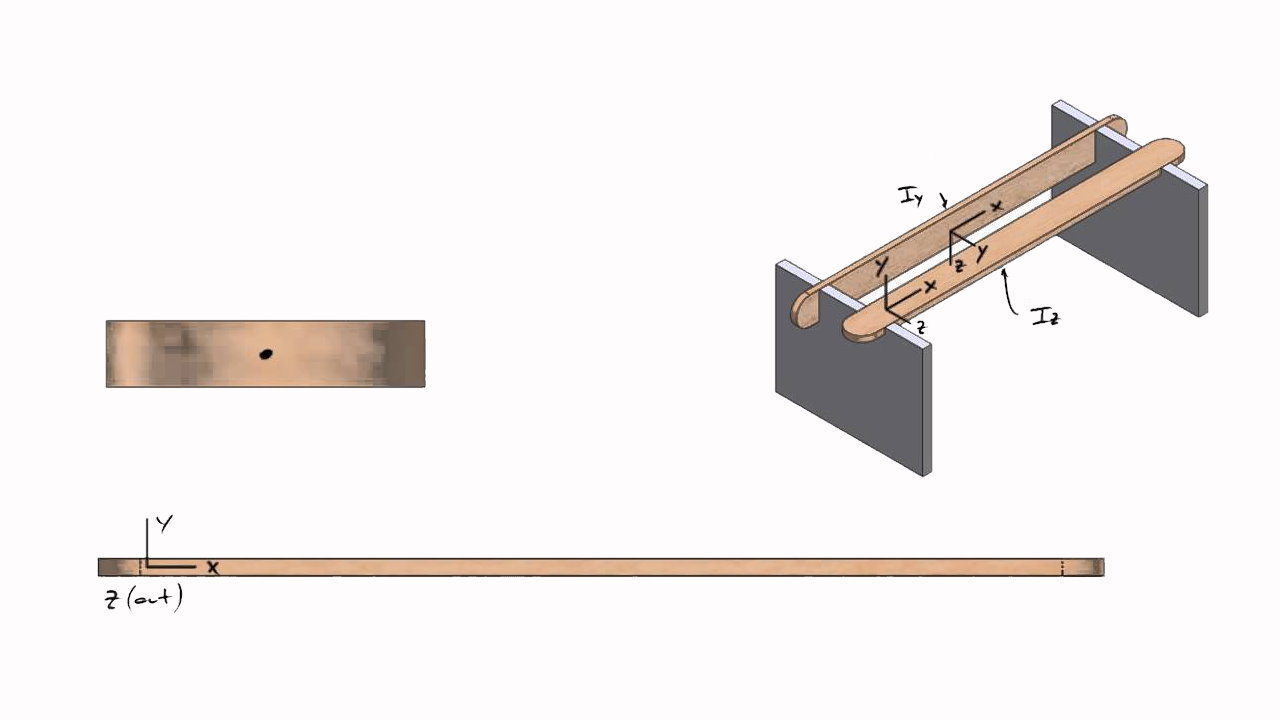
گشتاور قطبی مستطیل توپر
گشتاور قطبی یا «ممان اینرسی قطبی» (Polar Moment of Inertia)، کمیتی است که ارتباط بین شکل یک مقطع با مقاومت آن در برابر پیچش را نمایش میدهد. این کمیت نیز مانند ممان اینرسی سطح، با توجه به پراکندگی نقاط نسبت به محورهای مبنا تعریف میشود. در تعریف ممان اینرسی سطح مستطیل و فرمولهای آن، دیدیم که گشتاور دوم سطح با توجه به محورهای موجود بر روی صفحه مقطع (مانند محورهای مرکزی x و y) به دست میآید. در مورد گشتاور قطبی این موضوع متفاوت است. محاسبه این کمیت با توجه به محور عمود بر سطح مقطع (مانند محور مرکزی z) انجام میگیرد.
ممان اینرسی قطبی سطح مستطیل با حرف Jz ،J یا Iz نمایش داده میشود. یکای این کمیت نیز مانند گشتاور دوم سطح، برابر با طول به توان چهار است. ممان اینرسی قطبی مقاطع دوبعدی حول محور مرکزی z از رابطه زیر به دست میآید:
- J: ممان اینرسی قطبی
- Iz: گشتاور دوم سطح نسبت به محور مرکزی z
- r: فاصله هر جز تا محور z
- dA: مساحت دیفرانسیلی
بر اساس این رابطه، برای گشتاور قطبی مستطیل توپر داریم:
ممان اینرسی مستطیل توخالی
برخی از المانهای مورد استفاده در سازههای فولادی، با سطح مقطع مستطیل توخالی ساخته میشوند. تیرهای RHS یا اصطلاحا قوطی، یک المان مستطیلی شکل با مقطع توخالی است که کاربرد گستردهای در صنایع مختلف نظیر ساختمانسازی، پایپینگ، ساخت مبلمان و غیره دارد. مزیتهای مقاطع مستطیلی توخالی میتوان به نسبت مقاومت به وزن بیشتر، هزینه پایینتر و عملکرد مناسب در برابر بارهای پیچشی اشاره کرد. تصویر زیر، یک مستطیل توخالی (قوطی مستطیلی) با طول داخلی b۱، طول خارجی b۲، عرض داخلی h۱ و عرض خارجی h۲ را در دستگاه محورهای مختصات x-y نمایش میدهد.
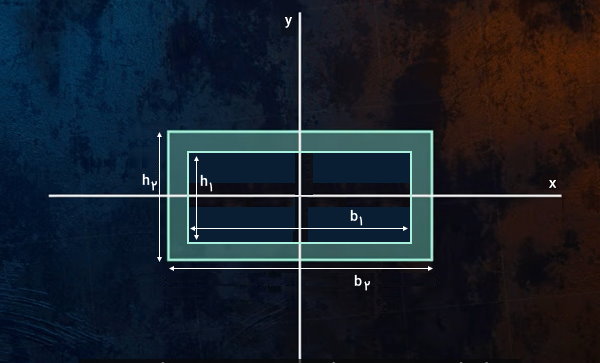
محورهای x و y از مرکز هندسی قوطی مستطیلی عبور میکنند. اگر هر یک از این محورها را به عنوان محور مبنا در نظر بگیریم، فرمول ممان اینرسی مقطع مستطیل توخالی به صورت زیر نوشته میشود:
$$ I _ x = \frac { b_ ۲ h _ ۲^ ۳ - b _ ۱ h _ ۱ ^ ۳ }{ ۱۲ } \ $$
- Ix: گشتاور دوم سطح مستطیل توخالی نسبت به محور مرکزی x
- Iy: گشتاور دوم سطح مستطیل توخالی نسبت به محور مرکزی y
- b۱: طول داخلی قوطی
- b۲: طول خارجی قوطی
- h۱: عرض داخلی قوطی
- h۱: عرض خارجی قوطی
ممان اینرسی قطبی مستطیل توخالی
گشتاور قطبی مستطیل توخالی، با استفاده از رابطه زیر به دست میآید:
به عبارت دیگر، گشتاور قطبی مستطیل توخالی حول محور مرکزی z برابر با مجموع گشتاورهای دوم سطح مستطیل توخالی حول محورهای مرکزی x و y است:
ممان اینرسی و گشتاور قطبی مستطیل جدار نازک
به مقاطع توخالی که ضخامت دیواره آنها بسیار کوچکتر از ابعادشان باشد، مقاطع جدار نازک میگویند. تصویر زیر، یک مقطع جدار نازک مستطیلی شکل را بر روی محورهای مرکزی x و y نمایش میدهد.
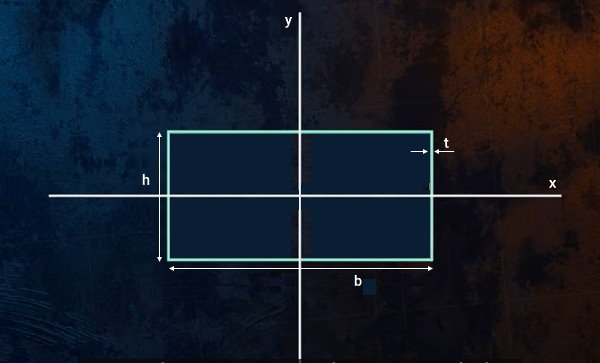
برای محاسبه ممان اینرسی مقاطع نازک، طول و عرض داخلی تعریف نمیشود. به جای این پارامترها، ضخامت جداره مقطع در محاسبات مورد استفاده قرار میگیرد. فرمول ممان اینرسی سطح مستطیل جدار نازک عبارت است از:
ممان اینرسی قطبی برای سطح مستطیل جدار نازک، حول محور مرکزی z، با استفاده از رابطه زیر به دست میآید:
پارامترهای موجود در این سه رابطه، عبارت هستند از:
- Ix: گشتاور دوم سطح مستطیل جدار نازک نسبت به محور مرکزی x
- Iy: گشتاور دوم سطح مستطیل جدار نازک نسبت به محور مرکزی y
- Iz: گشتاور قطبی مستطیل جدار نازک نسبت به محور مرکزی z
- b: طول مستطیل جدار نازک
- h: عرض مستطیل جدار نازک
- t: ضخامت جداره مستطیل
ممان اینرسی مستطیل دوران یافته
یک مستطیل توپر را در نظر بگیرید که حول مرکز هندسی خود، به اندازه زاویه θ دوران یافته است (تصویر زیر). مرکز هندسی مستطیل، بر روی مرکز محورهای مختصات x-y قرار دارد.
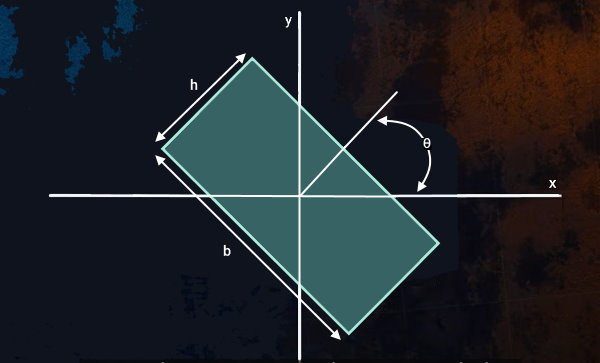
فرمول ممان اینرسی مستطیل دورانیافته بالا نسبت به محور مرکزی x عبارت است از:
فرمول گشتاور قطبی مستطیل دورانیافته نیز به صورت زیر نوشته میشود:
- Ix: گشتاور دوم سطح مستطیل توپر دورانیافته نسبت به محور مرکزی x
- Iz: گشتاور قطبی مستطیل توپر دورانیافته نسبت به محور مرکزی z
- θ: زاویه دوران مستطیل توپر نسبت به محور افقی
- b: طول مستطیل توپر
- h: عرض مستطیل توپر
مثال ۲: مقایسه ممان اینرسی مستطیل توپر و توخالی
یک قوطی فولادی به ضخامت ۰/۶ میلیمتر و ابعاد مقطع ۱۰ میلیمتر در ۲۰ میلیمتر را در نظر بگیرید. ممان اینرسی مقطع قوطی را به دست بیاورید. اگر این مقطع توپر بود، ممان اینرسی سطح آن چه تغییری میکرد؟ (راستای طول مستطیل، با راستای محور x موازی است.)
پارامترهای موجود در این سه رابطه، عبارت هستند از:
- Ix: گشتاور دوم سطح مستطیل جدار نازک نسبت به محور مرکزی x
- Iy: گشتاور دوم سطح مستطیل جدار نازک نسبت به محور مرکزی y
- b: طول مستطیل جدار نازک برابر با ۲۰ میلیمتر
- h: عرض مستطیل جدار نازک برابر با ۱۰ میلیمتر
- t: ضخامت جداره مستطیل برابر با ۰/۶ میلیمتر
به این ترتیب، برای ممان اینرسی قوطی حول x داریم:
ممان اینرسی قوطی حول محور y نیز برابر است با:
ممان اینرسی قوطی حول محورهای مرکزی x و y برابر با ۴۰۰ میلیمتر به توان چهار و ۸۰۰ میلیمتر به توان چهار است. اگر سطح مقطع قوطی، توپر بود، ممان اینرسی آن حول محورهای x و y به صورت زیر محاسبه میشد:
- Ix: ممان اینرسی مستطیل توپر نسبت به محور مرکزی x
- Iy: ممان اینرسی مستطیل توپر نسبت به محور مرکزی y
- b: طول (قاعده) مستطیل برابر با ۲۰ میلیمتر
- h: عرض (ارتفاع) مستطیل برابر با ۱۰ میلیمتر
در این شرایط، برای ممان اینرسی مستطیل توپر حول محور x داریم:
ممان اینرسی مستطیل توپر حول محور y برابر است با:
بنابراین، در صورت توپر بودن مقطع و ثابت بودن ابعاد، ممان اینرسی سطح حول محورهای x و y به ترتیب برابر با ۱۶۶۶/۶۷ میلیمتر به توان چهار و ۶۶۶۶/۶۷ میلیمتر به توان چهار میشود. همانطور که مشاهده میکنید، ممان اینرسی مقطع توپر حول محور x، بیش از ۴ برابر و حول محور y، بیش از ۸ برابر ممان اینرسی مقطع جدار نازک شد. در نتیجه، اختلاف قابلتوجهی بین ممان اینرسی سطوح توپر و توخالی وجود دارد. البته، قطعا مواد مورد استفاده در ساخت سطحهای توپر، به مراتب بیشتر از سطحهای توخالی است. طراحان، با تغییر ابعاد و شکل مقطعها، بین مواد مصرفی و ممان اینرسی مورد نیاز تعادل برقرار میکنند.
قضیه محورهای موازی در ممان اینرسی سطح مستطیل
فرمولهای ممان اینرسی مستطیل و دیگر شکلهای هندسی، معمولا بر اساس محورهای عبوری از مرکز هندسی نوشته میشوند. اگر محور مبنای مورد نظر بر روی محورهای عبوری از مرکز هندسی منطبق نباشد، فرمول محاسبه ممان اینرسی مقطع مستطیل تغییر میکند. به عنوان مثال، فرض کنید محور مبنای مورد نظر ما، خطی موازی با محور مرکزی xc و در فاصله d از این محور باشد.
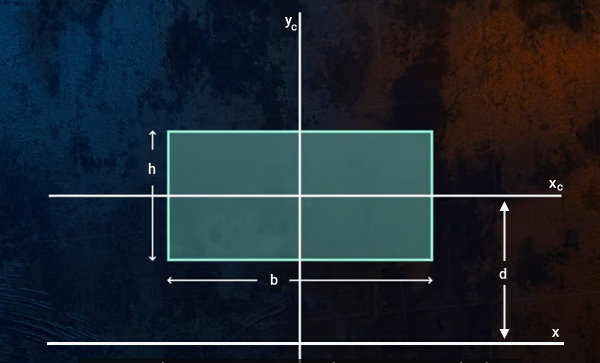
اگر بخواهیم ممان اینرسی مستطیل نسبت به محور دلخواه x را به دست بیاوریم، از فرمول زیر استفاده میکنیم:
- Ix: ممان اینرسی مستطیل نسبت به محور دلخواه و موازی با محور مرکزی xc
- Ixc: ممان اینرسی مستطیل نسبت به محور مرکزی xc
- A: مساحت سطح مقطع
- d: فاصله بین محور دلخواه x و محور مرکزی xc
- b: طول (قاعده) مستطیل
- h: عرض (ارتفاع) مستطیل
به فرمول بالا، «قضیه محورهای موازی» (Parallel Axis Theorem) میگویند. برای محورهای موازی با محور مرکزی yc داریم:
- Iy: ممان اینرسی مستطیل نسبت به محور دلخواه و موازی با محور مرکزی yc
- Iyc: ممان اینرسی مستطیل نسبت به محور مرکزی yc
- A: مساحت سطح مقطع
- d: فاصله بین محور دلخواه y و محور مرکزی yc
- b: طول (قاعده) مستطیل
- h: عرض (ارتفاع) مستطیل
مثال ۳: محاسبه ممان اینرسی مستطیل نسبت به محور دلخواه
یک تیر مستطیلی به مقطع ۲۵ در ۱۵ سانتیمتر را در نظر بگیرید. ممان اینرسی سطح مقطع تیر حول محور منطبق بر روی طول آن چقدر است؟
برای درک بهتر مسئله، شکل مقطع مستطیل مورد سوال را به همراه اجزای مختلف آن رسم میکنیم.
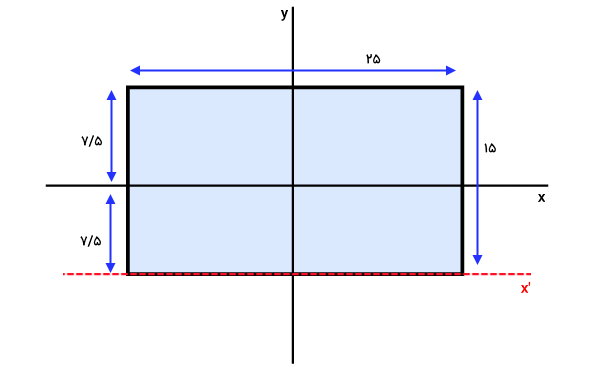
محور x و y را به عنوان محورهای گذرنده از مرکز هندسی مقطع در نظر میگیریم. محور 'x، محور منطبق بر روی طول مقطع و موازی با محور x است. بنابراین، فاصله این محور تا محور x، نصف عرض مستطیل (۷/۵ سانتیمتر) خواهد بود. به دلیل موازی بودن 'x با x، میتوانیم از قضیه محورهای موازی برای محاسبه ممان اینرسی سطح مقطع استفاده کنیم. بر اساس این قضیه داریم:
- 'Ix: ممان اینرسی مستطیل نسبت به محور دلخواه و موازی با محور مرکزی xc
- A: مساحت سطح مقطع برابر با حاصلضرب طول در عرض مستطیل (۱۵ × ۲۵)
- d: فاصله بین محور دلخواه 'x و محور مرکزی x برابر با ۷/۵ سانتیمتر
- b: طول (قاعده) مستطیل برابر با ۲۵ سانتیمتر
- h: عرض (ارتفاع) مستطیل برابر با ۱۵ سانتیمتر
مقادیر معلوم را درون رابطه بالا قرار میدهیم:
در نتیجه، ممان اینرسی مقطع تیر حول محور مورد نظر برابر با ۲۸۱۲۵ سانتیمتر به توان چهار است.
جدول ممان اینرسی مقاطع مستطیل شکل
در این بخش، فرمولهای ممان اینرسی سطوح مستطیلی شکل نظیر مربع، مستطیل توپر، مستطیل توخالی، مستطیل جدار نازک را در قالب جدول ارائه میکنیم.
جدول ممان اینرسی مربع
مربع، یکی از حالتهای خاص مستطیل است که در آن، طول و عرض با یکدیگر برابرند. فرمولهای ممان اینرسی سطح مربع، در جدول زیر آورده شدهاند.
| ممان اینرسی سطح مربع توپر | ||
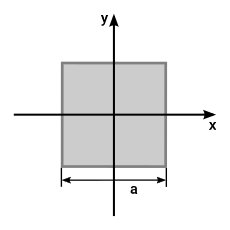 | ||
| ممان اینرسی سطح حول محور مرکزی x | a، اندازه ضلع مقطع مربعی است. | |
| ممان اینرسی سطح حول محور مرکزی y | ||
| ممان اینرسی سطح حول محور موازی با x و گذرنده از ضلع | ||
| ممان اینرسی سطح حول محور موازی با y و گذرنده از ضلع | ||
| گشتاور قطبی حول محور مرکزی z | ||
| گشتاور قطبی حول محور موازی با z | ||
جدول ممان اینرسی مستطیل توپر
جدول زیر، فرمولهای گشتاور دوم سطح مستطیل توپر را نمایش میدهد.
| ممان اینرسی سطح مستطیل توپر | ||
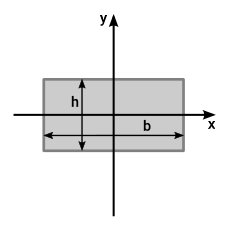 | ||
| ممان اینرسی سطح حول محور مرکزی x | b، طول مستطیل و h، عرض مستطیل است. | |
| ممان اینرسی سطح حول محور مرکزی y | ||
| ممان اینرسی سطح حول محور گذرنده از روی طول | ||
| ممان اینرسی سطح حول محور گذرنده از عرض | ||
| گشتاور قطبی حول محور مرکزی z | ||
| گشتاور قطبی حول محور موازی با z | ||
جدول ممان اینرسی مستطیل توخالی
فرمولهای گشتاور دوم سطح مستطیل توخالی، در جدول زیر نشان داده شدهاند.
| ممان اینرسی سطح مستطیل توخالی | ||
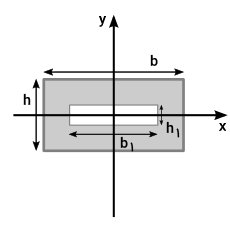 | ||
| ممان اینرسی سطح حول محور مرکزی x | b۱ و b۲، طولهای داخلی و خارجی و h۱ و h۲، عرضهای داخلی و خارجی مستطیل هستند. | |
| ممان اینرسی سطح حول محور مرکزی y | ||
| ممان اینرسی سطح حول محور گذرنده از روی طول | ||
| ممان اینرسی سطح حول محور گذرنده از عرض | ||
| گشتاور قطبی حول محور مرکزی z | ||
| گشتاور قطبی حول محور موازی با z | ||
جدول ممان اینرسی مستطیل جدار نازک (قوطی)
جدول زیر، فرمولهای گشتاور دوم سطح مستطیل جدار نازک را نمایش میدهد.
| ممان اینرسی سطح مستطیل توخالی | ||
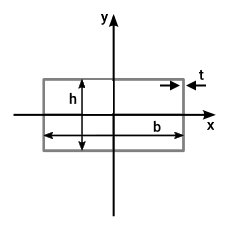 | ||
| ممان اینرسی سطح حول محور مرکزی x | b، طول مستطیل، h، عرض مستطیل و t، ضخامت دیواره مستطیل است. | |
| ممان اینرسی سطح حول محور مرکزی y | ||
| ممان اینرسی سطح حول محور گذرنده از روی طول | ||
| ممان اینرسی سطح حول محور گذرنده از عرض | ||
| گشتاور قطبی حول محور مرکزی z | ||
| گشتاور قطبی حول محور موازی با z | ||
تفاوت گشتاور دوم سطح با ممان اینرسی چیست ؟
«لختی دورانی» (Rotational Inertia) یا «ممان اینرسی» (Moment of Inertia)، کمیتی است که میزان مقاومت یک جسم در برابر شتاب زاویهای را نمایش میدهد. به زبان سادهتر، به گشتاور مورد نیاز برای دوران یک جسم با شتاب زاویهای مورد نظر، ممان اینرسی میگویند. این کمیت، از جمع حاصلضربهای جرم هر ذره از جسم در فاصله آن ذره تا محور دوران به دست میآید. ممان اینرسی با عنوان «جرم زاویهای» (Angular Mass) نیز شناخته میشود. واحد این کمیت در سیستم یکاهای بینالمللی (SI)، کیلوگرم در متر مربع (Km۲) است. تصویر زیر ممان اینرسی چند جسم سهبعدی با جرمهای یکسان و شکلهای متفاوت را نمایش میدهد.

هر چه ممان اینرسی یک جسم بیشتر باشد، شتاب زاویهای آن در حین دوران کمتر خواهد بود. به عنوان مثال، در تصویر بالا، کره توپر، زودتر از بقیه اجسام از خط پایان عبور میکند؛ چراکه ممان اینرسی آن به ترتیب از استوانه توپر، کره توخالی و استوانه توخالی کمتر است.
سوالات متداول در رابطه با ممان اینرسی مستطیل
در این بخش، به برخی از سوالات پرتکرار در رابطه با ممان اینرسی مستطیل به طور خلاصه پاسخ میدهیم.
گشتاور دوم سطح معرف چیست ؟
ممان اینرسی سطح، معیاری برای ارزیابی تاثیر شکل مقطع بر مقاومت خمشی ناشی از بارگذاری است.
تعریف ممان اینرسی مستطیل چیست ؟
ممان اینرسی مستطیل، کمیتی برای نمایش میزان پراکندگی نقاط سطح مقطعهای مستطیلی نسبت به یک محور مشخص است.
یکای ممان اینرسی سطح چیست ؟
یکای ممان اینرسی سطح، طول به توان چهار (میلیمتر به توان چهار، سانتیمتر به توان چهار، متر به توان چهار، اینچ به توان چهار و غیره) است.
فرمول ممان اینرسی مقطع مستطیل چیست ؟
فرمول ممان اینرسی سطح مستطیل حول محور x، برابر با Ix=bh^۳/۱۲ و حول محور y، برابر با Iy=hb^۳/۱۲ است.
قضیه محورهای موازی در محاسبه ممان اینرسی مقطع مستطیل چیست ؟
قضیه محورهای موازی در مقطعههای مستطیلی، رابطه بین ممان اینرسی حول محورهای مرکزی و محورهای موازی با آنها را نمایش میدهد. بر اساس این قضیه، با داشتن فاصله بین محور مرکزی و محور موازی با آن، میتوان ممان اینرسی حول محور مرکزی را به دست آورد.













سلام
«ممان اینرسی آن به ترتیب از استوانه توپر، کره توخالی و استوانه توخالی بیشتر است.» اشتباه است
با توجه به جرم یکسان، کمتر صحیح است:
ممان اینرسی آن به ترتیب از استوانه توپر، کره توخالی و استوانه توخالی کمتر است.
با سلام و وقت بخیر؛
متن مقاله اصلاح شد. ممنون از توجه شما.
از همراهیتان با مجله فرادرس سپاسگزاریم
((هر چه مقدار ممان اینرسی مقطع بیشتر باشد، مقاومت آن در برابر خمش کمتر خواهد بود))، متن فوق اشتباه تایپی دارد هر چه ممان اینرسی افزایش یابد مقاومت آن در برابر خمش بیشتر می شود نه کمتر .
با سلام،
متن بازبینی و اصلاح شد،
با تشکر از همراهی شما با مجله فرادرس