انواع نمودار در ریاضیات — به زبان ساده

بدیهی است که همه نمودارها شبیه هم نیستند، اما چه تفاوتی بین انواع مختلف نمودارها وجود دارد؟ در این نوشته تلاش می‌کنیم به این سؤال پاسخ دهیم و انواع نمودارهایی که وجود دارند را به همراه توضیحی کوتاه معرفی کنیم.

انواع نمودار

در ابتدا سعی می‌کنیم با انواع مختلف نمودار به طور مختصر آشنا شویم. همان طور که می‌توان هر آنچه در جهان است را به دو دسته «موزها» و «غیر موزها» تقسیم کرد، نمودارها را نیز می‌توان به دو دسته «نقشه» و «غیر نقشه» تقسیم نمود.

نمودارهای نقشه نمودارهای هستند که در آن‌ها x و y متناظر با مسافت هستند. این مسافت می‌تواند بر مبنای فوت، متر یا هر چیز دیگری بیان شده باشد. به هر حال مختصات طول و عرض نشان دهنده نوعی موقعیت مکانی هستند.

فیلم آموزش نرم افزار گرافر – رسم نمودارهای حرفه ای با Grapher در فرادرس

کلیک کنید

نمودارهای غیر نقشه یا همه انواع نمودارهای دیگر، نمودارهایی هستند که در آن‌ها مختصات به معنی مسافت نیستند، بلکه می‌توانند نشان دهنده میزان تولید، زمان یا هر متغیر دیگری باشند. برخی از نمودارهای غیر نقشه، نمودارهای ترکیبی هستند که در آن‌ها یک محور نماینده مسافت و نماینده دیگر نشان دهنده متغیری به جز مسافت است.

تا اینجا متوجه شدیم که نمودارها همگی از یک نوع نیستند. در ادامه آن‌ها را بیشتر توضیح می‌دهیم.

نمونه‌هایی از نمودار

نمودار نقشه زیر را به عنوان یک مثال نوعی در نظر بگیرید:

فرض کنید می‌خواهیم از نقطه فرضی (A (1, 1 به نقطه (B (4,5 برویم. همچنین تصور کنید این سفر نوعی هزینه به همراه دارد، مثلاً هزینه زمانی، سوخت مورد استفاده یا هر هزینه دیگری که تصور کنید. هدف ما این است که این هزینه را با هر چه کوتاه‌تر کردن مسیر به کمترین مقدار ممکن برسانیم.

می‌دانیم که کوتاه‌ترین مسافت بین دونقطه، خط مستقیمی است که آن دو را به هم وصل می‌کند. با استفاده از قضیه فیثاغورث درمی‌یابیم که این مسافت 5 واحد است (مثلث قائم‌الزاویه‌ای با اضلاع 3، 4 و 5 ایجاد می‌شود.)

اگر تصمیم بگیریم که در راستای اضلاع این مثلث حرکت کنیم، و در یک خط مستقیم ابتدا به (4،1) و سپس از آنجا به نقطه B برویم باید 7 واحد را طی کنیم. بدیهی است که رفتن مستقیم از A به B مسیری کم‌هزینه‌تر است.

مثالی از نمودار غیر نقشه

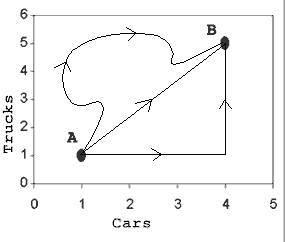
اینک یک نمودار معمولی غیر نقشه را تصور کنید که تعداد خودروها و کامیون‌ها را در یک شرکت کرایه خودرو نشان می‌دهد.

فرض کنید این شرکت می‌خواهد موجودی خود را افزایش دهد. در حال حاضر در نقطه A یا یک خودرو و یک کامیون قرار دارد. شرکت می‌خواهد به نقطه B (چهار خودرو و 5 کامیون) برود. اگر هزینه این «سفر» صرفاً خرید خودروها و کامیون‌های جدید باشد، این شرکت چه مقدار باید هزینه کند؟

این مسئله دشواری نیست. می‌توانیم ببینیم که مهم نیست شرکت چه مسیری را انتخاب کند، چون در هر صورت هزینه همان خواهد بود. آن‌ها باید 3 خودرو و 4 کامیون بخرند. آن‌ها می‌توانند اول همه خودروها و سپس کامیون‌ها را بخرند یا برعکس و یا هر ترکیبی از این خریدها. آن‌ها حتی می‌توانند خودروها و کامیون‌های بیشتر از این مقدار بخرند و بعد تعدادی مازاد آن‌ها را بفروشند که در این صورت یک مسیر پر پیچ و خم خواهیم داشت. اگر شرکت اول یک نوع و بعد یک نوع دیگر را بخرد در این صوت یک مثلث خواهیم داشت.

اینک سؤال این است که چرا این دو مثال متفاوت هستند؟ دلیل ساده این است که مسافت در نمودارهای غیر نقشه اهمیتی ندارد. به بیان ساده‌تر اگر یک نقشه محورهایی از نوع فاصله نداشته باشد، در این صورت «مسافت» در آن نمودار هیچ اهمیتی ندارد. در این مورد قضیه فیثاغورث هیچ کمکی به ما نمی‌کند. دانستن این که کوتاه‌ترین فاصله بین دو نقطه، یک خط مستقیم است نیز هیچ کمکی نمی‌کند. در هر صورت ما باید در نهایت 4 خودرو و 5 کامیون داشته باشیم و مهم نیست که چگونه آن‌ها را می‌خریم. اما این پایان داستان نیست.

کوتاه‌ترین مسیر یا ارزان‌ترین مسیر

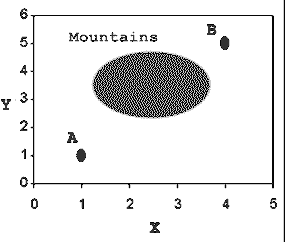
تا این جا متوجه شدیم که در نمودارهای نقشه، انتخاب یک مسیر مستقیم، بهترین گزینه است. اما در نمودارهای غیر نقشه در این خصوص مزیتی وجود ندارد. اینک به نمودار نقشه زیر توجه کنید که در آن عوارض جغرافیایی مانند کوه نمایش یافته است.

ما در این نقشه نیز می‌خواهیم از نقطه A به نقطه B برویم؛ اما در این مورد، بدین منظور باید از کوهستان عبور کنیم. فرض کنید که در کوهستان هزینه حرکت 10 برابر حد معمول است. اینک می‌بینیم که کوتاه‌ترین مسیر دیگر معنی قبلی خود را ندارد. انتخاب مسیری که از اضلاع غیر وتر مثلث عبور می کند، در این مورد ارزان‌تر خواهد بود. یعنی ابتدا از A به نقطه (4،1) برویم و سپس از آنجا به B برویم.

فیلم آموزش نرم افزار Circos برای رسم نمودارهای حرفه ای در فرادرس

کلیک کنید

در نمودارهای مسافت که هزینه سفر در نقاط مختلف متفاوت است، ممکن است ارزان‌ترین مسیر طولانی‌تر از مسیری باشد که خط مستقیم ارائه می‌کند. در این حالت علاوه بر جنبه‌های ریاضی و فیزیکی که در آن مسافت را اندازه‌گیری می‌کنیم، عامل دیگری (به صورت هزینه سفر) نیز دخیل است که در نقاط مختلف متفاوت است.

مثال پیشرفته‌تر: امواج نوری

یک مثال خوب برای نمودار ترکیبی (یک محور مسافت باشد و محور دیگر چنین نباشد)، نمودار معمولی است که برای امواج نوری ترسیم می‌شود. در ادامه نمونه‌ای از چنین موج‌هایی ارائه شده است:

نمودار فوق یک تصویر عالی است؛ اما ممکن است بیننده را سردرگم کند. امواج نوری مانند یک قطار هوایی بالا و پایین نمی‌روند. اما وقتی یک بیننده غیر متخصص به این نمودار نگاه می‌کند، به راحتی چنین تصوری در ذهن وی ایجاد می‌شود.

دامنه موج

در واقع نمودار فوق می‌خواهد بیان کند که وقتی نور مسافتی را طی می‌کند، میزان جابجایی (شدت) آن تغییر می‌یابد. دامنه موج (amplitude) بیشینه مقدار این جابجایی را نشان می‌دهد. خود نور می‌تواند مسیر مستقیمی را طی کند. برای نشان دادن این مسئله میزان تغییرات (جابجایی) نور را به نمودار فوق اضافه کردیم:

دقت کنید که میزان روشنایی نوار زیرین چه رابطه‌ای با جابجایی موج دارد. وقتی موج در قله قرار دارد، میزان روشنایی نیز بیشینه است که نشان دهنده بالاترین شدت در جهت مثبت است. وقتی موج وارد قعر خود می‌شود نوار نیز به رنگ تیره درمی‌آید که نشان می‌دهد تاریکی مطلق است و میزان روشنایی در جهت منفی در بالاترین مقدار خود است. در میانه، جایی که روی محور صفر قرار می‌گیرد، مقدار جابجایی خنثی است و از این رو شدتی ندارد. البته توجه داشته باشید که انتخاب عبارت‌های مثبت و منفی دلخواه هستند.

فیلم آموزش رسم نمودارهای پیشرفته در اکسل در فرادرس

کلیک کنید

این معنی دقیقی است که نمودار فوق می‌خواهد انتقال دهد؛ اما به هر حال برای ذهن ما دشوار است که به نمودار فوق نگاه کند و تصور نکند که نور مسیری نوسانی را مانند قطار هوایی به صورت بالا و پایین طی می‌کند.

بدیهی است که امواج می‌توانند مانند هر چیز دیگری در جهان مسیری نوسانی داشته باشند؛ اما منظور نمودار فوق اشاره به این مسئله نیست. نکته اصلی این است که شدت موج نوسان دارد، هر چند خط سیر آن کاملاً مستقیم باشد.

اگر از دانشمندان این رشته بپرسید، خواهند گفت که نور ماهیتی دوگانه ذره-موج دارد که در آن شدت یک ذره با فاصله‌ای که از مبدأ دارد تغییر می‌یابد؛ اما اگر می‌خواهید معنی ساده نمودار فوق را درک کنید، همان است که در بخش فوق بیان کردیم.

جمع‌بندی

مسافت در نمودارهای نقشه‌ای اهمیت دارد با این که خط مستقیم می‌تواند کوتاه‌ترین مسیر باشد؛ اما لزوماً ارزان‌ترین مسیر نیست. در نمودارهای غیر نقشه، مسافت روی نمودار به معنی موقعیت فیزیکی نیست. محورها مسافت را نشان نمی‌دهند و از این رو مسیرهای روی نمودار با موقعیت‌هایی که یک نفر طی می‌کند متناظر نیستند. نباید تصور کنید که وقتی اشیا روی یک نمودار غیر نقشه مسیری منحنی را طی کرده‌اند، در دنیای واقعی نیز درگیر مسیر خمیده هستند.

اگر این نوشته مورد توجه شما قرار گرفته است، پیشنهاد می‌کنیم موارد زیر را نیز بررسی کنید:

• مجموعه آموزش‌های ریاضیات
• مجموعه آموزش‌های دروس رسمی دبیرستان و پیش‌دانشگاهی
• نمودارهای پراکندگی – به زبان ساده
• نمودار های میله ای و ستونی – به زبان ساده
• آموزش نمایش داده ها و ترسیم نمودار در اکسل
• نمودار دایره ای – به زبان ساده

==