تحلیل سری زمانی با پایتون – مدل های ترکیبی و پیچیده

تحلیل سری زمانی و انتخاب مدل مناسب برای تحلیل آن‌ها یکی از مهم‌ترین بخش‌های تجزیه و تحلیل داده‌های مرتبط با زمان است. انجام محاسبات و رسم نمودارها، از وظایف اصلی «تحلیل‌گر داده» (Data Scientist) محسوب می‌شود. زبان برنامه نویسی پایتون (Python) از ابزارهای مفید در این امر محسوب می‌شود. در سری مطالب دنباله‌ای تحلیل سری زمانی با پایتون، در قسمت اول، به بررسی مفاهیم اولیه در مبحث سری زمانی پرداختیم. در بخش دوم، مدل‌هایی پایه برای سری زمانی و نحوه ایستا کردن (Stationary) آن‌ها را مرورد خواهیم کرد. در این بخش یعنی قسمت سوم، به معرفی مدل‌های ترکیبی و پیچیده سری زمانی خواهیم پرداخت و پیاده‌سازی چنین مدل‌هایی را با زبان برنامه‌نویسی پایتون مرور خواهیم کرد.

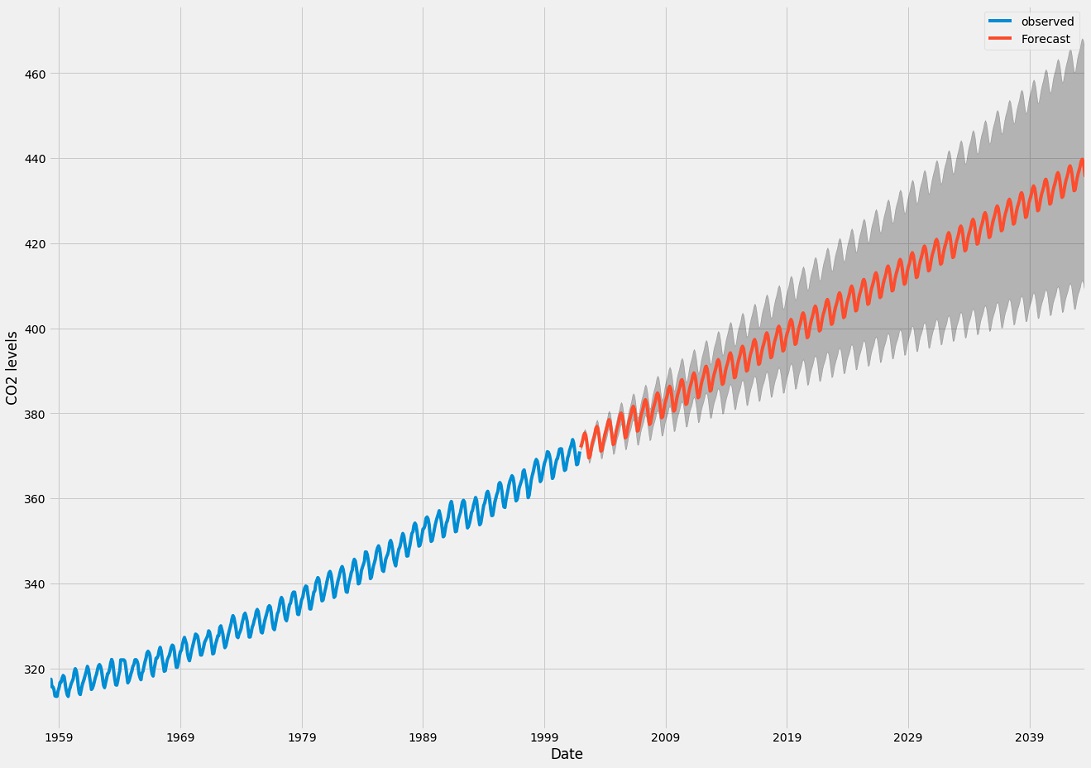
برای آشنایی بیشتر با مقدمات مربوط به مبحث سری زمانی بهتر است نوشتار تحلیل سری زمانی — تعریف و مفاهیم اولیه را بخوانید. همچنین خواندن مطلب سری زمانی در علم داده — از صفر تا صد نیز خالی از لطف نیست.

تحلیل سری زمانی با پایتون به صورت دنباله‌ای از نوشتارها در سه بخش ارائه می‌شود.

• بخش نخست: تحلیل سری زمانی با پایتون تحلیل سری زمانی با پایتون --- مقدمات و مفاهیم اولیه
• بخش دوم: تحلیل سری زمانی با پایتون --- معرفی انواع مدل‌ها
• بخش سوم: تحلیل سری زمانی با پایتون --- مدل‌های ترکیبی و پیچیده

تحلیل سری زمانی و مدل‌های ترکیبی و پیچیده

بسیاری از پدیده‌های مرتبط با سری زمانی، به صورت ترکیبی از مدل‌های ساده تشکیل می‌شوند. در این بخش به معرفی مدل‌های ترکیبی پرداخته و توسط توابع موجود در کتابخانه pandas در زبان برنامه نویسی پایتون، شبیه‌سازی و مدل‌سازی را انجام خواهیم داد. در ادامه به بررسی مدل ARMA ،ARIMA ،ARCH و GARCH خواهیم پرداخت.

مدل اتورگرسیو میانگین متحرک (Autoregressive Moving Average)

همانطور که حدس می‌زنید، این مدل به صورت ترکیبی از دو مدل ساده‌ $$AR(p)$$ و $$MA(q)$$ ساخته می‌شود. به همین دلیل نیز برای نمایش این مدل از نماد $$ARMA(p,q)$$ استفاده می‌شود. حال از این مدل به منظور تفسیر سری زمانی داده‌های مالی استفاده می‌کنیم.

• مدل‌های $$AR (p)$$ سعی دارند گشتاور و اثر برگشت‌ به میانگین که اغلب در بازارهای تجاری مشاهده می شود را توصیف کنند.
• مدل‌های $$MA(q)$$ نیز به منظور بررسی شوک‌ها، نویزها را مدل‌سازی کنند. به این ترتیب رویدادهای غیرمنتظره (مثل درآمدهای میلیاردی یا حمله تروریستی) در مدل منظور می‌شوند.

ضعف مدل $$ARMA$$ در این است که قادر به شناسایی و مدل‌سازی اثرات نوسانات خوشه‌ای برای داده‌های سری زمانی مرتبط با داده‌های مالی نیست. مدل اتورگرسیو میانگین متحرک به بیان ریاضی به صورت زیر نوشته می‌شود.

$$\large x_t=a_1x_{t-1}+a_2x_{t-2}+\cdots+w_t+b_1w_{t-1}+\cdots+b_qw_{t-q}$$

این رابطه را به شکل ساده‌تری نیز می‌توان نشان داد. کافی است از نماد جمع در رابطه استفاده کنیم.

$$\large x_t=\sum_{i=1}^p a_ix_{t-i}+w_t+\sum_{i=1}^qb_iw_{t-i}$$

حال زمان مناسبی است که با استفاده از تابع ARMA در پایتون داده‌هایی با این مدل را با پارامترهای p=2 و q=2 شبیه‌سازی کنیم. آنگاه آن‌ها را با چنین مدلی برازش کرده و نمودارهای مرتبط با سری زمانی را ترسیم می‌کنیم. در ادامه کد مربوطه قابل مشاهده است. توجه داشته باشید که در اینجا مقدار $$a_1=0.5, a_2=-0.25, b_1=0.5, b_2=-0.3$$ است.

با اجرای این کد، نمودارها ترسیم شده و نتیجه مدل‌سازی توسط تابع summary محاسبه می‌شود.

جدول محاسباتی برای مدل نیز مطابق با تصویر زیر خواهد بود.

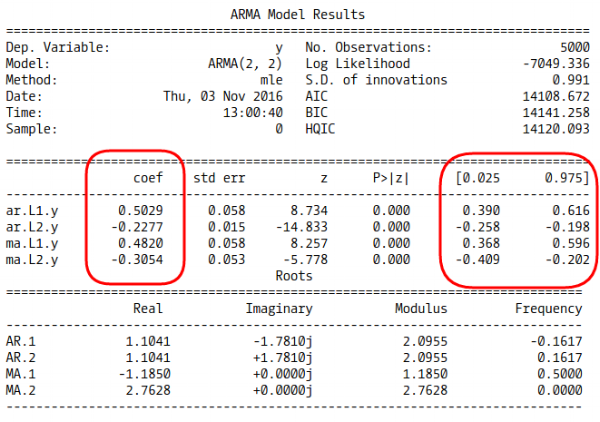
همانطور که دیده می‌شود، مدل به درستی پارامترها را پیش‌بینی کرده است. فاصله اطمینان ۹۵٪ نیز شامل پارامترها شده است. همین روند را برای مدل $$ARMA(3,2)$$ اجرا خواهیم کرد. یعنی داده‌هایی با توجه به این مدل شبیه‌سازی کرده و سپس سعی می‌کنیم با در نظر گرفتن مقدارهای مختلف $$p$$ و $$q$$، به بهترین برآورد مدل دست پیدا کنیم. انتخاب مدل را توسط معیار سنجش تناسب مدل به نام AIC که به «معیار اطلاع آیکاکی» (Akaike information criterion) معروف است انجام می‌دهیم. هر مدلی که مقدار AIC کمتری داشته باشد، مناسب‌تر است، زیرا اطلاعات کمتری توسط مدل از دست خواهد رفت. دستورات زیر به منظور اجرای چنین محاسباتی نوشته شده است. توجه داشته باشید که در اینجا مقدار $$a_1=0.5, a_2=-0.25, a_3=0.4, b_1=0.5, b_2=-0.3$$ است.

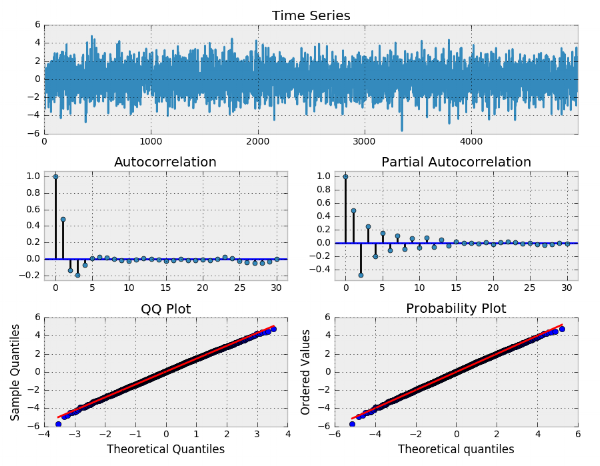
نمودارهای تحلیل سری زمانی یکی از قسمت‌های خروجی این برنامه است. به نمودارها توجه کنید.

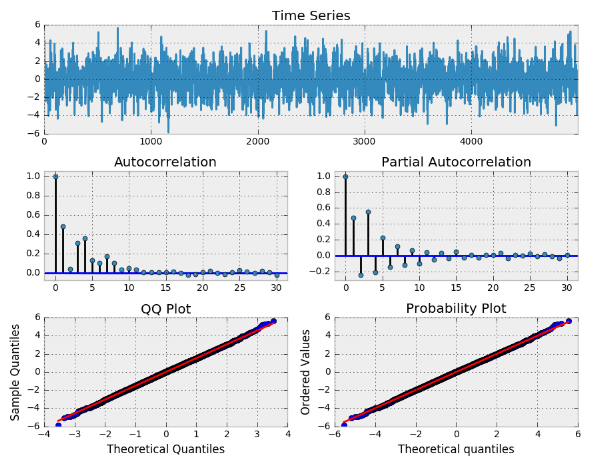
نرمال بودن باقی‌مانده کاملا مشخص است. همچنین سیر نزولی همبستگی در نمودار ACF و PACF به وضوح دیده می‌شود. خروجی مربوط به مدل نیز در تصویر زیر قابل مشاهده است.

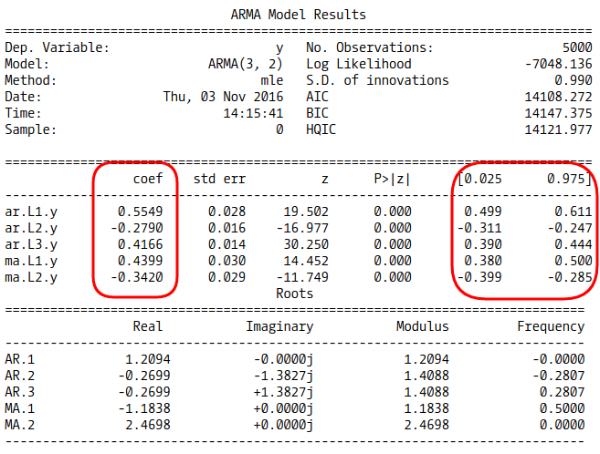
همانطور که در برنامه مشخص است، بهترین مدل که دارای کمترین میزان AIC باشد در یک حلقه تکرار، بدست آمده و خروجی را تشکیل می‌دهد. ضرایب بدست آمده نزدیک مقدارهای واقعی هستند. از طرفی فاصله اطمینان ۹۵٪ نیز شامل پارامتر واقعی است.

مقدار AIC برای مدل نهایی به صورت زیر است.

$$\large aic:\; 14108.27213\; |\; order:\; (3, 2)$$

در ادامه به بررسی باقی‌مانده‌های مدل توسط تابع tsplot می‌پردازیم. همانطور که نمودارها نشان می‌دهند، باقی‌مانده‌ها، نرمال و ناهمبسته هستند. بنابراین به نظر می‌رسد که مدل برای چنین داده‌های بسیار مناسب است.

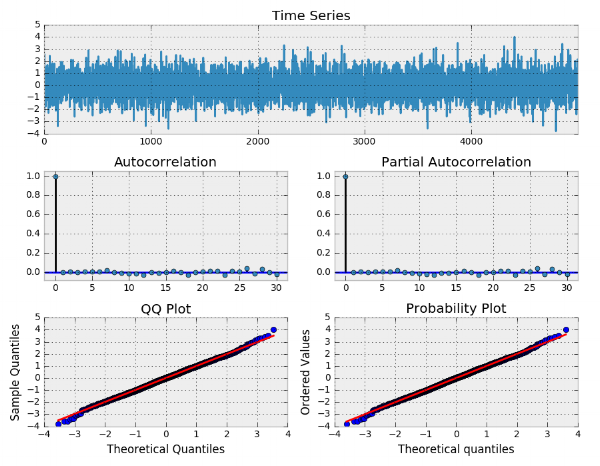
در ادامه برای داده‌های واقعی SPY مدل $$ARMA$$ را برازش می‌دهیم. انتخاب مرتبه‌های $$p$$ و $$q$$ نیز توسط معیار AIC صورت می‌گیرد. نمودار tsplot برای این داده‌ها در تصویر زیر قابل مشاهده است.

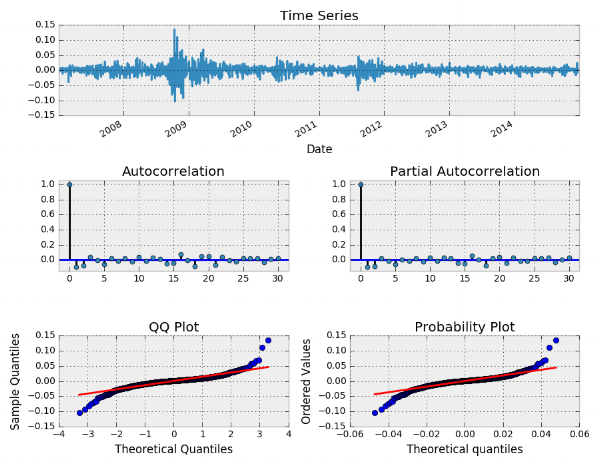
حال به کمک دستورات زیر به تحلیل و برازش مدل مناسب برای این داده‌ها خواهیم پرداخت.

نتیجه برای مرتبه‌های مدل به صورت زیر است. مقدار AIC نیز مشاهده می‌شود.

$$\large aic:\; -11518.22902\; |\; order:\; (4, 4)$$

در ادامه به بررسی باقی‌مانده‌های حاصل از برازش مدل می‌پردازیم. نمودارهای مربوطه، نشانگر مطلوب بودن مدل هستند. همانطور که مشخص است ACF و PACF به صفر رسیده‌اند و نمودارهای Q-Q plot و P-P plot‌، نرمال بودن باقی‌مانده ها را البته با دم‌های سنگین تایید می‌کنند. با توجه به نمودار اول در قسمت‌های متمایز شده، مشخص است که شوک‌های شدیدی در سری زمانی وجود دارد که فرض ثابت بودن واریانس فرایند ایستا را زیر سوال می‌برد. این حالت را به نام «ناهمسانی شرطی» (conditional heteroskedasticity) می‌شناسیم.

مدل اتورگرسیو یکپارچه میانگین متحرک (Autoergressive Integrated Moving Average)

یک حالت از توسعه مدل $$ARMA$$ به عنوان مدل «اتورگرسیو یکپارچه میانگین متحرک» $$ARIMA$$ معروف است. همانطور که در قبل گفته شد، اگر سری زمانی، ایستا نباشد می‌توان به کمک تبدیل تفاضلی آن را به حالت ایستا درآورد. در قسمت اول از این نوشتارها به مثالی برخورد کردیم که تفاضل‌گیری مرتبه اول برای قدم‌های تصادفی نرمال باعث ایستا شدن سری زمانی می‌شد.

فیلم آموزش تبدیل لگاریتمی و تفاضل گیری در پیش پردازش سری های زمانی (رایگان) در فرادرس

کلیک کنید

در مدل $$ARIMA$$ نیز از همین خاصیت استفاده کرده و برای سری‌های زمانی ناایستا، به کمک عملگر تفاضل‌گیری، ایستایی را ایجاد و مدل مناسب را ارائه خواهیم داد. این مدل دارای سه پارامتر $$p,d,q$$ است. پارامتر $$p$$ که درست به مانند مدل $$AR$$ عمل می‌کند. همچنین پارامتر $$q$$ نیز مطابق با مدل $$MA$$ خواهد بود. به این ترتیب پارامتر $$d$$ مرتبه تفاضل‌گیری سری زمانی را تعیین و مشخص می‌کند.

همانطور که در قبل مشاهده کردید، تابع np.diff عمل تفاضل‌گیری را انجام می‌دهد. در کتابخانه pandas توابع ()DataFrame.diff()/Series.diff فقط به منظور تفاضل‌گیری مرتبه ۱ به کار می‌روند. در حالیکه در مدل $$ARIMA$$ ممکن است به تفاضل‌گیری مراتب بالاتر احتیاج داشته باشیم. در ادامه به بررسی تعیین پارامترهای $$p,d,q$$ در مدل $$ARIMA$$ برای داده‌های SPY پرداخته‌ایم. ملاک انتخاب بهترین مدل نیز در اینجا کوچکترین AIC در نظر گرفته شده است.

با توجه به اجرای این کد، پارامترهای مدل به صورت زیر برآورد می‌شوند.

$$\large aic:\; -11518.22902\; |\; order:\; (4, 0, 4)$$

به این ترتیب مشخص است که مدل مناسب به صورت $$ARIMA(4,0,4)$$ خواهد بود. با توجه به این پارامترها، $$d=0$$ است و به نظر می‌رسد که تفاضل‌گیری نیاز نیست. البته لازم به یادآوری است که در مرحله قبلی برای محاسبه نرخ بازگشت سهام (Stock Returns) از تفاضل‌گیری مرتبه اول برای لگاریتم ارزش‌های سهام استفاده کردیم.

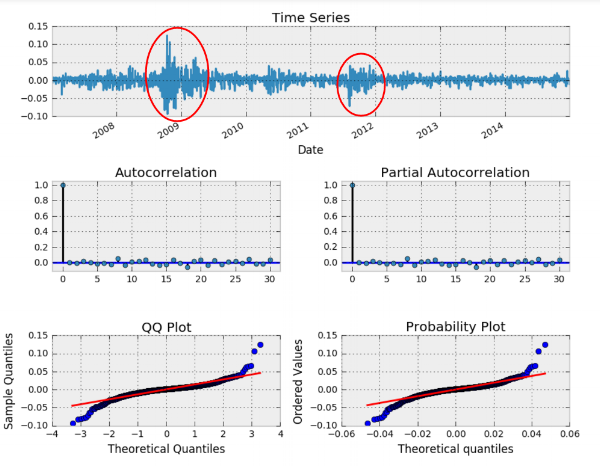
حال به بررسی نمودار tsplot برای ارزیابی باقی‌مانده‌های مدل می‌پردازیم. همانطور که می‌بینید، در سال ۲۰۰۹ و ۲۰۱۲ پراکندگی به صورت خارج از کنترل تغییر می‌کند.

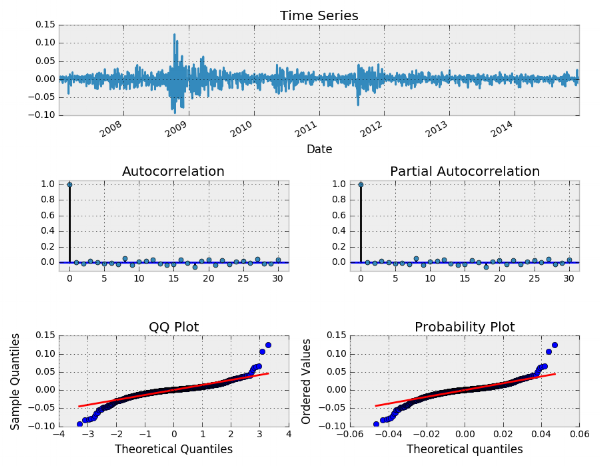
با توجه به توضیحات قبلی و مناسب بودن مدل تولید شده، حال به کمک این مدل، می‌توانیم پیش‌بینی ساده‌ای از آینده این سری زمانی داشته باشیم. به این ترتیب با استفاده از تابع ()forecast مطابق با کد زیر این کار را صورت می‌دهیم. این پیش‌بینی برای ۲۱ روز آینده سری زمانی SPY با فاصله اطمینان‌های ۹۵٪ و ۹۹٪ صورت گرفته است.

از آنجایی که از تابع fc_all.head استفاده شده، نتیجه برای چند روز اول پیش‌بینی و مطابق با جدول زیر نمایش داده می‌شود.

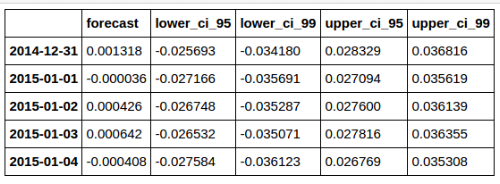
به کمک برنامه زیر نیز به رسم نمودار برای داده‌های واقعی و پیش‌بینی گذشته، حال و آینده سری زمانی با در نظر گرفتن فاصله اطمینان ۹۵٪ و ۹۹٪ می‌پردازیم.

خروجی به صورت نمودار زیر نمایش داده می‌شود. واضح است که با افزایش درصد اطمینان، طول بازه اطمینان افزایش می‌یابد. از طرفی مقدارهای پیش‌بینی شده برای گذشته و همچنین برای ۲۱ روز آینده نوسانات کمی نسبت به نوسانات مقدارهای واقعی دارند.

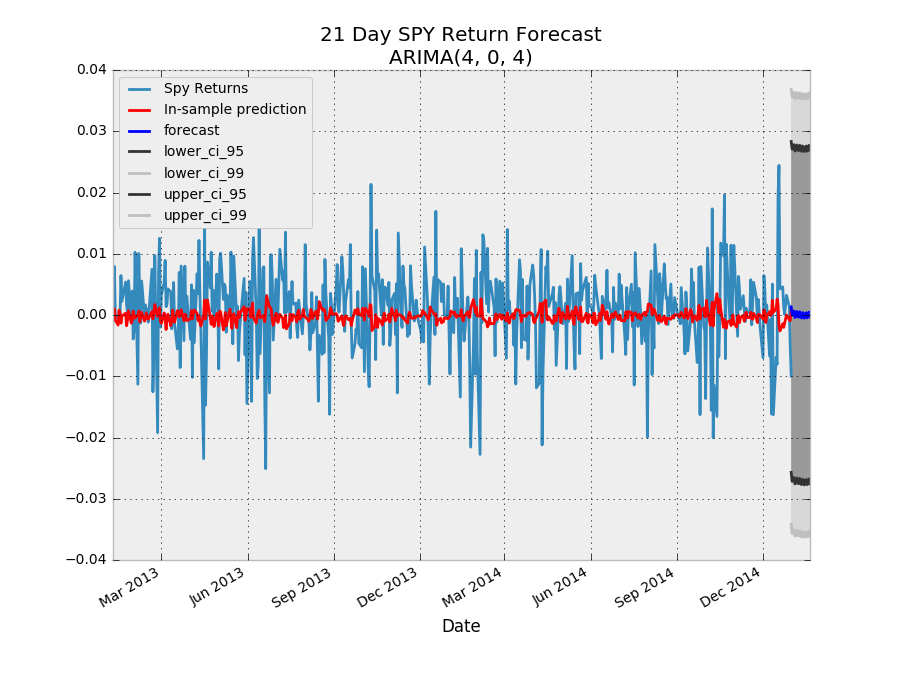
برای واقعی‌تر شدن پیش‌بینی‌های سری زمانی SPY بهتر است مدل را توسعه داده تا به نتایج واقعی‌تری برسیم.

مدل واریانس ناهمسانی شرطی اتورگرسیو

اگر به نظر برسد که مدل دارای شرایط واریانس ناهمسان است، به کارگیری مدل «واریانس ناهمسانی شرطی اتورگرسیو» (Autoregressive Conditionally Hetrosledastic Model) که به صورت نمادین $$ARCH(p)$$ نشان داده می‌شود مناسب‌ است.

فیلم آموزش سری های زمانی فصلی (رایگان) در فرادرس

کلیک کنید

این مدل را می‌توان توسعه‌ای روی مدل $$AR(p)$$‌ در نظر گرفت که روی واریانس سری زمانی اعمال می‌شود. به بیان دیگر مدل $$ARCH$$ مدلی برای مشخص کردن واریانس سری در زمان $$t$$ به شرط مشخص بودن وضعیت سری در زمان $$t-1$$ است. بنابراین مدل ریاضی آن را به صورت زیر می‌نویسیم.

$$\large \operatorname {Var}(y_t|y_{t-1})=\sigma^2_t=a_0+a_1y^2_{t-1}$$

اگر میانگین سری برابر با صفر باشد می‌توان مدل را به صورت زیر در نظر گرفت.

$$\large y_t=\sigma_t\varepsilon_t, \;\;\sigma_t=\sqrt{a_0+a_1y^2_{t-1}}, \;\;\varepsilon_t \sim N(0,1), iid$$

در ادامه براساس مدل $$ARCH(1)$$ یک نمونه ۱۰۰۰ تایی تولید می‌کنیم. توجه داشته باشید که در اینجا $$a_0=2 , a_1=0.5$$ در نظر گرفته شده است.

در کد بالا، نمودار تحلیل سری زمانی tsplot برای داده‌های شبیه‌سازی شده ترسیم شده است. در ادامه می‌توانید این نمودارها را مشاهده کنید.

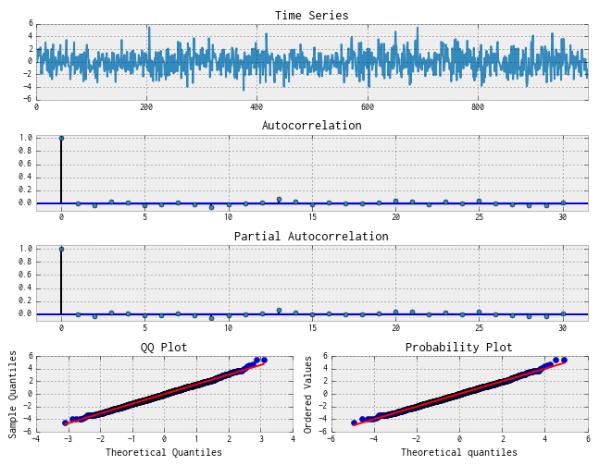
همین کار را برای داده‌های $$y^2_t$$ نیز انجام داده‌ایم که در واقع همان سری زمانی واریانس داده‌ها است. نمودارها مطابق با تصویرهای زیر هستند.

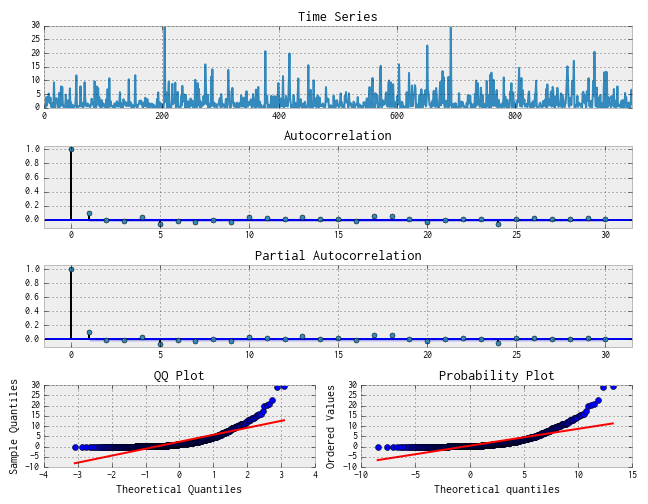
توجه کنید که در این حالت نیز ACF و PACF بعد از تاخیر ۱، برابر با صفر هستند که نشانگر مدل $$AR(1)$$ برای واریانس سری زمانی است.

مدل تعمیم یافته واریانس ناهمسانی شرطی اتورگرسیو

اگر مدل $$ARCH$$ را همان مدل $$AR$$ برای واریانس سری زمانی در نظر بگیریم، مدل $$GARCH$$ - مخفف Generalized Autoregressive Conditionally Heteroskedastic Models - نیز مدل $$ARMA$$ برای واریانس سری زمانی خواهد بود. بنابراین به نظر می‌رسد که پارامترهای مدل $$GARCH$$ به صورت $$p$$ و $$q$$ باشند. به این ترتیب می‌توان برای مدل $$GARCH(1,1)$$ رابطه‌های زیر را در نظر گرفت.

$$\large \varepsilon_t=\sigma_tw_t,\;\;\; \sigma^2_t=a_0+a_1\varepsilon^2_{t-1}+b_1\sigma^2_{t-1}$$

نکته: می‌دانید که در این رابطه‌ها $$w_t$$ همان نویز سفید است و $$a$$ و $$b$$ نیز پارامترهای مدل هستند. در مدل GARCH باید $$a_1+b_1\leq 1$$ در غیر اینصورت مدل پایدار نخواهد بود. در برنامه زیر مدل $$GARCH(1,1)$$ را شبیه‌سازی کرده‌ایم.

توجه دارید که در این شبیه‌سازی $$a_0=0.2, a_1=0.5, b_1=0.3$$ در نظر گرفته شده است. تعداد نمونه‌های سری زمانی نیز برابر با ۱۰۰۰۰ تعیین شده. نتیجه اجرای برنامه، مطابق با تصویر زیر خواهد بود.

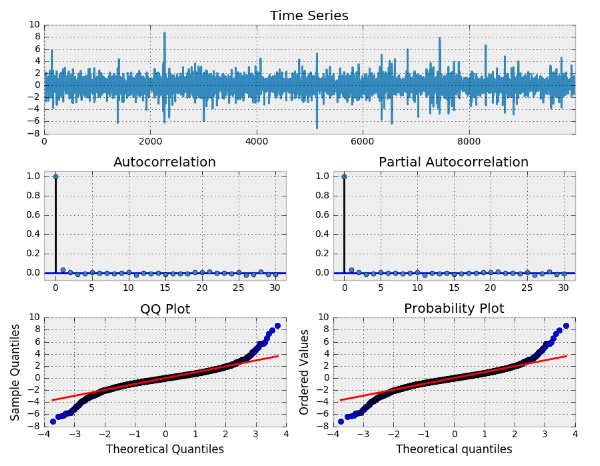
حال فرض کنید می‌خواهیم برای واریانس خطاها که در کد با eps مشخص شده است، تحلیل سری زمانی انجام دهیم. نمودارها به صورت زیر درخواهند آمد.

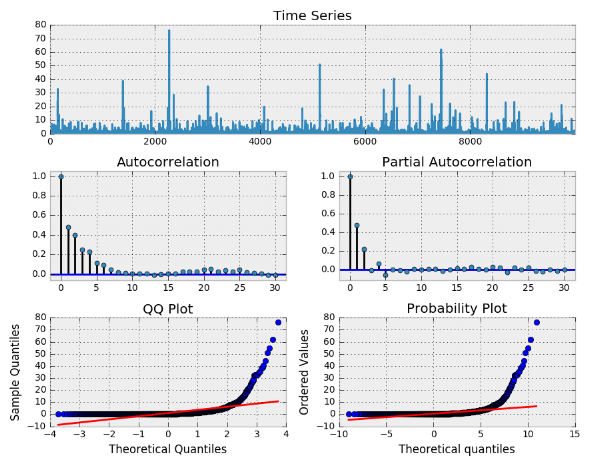
در نمودارهای ACF و PACF وجود خودهمبستگی به خوبی دیده می‌شود. بنابراین وجود هر دو مدل $$AR$$ و $$MA$$ ضروری به نظر می‌رسد. بنابراین با استفاده از تابع arch_model از بسته ARCH پارامترها را در کد‌های زیر برآورد می‌کنیم.

خروجی به صورت زیر در خواهد آمد.

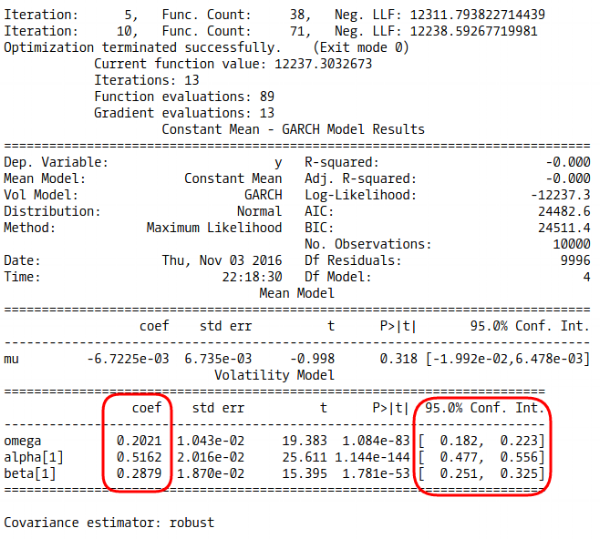
با توجه به مشخصاتی که برای مدل‌های جدید مورد بررسی قرار دادیم، برای تعیین مدل مناسب برای داده‌های SPY از مدل‌های معرفی شده مانند $$ARIMA$$ استفاده کرده و نتایج را در مدل $$GARCH$$ به کار خواهیم گرفت. روند کار به صورت زیر است.

• براساس مراحل تکراری مدل مناسب $$ARIMA(p,d,q)$$ را برازش داده و پارامترها را برآورد می‌کنیم.
• مدل $$GARCH$$ را با توجه به پارامترهای استخراج شده از مدل $$ARIMA$$ با کمترین AIC برازش می‌دهیم.
• باقی‌مانده‌های مدل حاصل را توسط تابع tsplot‌ مورد بررسی قرار می‌دهیم تا ایستا بودن مدل مشخص شود.

کدهای زیر به این منظور تهیه شده‌اند. البته با توجه به بازه زمانی که برای داده‌ها در نظر می‌گیرید ممکن است خروجی‌ها متفاوت باشد. در اینجا بازه از ۲۰۱۲ تا ۲۰۱۵ محسوب شده است.

به نظر می‌رسد مدل مناسب توسط معیار AIC با مرتبه‌های $$ARIMA(3,0,2)$$ خواهد بود.

$$\large aic:\; -5255.56673\; |\; order:\;(3, 0, 2)$$

نمودارهای tsplot‌ نیز در ادامه قابل مشاهده‌اند. به وضوح عدم خودهمبستگی توسط نمودارهای ACF و PACF دیده می‌شود. نرمال بودن باقی‌مانده‌ها نیز توسط نمودارهای Q-Q plot و P-P plot‌ مورد تایید است.

نمودارهای مربوط به واریانس باقی‌مانده نیز به مانند قبل ترسیم شده و قابل تفسیر هستند.

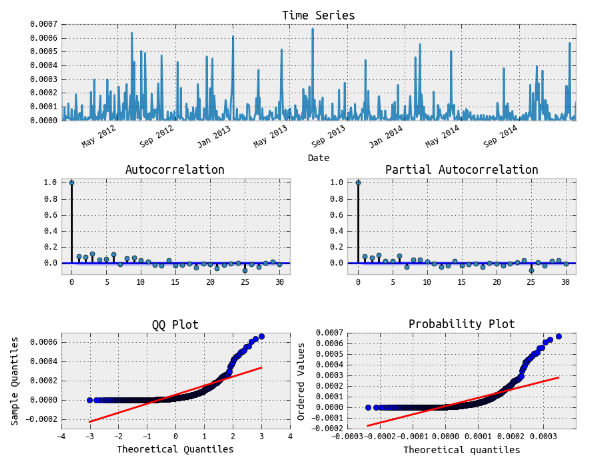
حال مدل $$GARCH$$ را برای داده‌های SPY‌ برازش می‌دهیم. پارامترهای مورد نظر یعنی p,q در ادامه برآورد می‌شوند.

خروجی به مانند تصویر زیر ساخته خواهد شد و در آن مقدار برآورد برای پارامترها و مقدار AIC‌ مدل قابل مشاهده است.

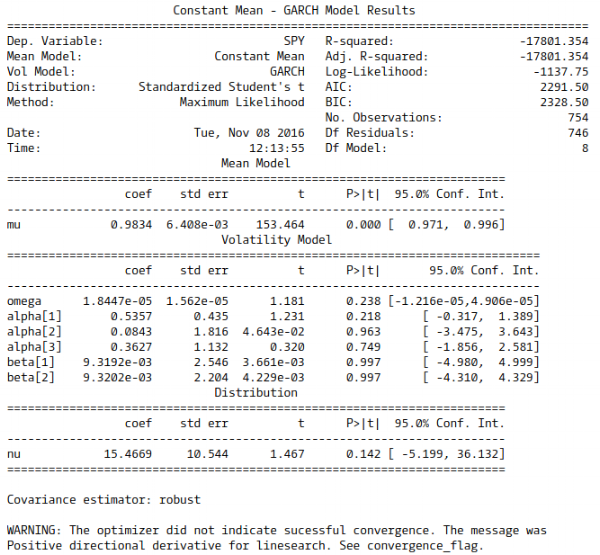
به منظور بررسی وضعیت باقی‌مانده‌ها نیز نمودارهای tsplot را رسم کرده‌ایم. همانطور که می‌بینید همه نمودارها به شکلی هستند که ایستایی را نشان می‌دهند.

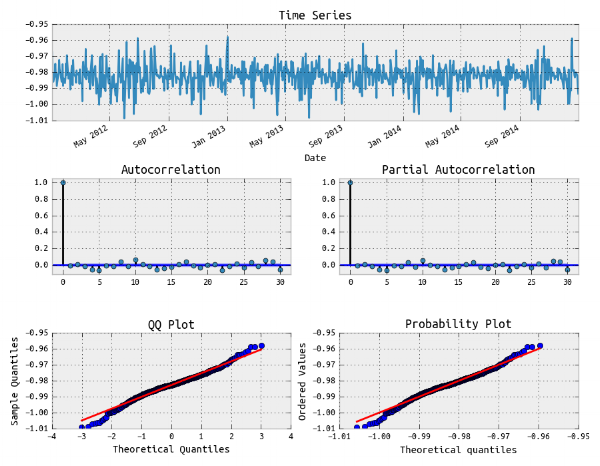
نرمال بودن باقی‌مانده‌ها نیز در نمودارهای مربوطه کاملا واضح است. نمودارهای ACF و PACF که در ادامه قابل مشاهده هستند، به خوبی عدم خودهمبستگی واریانس باقی‌مانده‌ها را نشان می‌دهند.

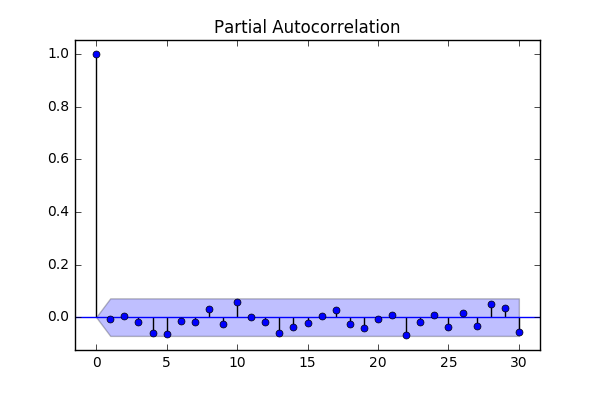
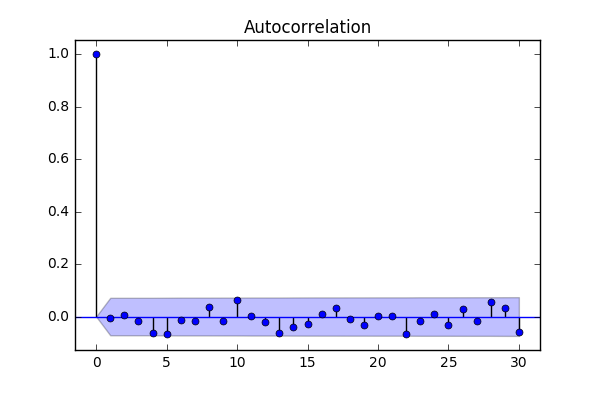
در قسمت‌ اول از این دنباله مقالات، به معرفی مفاهیم اولیه و مدل‌های پایه برای سری زمانی پرداختیم. در قسمت دوم نیز بررسی مدل‌هایی پرداختیم که ایستا هستند. سپس برای سری‌های زمانی ناایستا به دنبال تبدیلاتی گشتیم که آن‌ها را تبدیل به مدل‌هایی ایستایی کنند. در قسمت سوم و آخر نیز به مدل‌های ترکیبی پیچیده در مبحث سری‌های زمانی پرداخته شد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های پیش‌بینی و تحلیل سری‌های زمانی
• آموزش تحلیل و پیش‌بینی سری های زمانی
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش های کاربردی شبکه های عصبی مصنوعی
• سری زمانی در علم داده — از صفر تا صد
• تحلیل سری زمانی — تعریف و مفاهیم اولیه

^^