تعیین عکس العمل های تکیه گاهی تیرها — مثال های کاربردی

در بخش‌های قبلی شما را با انواع تیر، انواع تکیه‌گاه، نحوه تعیین عکس‌العمل‌های تکیه‌گاهی، انواع بار و انواع رهاساز آشنا کردیم. در این بخش به منظور آشنایی بیشتر با مفاهیم ارائه شده و نحوه تحلیل تیرها در شرایط گوناگون، به تشریح سه مثال خواهیم پرداخت. علاوه بر این، تأثیر رهاسازهای محوری، برشی و گشتاوری در تحلیل سازه‌ها را نیز مورد بررسی قرار می‌دهیم. به خاطر داشته باشید که در تحلیل سازه‌های دارای رهاساز، نمودار جسم آزاد سازه مورد بررسی در محل قرارگیری این نوع اتصالات برش داده می‌شود. به این ترتیب، یک معادله تعادل بیشتر برای تعیین عکس‌العمل‌های تکیه‌گاهی مجهول در نمودار جسم آزاد به دست می‌آید.

مثال 1

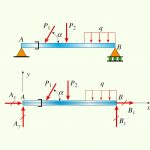
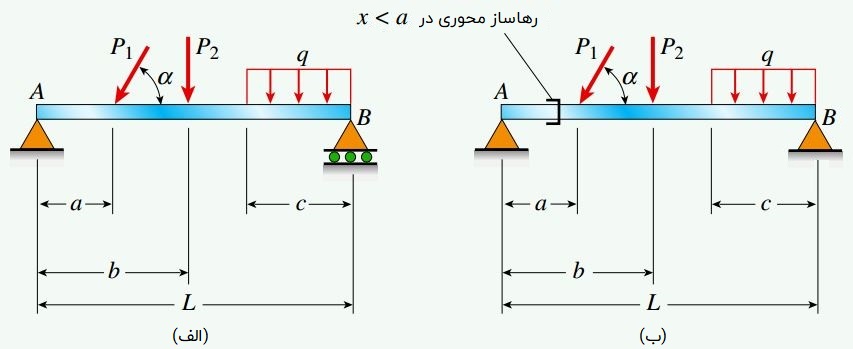
در شکل زیر دو تیر با تکیه‌گاه ساده نمایش داده شده است. تیر الف، توسط یک تکیه‌گاه لولایی در نقطه A و یک تکیه‌گاه غلتکی در نقطه B نگهداری می‌شود. نگهداری تیر ب نیز توسط دو تکیه‌گاه لولایی در نقاط A و B صورت می‌گیرد.

فیلم آموزش مقاومت مصالح – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

در این تیر علاوه بر دو تکیه‌گاه لولایی، یک رهاساز محوری در سمت چپِ اعمال نیروی مورب P₁ قرار دارد. با توجه اطلاعات مسئله، عکس‌العمل‌های تکیه‌گاهی تیرهای نمایش داده شده در شکل زیر را تعیین کنید.

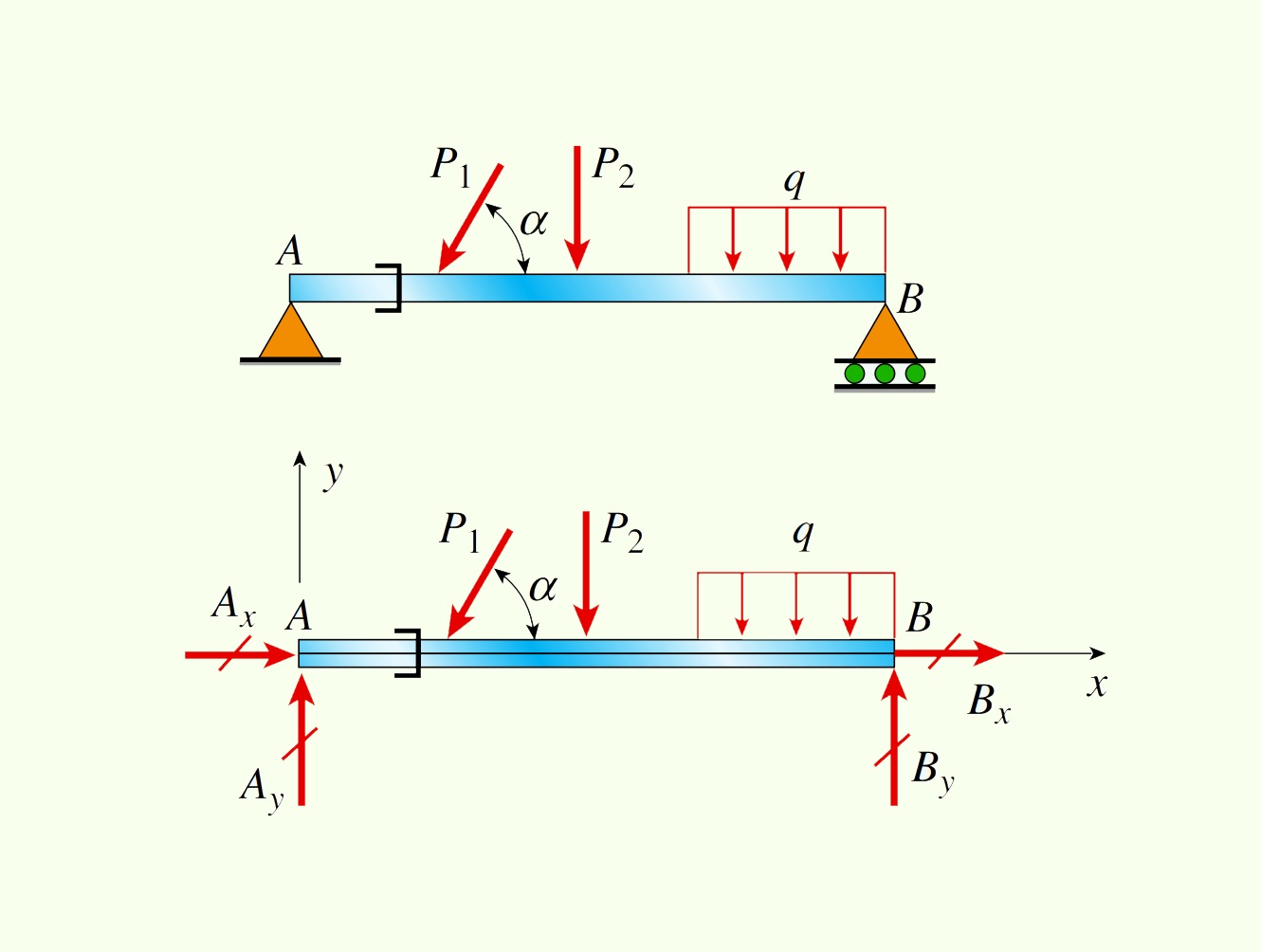
برای شروع تحلیل این مسئله، ابتدا نمودارهای جسم آزاد مربوط به هر یک از تیرها را رسم می‌کنیم. برای تیر الف، دو مؤلفه نیروی عکس‌العمل در نقطه A و یک مؤلفه در نقطه B وجود خواهد داشت. برای تیر ب، دو مؤلفه نیروی عکس‌العمل در هر یک از نقاط A و B اعمال خواهد شد.

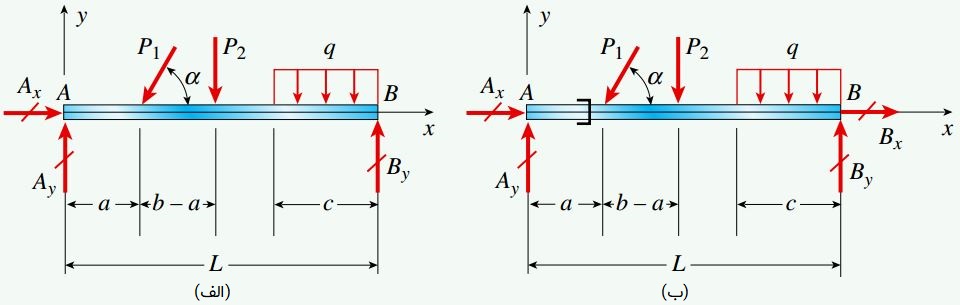
به دلیل وجود سه نیروی عکس‌العمل مجهول و همچنین سه معادله تعادل استاتیک در تیر الف، این سازه از نظر استاتیکی معین خواهد بود. وضعیت تیر ب کمی متفاوت است. چهار نیروی عکس‌العمل مجهول در این تیر وجود دارد. از این‌رو، به منظور دستیابی به یک معادله تعادل دیگر باید نمودار جسم آزاد آن را مطابق شکل زیر و در محل قرارگیری رهاساز به دو نمودار مجزا تقسیم می‌کنیم. به دلیل وجود رهاساز محوری، نیروی محوری N در مقطع مورد نظر برابر با صفر خواهد بود. به این ترتیب، معادله چهارم مورد نیاز برای تعیین تمام مجهولات مسئله به دست می‌آید.

عکس‌العمل‌های خارجی تیر الف

یکی از روش‌های ممکن برای به دست آوردن عکس‌العمل‌های تیر الف، به صورت زیر است:

عکس‌العمل‌های خارجی تیر ب

روابط به دست آمده برای تعیین A_y و B_y در بخش قبلی را می‌توان برای تیر ب نیز مورد استفاده قرار داد. به منظور تعیین دیگر مجهولات مسئله، از نمودارهای جسم آزاد مجزا (نمودارهای سمت چپ و راس ت تیر) استفاده می‌کنیم:

بر اساس نتایج به دست آمده می‌توان مشاهده کرد که با قرار دادن یک تکیه‌گاه لولایی به جای تکیه‌گاه غلتکی تیر الف، این سازه از نظر استاتیکی نامعین می‌شود. با این وجود، در صورت افزودن یک رهاساز نیروی محوری به مدل، امکان تحلیل سازه با استفاده از قوانین استاتیکی فراهم خواهد شد. دلیل این امر، به دست آمدن یک معادله تعادل اضافی مربوط به رهاساز است.

مثال 2

دو تیر نمایش داده شده در شکل زیر را در نظر بگیرید. تیر الف توسط یک تکیه‌گاه لولایی در نقطه A و یک تکیه‌گاه غلتکی در نقطه B نگهداری می‌شود. نگهداری تیر ب نیز توسط یک تکیه‌گاه لولایی در نقطه A و دو تکیه‌گاه غلتکی در نقاط B و C صورت می‌گیرد.

فیلم آموزش مقاومت مصالح 1 و 2 – مرور و حل مساله در فرادرس

کلیک کنید

به علاوه، در سمت چپ تکیه‌گاه B نیز یک رهاساز برشی وجود دارد. با توجه به اطلاعات موجود در شکل، عکس‌العمل‌های تکیه‌گاهی هر یک از تیرها را تعیین کنید.

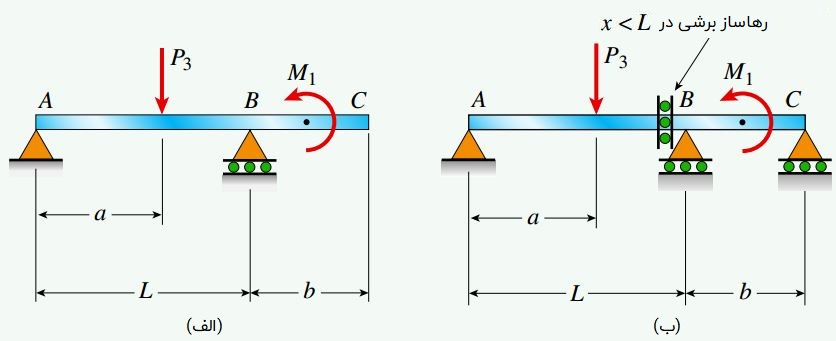
شکل زیر، نمودارهای جسم آزاد تیرهای الف و ب را نمایش می‌دهد. در تیر الف، سه مؤلفه نیروی عکس‌العمل (دو مؤلفه در نقطه A و یک مؤلفه در نقطه B) وجود دارد. در تیر ب نیز مجموعاً چهار مؤلفه نیروی عکس‌العمل (دو مؤلفه در نقطه A، یک مؤلفه در نقطه B و یک مؤلفه در نقطه C) اعمال می‌شود.

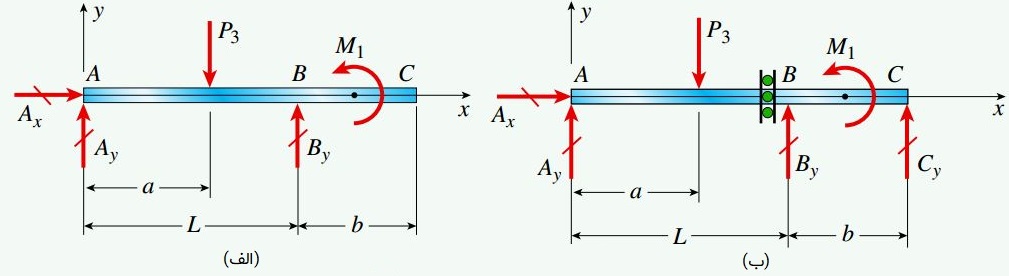
به دلیل وجود سه نیروی عکس‌العمل مجهول و سه معادله تعادل استاتیکی در تیر الف، این سازه از نظر استاتیکی معین خواهد بود. در طرف مقابل، تیر ب دارای چهار نیروی عکس‌العمل مجهول است اما تنها سه معادله تعادل از نمودار جسم آزاد آن به دست می‌آید. به همین دلیل، این سازه از نظر استاتیکی نامعین در نظر گرفته می‌شود. اگر نمودار جسم آزاد تیر ب را مطابق شکل زیر در محل رهاساز برشی به دو قسمت تقسیم کنیم، به یک معادله تعادل اضافی دست خواهیم یافت؛ چراکه در محل این رهاساز، نیروی برشی V برابر با صفر است.

عکس‌العمل‌های خارجی تیر الف

اگر در نمودار جسم آزاد تیر الف، نیروهای موجود در راستای x را با هم جمع کنیم، A_x به دست می‌آید.

فیلم آموزش استاتیک – مرور و حل تست کنکور ارشد مهندسی مکانیک در فرادرس

کلیک کنید

به منظور تعیین B_y باید گشتاورهای به دست آمده حول نقطه A و برای مشخص کردن A_y نیز باید گشتاورهای به دست آمده حول B را با هم جمع کنیم:

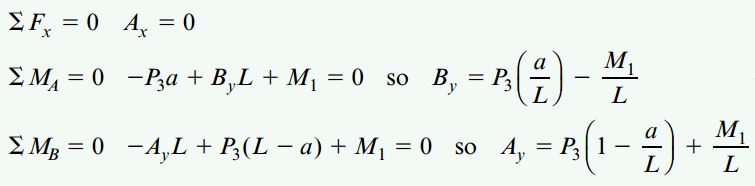
عکس‌العمل‌های خارجی تیر ب

برای تعیین A_y و B_y در تیر ب می‌توانیم از نمودارهای جسم آزاد مجزای این سازه استفاده کنیم:

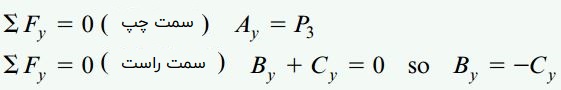
با توجه به نمودار جسم آزاد کلی این تیر، مجهولات دیگر مسئله نیز به دست می‌آیند:

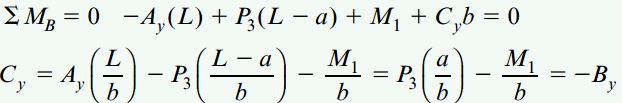
توجه: به طور کلی، اگر یک تیر دارای یک رهاساز داخلی باشد، به منظور تعیین تمام عکس‌العمل‌های تکیه‌گاهی باید با ایجاد یک مقطع در محل رهاساز، نمودار جسم آزاد تیر را به دو نمودار مجزا تقسیم کرد.

مثال 3

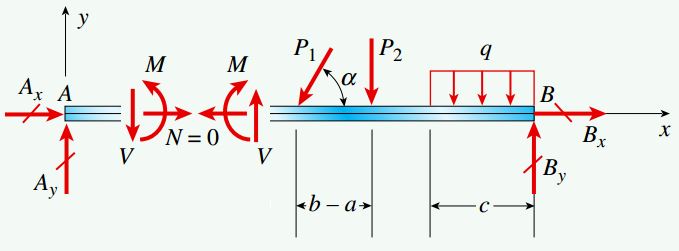
شکل زیر، دو تیر با شرایط مختلف را نمایش می‌دهد. تیر یکسر گیردار الف در معرض یک بار متمرکز مورب (P₄) و یک بار گسترده متغیر قرار گرفته است.

فیلم آموزش مقاومت مصالح – ویژه رشته عمران در فرادرس

کلیک کنید

بارهای اعمال شده بر روی تیر ب نیز مشابه تیر الف هستند؛ با این تفاوت که یک اتصال لولایی (رهاساز گشتاوری) در سمت راست تکیه‌گاه A و یک تکیه‌گاه غلتکی در نقطه B وجود دارد.

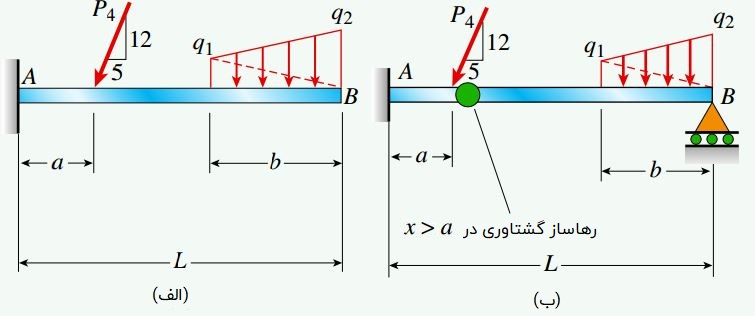
نمودارهای جسم آزاد هر یک از تیرها در شکل زیر نمایش داده شده‌اند. تیر الف دارای سه مؤلفه عکس‌العمل در نقطه A (دو مؤلفه نیرو و یک مؤلفه گشتاور) است. در تیر ب، علاوه بر این سه مؤلفه، یک مؤلفه نیروی عکس‌العمل نیز در تکیه‌گاه غلتکی B وجود دارد.

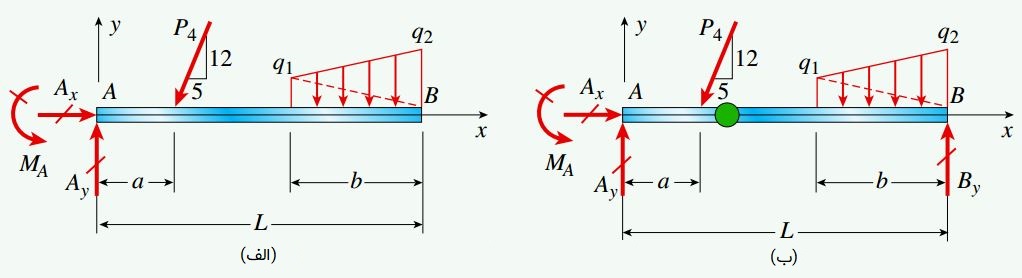
با توجه به نمودار جسم آزاد تیر الف می‌توان دریافت که این سازه از نظر استاتیکی معین است (وجود سه مجهول و سه معادله). در طرف مقابل، تیر ب مانند مثال‌های قبلی یک مجهول بیشتر دارد. از این‌رو، برای تعیین مجهولات مسئله تنها با استفاده از پیکربندی تیر، به یک معادله دیگر نیز نیاز خواهد بود. دستیابی به این معادله با تقسیم نمودار جسم آزاد تیر ب به دو نمودار مجزا امکان‌پذیر می‌شود. به دلیل وجود رهاساز گشتاوری، مقدار گشتاور موجود در محل قرارگیری رهاساز برابر با صفر است. این موضوع، معادله تعادل مورد نیاز برای تعیین هر چهار مؤلفه عکس‌العمل در تیر ب را فراهم می‌کند.

عکس‌العمل‌های خارجی تیر الف

با جمع نیروهای موجود در راستای x، نیروهای موجود در راستای y و گشتاورهای حول نقطه A، روابط مورد نیاز برای تعیین عکس‌العمل‌های تکیه‌گاه A به دست می‌آیند. با تقسیم ذوزنقه معرف بار گسترده به دو مثلث جداگانه (مطابق شکل بالا) می‌توانیم برآیند هر یک از مثلث‌ها را با برآیند بار آن‌ها جایگزین کنیم. این برآیندها با مساحت مثلث مربوط به خود برابر هستند که از مرکز هندسی از آن عبور می‌کنند. به این ترتیب:

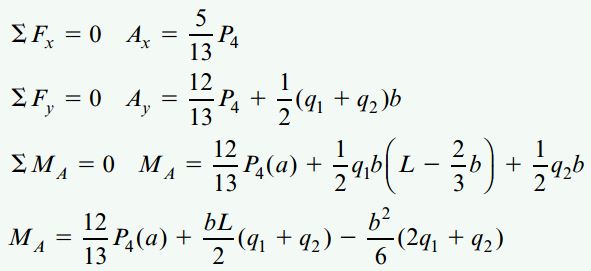
عکس‌العمل‌های خارجی تیر ب

در ابتدا توجه داشته باشید که رابطه عکس‌العمل A_x در هر دو تیر با هم برابر هستند. با در نظر داشتن این موضوع، روابط مورد نیاز برای محاسبه عکس‌العمل‌های دیگر را به دست می‌آوریم. اگر نمودار جسم آزاد تیر ب را در محل رهاساز گشتاوری به دو نمودار مجزا تقسیم کرده و گشتاورهای نمودار سمت راست را با هم جمع کنیم، خواهیم داشت:

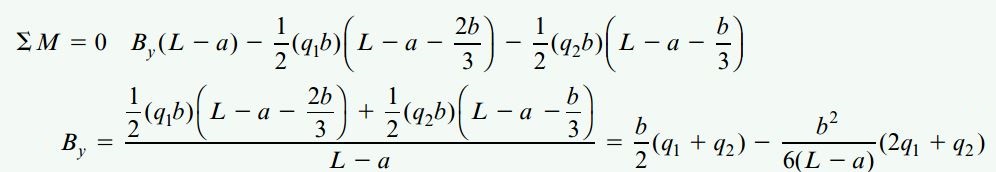
در مرحله بعد، با جمع نیروهای موجود در راستای y برای نمودار جسم آزاد کل تیر نیز به رابطه زیر می‌رسیم:

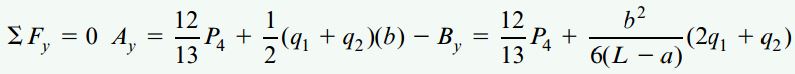
در نهایت، با جمع گشتاورهای حول نقطه A در نمودار جسم آزاد کل تیر، رابطه زیر را به دست می‌آوریم:

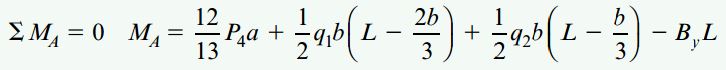
فرم ساده‌شده رابطه بالا به صورت زیر نوشته می‌شود:

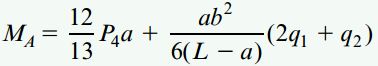
توجه: استفاده از راه حل‌های پارامتری، روش مناسبی برای نمایش مراحل مورد نیاز برای تحلیل مسائل مربوط به عکس‌العمل‌های تکیه‌گاهی است. علاوه بر این، به خاطر داشته باشید که به کارگیری نمودارهای جسم آزاد در مثال‌های بالا، به حل سریع‌تر و راحت این‌گونه مسائل کمک می‌کند.

^^