سرعت صوت و معادلات مربوط به موج صوتی — از صفر تا صد

به میزان مسافت پیموده شده در واحد زمان، توسط امواج صوتی، در یک محیط الاستیک، «سرعت صوت» (Speed of Sound) گفته می‌شود. این سرعت در هوای صفر درجه برابر با 331.2 متر بر ثانیه است. زمانی که دمای هوا 20 درجه باشد، این سرعت برابر با 343 متر بر ثانیه خواهد بود.

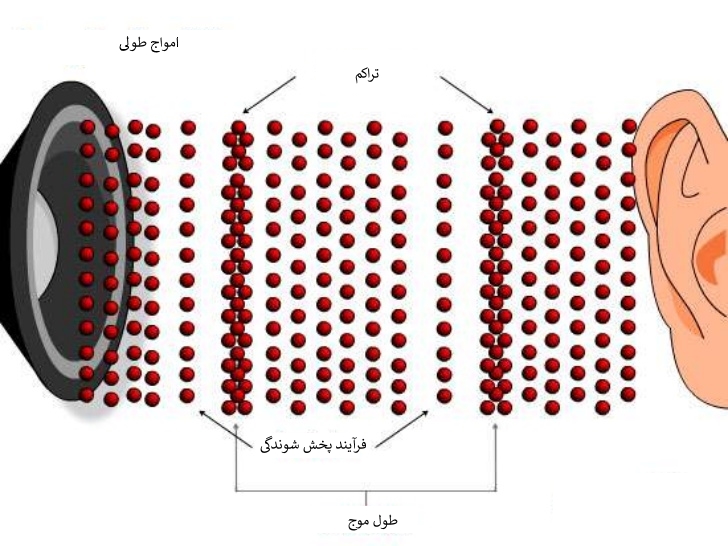
سرعت صوت در یک گاز ایده‌آل فقط به دمای آن و ترکیب گاز مربوطه وابسته است. لازم است بدانید که به منظور محاسبه سرعت در هوای معمولی می‌توان آن را گاز کامل در نظر گرفت. در مکالمات روزمره عمدتا سرعت صوت بیان کننده سرعت هوا است؛ اما واقعیت این است که حتی در جامدات نیز این سرعت قابل تعریف است. توجه داشته باشید که سرعت صوت در گازها کمتر از مایعات و در جامدات بیشتر از آن است. برای مثال سرعت صوت در هوای معمولی برابر با 343، در آب 1484 و در الماس برابر با 5120 متر بر ثانیه است.

امواج صوتی در جامدات، ترکیبی از امواج‌های فشاری و برشی محسوب می‌شوند. امواج فشاری در جامدات، با استفاده از تعریف پارامترهایی هم‌چون تراکم‌پذیری، مدول برشی و چگالی، قابل بیان هستند. بسیار مهم است بدانید که سرعت هر سیالی در محیط، نسبت به سرعت صوت در همان محیط سنجیده می‌شود؛ بدین منظور از عددی بی‌بعد تحت عنوان «عدد ماخ» (Mach Number) استفاده می‌شود.

مفاهیم پایه

به منظور توضیح مفهوم انتقال امواج صوتی از مدل مبتنی بر آرایه‌ای از کره استفاده می‌شود که به وسیله تعدادی فنر به یکدیگر متصل شده‌اند. در یک جسم واقعی، کره‌ها همان مولکول‌ها و فنرها پیوند‌های میان آن‌ها هستند. امواج صوتی با استفاده از نوسان طولی این فنر‌ها مدل‌سازی می‌شوند.

فیلم آموزش فیزیک پایه ۳ در فرادرس

کلیک کنید

صوت در یک محیط، با استفاده از انتقال انرژی ناشی از منقبض و منبسط شدن فنرها به مولکول‌های اطراف، مدل‌سازی می‌شود. سرعت صوت در این مدل، به سختی فنرهای فرض شده و جرم کره‌ها وابسته است.

تا زمانی که فاصله کره‌ها ثابت بماند، سختی فنر بزرگ‌تر منجر به انتقال انرژی بیشتر می‌شود و جرم کره زیادتر، انتقال انرژی کمتر را در پی خواهد داشت. در یک ماده واقعی، سختی فنر تحت عنوان «مدول الاستیک» و جرم ماده در قالب «چگالی» بیان می‌شوند.

همان‌طور که قبلا نیز ذکر شد، سرعت صوت در مواد سخت‌تر، بیشتر نیز خواهد بود. به عنوان نمونه این سرعت در نیکل 1.59 برابر برنز است. از طرفی این مقدار با افزایش چگالی، کاهش می‌یابد. به عنوان نمونه سرعت صوت در هیدروژن سبک، 1.41 برابر سرعت صوت در هیدروژن سنگین است. دلیل این امر چگال‌تر بودن دوتریوم نسبت به پروتیوم است.

دقت کنید که در بعضی از متون علمی به اشتباه به این مورد اشاره شده که سرعت صوت در سیال چگال بیشتر از سیال سبک است.

امواج فشاری و برشی

همان‌طور که قبلا نیز بیان شد، امواج صوتی در سیالات گازی فقط در قالب امواج فشاری منتقل می‌شوند؛ اما در جامدات، این انتقال همزمان به صورت برشی و فشاری صورت می‌گیرد. یک موج طولی اشاره به موجی دارد که به صورت پیوسته و در راستای انتشار موج، منقبض و منبسط می‌شود. نوع دوم امواج که فقط در جامدات رخ می‌دهند، اموج عرضی (موج برشی) هستند.

فیلم آموزش فیزیک ۳ – حل تمرین در فرادرس

کلیک کنید

در بعضی از موارد، این دو نوع از امواج دارای سرعت‌های متفاوتی هستند. در این حالات، امواج با زمان‌های متفاوتی به ناظر خواهند رسید. یک مثال واضح از این مفهوم، زلزله است. هنگام رخ دادن یک زلزله در ابتدا امواج طولی شنیده می‌شوند، سپس امواج عرضی ظاهر خواهند شد.

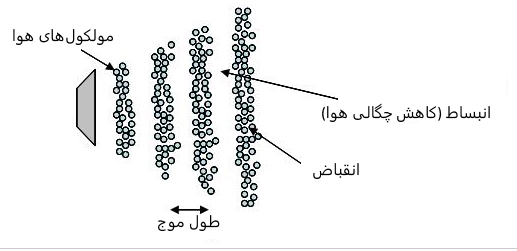
در حالت کلی، سرعت انتشار یک موج در محیط، با استفاده از چگالی و تراکم‌پذیری محیط مد نظر، تعیین می‌شود. آنالیز این سرعت در جامدات همانند سیالات است با این تفاوت که فاکتوری تحت عنوان «مدول برشی» (Shear module) نیز مد نظر قرار داده می‌شود. توجه داشته باشید که این فاکتور، فقط امواج طولی را تحت تاثیر قرار می‌دهد. بنابراین سرعت انتشار امواج برشی در جامدات، با استفاده از دو فاکتور مدول برشی و چگالی محیط، قابل محاسبه هستند.

معادلات مربوط به موج صوتی

سرعت صوت در متون علمی با حرف «c» نشان داده می‌شود. [c حرف اول کلمه لاتین Celeritas به معنای صوت است.

فیلم آموزش امواج و ارتعاشات در فرادرس

کلیک کنید

سرعت صوت در گازها با استفاده از فرمول عمومی نیوتن-لاپلاس و به صورت زیر قابل محاسبه است.

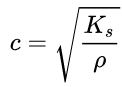
در این معادله، Ks ضریب سختی گاز و ρ چگالی آن است. همان‌طور که در معادله نیز می‌بینید، سرعت صوت با ازدیاد سختی، افزایش و با افزایش چگالی، کاهش می‌یابد. برای گاز‌های ایده‌آل، مدول بالک K را می‌توان با ضرب کردن فشار آن در «شاخص بی‌دررو» محاسبه کرد. این حاصل ضرب برای هوا در شرایط استاندارد، برابر با 1.4 است.

قالب کلی معادله سرعت صوت به شکل زیر بیان می‌شود.

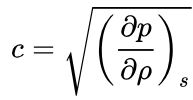
در این معادله، p فشار سیال و ρ چگالی آن است. [توجه شود که مشتق‌گیری از این معادله به صورت انتروپی ثابت (آیزنتروپیک) گرفته می‌شود.] با فرض در نظر گرفتن تاثیرات نسبیتی، سرعت صوت را می‌توان با استفاده از «معادله نسبیتی اویلر» (Relativistic Euler equation) محاسبه کرد.

روابط محاسبه سرعت صوت در هوای خشک

در اکثر مسائل تئوری و مهندسی با سرعت صوت در هوا سر و کار داریم. از رابطه زیر می‌توان به منظور محاسبه سرعت صوت در هوای خشک (0 درصد رطوبت) که در دمای نزدیک به صفر درجه قرار گرفته، استفاده کرد.

فیلم آموزش آیرودینامیک ۱ در فرادرس

کلیک کنید

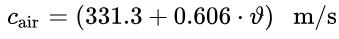
در این رابطه، ν دما (بر حسب درجه) است. معادله بیان شده در واقع دو عبارت اول بسط تیلورِ رابطه زیر است.

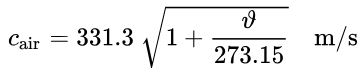
سرعت صوت در گاز‌های ایده‌آل

برای یک گاز ایده‌آل فاکتوری تحت عنوان K تعریف می‌شود که آن را «مدول بالک» (Bulk Module) می‌نامند. در مواد جامد، این مقدار همان ضریب سختی جامد (C) است. در حالت کلی مدول بالک با استفاده از رابطه زیر محاسبه می‌شود.

فیلم آموزش مفاهیم مقدماتی آیرودینامیک (رایگان) در فرادرس

کلیک کنید

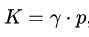
با جایگذاری این مقادیر در معادله نیوتن-لاپلاس اشاره شده در بالا، سرعت صوت در یک گاز ایده‌آل به صورت زیر به دست می‌آید.

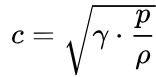
در این معادله، γ شاخص بی‌دررو یا «فاکتور انبساط آیزنتروپیک» است. در یک گاز ایده‌آل، مدول بالک معادل با نسبت C_p/C_v در نظر گرفته می‌شود. همچنین در این معادله، p برابر با فشار و ρ به عنوان چگالی سیال در نظر گرفته می‌شوند. با استفاده از جایگذاری MRT/V به جای p، می‌توان قانون گاز ایده‌آل را در معادله بالا اعمال کرد.

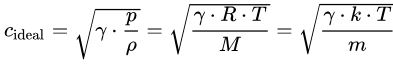
در این معادله، k ثابت بولتزمن، γ شاخص بی‌دررو سیال و R، ثابت عمومی گاز‌ها (برابر با 8.314) هستند. هم‌چنین T دمای مطلق سیال است که در قالب کلوین بیان می‌شود.

عدد ماخ

در دینامیک سیالات، عدد ماخ مقداری بی بعد است که به صورت نسبت سرعت سیال به سرعت محلی صوت در آن محیط، تعریف می‌شود. بنابراین عدد ماخ M، برای سیالی با سرعت u برابر است با:

فیلم آموزش آیرودینامیک ۱ در فرادرس

کلیک کنید

در این معادله، M عدد ماخ، u سرعت محلی سیال و c سرعت صوت در سیال مد نظر هستند. بر مبنای این تعریف عدد ماخ کمتر از 1 سرعت «مادون صوت» (Subsonic) و بیشتر از آن، سرعت «فراصوت» (Super Sonic) را نشان می‌دهد. عدد ماخ، معیاری از میزان تراکم‌پذیری سیال در نظر گرفته می‌شود. این عدد پارامتر بسیار مهمی در طراحی ماشین‌های پرنده، خصوصاً جنگنده‌های مافوق صوت است.

معمولاً در مواردی که سرعت سیال به طور ناگهانی از ناحیه فراصوت به مادون صوت تغییر می‌کند، پدیده‌ای تحت عنوان «موج ضربه‌ای» (Shock Wave) اتفاق می‌افتد. از نظر ترمودینامیکی این پدیده کاملا برگشت‌ناپذیر است. توجه داشته باشید که موج ضربه‌ای، منجر به تغییر ناگهانی فشار و دما در اطراف مرز جسم جامد خواهد شد.

در صورتی که مطلب بالا برای شما مفید بوده است، احتمالا آموزش‌هایی که در ادامه آمده‌اند نیز برایتان کاربردی خواهند بود.

• عدد ماخ -- به زبان ساده
• آموزش مکانیک سیالات
• آموزش ترمودینامیک
• ترمودینامیک -- از صفر تا صد