تحلیل پایداری شیب با استفاده از روش های تعادل حدی (Limit Equilibrium Methods)
«روش تعادل حدی» (Limit Equilibrium Method) یا اصطلاحاً «LEM»، سادهترین و متداولترین گزینه برای اجرای تحلیل پایداری شیب است. در روشهای تعادل حدی، احتمال لغزش توده سنگ یا خاک بر اثر نیروی جاذبه مورد بررسی قرار میگیرد. مبنای تمام این روشها، مقایسه نیروهای مقاوم (نیروها، گشتاورها یا تنشهای مقاوم در برابر حرکت توده) نسبت به نیروهای محرک (نیروها، گشتاورها یا تنشهای به وجود آورنده حرکت ناپایدار) است.
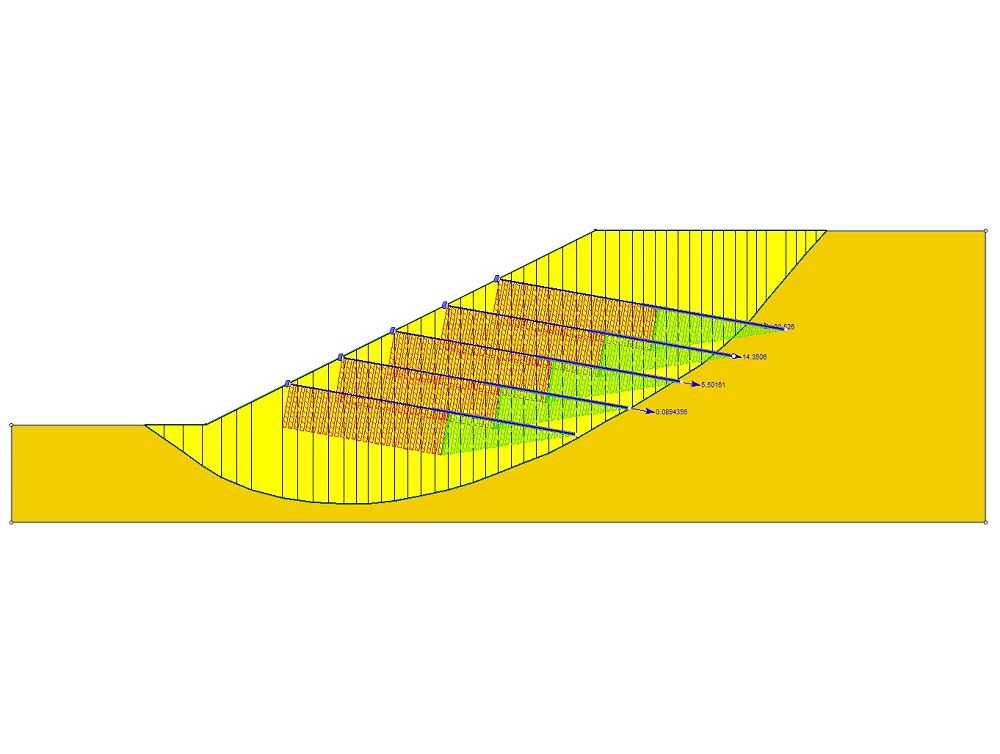
نوع حرکت سطح لغزش شیبهای سنگی یا خاکی در LEM به صورت «انتقالی» (Transitional) یا «دورانی» (Rotational) در نظر گرفته میشود. «ضریب ایمنی» (Factor of Safety) به عنوان یکی از خروجیهای اصلی تحلیلهای تعادل حدی به حساب میآید. این ضریب به صورت نسبت مقاومت برشی به تنش برشی تعریف میشود. اگر مقدار ضریب ایمنی کمتر از 1 باشد، شیب ناپایدار خواهد بود.
مقدمه
به طور کلی، روشهای مرسوم تحلیل پایداری شیب به سه گروه تحلیل سینماتیک، تحلیل تعادل حدی و شبیهسازهای ریزش سنگ تقسیم میشوند. اکثر برنامههای کامپیوتری تحلیل پایداری شیب بر اساس مفهوم تعادل حدی برای مدلهای دوبعدی و سهبعدی توسعه یافتهاند. در تحلیلهای دوبعدی از فرض کرنش صفحهای استفاده میشود.
اجرای تحلیل پایداری شیبهای دوبعدی با استفاده از رویکردهای تحلیلی ساده میتواند اطلاعات مهمی را برای طراحی اولیه و ارزیابی ریسک فراهم کند.
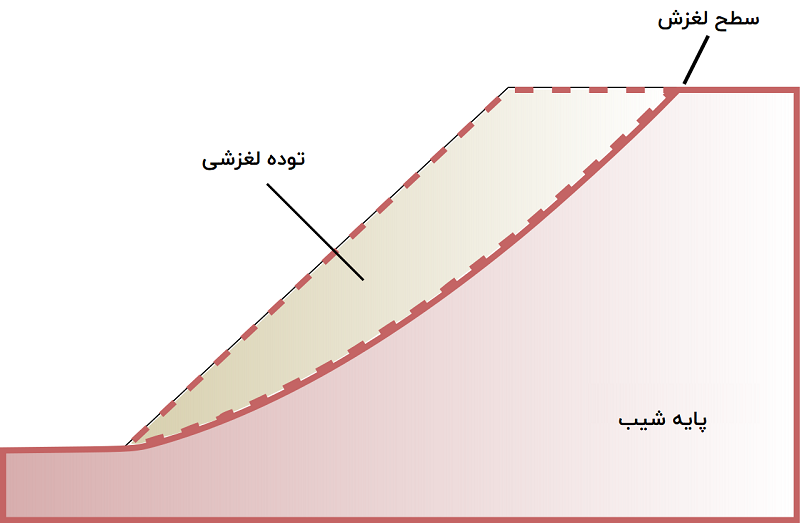
در تمام روشهای تعادل حدی فرض میشود که مقدار مقاومت برشی در امتداد سطح شکست احتمالی با استفاده از روابط خطی (مور-کولمب) یا غیرخطی بین این مقاومت و تنش نرمال سطح شکست قابل تعیین است. متداولترین رابطه در این زمینه، «تئوری ترزاقی» (Terzaghi's Theory) است:
τ: مقاومت برشی سطح؛ ′σ: تنش مؤثر (تنش نرمال کل منهای فشار آب منفذی)؛ ′ϕ: زاویه اصطکاک مؤثر؛ ′c: چسبندگی مؤثر
«روش قطعات» (Methods of Slices)، محبوبترین رویکرد در بین روشهای تعادل حدی است. در این رویکرد، توده خاک به چندین قطعه عمودی تقسیم میشود. این روش در حال حاضر چندین نسخه مختلف دارد. به دلیل فرضیات و شرایط مرزی متفاوت در هر نسخه، نتایج (ضریب ایمنی) هر یک از آنها نیز با هم متفاوت است.
ناحیه سطح شکست احتمالی در روشهای تعادل حدی معمولاً مشخص نیست اما میتوان موقعیت آن را با استفاده از روشهای بهینهسازی عددی تعیین کرد. به عنوان مثال، در «طراحی عملکردی شیب» (Functional Slope Design)، محلی که دارای کمترین ضریب ایمنی بین سطوح احتمالی باشد به عنوان ناحیه سطح لغزش بحرانی در نظر گرفته میشود. طیف گستردهای از نرمافزارهای تحلیل پایداری شیب، از مفهوم تعادل حدی به همراه تعیین خودکار سطح لغزش بحرانی استفاده میکنند.
نرمافزارهای معمولی تحلیل پایداری شیب میتوانند شیبهای خاکی لایهای، خاکریزها، گودبرداری و سازه نگهبان را مورد ارزیابی قرار دهند. علاوه بر این، تأثیرات زمینلرزه، بارگذاریهای خارجی، آبهای زیرزمینی، نیروهای مقاومساز (کابلهای مهاری و دیگر نگهدارندهها) را نیز در این نرمافزارها قابل محاسبه است.
روشهای تحلیلی: روش قطعات
بسیاری از ابزارهای تحلیل پایداری شیب، از نسخههای مختلف روش قطعات نظیر «بیشاپ ساده شده» (Bishop Simplified)، «روش معمولی قطعات» (Ordinary Method of Slices)، «اسپنسر» (Spencer)، «سارما» (Sarma) و غیره استفاده میکنند. به دلیل صدق کردن هر سه شرط تعادل (تعادل نیروی افقی، تعادل نیروی عمودی و تعادل گشتاور) در روشهای سارما و اسپنسر، این موارد به عنوان «روشهای دقیق» (Rigorous Methods) شناخته میشوند.
در طرف مقابل، روشهای بیشاپ ساده شده و «فلنیوس» (Fellenius)، تنها برخی از شرطهای تعادل را ارضا میکنند و فرضیات ساده را در نظر میگیرند. از اینرو، به آنها «روشهای غیر دقیق» (Non-rigorous Methods) میگویند. در ادامه، به توضیح برخی از این روشها می.
روش سوئدی دایره لغزش
در «روش سوئدی دایره لغزش» (Swedish Slip Circle Method) فرض میشود که زاویه اصطکاک خاک یا سنگ برابر با صفر است (τ′= c). به عبارت دیگر، هنگامی که زاویه اصطکاک برابر با صفر در نظر گرفته شود، عبارت حاوی تنش مؤثر نیز به سمت صفر میل میکند. بنابراین، مقاومت برشی با پارامتر چسبندگی ماده مورد نظر برابر میشود (به تئوری ترزاقی مراجعه شود).
روش سوئدی، سطح لغزش احتمالی را به صورت دایرهای در نظر میگیرد و پارامترهای مقاومتی و تنش را با استفاده از قواعد استاتیکی و هندسه دایرهای مورد تحلیل قرار میدهد. گشتاور ناشی از نیروهای محرک داخلی شیب با گشتاور ناشی از نیروهای مقاوم در برابر شکست شیب مقایسه میشوند. اگر نیروهای مقاوم بیشتر از نیروهای محرک باشند، شیب مورد نظر پایدار در نظر گرفته خواهد شد.
روش معمولی قطعات
در روش قطعات (OMS) یا فلنیوس، توده در حال لغزش (توده بالای سطح شکست) به چندین قطعه تقسیم میشود. نیروی اعمال شده به هریک از این قطعات با در نظر گرفتن تعادل مکانیکی (نیرو و گشتاور) آن قطعه به دست میآید. بر اساس فرضیات این روش، هر قطعه فقط وزن خود را تحمل میکند و هیچ فعل و انفعالی با قطعات دیگر ندارد؛ چراکه نیروهای برآیند با بخش زیرین هر قطعه موازی هستند.
با این وجود، قانون سوم نیوتون در این روش رعایت نمیشود؛ زیرا به طور کلی، نیروهای برآیند سمت راست و چپ هر قطعه دارای مقدار برابر و همچنین دارای امتداد یکسان نیستند.

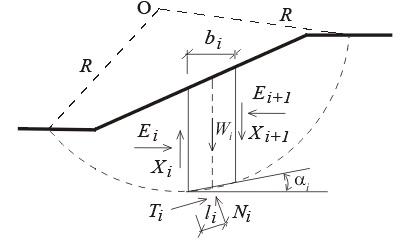
رویکرد اتخاذ شده در روش قطعات، تنها با در نظر گرفتن وزن خاک به همراه تنشهای نرمال و برشی در امتداد سطح شکست، امکان انجام یک محاسبه ساده برای تعیین تعادل استاتیکی شیب را فراهم میکند. برای هر قطعه میتوان زاویه اصطکاک و چسبندگی را نیز در نظر گرفت. در موارد کلی، نیروی وارده بر یک قطعه همانند شکل زیر نمایش داده میشود. نیروهای نرمال (Er,El) و برشی (Sr,Sl) موجود در بین قطعات مجاور، هر قطعه را محدود میکنند. به علاوه، با در نظر گرفتن این نیروها در محاسبات، مسئله از نظر استاتیکی نامعین میشود.
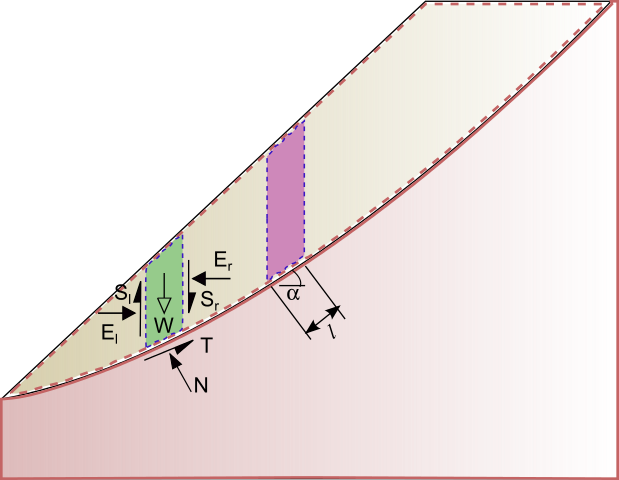
در شکل بالا فرض میشود که بلوک مورد بررسی دارای ضخامت b است. قطعات سمت چپ و راست، نیروهای نرمال El و Er و نیروهای برشی Sl و Sr را به قطعه مورد بررسی اعمال میکنند و وزن این قطعه، نیروی W را به وجود میآورد. این نیروها با فشار آب منفذی N و عکسالعمل T در حالت تعادل قرار دارند.
در روش معمولی قطعات، نیروهای برآیند عمودی و افقی از طریق روابط زیر به دست میآیند:
k، یک ضریب خطی است که میزان افزایش نیروی افقی نسبت به عمق قطعه را نشان میدهد. با حل رابطه نیروی افقی نسبت به N داریم:
در مرحله بعد، فرض میشود که هر قطعه میتواند حول یک مرکز دوران کند. به علاوه، گشتاور حول این مرکز نیز باید در حالت تعادل قرار داشته باشد. رابطه تعادل گشتاورهای تمام قطعات به صورت زیر نوشته میشود:
j: شاخص قطعه؛ fi ،Rj ،xj ،ei: بازوهای گشتاور؛ بارگذاریهای سطحی در این رابطه نادیده گرفته شدهاند.
پس از جایگذاری نیروی برشی در معادله گشتاور، میتوان آن را برای تعیین نیروهای برشی در سطح لغزش استفاده کرد:
با به کارگیری تئوری ترزاقی و تبدیل تنشها به گشتاور خواهیم داشت:
uj، فشار آب منفذی را نمایش میدهد. ضریب ایمنی در این حالت، نسبت گشتاور ماکزیمم به گشتاور تخمینی خواهد بود:
روش بیشاپ اصلاح شده
«روش بیشاپ اصلاح شده» (Modified Bishop’s Method) با روش معمولی قطعات کمی متفاوت است. در روش بیشاپ اصلاح شده فرض میشود که فعل و انفعالات بین قطعات مجاور بر روی یک خط مشترک قرار دارند و برآیند نیروی برشی بین قطعات صفر است. محدودیت ناشی از نیروهای نرمال بین قطعات باعث نامعین شدن مسئله از نظر استاتیکی میشود. در نتیجه، به منظور تعیین ضریب ایمنی باید از روشهای مبتنی بر تکرار استفاده کرد. مطالعات صورت گرفته نشان میدهند که مقادیر ضریب ایمنی به دست آمده از این روش در محدوده چنددرصدی مقادیر صحیح قرار میگیرند. ضریب ایمنی تعادل گشتاور در روش بیشاپ به صورت زیر تعریف میشود:
که در آن
j: شاخص قطعه؛ ′c: چسبندگی مؤثر؛ ′ϕ: زاویه اصطکاک داخلی مؤثر؛ l: عرض هر قطعه؛ W: وزن هر قطعه؛ u: فشار آب وارده بر پایه هر قطعه
برای تعیین مقدار F باید از یک روش مبتنی بر تکرار استفاده شود زیرا ضریب ایمنی در هر دو سمت راست و چپ معادله ظاهر شده است.
روش لوریمر
«روش لوریمر» (Lorimer's Method)، رویکردی برای ارزیابی پایداری شیب در خاکهای چسبنده است. در این روش، از یک سطح لغزش منحنی شکل (کلوتوئید) در ناحیه شکست استفاده میشود. این حالت شکست به طور تجربی و برای در نظر گرفتن اثرات سمنتاسیون یا سیمانی شدن ذرهای به دست آمده است.
روش اسپنسر
تحلیل پایداری شیب با روش اسپنسر به یک برنامه کامپیوتری با قابلیت اجرای الگوریتمهای دایرهای نیاز دارد. این روش تحلیل پایداری شیب را سادهتر میکند. دقت روش اسپنسر به اندازه روش بیشاپ اصلاح شده نیست اما برای به کارگیری در مسائل مهندسی قابل قبول است.
روش سارما
روش سارما، یک رویکرد تعادل حدی برای ارزیابی پایداری شیبها در شرایط لرزهای (دینامیک) است. در صورتی که مقدار بار افقی صفر در نظر گرفته شود میتوان این روش را برای شرایط استاتیک نیز مورد استفاده قرار داد. روش سارما، امکان تحلیل طیف گستردهای از حالتهای شکست مختلف نظیر مکانیسم شکست گوهای را فراهم میکند و هندسه سطح لغزش در آن به حالتهای صفحهای یا دایرهای محدود نمیشود. در این روش میتوان اطلاعاتی در مورد ضریب ایمنی یا شتاب بحرانی مورد نیاز برای ریزش شیب را به دست آورد.
مقایسه روشهای تعادل حدی
در جدول زیر، فرضیات به کار گرفته شده در هر یک از این روشهای تعادل حدی مشاهده میکنید:
| روش | فرضیات |
| روش معمولی قطعات | نیروهای بین قطعات نادیده گرفته میشوند. |
| بیشاپ اصلاح شده/ساده شده | برآیند نیروهای بین قطعات افقی است. هیچ نیروی برشی بین قطعات وجود ندارد. |
| جانبوی ساده شده | برآیند نیروهای بین قطعات افقی است. یک ضریب اصلاح تجربی برای نیروهای برشی بین قطعات در نظر گرفته میشود. |
| جانبوی تعمیم یافته | یک خط فشار (تراست) فرضی برای تعریف محل نیروی نرمال بین قطعات تعریف میشود. |
| اسپنسر | زاویه برآیند نیروهای بین قطعات درون توده لغزشی ثابت است. |
| چاف | نیروی شتاب در هر قطعه ثابت است. |
| مورگنستون-پرایس | جهت برآیند نیروهای بین قطعات با استفاده از یک تابع اختیاری تعریف میشود. کسری از مقدار تابع برای محاسبه تعادل گشتاور و نیرو مور نیاز است. |
| فردلاند-کران | فرضیات این روش مشابه روش مورگنستون-پرایس است. |
| سپاه مهندسی | برآیند نیروی بین قطعات یا به صورت موازی با سطح زمین است یا با میانگین زاویه سطح لغزش از ابتدا تا انتهای آن برابری میکند. |
| لو-کارافیت | جهت برآیند نیروی بین قطعات با میانگین زاویه سطح زمین و پایه هر قطعه برابر است. |
| سارما | برای برش طرفین و بخش پایینی هر قطعه از معیار مقاومت برشی استفاده میشود. شیب پایه هر قطعه تا رسیدن به یک معیار بحرانی تغییر میکند. |
جدول زیر، شروط تعادل استاتیکی و وضعیت برآورده شدن آنها توسط برخی از روشهای معروف تعادل حدی را نمایش میدهد:
| روش | تعادل نیروی عمودی | تعادل نیروی افقی | تعادل گشتاور |
| معمولی قطعات | بله | خیر | بله |
| بیشاپ ساده شده | بله | خیر | بله |
| جانبوی ساده شده | بله | بله | خیر |
| جانبوی تعمیم یافته | بله | بله | برای محاسبه نیروهای برشی بین قطعات مورد استفاده قرار میگیرد. |
| اسپنسر | بله | بله | بله |
| چاف | بله | بله | بله |
| مورگنستون-پرایس | بله | بله | بله |
| فردلاند-کران | بله | بله | بله |
| سپاه مهندسی | بله | بله | خیر |
| لو-کارافیت | بله | بله | خیر |
| سارما | بله | بله | بله |
تحلیل پایداری شیبهای سنگی
تحلیل پایداری شیبهای سنگی بر اساس روشهای تعادل حدی را میتوان به حالتهای شکست زیر تقسیم کرد:
- «شکست صفحهای» (Planar Failure): در این حالت، توده سنگ بر روی یک سطح منفرد میلغزد. برای شکستهای صفحهای میتوان از یک تحلیل دوبعدی بر اساس مفهوم تعادل حدی برای یک بلوک مقاوم بر روی صفحه شیب استفاده کرد.
- «شکست چندضلعی» (Polygonal Failure): لغزش سنگهای طبیعی معمولاً بر روی سطوح چندضلعی رخ میدهد. در این حالت، محاسبات مورد نیاز بر اساس فرضیات خاصی انجام میشود. از دیدگاه سینماتیکی، لغزش بر روی یک سطح چندضلعی متشکل از N قطعه، تنها در صورت شکلگیری حداقل (N-1) سطح برشی داخلی امکانپذیر است. به این ترتیب، توده سنگ توسط سطوح برشی داخلی به چندین بلوک تقسیم میشود. این بلوکها صلب هستند و هیچ مقاومت کششی در آنها وجود ندارد.
- «شکست گوهای» (Wedge Failure): تحلیلهای سهبعدی، امکان مدلسازی لغزش گوهای بر روی دو صفحه و در امتداد خط تقاطع آنها را فراهم میکنند.
- «شکست واژگونی» (Toppling Failure): اگر به دلیل وجود ناپیوستگیهایی با شیب تند، توده سنگ به بلوکهای بلند و نازک تقسیم شود، امکان دوران هر بلوک نسبت به یک نقطه محوری (در پایینترین گوشه آن) وجود دارد. جمع گشتاورهای به وجود آورنده واژگونی یک بلوک (مؤلفه افقی وزن و جمع نیروهای محرک بلوکهای مجاور در پشت بلوک مورد نظر) با جمع گشتاورهای مقاوم در برابر واژگونی (مؤلفه عمودی وزن و جمع نیروهای مقاوم بلوکهای مجاور در جلوی بلوک مورد نظر) مقایسه میشوند. در صورتی که گشتاورهای محرک از گشتاورهای مقاوم بیشتر باشند، واژگونی رخ خواهد داد.
نرمافزارهای تحلیل تعادل حدی
در این بخش، به معرفی نرمافزارهایی میپردازیم که از روشهای تعادل حدی به عنوان مبنای تحلیل خود استفاده میکنند:
- «Slide2/Slide3»: از نرمافزارهای پرکاربرد دوبعدی و سهبعدی در زمینه محاسبه پایداری شیبهای سنگی و خاکی و عضو مجموعه نرمافزاری معروف «Rocscience» هستند. این نرمافزارها امکان بهرهگیری از روشهای تحلیل دقیق مانند اسپنسر، سارما و مورگنسترن-پرایس و همچنین روشهای غیر دقیق نظیر بیشاپ ساده شده، جانبوی ساده شده/اصلاح شده، فلنیوس و بسیاری از روشهای دیگر تعادل حدی را فراهم میکنند. جستجو برای تعیین سطح لغزش بحرانی به کمک یک شبکه یا ناحیه تعریف شده توسط کاربر صورت میگیرد. این نرمافزارها قابلیت اجرای تحلیلهای آماری به وسیله روشهای مونت کارلو یا ابرمکعب لاین را نیز دارند. در این تحلیلها میتوان هر یک از پارامترهای ورودی را به عنوان متغیر تصادفی در نظر گرفت. تحلیلهای آماری، احتمال شکست و شاخص قابلیت اطمینان شیب را به دست میآورند. این نتایج، نمایش بهتری از سطح ایمنی شیب را فراهم میکنند. تحلیلهای برگشتی نیز برای محاسبه بار نگهداری به همراه یک ضریب ایمنی مورد نیاز با مقدار مشخص به کار گرفته میشوند. این نرمافزارها، قادر به تحلیل المان حدی نشت آب زیرزمینی نیز هستند.
- «SLOPE/W»: یکی از نرمافزارهای موجود در مجموعه نرمافزاری «GeoStudio» است. این نرمافزار از روش تعادل حدی مورگنستون-پرایس، اسپنسر، بیشاپ، جانبو و غیره برای تحلیل پایداری شیب استفاده میکند. SLOPE/W، بر مبنای معادلات ضریب ایمنی برای تعادل گشتاور و نیرو توسعه یافته است. امکان ادغام این برنامه با دیگر برنامههای موجود در مجموعه نرمافزاری GeoStudio وجود دارد. به عنوان مثال، با استفاده از تنشهای به دست آمده از «SIGMA/W» یا «QUAKE/W» و تعیین مقاومت برشی کل و تنش برشی محرک در سراسر سطح لغزش میتوان ضریب پایداری شیب را محاسبه کرد. پس از این کار، یک ضریب پایداری موضعی برای هر قطعه به دست میآید. یکی دیگر از قابلیتهای SLOPE/W، محاسبه احتمال شکست با به کارگیری رویکرد مونت کارلو است.
- «STABL WV»: یک نرمافزار تحلیل پایداری شیب مبتنی بر روش تعادل حدی و بخشی از مجموعه نرمافزاری «STABL» است. این نرمافزار تنها بر روی سیستم عامل ویندوز اجرا میشود. STABL WV، از روشهای بیشاپ، اسپنسر و جانبو استفاده میکند. تحلیل شیبهای معمولی و همچنین شیبهایی با ویژگیهای مختلف در این نرمافزار امکانپذیر است.
- «HYDRUS»: برنامهای با قابلیت ارزیابی پایداری خاکریزها، سدها، گودبرداریها و شیبهای نگهداری شده است. این برنامه به صورت ماژولار بوده و امکان اضافه کردن و به کارگیری افزونههای مختلف را دارد. به علاوه، در این برنامه میتوان از روش قطعات (بیشاپ، مورگنستون-پرایس، اسپنسر یا فلنیوس) و همچنین انواع مختلف نگهدارنده یا اثرات زلزله استفاده کرد.
- «SVSlope»: یک برنامه تحلیل پایداری شیب و بخشی از مجموعه نرمافزاری «SoilVision» است. این برنامه از روشهای تعادل حدی مورگنستون-پرایس، اسپنسر، بیشاپ و غیره استفاده میکند. SVSlope، قابلیت ادغام با دیگر نرمافزارهای ژئوتکنیکی مجموعه SoilVision را دارد. به عنوان مثال، تنشهای محاسبه شده از طریق برنامه «SVSolid» یا فشارهای آب منفذی به دست آمده از برنامه «SVFlux» را میتوان برای محاسبه ضریب ایمنی از طریق تعیین مقاومت برشی کل و تنش برشی محرک در امتداد سراسر سطح لغزش مورد استفاده قرار داد. به علاوه، SVSlope از قابلیت به کارگیری رویکردهای آماری مونت کارلو، ابرمکعب لاتین و APEM نیز بهره میبرد.
- «dotSlope»: این برنامه، امکان تحلیلهای تعادل حدی با به کارگیری روشهای فلنیوس، بیشاپ ساده شده، جانبوی ساده شده/اصلاح شده، سپاه مهندسی، لو-کارافیت، اسپنیر و مورگنستون-پرایس را فراهم میکند. با استفاده از این برنامه میتوان انواع مختلف خاکها، لایههای غیر قابل نفوذ، گودبرداری و خاکریزها، شرایط مختلف آب زیرزمینی، آب راکد، ترکهای کششی خشک یا مرطوب و نگهداریهای خاکی از قبیل کابلهای مهاری، میخکوبیها و شمعها را در نظر گرفت. سطوح لغزش بحرانی شیب نیز با کمک شش تولیدکننده سطح تعریف میشود. از دیگر قابلیت dotSlope میتوان به اجرای تحلیلهای قطعی، بهینهسازی سطح و تحلیل حساسیت به همراه تحلیلهای آماری با استفاده از روش مونت کارلو اشاره کرد.
- «GALENA»: این برنامه امکان اجرای تحلیلهای پایداری، برگشتی و آماری با استفاده از روشهای بیشاپ، اسپنسر-رایت و سارما را فراهم میکند.
- «GSLOPE»: در این برنامه، از روشهای تعادل حدی بیشاپ اصلاح شده و جانبوی ساده شده برای تحلیل شیبهای طبیعی، شیبهای بدون نگهداری یا شیبهای داری نگهداری خاکی استفاده میشود. سطح لغزش در روشهای مذکور به صورت دایرهای، ترکیبی یا غیر دایرهای است.
- «CLARA-W»: یک برنامه تحلیل پایداری شیبهای سهبعدی است که برای انجام محاسبات خود از روشهای بیشاپ ساده شده، جانبوی ساده شده، اسپنسر و مورگنستون-پرایس استفاده میکند. پیکربندی مسئله در این برنامه به سطح لغزش دورانی یا غیر دورانی، بیضوی، گوه، سطح ترکیبی، سطح کاملاً مشخص و جستجوی سطح لغزش تقسیم میشود.
- «TSLOPE3»: این برنامه برای تحلیلهای دوبعدی و سهبعدی شیبهای خاکی و سنگی با استفاده از روش اسپنسر به کار میرود.
- «AutoBlock»: برنامهای مخصوص برای تحلیل شیبهای سنگی است. این برنامه، دو مشکل ذاتی که باعث پیچیده شدن تحلیل پایداری شیب میشود را رفع میکند. در ابتدا، مقدار حجم و مساحت نواحی لغزشی بلوکهای احتمالاً ناپایدار با استفاده از توپوگرافی واقعی تعیین میشود. در مرحله بعد، جستجوی بلوکهای بحرانی متشکل از تقاطع ناپیوستگیهای مختلف صورت میگیرد. در این برنامه، علاوه بر به کارگیری نقشههای توپوگرافی، امکان اضافه کردن سطوح پیچیده زمین به صورت دلخواه نیز وجود دارد. سطوح وارد شده را میتوان به اجسام سهبعدی تبدیل کرد. ناپیوستگیهای موجود با این سطوح تقاطع پیدا میکنند و با ترکیب محل قرارگیری احتمالی تمام ناپیوستگیها، بلوکهای مستعد لغزش مشخص میشوند. در ادامه، ضریب ایمنی هر بلوک در برابر لغزش با استفاده از روش تعادل حدی به دست میآید. AutoBlock، افزونهای است که در نرمافزار شناخته شده AutoCAD مورد استفاده قرار میگیرد. این موضوع، قابلیتهای AutoBlock در نمایش سهبعدی مسائل را افزایش میدهد.












