تقارن چرخشی در اشکال دوبعدی — به زبان ساده

در این آموزش، در خصوص تقارن چرخشی در اشکال دو بعدی صحبت خواهیم کرد.

اشکالی که پس از چرخش یه اندازه مشخصی، همچنان بدون تغییر باقی بمانند دارای تقارن چرخشی هستند.

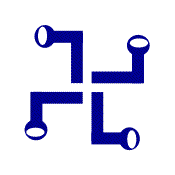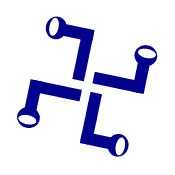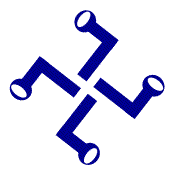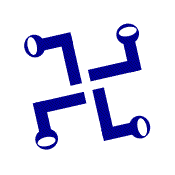
تعداد دفعاتی که شکل موردنظر با یک بار چرخش کامل (360درجه) بر شکل اولیه منطبق می شود را مرتبه می نامند. برای مثال تقارن در شکل بالا، از مرتبه 4 است.

مثال‌هایی از تقارن چرخشی با مرتبه‌های متفاوت

مرتبه	شکل نمونه	طرح نمونه
. . .	. . .	. . .
. . .	. . .	. . .

آیا تقارن چرخشی از مرتبه 1 نیز وجود دارد؟

این مرتبه از تقارن چرخشی بدین معناست که هندسه مان با یکبار چرخش کامل، تنها یک دفعه بر شکل اولیه منطبق شود. اما در این صورت دیگر شکل هندسی ما تقارنی ندارد که بخواهیم برای آن مرتبه تعیین نماییم. پس می‌توان گفت هندسه‌ای با تقارن چرخشی از مرتبه 1 وجود ندارد.

نمونه‌هایی از تقارن چرخشی در دنیای واقعی

اگر تمایل به مطالعه بیشتر در این موضوع داشته باشید، شاید آموزش های زیر نیز برای شما مفید باشند:

• آشنایی با تبدیلات هندسی
• تقارن محوری در اشکال دوبعدی
• آموزش جامع هندسه تحلیلی
• آموزش ریاضی پایه
• آموزش ریاضیات عمومی

**

منبع