قضیه فیثاغورس و کاربردهای آن – به زبان ساده
قضیه فیثاغورس (فیثاغورث نیز نوشته میشود) بسیار مشهور است و احتمالاً تاکنون در جاهای مختلفی با آن مواجه شدهاید. اما اغلب ما تصور میکنیم این فرمول تنها در مورد مثلثها و هندسه به کار میرود. در این صورت باید در طرز فکر خود تجدید نظر کنید. قضیه فیثاغورس میتواند در مورد هر نوع شکلی برای هر فرمولی که در آن مربع یک عدد استفاده میشود به کار گرفته شود.

در ادامه این نوشته توضیح دادهایم که چگونه این ایده 2500 ساله میتواند به درک ما از علوم کامپیوتر، فیزیک و حتی ارزش شبکههای اجتماعی وب 2.0 کمک کند.
درکی جدید از مساحت
نکاه کردن به مسائل قدیمی به روشی جدید و کشف ژرفای جدید همواره کاری لذتبخش محسوب میشود. برای نمونه ممکن است پس از خواندن این مقاله طرز فکر شما در مورد مساحت به کلی تغییر یابد. البته ممکن است فکر کنید همه معادلات مربوط به مساحت را میدانید، اما آیا ماهیت واقعی این مفهوم را متوجه شدهاید؟ این واقعیت میتواند شما را شگفتزده کند.
مساحت هر شکلی را میتوان با مربع کردن یک پارهخط آن به دست آورد. در یک مربع «پارهخط» معمولاً یک ضلع آن مربع محسوب میشود و مساحت نیز در واقع مربع آن ضلع (ضلع 5 و مساحت 25) است. در یک دایره آن پارهخط غالباً شعاع است و مساحت π r² (شعاع 5، مساحت 25 π) است. در واقع محاسبه بسیار سادهای است.
ما میتوانیم هر پارهخطی را انتخاب کنیم و مساحت را بر اساس آن محاسبه کنیم. در این معادله سراسری، هر پارهخط یک «ضریب مساحت» دارد:
2(پاره خط) × عامل = مساحت
| شکل | پاره خط | مساحت | عامل مساحت |
|---|---|---|---|
مربع | ضلع [s] | s2 | 1 |
مربع | محیط [p] | 1/16 p2 | 1/16 |
مربع | قطر [d] | 1/2 d2 | 1/2 |
دایره | شعاع [r] | π r2 | π (3.14159...) |
برای نمونه به قطر مربع (d) نگاه کنید. یک ضلع به صورت d/√2 است و از این رو مساحت باید d2 1/2 باشد. اگر بخواهیم از قطر به عنوان پارهخطی برای محاسبه مساحت استفاده کنیم، ثابت مساحت ما در این جا 1/2 است.
اینک از محیط کلی (p) به عنوان پارهخط استفاده میکنیم. یک ضلع برابر با p/4 است و از این رو مساحت برابر است با p2/16. اگر بخواهیم از p2 استفاده کنیم، عامل مساحت در این جا 1/16 خواهد بود.
آیا میتوان هر پارهخطی را انتخاب کرد؟
ممکن است فکر کنید همواره نوعی رابطه بین پارهخط «معمول» برای محاسبه مساحت (ضلع مربع) و پارهخطی که ما انتخاب میکنیم (محیط، که 4 برابر ضلع است) وجود دارد. از آنجا که میتوانیم بین این پارهخط جدید و پارهخط سنتی تبدیل انجام دهیم مهم نیست که از کدام برای محاسبه مساحت استفاده کنیم و در زمان محاسبه تنها یک عامل متفاوت ظاهر خواهد شد.
آیا میتوان هر شکلی را انتخاب کرد؟
شاید چنین باشد. یک فرمول مساحت معین برای همه شکلهای مشابه پاسخگو است و منظور ما از مشابه، نسخههای بزرگنمایی شده از شکلها است. برای نمونه:
- همه مربعها مشابه هم هستند (مساحت همیشه ضلع به توان 2 است).
- همه دایرهها نیز مشابه هستند (مساحت همواره توان 2 شعاع در عدد پی است)
- مثلثها مشابه نیستند. برخی از آنها عریض و برخی کشیده هستند. هر نوع از مثلث عامل مساحت خاص خود را بر مبنای پارهخطی که استفاده میکنیم دارد. با تغییر شکل مثلث، معادله نیز تغییر مییابد.
در مورد هر مثلثی میتوان گفت: «مساحت = ½ * قاعده»؛ اما رابطه بین قاعده و ارتفاع به نوع مثلث بستگی دارد. در برخی مثلثها قاعده = دو برابر ارتفاع است و در برخی دیگر قاعده = 3 برابر ارتفاع است. بنابراین حتی در این مورد نیز عامل مساحت متفاوت خواهد بود.
ما چرا برای حفظ معادله مساحت به شکلهای یکسان نیاز داریم؟ به طور شهودی وقتی روی یک شکل زوم میکنید، اندازه مطلق تغییر مییابد؛ اما اندازه نسبی بین اجزا تغییر نمییابد. یک مربع صرفنظر از این که چه مقدار بزرگنمایی شده باشد، محیطی برابر با 4 برابر طول یک ضلع دارد.

از آنجا که عامل مساحت بر مبنای نسبتهای درون شکل است، هر شکلی که همان نسبتها را داشته باشد از همین فرمول پیروی میکند. مانند این است که بگوییم طول فاصله بین دو بازوی هر فرد، تقریباً برابر با قد اوست. مهم نیست که شما یک بازیکن بسکتبال باشید یا یک کودک خردسال؛ چون در هر صورت این اندازه نسبی صحیح است. البته این استدلال شهودی ممکن است یک ذهن ریاضی را قانع نسازد.
مواردی که در این بخش مطرح شد را به صورت زیر میتوان جمعبندی کرد:
- مساحت را میتوان از مربع هر خطی در شکل محاسبه کرد و لازم نیست صرفاً از ضلع یا شعاع استفاده کنیم.
- هر پارهخط «عامل مساحت» متفاوتی دارد.
- در مورد شکلهای مشابه میتوان از معادله مساحت یکسانی استفاده کرد.
نگاهی شهودی به قضیه فیثاغورث
با وجود صدها اثباتی که برای قضیه فیثاغورس ارائه شده است، میتوان در مورد صحت آن کاملاً مطمئن بود. اما اغلب این اثباتها از یک درک مکانیکی استفاده میکنند. کافی است شکلهایی را بازآرایی کنید و ناگهان ثابت میشود که معادله صحیح است. اما آیا از نظر شهودی نیز این استدلال صحیح است. یعنی آیا میتوان تصور کرد که همواره a2 + b2 = c2 است و هیچ گاه 2a2 + b2 = c2 نیست؟ در ادامه تلاش میکنیم، درکی شهودی ارائه دهیم. در ابتدا یک مفهوم بنیادی وجود دارد که باید بررسی کنیم:
هر مثلث قائمالزاویه را میتوان به دو مثلث قائمالزاویه مشابه افراز کرد.
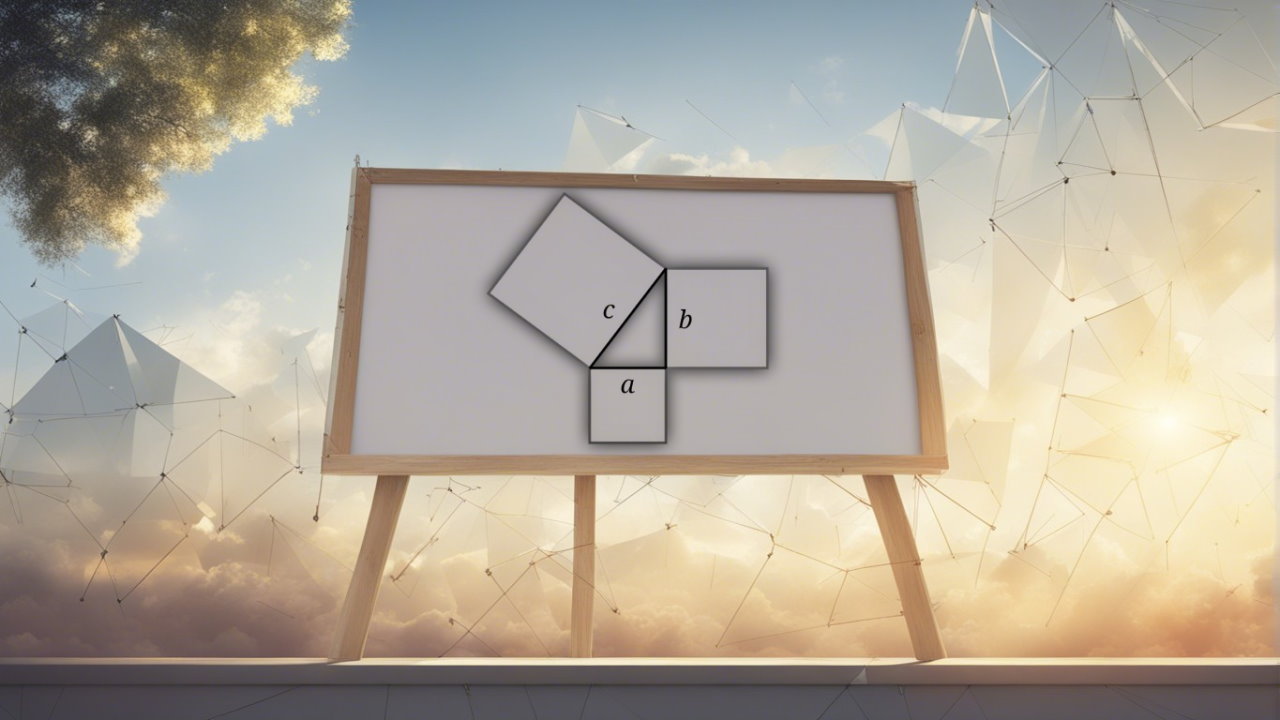
ترسیم یک خط قائم بر قاعده مثلث به طوری که از نوک آن بگذرد باعث میشود که دو مثلث قائمالزاویه مشابه به دست آوریم. عاشقان هندسه میتوانند این اثبات را خودشان امتحان کنند. بدین منظور میتوانید از مشابهت زاویه-زاویه-زاویه استفاده کنید. تصویر فوق یک نکته را نیز کاملاً مشخص میسازد:
مساحت (مثلث بزرگ) = مساحت (مثلث متوسط) + مساحت (مثلث کوچک)
مثلثهای کوچکتر از مثلث بزرگ بریده شدهاند و از این رو مجموع آنها باید با مساحت مثلث بزرگ برابر باشد. از آنجا که مثلثها مشابه هستند، معادله مساحت آنها نیز یکسان است.
فرض کنید ضلع بزرگتر (5) را c بنامیم، همچنین ضلع متوسط (4)، b و ضلع کوچک (3) a نام دارد. معادله مساحت برای این مثلث به صورت زیر خواهد بود:
2وتر × F = مساحت
که F نوعی عامل مساحت است. در این مثال این عامل برابر با 6/25 یا 0.24 است که البته عدد دقیق اهمتی ندارد. اینک کمی این معادله را بررسی میکنیم:
مساحت (مثلث بزرگ) = مساحت (مثلث متوسط) + مساحت (مثلث کوچک)
Fc2 = Fb2 + Fa2
اگر معادله فوق را بر F تقسیم کنیم، معادله زیر را به دست میآوریم:
c2 = b2 + a2
که همان قضیه مشهور ما است. اینک دانستیم که این قضیه صحیح است؛ اما دلیل آن را در ادامه توضیح میدهیم:
- یک مثلث میتواند به دو مثلث کوچکتر مشابه افراز شود
- از آنجا که مساحتها باید با هم جمع شوند، مربع وتر (که مساحت را تعیین میکند) نیز باید جمع شود
گرچه نشان دادن این واقعیت اندکی زمان بُرد؛ اما در نهایت کاملاً گویا است. اگر مثلثهای کوچک به مثلث بزرگ اضافه نشوند چه رخ میدهد؟
در واقع مشخص شده است که قضیه فیثاغورس به فرضیات هندسه اقلیدسی وابسته است و بر روی کره مصداق ندارد.
کاربردهای مفید: کاربرد قضیه فیثاغورس در مورد هر شکل
ما از مثلث در نمودار خود به عنوان سادهترین شکل 2 بعدی استفاده کردیم. اما این پارهخط میتواند به هر شکلی تعلق داشته باشد. برای نمونه دایره را در نظر بگیرید:
اینک وقتی آنها را با هم جمع کنیم چه اتفاقی میافتد؟
مسلماً میتوانید حدس بزنید. مساحت دایره با شعاع 5 برابر با مساحت دایره با شعاع 4 و دایره با شعاع 3 است.
میتوانیم قضیه فیثاغورس را در عامل مساحت که در این مورد عدد π است ضرب کنیم و برای این کل نیز به رابطهای مشابه دست یابیم. به خاطر داشته باشید که پارهخط میتواند هر بخشی از شکل باشد. ما میتوانیم شعاع، قطر یا محیط دایره را نیز انتخاب کنیم. در هر صورت عامل مساحت متفاوت خواهد بود؛ اما رابطه 3-4-5 همواره صحیح است.
بنابراین چه بخواهید پیتزاها را جمع بزنید یا هر چیز دیگری را با هم جمع کنید در هر صورت رابطه فیثاغورس صدق میکند و رابطه بین مساحت شکلهای مشابه را نشان میدهد. در ادامه نکتهای را به شما خواهیم گفت که در دبستان یا دبیرستان نیاموختهاید.
کاربردهای مفید: حفظ مربعها
قضیه فیثاغورس در مورد هر معادلهای که یک توان 2 در آن هست صدق میکند. افراز مثلثی به معنی این است که هر مقداری (مانند c2) را به دو مقدار کوچکتر (a2 + b2) بر اساس اضلاع مثلث افراز کنیم. در واقعیت «طول» یک ضلع میتواند مسافت، انرژی، کار، زمان یا حتی افرادی باشد که در یک شبکه اجتماعی حضور دارند:
شبکههای اجتماعی
بر اساس قانون متکالیف (Metcalfe) ارزش یک شبکه در حدود n² است که n تعداد روابط است. برحسب ارزش
شبکه 50 میلیونی = شبکه 40 میلیونی + شبکه 30 میلیونی
کاملاً شگفتانگیز است! شبکههای دوم و سوم مجموعاً 70 میلیون عضو دارند؛ اما هنوز ادغام نشدهاند. شبکهای با 50 میلیون عضو ارزشی به اندازه دو شبکه دیگر دارد.
علوم رایانه
برخی برنامهها با n ورودی برای اجرا به n² زمان برای اجرا نیاز دارند (برای مثال مرتبسازی حبابی چنین است) برحسب زمان مورد نیاز برای پردازش:
50 ورودی = 40 ورودی + 30 ورودی
در این مورد نیز در نهایت شگفتی میبینیم که 70 عضو که در میان دو گروه تقسیم شده باشند میتوانند با سرعتی برابر با 50 عضو در یک گروه مرتبسازی شوند. البته ممکن است برخی هزینههای سربار مانند زمان آغاز به کار و غیره وجود داشته باشند، ولی ماهیت مفهوم همین است.
با توجه به این رابطه معقول است که عناصر را ابتدا به زیرگروههایی تقسیم کرد و سپس آنها را مرتبسازی نمود. در واقع این همان رویکردی است که در روش مرتبسازی quicksort استفاده میشود و یکی از بهترین روشهای مرتبسازی چندمنظوره است. قضیه فیثاغورس به ما کمک میکند دریابیم چرا مرتبسازی 50 عنصر به صورت ترکیب با هم میتوانند به اندازه 30 و 40 عنصر جدا از هم، هزینه داشته باشند.

مساحت سطحی
مساحت سطحی کره برابر با 4π r² است. بنابراین برحسب مساحت سطحی کره:
مساحت شعاع 50 = مساحت شعاع 40 + مساحت شعاع 30
شاید فکر کنید که در زندگی روزمره چندان از کره استفاده نمیکنیم تا در این مورد مثالی بزنیم. اما قایقها هم شاید شکلی شبیه نوعی کره داشته باشند. با فرض این که قایقها کاملاً شبیه هم باشند، برای نقاشی بدنه قایقی که 50 متر طول دارد، میتوانید از مقدار رنگی که برای رنگآمیزی قایقهای 30 و 40 متری کافی است استفاده کنید!
فیزیک
اگر از کلاسهای فیزیک خود به خاطر داشته باشید، انرژی جنبشی یک شیء با جرم m و سرعت v برابر با mv2 1/2 خواهد بود. برحسب انرژی:
انرژی در سرعت 500 کیلومتر بر ساعت = انرژی در سرعت 400 کیلومتر بر ساعت + انرژی در 300 کیلومتر بر ساعت
در واقع با انرژی مورد نیاز برای شتاب گیری یک گلوله تا 500 کیلومتر بر ساعت میتوانیم دو گلوله را به ترتیب به سرعتهای 400 و 300 کیلومتر بر ساعت برسانیم.
به عنوان یک مثال دیگر میتوان گفت که اگر یک پیتزای بزرگ (40 سانتیمتری) بزرگتر از دو عدد پیتزای متوسط (30 سانتیمتری) باشد، در این صورت میتوان بر اساس رابطه فیثاغورس میبینیم که پیتزای بزرگتر میتواند برابر با دو پیتزا به قطر یکی 30 و دیگری 26.24 باشد. بنابراین در عمل دو پیتزای متوسط از یک پیتزای بزرگ، بزرگتر هستند.
سخن پایانی
همه ما در تمام طول دوران تحصیل فکر میکردیم که قضیه فیثاغورس به مثلثها و هندسه مربوط است؛ اما دیدیم که چنین نیست.
زمانی که یک مثلث قائمالزاویه را میبینید، درمی یابید که اضلاع میتوانند طول هر بخش از یک شکل را نشان دهند. همچنین ضلعها میتوانند متغیرهایی که در هر معادلهای که توان 2 دارد را توصیف کنند. این واقعت کاملاً شگفتانگیز است.
آزمون قضیه فیثاغورس
۱. قضیه فیثاغورس چگونه ارتباط میان مربع هر پارهخط و مساحت را فراتر از مثلث قائمالزاویه توصیف میکند؟
هر پارهخط دلخواه با ضریب مناسبش میتواند برای یافتن مساحت به کار رود.
برای هر شکل تنها از ضلع اصلی جهت محاسبه مساحت استفاده میشود.
مربع بودن پارهخطها صرفا محدود به هندسه اقلیدسی است.
این قضیه فقط برای محاسبه مساحت مثلثها با زاویه قائمه کاربرد دارد.
بر اساس توضیحات، اگر ضریب یا عامل مناسب را در نظر بگیریم، هر پارهخط دلخواه مثل قطر یا محیط (و در دایره، شعاع) را میتوان برای بیان مساحت هر شکل مشابه به کار برد. محدودیتی در انتخاب پارهخط وجود ندارد و تنها لازم است عامل مساحت مرتبط با آن تنظیم شود.
۲. در محاسبه مساحت یک مربع اگر بهجای ضلع از پارهخطی مثل قطر یا محیط استفاده کنیم، عامل مساحت (ضریب) چه تاثیری دارد و چرا نوع پارهخط انتخابی اهمیت زیادی پیدا نمیکند؟
انتخاب نوع پارهخط باعث میشود فرمول مساحت غیرقابل استفاده شود و فقط ضلع درست عمل میکند.
با تغییر پارهخط، کافی است عامل مساحت (ضریب) را اصلاح کنیم و نوع پارهخط تاثیری در امکان محاسبه ندارد.
برای هر پارهخط باید فرمول کاملا متفاوتی ساخت و عامل مساحت بیاهمیت است.
عامل مساحت فقط هنگام استفاده از ضلع کاربرد دارد و برای قطر یا محیط نتیجه اشتباه میشود.
هنگامی که برای محاسبه مساحت مربع به جای ضلع از پارهخطهای دیگری مانند قطر یا محیط استفاده شود، کافی است ضریب یا عامل مساحت را متناسب با رابطه آن پارهخط با ضلع اصلاح کنیم؛ بنابراین نوع پارهخط مانند «قطر» یا «محیط» در اصل فرمول محدودیتی ایجاد نمیکند و کافی است ضریب مناسب انتخاب شود.
۳. برای اینکه مساحت یک دایره را بر اساس شعاع و مساحت یک مربع را با استفاده از قطر محاسبه کنیم، چه تغییری باید در عامل مساحت هرکدام ایجاد شود تا فرمول نتیجه درست بدهد؟
عامل مساحت دایره را برابر π گذاشته و برای مربع از ۱ استفاده کنیم.
عامل مساحت دایره را π و در مربع برای قطر مقدار ۱/۴ انتخاب کنیم.
برای دایره عامل مساحت را ۲π و برای مربع ۲ انتخاب کنیم.
در دایره عامل مساحت π و در مربع مقدار ۱/۲ را برای قطر لحاظ کنیم.
برای دایره، طبق معمول عامل مساحت π است زمانی که از شعاع استفاده میشود. اما اگر بخواهیم مساحت مربع را با قطر بدست آوریم، باید به جای مقدار عادی ۱، ضریب ۱/۴ را به کار ببریم، زیرا مربع قطر از ضلع دو برابر بیشتر است و مساحت با توان دو نسبت به ضلع تغییر میکند. استفاده از مقدار ۱/۴ برای قطر، نتیجه درست را میدهد، اما عاملهایی مثل ۱/۲ یا ۲ صحیح نیستند و عدد ۱ فقط برای ضلع معتبر است.
۴. در محاسبه مساحت اشکال هندسی با استفاده از مربع یک پارهخط، چرا باید به مشابهت توجه کنیم و اثر آن بر فرمول مساحت چیست؟
فرمول مساحت همواره بدون توجه به شکل و نسبتها یکسان باقی میماند و مشابهت ضرورتی ندارد.
استفاده از پارهخط دلخواه فقط در اشکال متساویالساقین جواب میدهد و مشابهت تاثیری ندارد.
مشابهت باعث ثابت ماندن نسبتها میشود و امکان استفاده از فرمول مساحت برای هر اندازه پارهخط را فراهم میکند.
زیرا تنها اشکال با اضلاع برابر این فرمول را حفظ میکنند و در بقیه موارد نیاز به اصلاح نیست.
اگر با مشابهت در هندسه آشنا باشیم، میدانیم که نسبت درست میان اجزای شکل تنها زمانی حفظ میشود که اشکال مشابه باشند. این ویژگی باعث میشود که هنگام محاسبه مساحت با مربع پارهخط دلخواه (چه قطر و چه ضلع یا محیط)، عامل مساحت بتواند فرمول صحیح را برای هر اندازهای از شکل حفظ کند. اگر مشابهت رعایت نشود، نسبتها به هم میریزد و مساحت با مربع پارهخط ارتباط واقعی نخواهد داشت.
۵. کدام ویژگی مشترک میان پدیدههایی مانند انرژی جنبشی و زمان اجرای الگوریتم باعث میشود بتوان الگوی فیثاغورس را برای تحلیل آنها به کار برد؟
وجود مفاهیم مساحت و محیط در هر مثال
لزوم تشابه میان فرم کلی سیستمها
استفاده از نسبتهای درونی اشکال مختلف
مربعی بودن کمیت کلیدی در رابطه مورد بررسی
پدیدههایی مثل انرژی جنبشی و زمان اجرای الگوریتم را میتوان با الگوی فیثاغورس تحلیل کرد چون کمیت اصلی در این روابط به صورت مربع ظاهر میشود، یعنی فرمول پایه آنها وابسته به توان ۲ است. «مربعی بودن کمیت کلیدی در رابطه مورد بررسی» همین ویژگی را بهدرستی بیان میکند.

















سلام،
یکی دو سوال سهل و ممتنع دارم که شاید کودکانه باشند:
الف- اگر یک مثلث قائم الزاویه را روی یک توپ پینگ پنگ ( تنیس رو میزی ) رسم نمائیم و آنگاه مساحت آنرا محاسبه کنیم، بازهم قضیه پیتاگوراس ( پَی تا گو راس ) یا فیثاغورس مترجمین عرب زبان دوران عباسیان، بازهم دست نخورده باقی خواهد ماند ؟
ب – ضریب تناسب اصل هم ارزی جرم و انرژی از دیدگاه انشتاین مساوی با سرعت نور بتوان ۲ میباشد که روی سطح یک مربع حقیقت دارد، حال سوال اینست که این ضریب تناسب در درون یک کره یا مکعب مربع هم صدق میکند یا اینکه مساوی خواهد بود با حاصلضرب چهار سوم در عدد پی در c بتوان ۳؟
امیدوارم که استاد بزرگوار و شریف و ارجمند مرا بابت طرح چنین سوالاتی به بزرگواری خویش ببخشایند.
با سلام خدمت شما؛
در مورد سوال اول روی کره (مانند توپ پینگپنگ) هندسه اقلیدسی صادق نیست. پس قضیه فیثاغورس برقرار نمیماند. همچنین در سوال دوم نیز باید بدانیم رابطه همارزی جرم و انرژی یک اصل محلی و مستقل از شکل فضا (مربع، مکعب، کره و …) است و ضریب تناسب آن همیشه c2 است.
از همراهی شما با مجله فرادرس سپاسگزاریم.
واقعا فوق العاده بود دمت گرم پروفسور .
اصلا هنگ کردم .
من کامل نفهمیدم ولی ممنون همینقدر که برای تحقیق لازم داشتم فهمیدم
ممنون میشم به زبانی ساده در حد بچه متوسطه بنویسین
سلام ببخشید اگر جای وتر اندازه یکی از زاویه ها رو خواستن چه کار باید کرد؟
اگر در مثلث قائم الزاویه ضلع ها معلوم و زاویه ها مجهول باشد خیلی ساده از روابط مثلثاتی برای بدست آوردن زاویه ها استفاده می کنیم .
اندازه ضلع یا زاویه؟:|