برنامه محاسبه مثلث خیام پاسکال – راهنمای کاربردی

مثلث خیام پاسکال، آرایه مثلثی از ضرایب بسط دوجمله‌ای است. به این مثلث، «مثلث خیام»، «مثلث-پاسکال»، «مثلث خیام-پاسکال-نیوتن»، «مثلث تارتالیا» (در زبان ایتالیایی) و «مثلث یانگ هویی» (در زبان چینی) نیز گفته می‌شود. دلیل وجود نام‌های متعدد برای این مثلث آن است که دانشمندان گوناگون از نقاط مختلف جهان، شامل ایران، فرانسه، ایتالیا، چین، هند و آلمان، در برهه‌های مختلفی از تاریخ، مطالعاتی پیرامون این مثلث داشته‌اند. در این مطلب، به روش ساخت برنامه محاسبه مثلث خیام و همچنین، چگونگی پیاده‌سازی آن در زبان‌های برنامه‌نویسی گوناگون شامل ++C، «جاوا» (Java)، «پایتون» (Python)، «سی‌شارپ» (#C) و «پی‌اچ‌پی» (PHP) پرداخته شده است. سطرهای مثلث پاسکال معمولا با آغاز از بالاترین سطر، به عنوان سطر شماره صفر (یعنی n = ۰) شمارش می‌شوند. ورودی‌های هر سطر، از سمت چپ با آغاز از k = 0 شمارش می‌شوند و مقدار آن‌ها وابسته به اعداد موجود در سطرهای مجاور است. یک مثلث خیام پاسکال را می‌توان به صورت زیر ساخت.

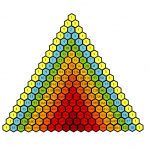
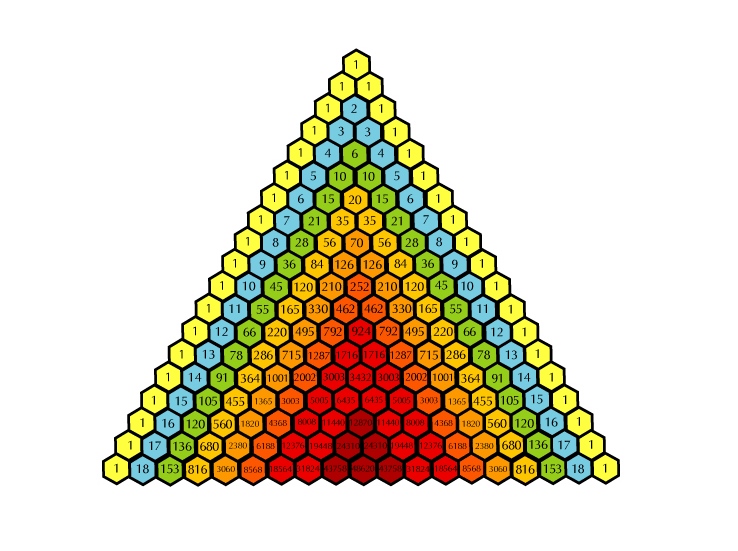
در سطر صفر (بالاترین سطر)، یک ورودی یکتای غیر صفر یعنی یک (۱) وجود دارد. هر ورودی در سطرهای زیرین، با محاسبه مجموع عددهای بالایی از چپ به راست محاسبه می‌شود و موارد فاقد ورودی، صفر محسوب می‌شوند. برای مثال، مقدار اولیه در سطر اول (یا هر سطر دیگری) برابر با یک (۱) است (جاصل جمع صفر و یک). این در حالی است که به عنوان نمونه، در سطر سوم (n = 3)، یک و سه با یکدیگر جمع می‌شوند و مقدار ۴ را برای سطر بعدی (سطر چهارم) می‌سازند. در انیمیشن زیر، آنچه بیان شد را می‌توان مشاهده کرد.

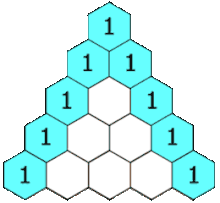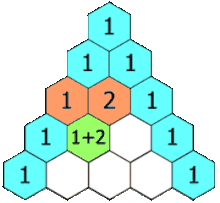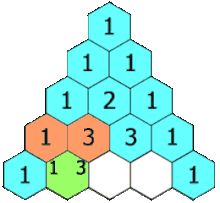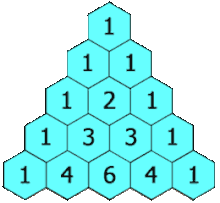
فرمول مثلث خیام پاسکال

ورودی سطر nاُم و ستون kاُم به صورت $$\left(\begin{array}{c}n\\ k\end{array}\right)$$ مشخص می‌شود. برای مثال، ورودی یکتای غیر صفر بالاترین سطر (سطر صفر و ستون صفر)، به صورت $$\left(\begin{array}{c}0\\ 0\end{array}\right)=1$$ است. با توجه به این موضوع، می‌توان روش محاسبه بیان شده در پاراگراف پیشین را به صورت زیر نوشت:

$$\left(\begin{array}{c}n\\ k\end{array}\right)=\left(\begin{array}{c}n - 1\\ k - 1\end{array}\right)+\left(\begin{array}{c}n - 1\\ k\end{array}\right)$$

برای عدد صحیح غیر صفر n و عدد صحیح k بین ۰ تا n، رابطه بازگشتی بالا برای ضرایب چندجمله‌ای برقرار است. به این فرمول، اتحاد پاسکال گفته می‌شود. اتحاد پاسال دارای تعمیم برای ابعاد بالاتر است. نسخه سه‌بُعدی مثلث خیام پاسکال را «هرم پاسکال» (Pascal's Pyramid) یا «چهار وجهی پاسکال» (Pascal's Tetrahedron) می‌نامند. نسخه تعمیم یافته را نیز «ساده پاسکال» (Pascal's Simplices) می‌نامند.

برنامه محاسبه مثلث خیام پاسکال

مثلث پاسکال یک آرایه مثلثی از ضرایب چندجمله‌ای است. هدف نوشتن تابعی است که یک مقدار صحیح n را به عنوان ورودی دریافت و اولین n سطر مثلث پاسکال را چاپ کند. در ادامه، ۶ سطر اول مثلث پاسکال نمایش داده شده‌اند.

1 
1 1 
1 2 1 
1 3 3 1 
1 4 6 4 1 
1 5 10 10 5 1

روش اول با پیچیدگی زمانی از مرتبه (O(n³

با فرض آنکه سطرها از یک شروع می‌شوند (n = 1)، تعداد ورودی‌ها در هر سطر برابر با شماره آن سطر است. برای مثال، اولین سطر دارای یک ورودی (۱) است؛ دومین سطر دو ورودی (1 1) و سومین سطر سه ورودی (1 2 1) دارد و همین قاعده برای سایر سطرها نیز صادق است. هر ورودی در یک سطر، مقدار ضریب دو جمله‌ای (در بسط دو جمله‌ای) است. مقدار iاُمین ورودی در سطر شماره line، برابر با (C(line, i است. مقدار را می‌توان با استفاده از فرمول زیر محاسبه کرد.

$$C(line, i) = line! / ( (line-i)!) * i! )$$

یک راهکار ساده، اجرای دو حلقه و محاسبه مقدار ضریب چندجمله‌ای در حلقه داخلی است.

محاسبه مثلث خیام پاسکال در ++C

محاسبه مثلث خیام پاسکال در جاوا

محاسبه مثلث خیام پاسکال در پایتون

محاسبه مثلث خیام پاسکال در #C

محاسبه مثلث خیام پاسکال در PHP

خروجی

خروجی قطعه کدهای بالا برای n = 5 به صورت زیر است.

1 
1 1 
1 2 1 
1 3 3 1 
1 4 6 4 1 
1 5 10 10 5 1 
1 6 15 20 15 6 1

پیچیدگی زمانی این روش، برابر با (O(n³ است. در ادامه، روش‌های بهینه شده نیز معرفی شده‌اند.

روش ۲ با پیچیدگی زمانی از مرتبه (O(n² و فضای اضافی (O(n²

با نگاهی دقیق‌تر به مثلث خیام، می‌توان مشاهده کرد که هر ورودی، مجموع دو مقدار بالایی خودش است. بنابراین، می‌توان آرایه دوبُعدی ساخت که مقادیر از پیش تولید شده را ذخیره می‌کند. برای تولید یک مقدار در یک خط، می‌توان از مقادیری که پیش‌تر در آرایه ذخیره شده‌اند استفاده کرد.

محاسبه مثلث خیام پاسکال در ++C

محاسبه مثلث خیام پاسکال در C

محاسبه مثلث خیام پاسکال در جاوا

محاسبه مثلث خیام پاسکال در #C

محاسبه مثلث خیام پاسکال در PHP

خروجی

خروجی قطعه کد بالا برای n = 5 به صورت زیر است.

1 
1 1 
1 2 1 
1 3 3 1 
1 4 6 4 1

روش بیان شده را می‌توان به نوعی بهینه کرد که از فضای اضافی (O(n استفاده کند. این کار را می‌توان با توجه به این موضوع انجام داد که برای محاسبه مقادیر یک سطر، تنها نیاز به مقادیر سطر پیشین آن است. بنابراین، می‌توان یک آرایه با اندازه n را ساخت و مقادیر را بازنویسی کرد. در ادامه، راهکار دیگری ارائه شده که تنها از فضای اضافی (O(1 استفاده می‌کند.

روش ۳ با پیچیدگی زمانی (O(n² و فضای اضافی (O(1

این روش، بر مبنای روش اول است. چنانکه پیش‌تر بیان شد، ورودی‌های سطر iاُم در سطر شماره line، ضرایب چندجمله‌ای (C(line, i هستند و همه سطرها با مقدار ۱ شروع می‌شوند. هدف محاسبه (C(line, i با استفاده از (C(line, i-1 است. این مقدار را می‌توان در زمان (O(1 با استفاده از روش زیر محاسبه کرد.

C(line, i)   = line! / ( (line-i)! * i! )
C(line, i-1) = line! / ( (line - i + 1)! * (i-1)! )
می‌توان رابطه زیر را از دو رابطه بالا نتیجه گرفت.
C(line, i) = C(line, i-1) * (line - i + 1) / i

بنابراین، (C(line, i را می‌توان با استفاده از (C(line, i-1 در زمان (O(1 محاسبه کرد.

محاسبه مثلث خیام پاسکال در ++C

محاسبه مثلث خیام پاسکال در C

محاسبه مثلث خیام پاسکال در جاوا

محاسبه مثلث خیام پاسکال در پایتون ۳

محاسبه مثلث خیام پاسکال در #C

محاسبه مثلث خیام پاسکال در PHP

خروجی

خروجی قطعه کد بالا برای n = 5 به صورت زیر است.

1 
1 1 
1 2 1 
1 3 3 1 
1 4 6 4 1

بنابراین، راهکار سوم، نسبت به سایر روش‌های ارائه شده در این مطلب بهتر است. اما ممکن است موجب «سرریز صحیح» (Integer Overflow) برای مقادیر بزرگ n شود؛ زیرا برای به دست آوردن مقادیر، دو عدد صحیح را ضرب می‌کند.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌‌نویسی
• آموزش برنامه‌نویسی C++‎
• مجموعه آموزش‌های ریاضیات
• برنامه تشخیص اعداد اول در پایتون — به زبان ساده
• برنامه تجزیه عدد به عوامل اول آن — به زبان ساده
• حل مساله رنگ‌آمیزی گراف با الگوریتم پس گرد — به زبان ساده

^^