بهینه سازی چند هدفه چیست؟ – راهنمای جامع
«بهینه سازی چند هدفه» (Multi-Objective Optimization)، حوزهای از «تصمیمگیری چند معیاری» (Multi-Criteria Decision Making) محسوب میشود. بهینه سازی چند هدفه با «مسائل بهینهسازی ریاضیاتی» (Mathematical Optimization Problems) سروکار دارد که در آنها نیاز است بیش از یک تابع هدف (Objective Function)، به طور همزمان، بهینهسازی شوند. بهینه سازی چند هدفه با نامهای دیگری نظیر «برنامه ریزی چند هدفه» (Multi-Objective Programming)، «بهینهسازی برداری» (Vector OPtimization)، «بهینهسازی چند معیاری» (Multi-Criteria Optimization)، «بهینهسازی چند مشخصهای» (Multi-Attribute Optimization) یا «بهینهسازی پارتو» (Pareto Optimization) نیز شناخته میشود.


روشهای بهینه سازی چند هدفه در بسیاری از شاخههای علوم و مهندسی به کار گرفته میشوند و زمانی مورد استفاده قرار میگیرند که برای رسیدن به تصمیمات بهینه در سیستم، نیاز است میان دو یا چند هدف متناقض موازنه (Trade-off) برقرار شود. بدون شک در بسیاری از کاربردهای مهندسی، طراحان فرایند و سیستمهای مهندسی بر اساس اهداف متناقض، تصمیمگیری میکنند. به عنوان نمونه، در فرایند طراحی خودرو، علاوه بر اینکه هدف مهندسان طراحی خودرویی است که عملکرد (Performance) حداکثری داشته باشد، به طور همزمان، به دنبال طراحی خودرویی هستند که کمترین میزان آلایندگی و مصرف سوخت را داشته باشد.
در این مورد و موارد مشابه، از آنجایی که بیش از یک تابع هدف باید مورد بررسی قرار بگیرد، نیاز است تا به کارگیری روشهای بهینه سازی چند هدفه مورد بررسی قرار بگیرد. مهمترین ویژگی در چنین روشهایی این است که با بهکارگیری مدلهای بهینه سازی چند هدفه (Multi-Objective Optimization)، بیش از یک جواب کاندید (یک جواب ممکن برای مسأله مورد نظر) در اختیار طراحان و مهندسان سیستم قرار گرفته میشود؛ هر یک از این جوابها، موازنه میان توابع هدف مختلف را نمایش خواهند داد.
حتی برای یک مسأله بهینه سازی چند هدفه ساده، احتمال اینکه جواب بهینهای (Optimal Solution) یافت شود که به طور همزمان، تمامی توابع هدف تعریف شده در مسأله را بهینه سازی کند، بسیار کم است. در بسیاری از موارد، توابع هدف تعریف شده در مسأله بهینه سازی چند هدفه با یکدیگر در تناقض هستند. در چنین حالتی گفته میشود که برای یک مسأله بهینه سازی چند هدفه، «جوابهای بهینه پارتو» (Pareto Optimal Solutions) وجود خواهد داشت (از لحاظ تئوری، ممکن است بینهایت جواب بهینه پارتو برای یک مسأله بهینه سازی چند هدفه وجود داشته باشد). در بخشهای بعدی با مفهوم جواب بهینه پارتو آشنا خواهید شد.
پیش از ادامه این مبحث لازم است یادآور شویم که میتوانید بهینهسازی چندهدفه را با استفاده از مجموعه آموزش بهینهسازی چندهدفه فرادرس یاد بگیرید.

مفهومی به نام جواب نامسلط در سیستمهای حل مسائل بهینه سازی چند هدفه وجود دارد. در صورتی به یک جواب کاندید برای مسأله بهینه سازی چند هدفه، جواب «نامسلط» (Non-Dominated) گفته میشود که بهبود مقادیر تولید شده توسط یک یا چند تابع هدف از این مسأله (از طریق قرار دادن جواب کاندید در توابع هدف و تولید مقادیر خروجی)، سبب کاهش کیفیت مقادیر تولید شده توسط دیگر توابع هدف همان مسأله شود. به چنین جوابهایی، «بهینه پارتو» (Pareto Optimal) گفته میشود. بدون در اختیار داشتن اطلاعات اضافی، تمامی جوابهای بهینه پارتو به یک اندازه خوب هستند و با یکدیگر برابر در نظر گرفته میشوند.
مفهوم برابری (Equivalency) عدم فرومایگی (Non-Inferiority) برای اولین بار توسط ویلفردو پارتو (Vilfredo Pareto) و فرانسیس وای. اجورث (Francis Y. Edgeworth) و در حوزه اقتصاد معرفی شد. از آن زمان تاکنون، مفهوم بهینه سازی چند هدفه، جای پای خود را در حوزه طراحی و مهندسی مستحکم کرده است. ترجمه تحقیقات ویلفردو پارتو به زبان انگلیسی در سال 1971 منجر به پیادهسازی روش بهینه سازی چند هدفه در حوزه مهندسی و «ریاضیات کاربردی» (Applied Mathematics) شد. در طول سه دهه اخیر، بهکارگیری روشهای بهینه سازی چند هدفه در بسیاری از حوزههای مهندسی و طراحی به رشد ثابت خود ادامه داده است. در این مطلب، با مفاهیم ابتدایی در حوزه بهینه سازی چند هدفه آشنا خواهید شد.

مقدمه
شاید تاکنون، بیشتر مسائل بهینهسازی که با آنها برخورد داشتهاید، مسائلی باشند که تنها از یک تابع هدف برخوردار باشند؛ به مدلهایی که برای بهینهسازی این دسته از مسائل مورد استفاده قرار میگیرند، مدلهای «بهینه سازی تک هدفه» (Single-Objective) گفته میشود. در عمل، در بسیاری از مسائل طراحی و مهندسی، بیش از یک تابع هدف وجود دارد. در بسیاری از موارد، توابع هدف تعریف شده در یک مسأله بهینه سازی چند هدفه با یکدیگر در تناقض هستند.
به عنوان نمونه، یک تیم طراحی مهندسی را در نظر بگیرید. در فرایند طراحی، یکی از اهداف تیم طراحی ممکن است کمینه کردن وزن و به طور همزمان، بیشینه کردن قدرت یک مؤلفه ساختاری خاص در محصول در حال طراحی باشد. علاوه بر این، با در نظر گرفتن فرایند طراحی خودرو، اهداف تیم طراحی ممکن است بیشینه کردن عملکرد خودرو (به عنوان نمونه، افزایش خروجی «گشتاور» (Torque) موتور خودرو جهت شتاب بخشیدن به خودرو در بازه زمانی کوتاهتر) و کمینه کردن مصرف سوخت و انتشار آلایندهها باشد؛ دو هدفی که در تناقض با یکدیگر قرار دارند.
دو مثال ذکر شده در بالا، نمونهای از مسائل بهینه سازی چند هدفه هستند که از چند تابع هدف (دو تابع هدف یا بیشتر) تشکیل شدهاند. از نظر ریاضی، یک مسأله بهینهسازی چند هدفه را میتوان را به شکل زیر فرمولبندی کرد:
در این رابطه، یک بردار متشکل از توابع هدف است که به شکل زیر نمایش داده میشود:
همچنین، تعداد توابع هدف در مسأله بهینه سازی چند هدفه را نشان میدهد. پیش از اینکه به طور کامل نحوه تولید جوابهای بهینه پارتو در یک مسأله بهینه سازی چند هدفه شرح داده شود و همچنین، جهت نمایش طبیعت مسائلی که در بهینه سازی چند هدفه با آنها سروکار داریم، ابتدا یک مسأله بسیار ساده در نظر گرفته خواهد شد؛ سادگی این مسأله بهینه سازی چند هدفه از این جهت است که مسأله و جوابهای آن را میتوان به صورت بصری نمایش داد.
مثال اول: یک مسأله بهینه سازی چند هدفه را در نظر بگیرید که به شکل زیر تعریف میشود:
دو تابع هدف و را میتوان در «فضای طراحی» (Design Space) مسأله بهینه سازی چند هدفه، به شکل زیر رسم کرد (در مثال اول، فضای طراحی همان صفحه است):
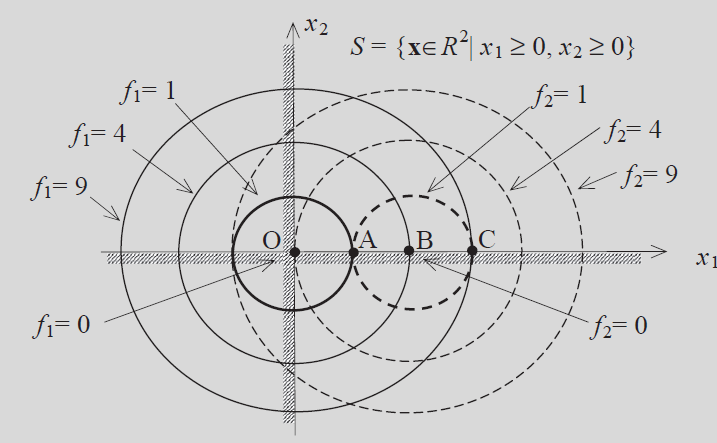
خطوط جدا کننده توابع هدف و (یا همان کانتورهای این توابع) در شکل، دایرههایی هستند که به ترتیب در مرکزیت (0، 0) و (0، 2) قرار دارند. این دو تابع در شکل بالا به ترتیب توسط دایرههای با خطوط توپر و دایرههایی با خطوط خطچین نمایش داده شدهاند. مجموعه جوابهای امکانپذیر (Feasible Set) یا ناحیه جوابهای امکانپذیر این مسأله بهینه سازی چند هدفه، به شکل زیر تعریف میشود:
مجموعه جوابهای امکانپذیر، «ربع» (Quadrant) اول صفحه خواهد بود که در شکل بالا نمایش داده شده است. همان طور که در شکل بالا نیز مشخص است، کمینه (Minimum) تابع در نقطه و کمینه تابع در نقطه رخ میدهد. با این حال، در نقطه مقدار تابع برابر با 4 و در نقطه B، مقدار تابع برابر با 4 است؛ هیچ یک از دو مقدار محاسبه شده، نقطه کمینه توابع و نیستند. کاملا مشخص است که هیچ نقطه خاصی وجود ندارد که سبب شود توابع و در مقدار کمینه خود قرار بگیرند.
بهترین جوابی که تا حدودی میتواند دو تابع را در نقطهای نزدیک به کمینه قرار دهد، در نقطه حاصل میشود؛ در این نقطه، مقدار توابع و برابر با است. اگرچه فاصله گرفتن از این نقطه ممکن است سبب کاهش کیفیت جواب یکی از توابع هدف شود ولی در نقطه مقابل ممکن است سبب افزایش کیفیت جواب تولید شده توسط تابع هدف دیگر شود (ممکن است منجر به تولید مقدار کمینهتری برای تابع هدف دوم شود).
شایان توجه است که برای یک مسأله بهینه سازی چند هدفه نظیر مثال اول، هر جوابی که میان نقاط و قرار بگیرد ممکن است به عنوان یک جواب قابل قبول شناخته شود. زیرا افزایش کیفیت جواب در یکی از توابع هدف مسأله (کمینه کردن تابع اول)، بدون کاهش کیفیت جواب تولید شده توسط تابع هدف دیگر، امکانپذیر نخواهد بود.
البته با تغییر دادن نقاطی که خارج از بخشبندی خطی میان نقاط و قرار دارند (تمامی نقاطی که در محدوده و قرار دارند)، میتوان مقادیر دو تابع هدف و را به طور همزمان کاهش داد. به عنوان نمونه، نقطه را در نظر بگیرد. در این نقطه، مقدار توابع و به ترتیب برابر با و هستند. با حرکت کردن از نقطه به سمت نقطه ، مقدار کمینهتری برای دو تابع و حاصل خواهد شد (افزایش کیفیت جوابها).
شایان توجه است که به نقاط میان و ، که توسط رابطه زیر تعریف میشوند، مجموعه بهینه پارتو (Pareto Optimal Set) برای مسأله بهینه سازی چند هدفه گفته میشود (مجموعه ). یک مجموعه بهینه پارتو معمولا حاوی بینهایت جوابی است که به عنوان جوابهای معتبر برای یک مسأله بهینه سازی چند هدفه شناخته میشوند.
توجه داشته باشید که شاید برای یک مسأله بهینه سازی چند هدفه ساده (مانند مثال اول)، پیدا کردن جوابهای بهینه پارتو کار سادهای باشد، ولی متاسفانه، برای دیگر مسائل بهینه سازی چند هدفه، چنین امری ممکن است ساده نباشد. به طور کلی، صحبت کردن درباره جوابهای بهینه پارتو، تنها در فضای طراحی (Design Space) مسأله بهینه سازی چند هدفه کافی نیست. برای درک بهتر مفهوم مسائل بهینه سازی چند هدفه (و تکنیکهای آن)، لازم است تا مسأله به «فضای معیار» (Criterion Space | فضای هدف) نگاشت شود. در بخش بعدی، با مفاهیم پایه بهینه سازی چند هدفه و فضای معیار بیشتر آشنا خواهید شد.
مفاهیم پایه در بهینه سازی چند هدفه
مفهوم اسکالر (عددی) بودن «بهینگی» (Optimality) مسائل بهینهسازی «تکهدفه» (Single Objective)، به طور مستقیم در بهینه سازی چند هدفه کاربرد ندارد. برای این که بتوان با مفهوم بهینگی در مسائل بهینه سازی چند هدفه آشنا شد، ابتدا باید مفهوم «بهینگی پارتو» (Pareto Optimality) را شرح داد. در این بخش، ابتدا با استفاده از مثال اول، مفاهیمی نظیر فضای طراحی و فضای معیار (یا فضای هدف) شرح داده خواهند شد.
فضای معیار و فضای طراحی در مسائل بهینه سازی چند هدفه
در مثال اول، فضای طراحی یک مسأله بهینه سازی چند هدفه نمایش داده شد. سپس، مجموعه جوابهای امکانپذیر (مجموعه ) تعریف، کانتورهای توابع هدف (خطوط جدا کننده توابع هدف) رسم و در نهایت، مجموعه بهینه پارتو (مجموعه ) این مسأله بهینه سازی چند هدفه در فضای طراحی شناسایی شد.
یک روش ممکن دیگر برای حل مسائل بهینه سازی چند هدفه، استفاده از فضای معیار (Criterion Space) است. متناوبا، یک مسأله بهینه سازی چند هدفه را میتوان در فضایی به نام فضای معیار نمایش داد؛ در این فضا، محورها به وسیله توابع هدف نمایش داده خواهند شد. به عنوان نمونه، شکل زیر نمایش مسأله بهینه سازی چند هدفه مثال اول را در فضای طراحی نمایش میدهد.

شکل زیر، مسأله بهینه سازی چند هدفه مثال اول را این بار در فضای معیار (یا همان صفحه ) نمایش میدهد. همانطور که در شکل زیر مشخص است، محورهای این فضا توسط توابع هدف نشان داده شدهاند.
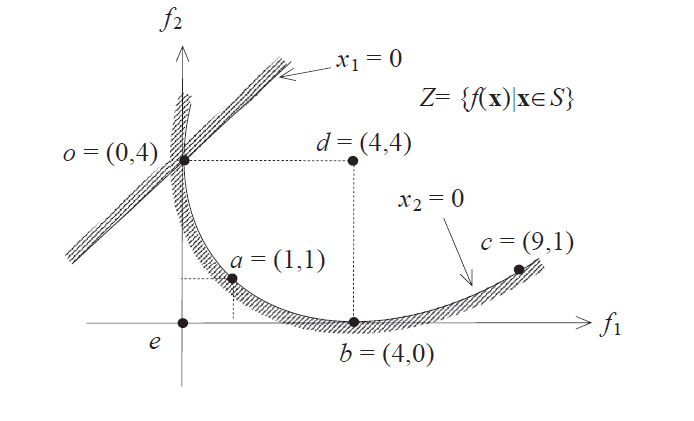
شایان توجه است که قیدهای و در این مسأله بهینهسازی، از طریق حل کردن آنها بر حسب و ، به فضای معیار نگاشت خواهند شد.
فضای معیار امکانپذیر ، در قالب مجموعه مقادیری از تابع هدف، که متناظر با نقاط امکانپذیر (Feasible Points) در فضای طراحی هستند، تعریف میشود:
همانطور که در شکلهای بالا نشان داده شده است، نقاط ، و در فضای طراحی به نقاط ، و در فضای معیار نگاشت شدهاند. مجموعه بهینه پارتو (Pareto Optimum) در فضای طراحی مسأله بهینه سازی چند هدفه، که به شکل تعریف میشود، به منحنی oab در فضای معیار نگاشت و به شکل زیر نمایش داده میشود:
به منحنی oab در فضای معیار، «جواب پارتو» (Pareto Solution)، بهینه پارتو، «جبهه پارتو» (Pareto Front) و یا «مجموعه پارتو» (Pareto Set) گفته میشود؛ منحنی oab نمایش دهنده جواب یک مسأله بهینه سازی چند هدفه محسوب میشود.
همانطور که در شکل نمایشدهنده فضای معیار مثال اول مشخص است، کمینه تابع هدف برابر با 0 است که در نقطه واقع شده است. در سوی مقابل، کمینه تابع هدف برابر با صفر است که در نقطه واقع شده است. علاوه بر این، در صورتی که نیاز باشد تا کمینهسازی بیشتری روی مقادیر تولید شده توسط یکی از توابع انجام شد، بدون شک مقدار تابع دیگر افزایش مییابد.
همچنین، هیچ یک از نقاط دیگری که روی جبهه پارتو قرار دارند نمیتوانند به طور همزمان، کمینهسازی بیشتری رو مقادیر توابع هدف و انجام دهند. با این حال، برای نقطه دیگری، نظیر ، که روی جبهه پارتو قرار ندارد، این امکان وجود دارد که با حرکت دادن این نقطه به سمت جبهه پارتو، مقدار دو تابع هدف و را به طور همزمان کاهش داد.
نکته شایان توجه در مورد مسائل بهینه سازی چند هدفه و تولید فضای طراحی و فضای معیار متناسب با مسأله این است که هر نقطه در فضای طراحی را میتوان به یک نقطه در فضای معیار نگاشت کرد. با این حال، عکس چنین حالتی همیشه صحیح و امکانپذیر نیست؛ به عبارت دیگر، هر نقطه در فضای معیار لزوما متناظر با یک نقطه (یا چند نقطه) در فضای معیار نخواهد بود. به عنوان نمونه، نقطه در فضای معیار به هیچ نقطهای در فضای طراحی نگاشت نخواهد شد. علاوه بر این، نقطه در فضای معیار به دو نقطه و در فضای طراحی نگاشت میشود ( و ).
بهینگی پارتو (Pareto Optimality)
به مفهوم تعریف جوابهای یک مسأله بهینه سازی چند هدفه، بهینگی پارتو (Pareto Optimality) گفته میشود. در صورتی به نقطه در فضای طراحی مسأله () بهینه پارتو گفته میشود که در مجموعه نقطه دیگری وجود نداشته باشد که باعث کمینهسازی حداقل یکی از توابع هدف موجود در مسأله بهینه سازی چند هدفه و به طور همزمان، افزایش مقدار یک تابع هدف دیگر شود.
در مثال اول این مطلب، بهینه پارتو برابر با رابطه زیر خواهد بود:
در ادامه، تعریف دقیقتری از بهینه پارتو ارائه خواهد شد.
تعریف اول: بهینه پارتو (Pareto Optimality)
در صورتی به نقطه در فضای طراحی مسأله () بهینه پارتو گفته میشود که نقطه دیگری مانند وجود نداشته باشد، به طوری که:
برای درک بهتر عبارات بالا، فرض کنید که نقطه یک بهینه پارتو باشد (این نقطه، همان نقطه در فضای طراحی (Design Space) مسأله بهینه سازی چند هدفه مثال اول است). در این نقطه، مقدار تابع و است. حالا، درست بودن شرط زیر را برای یک نقطه دیگر بررسی میکنیم؛ در صورتی که شرط زیر برای نقاط دیگر برقرار باشد، نقطه را نمیتوان به عنوان یک نقطه بهینه پارتو در نظر گرفت:
برای چنین کاری، نقطه را انتخاب میکنیم (این نقطه، همان نقطه در فضای طراحی (Design Space) مسأله بهینه سازی چند هدفه مثال اول است). در این نقطه، است. بنابراین، در نقطه ، شرط بالا به شکل زیر برقرار است.
با توجه به شرطی که در ابتدای تعریف نقاط بهینه پارتو وضع شد، نقطه یک بهینه پارتو نخواهد بود. در نقطه مقابل، در صورتی که نقطه را بعنوان یک نقطه بهینه پارتو فرض کنیم، مقادیر توابع و به ترتیب برابر با خواهد بود. همچنین، هیچ نقطه دیگری وجود ندارد که در آن، مقدار توابع و کمتر از مقدار آنها در نقطه باشد. در نتیجه، نقطه یک نقطه بهینه پارتو خواهد بود. در واقع، تمامی نقاط موجود در مجموعه یا همان مجموعه بهینه پارتو در فضای طراحی، شرط بالا را رعایت میکنند. در نتیجه، تمامی اعضای این مجموعه بهینه پارتو هستند.
شایان توجه است که تمامی اعضای مجموعه بهینه پارتو ، همیشه در مرز (Boundary) فضای معیار قرار خواهند داشت. با فرض اینکه نقاط کمینه منحصر به فرد باشند و تنها دو تابع هدف در مسأله بهینه سازی چند هدفه داشته باشند (همانند مثال اول)، مقدار کمینه دو تابع هدف مسأله، نقاط انتهایی جبهه پارتو را تشکیل خواهند داد (نقطه و در شکل زیر).

یک مفهوم بسیار مرتبط دیگر به بهینگی پارتو، «بهینگی پارتوی ضعیف» (Weak Pareto Optimality) است. در نقاط بهینه پارتوی ضعیف، این امکان وجود دارد که با بهینهسازی برخی از توابع هدف مسأله، کیفیت جوابهای تولید شده توسط دیگر توابع هدف کاهش پیدا نکند.
در ادامه، تعریف دقیقتری از بهینه پارتوی ضعیف ارائه خواهد شد.
تعریف دوم: بهینه پارتوی ضعیف (Weak Pareto Optimality)
در صورتی به نقطه در فضای طراحی مسأله () بهینه پارتوی ضعیف گفته میشود که نقطه دیگری مانند وجود نداشته باشد، به طوری که:
به عبارت دیگر، بیک نقطه در فضای طراحی، بهینه پارتوی ضعیف محسوب میشود اگر، نقطه دیگری وجود نداشته باشد که بتواند به طور همزمان، تمامی توابع هدف موجود در مسأله را بهینه کند (یا به طور همزمان، کیفیت جوابهای تولید شده توسط تمامی توابع هدف را افزایش دهد). با این حال، نقاطی نیز ممکن است وجود داشته باشند که کیفیت برخی از توابع هدف موجود در مسأله را افزایش میدهند ولی مقادیر تولید شده توسط دیگر توابع را بدون تغییر نگه میدارند. مفهوم نقاط بهینه پارتوی ضعیف در شکل زیر نمایش داده شده است.

در این مثال نیز، هدف کمینهسازی دو تابع هدف و است. شایان توجه است که خطوط و ، مرز فضای معیار امکانپذیر را تشکیل میدهند و به ترتیب، توسط خطهای افقی و عمودی نمایش داده شدهاند. در این مثال، تمامی نقاطی که روی خط قرار دارند، نقاط بهینه پارتوی ضعیف هستند. با این حال، تنها نقاط A و C به عنوان نقاط بهینه پارتو شناخته میشوند.
در صورتی که هر نقطهای که رو خط قرار داشته باشد (به غیر از نقطه ) را در نظر بگیرید، نظیر نقطه ، هیچ نقطه دیگری نظیر در فضای معیار امکانپذیر وجود نخواهد داشت که در آن:
بنابراین، نقطه یک بهینه پارتوی ضعیف محسوب میشود. در سوی مقابل، از آنجایی که میتوان حداقل یک نقطه نظیر (به عنوان نمونه، تمامی نقاط روی خط ) پیدا کرد که در آن:
بنابراین، نقطه را نمیتوان یک بهینه پارتو به حساب آورد. به طور مشابه، تمامی نقاطی که رو خط قرار داشته باشد (به غیر از نقطه )، بهینه پارتوی ضعیف محسوب میشوند ولی بهینه پارتو نیستند. نکته مهمی که در این بخش باید به آن اشاره شود این است که یک نقطه بهینه پارتو، یک نقطه بهینه پارتوی ضعیف محسوب میشود ولی عکس آن همیشه صادق نیست؛ به عبارت دیگر، یک نقطه بهینه پارتوی ضعیف، لزوما یک نقطه بهینه پارتو نخواهد بود.
یکی دیگر از مفاهیم موجود در بهینه سازی چند هدفه، نقاط مسلط (Dominated) نامسلط (Non-Dominated) هستند. در ادامه، تعریف دقیقتری از این نقاط ارائه خواهد شد.
تعریف سوم: نقاط مسلط (Dominated) نامسلط (Non-Dominated)
بردار متشکل از توابع هدف نامسلط شناخته میشود، اگر و تنها اگر، بردار دیگری نظیر وجود نداشته باشد، به طوری که:
در غیر این صورت، بردار مسلط شناخته میشود. به طور کلی، بهینگی پارتو به هر دو فضای طراحی (Design) معیار اشاره دارد. علاوه بر این مفاهیم، مفهوم دیگری به نام «نقطه منحصر به فرد» (Unique Point) یا «نقطه ایدهآل» (Utopia Point | Ideal Point) در بهینه سازی چند هدفه وجود دارد. در ادامه، تعریف دقیقتری از نقاط ایدهآل ارائه خواهد شد.
تعریف چهارم: نقطه ایدهآل یا منحصر به فرد (Unique Point)
در صورتی به یک نقطه نظیر در فضای معیار، نقطه ایدهآل یا منحصر به فرد (Unique Point) گفته میشود که:
در این رابطه، پارامتر تعداد توابع هدف موجود در مسأله بهینه سازی چند هدفه را نشان میدهد. نقاط ایدهآل، از طریق کمینهسازی هر یک از توابع موجود در مسأله بهینه سازی چند هدفه، بدون در نظر گرفتن دیگر توابع حاصل میشوند. هر بار که یکی از توابع هدف موجود در مسأله بهینه سازی چند هدفه کمینه میشود، یک نقطه در فضای طراحی و یک مقدار متناظر با آن تابع هدف به دست میآید. به عنوان نمونه، در شکل زیر نقطه نقطه ایدهآل مثال اول محسوب میشود.

به طور کلی، احتمال اینکه مقادیر بهینه تمامی توابع هدف موجود در مسأله بهینه سازی چند هدفه، در یک نقطه یکسان در فضای طراحی قرار بگیرد بسیار پایین و کمیاب است. به عبارت دیگر، یک نقطه در فضای طراحی نمیتواند تمامی توابع هدف موجود در یک مسأله بهینهسازی را کمینه کند. بنابراین، نقطه ایدهآل تنها در فضای معیار وجود خواهد داشت.
علاوه بر این، پیدا کردن نقاط ایدهآل، نظیر در فضای معیار مثال اول (شکل بالا)، کار بسیار سختی است. به همین خاطر است که میگویند نقاط ایدهآل معمولا دست نیافتنی (Unattainable) هستند. در چنین حالتی، بهترین گزینه پیدا کردن جوابهایی (جوابهای بهینه پارتو) است که بیشترین نزدیکی ممکن را به جواب ایدهآل در فضای معیار داشته باشند. به چنین جوابی، جواب متوازن (Compromise Solution) گفته میشود.
به عنوان نمونه، نقطه در شکل بالا، نقطهای در فضای معیار است که منجر به تولید جواب متوازن برای مسأله بهینه سازی چند هدفه مثال اول خواهد شد. میزان نزدیکی میان نقطه ایدهآل و نقاط دیگر در فضای معیار (نقاطی که منجر به تولید جواب متوازن میشوند) را میتوان توسط روشهای متفاوتی تعریف کرد. معمولا نقطهای در فضای معیار یک مسأله بهینه سازی چند هدفه به عنوان جواب متوازن شناخته میشود که فاصله اقلیدسی (Euclidean Distance) آن از نقطه ایده آل کمینه باشد. فاصله اقلیدسی یک نقطه در فضای معیار، از نقطه ایدهآل از طریق رابطه زیر محاسبه میشود:
در این رابطه، یک مؤلفه از نقطه ایدهال در فضای معیار را نمایش میدهد. جوابهای متوازن نیز به عنوان جوابهای بهینه پارتو شناخته میشوند.
تولید مجموعه بهینه پارتو
یک مسأله بهینه سازی چند هدفه ساده نظیر مثال اول را به راحتی میتوان از طریق نگاشت مسأله از فضای طراحی (Design Space) به فضای معیار (Criterion Space) و شناسایی مجموعه جوابهای بهینه پارتو در فضای معیار، به صورت زیر حل کرد:
همچنین، مجموعه بهینه پارتو (در مثال اول) را میتوان به راحتی به فضای طراحی اصلی مسأله نگاشت دوباره کرد:
با این حال، برای مسائل بهینه سازی چند هدفه که پیچیدهتر از مثال اول هستند، چنین کاری امکانپذیر نخواهد بود. بنابراین سؤالی که ممکن است در این بخش پدید آید این است که چگونه میتوان چنین مسائلی را حل کرد؟ یکی از راههای موجود برای حل چنین مسائلی استفاده از رویکردهای Brute-Force است.
مثال دوم: به شکل زیر دقت کنید:

در این بخش با یک مسأله بهینه سازی چند هدفه به نام «هرم» (Pyramid) آشنا خواهید شد. همانطور که در شکل بالا مشخص است، عرض قاعده (Base Width) و ارتفاع (Height) هرم، به ترتیب، توسط و نمایش داده شده است. طول وتر (Chord Length) مثلث نیز برابر با است. توابع هدف مسأله طراحی هرم نیز برابر با کمینه کردن مساحت سطح جانبی و کمینه کردن مساحت کل هرم از طریق دو متغیر عرض قاعده () و ارتفاع () هستند.
همچنین حجم هرم باید بیشتر از 1500 اینچ مکعب باشد و کران بالای اندازه عرض قاعده () و ارتفاع () برابر با 30 اینچ است. از نظر ریاضی، مسأله بهینه سازی چند هدفه هرم به شکل زیر تعریف میشود:
مجموعه امکانپذیر برای این مسأله بهینه سازی، در فضای طراحی آن (در چنین حالتی، صفحه ) و به شکل زیر تعریف میشود:
$$ S = \left \{ ( a , h ) \in R ^ 2 \mid V ( a , b ) = \frac { a ^ 2 h } { 3 } \geq 1500 \;\; a n d \;\; 0<a\leq30, \; 0<h\leq30\right\} $$
مجموعه امکانپذیر در فضای طراحی مسأله بهینه سازی چند هدفه در شکل زیر نمایش داده شده است. همچنین، مقادیر و به ترتیب، نقاط بهینه برای توابع هدف و هستند. شایان توجه است که نقاط بهینه و از طریق حل کردن جداگانه توابع هدف متناظر با آنها در زبان برنامهنویسی متلب (MATLAB Programming Language) به دست آمدهاند.

نگاشت این مسأله بهینه سازی چند هدفه از فضای طراحی به فضای معیار کار بسیار سختی است. همچنین، دوبارهنویسی متغیرهای و در قالب توابعی بر حسب و فرایند بسیار پیچیده و مشکلی است. بنابراین، در این مطلب از روشهای مولد (Generative Method) برای تولید و نمایش جوابهای امکانپذیر و غیرامکانپذیر در فضای معیار استفاده میشود.
برای حل مسأله مورد نظر، ابتدا به ازاء و یک میلیون نقطه تصادفی تولید میشود. سپس، مقدار عددی دو تابع هدف و برای هر نقطه (, ) محاسبه میشود. سپس، حجم هرم محاسبه خواهد شد. در صورتی که مقدار حجم محاسبه شده برای یک نقطه بزرگتر یا مساوی 1500 باشد، نقطهای که به وسیله (, ) نمایش داده میشود، یک نقطه امکانپذیر محسوب خواهد شد؛ در غیر اینصورت، غیرامکانپذیر خواهد بود.
در مرحله بعد، تمامی نقاط امکانپذیر و غیرامکانپذیر به طور جداگانه ذخیره و در فضای معیار (صفحه ) با دو رنگ متفاوت نمایش داده میشوند. نقاطی که در محل تقاطع مناطق با رنگهای مختلف قرار دارند، مرز فضای معیار امکانپذیر هستند. به محض اینکه فضای معیار امکانپذیر شناسایی شد، موقعیت نقاط کمینه توابع هدف و مشخص و جبهه پارتو (Pareto Front) شناسایی میشود. تمامی فرایندهای شرح داده شده در شکل زیر نمایش داده شده است.

مقدار کمینه توابع و به ترتیب برابر یا و است. مقدار کمینه تابع در و حاصل میشود؛ این نقطه به که در شکل زیر نمایش داده شده است بسیار نزدیک است. همچنین، مقدار کمینه تابع در و رخ میدهد که به نقطه به که در شکل مشخص شده است بسیار نزدیک است.

برای صحتسنجی نتایج تولید شده، این رویه با تعداد متفاوت نقاط تصادفی (100 تا یک میلیون) به ازاء و آزمایش شده است. نتایج حاصل از آزمایشات انجام شده در جدول زیر نمایش داده شده است.

نتایج نشان میدهد که وقتی تعداد نقاط نمونه از 10 هزار نمونه بیشتر میود، نتایج تغییر قابل ملاحظه و معناداری نمیکنند. با این حال، اگر فضای معیاری که توسط 10 هزار نمونه تولید شده است رسم شود، مرز مجموعه معیار امکانپذیر یا همان جبهه پارتو (Pareto Front)، دیگر به خوبی قابل شناسایی نخواهد بود (شکل زیر).

اگرچه روشهای مولد روشهای بسیار سادهای برای حل مسائل بهینه سازی چند هدفه هستند، اما عملکرد آنها در مسائل سخت و پیچیده (و حتی مسائل با پیچیدگی متوسط) بسیار ضعیف است. به طور کلی، مسائل مهندسی و طراحی، مسائل بسیار پیچیدهای هستند که حل کردن و ارزیابی توابع آنها، بار محاسباتی بسیار قابل توجهی را میطلبد.
بنابراین، استفاده از روشهای مولد برای حل مسائل بهینه سازی چند هدفه، از لحاظ محاسباتی، امکانپذیر نیست.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشود:
- مجموعه آموزشهای الگوریتمهای بهینهسازی هوشمند
- آموزش تئوری و عملی الگوریتمهای ژنتیک
- مجموعه آموزشهای هوش مصنوعی
- مجموعه آموزشهای الگوریتمهای ژنتیک و محاسبات تکاملی
- الگوریتم بهینهسازی فاخته — از صفر تا صد
- الگوریتم ژنتیک — از صفر تا صد
- الگوریتم کلونی مورچگان — از صفر تا صد
- الگوریتم کرم شب تاب — از صفر تا صد
^^













سلام
خواستم در خصوص ترجمه اصطلاحات بکار برده شده در متن درس دو مورد را اعلام کنم که به نطر می رسد نیاز به بازبینی داشته باشد:
1-ترجمه صحیح «برنامهنویسی چند هدفه» (Multi-Objective Programming)، برنامه ریزی چند هدفه است چون هدف برنامه ریزی بهینه سازی در یک روش عملیاتی است که شاخه ای از تحقیق در عملیات می باشد.
2- در قسمت تعریف سوم: نقاط مغلوب (Dominated) نامغلوب (Non-Dominated) درست ترجمه نشده اند منطور از Dominate جواب غالب و مسلط می باشد و منطور از (Non-Dominated) جواب غیر غالب و نامسلط می باشد .
با سلام و احترام؛
صمیمانه از همراهی شما با مجله فرادرس و ارائه بازخورد سپاسگزاریم.
این مورد اصلاح شد.
برای شما آرزوی سلامتی و موفقیت داریم.
سلام دمتون گررررررم عالی بود عالی
با ادبیاتی بسیار ساده و قابل فهم توضیح دادید
لطفا منابع فارسی برای مطالعه بیشتر معرفی کنید
سلام، وقت شما بخیر؛
متاسفانه در زمینه بهینه سازی چند منظوره یا چند هدفه مطالب و منابع زیادی به زبان فارسی وجود ندارد. ولی مجموعه فرادرس دوره آموزش بهینه سازی چند هدفه در متلب را منتشر کرده است که مفاهیم مربوط به بهینه سازی چند منظوره را به خوبی پوشش میدهد. لینک این آموزش و اطلاعات مربوط به آن را میتوانید در اینجا مشاهده کنید.
از اینکه با مجله فرادرس همراه هستید از شما بسیار سپاسگزاریم.
لطفا مراجعتون رو هم قرار بدید برای کسانی که نیاز به پیگیری و مطالعه بیشتر دارند