شبیه سازی مونت کارلو (Monte Carlo Simulation) – محاسبه انتگرال‌ به روش عددی

«شبیه‌سازی» (Simulation)، روشی برای تولید داده‌های یک پدیده واقعی است که از یک توزیع آماری پیروی می‌کند. هر چند ممکن است داده‌های شبیه‌سازی شده، دقیقا با واقعیت همخوانی نداشته باشند ولی زمانی که دسترسی به اطلاعات و داده‌های یک پدیده‌، بسیار پرهزینه و زمان‌بر باشد، شبیه‌سازی روشی موفق و بخصوص مقرون به صرفه برای مطالعه روی چنین پدیده‌هایی است. ولی روش «مونت کارلو» (Monte Carlo) که برای مطالعه روی سیستم‌های فیزیکی و اقتصادی استفاده می‌شود، از تکرار شبیه‌سازی برای شناخت رفتار یک پدیده استفاده می‌کند.

مونت کارلو نام منطقه‌ای در کشور موناکو است که مرکز شرط‌بندی و بازی‌های قمار  در اروپا محسوب می‌شود. البته لازم به ذکر است که «اولام» (Stanisław Ulam) دانشمند لهستانی و «جان فون نویمان» (John von Neumann) دانشمند مجارستانی-آمریکایی که این روش را ابداع کردند به خاطر نحوه تصادفی بودن تولید داده‌ها، نام آن را مونت کارلو گذاشتند. آن‌ها مشغول مطالعه روی انرژی هسته‌ای و شیوه تصادم پروتون‌ها بودند که متوجه شدند برای محاسبه احتمال همجوشی هسته‌ای، می‌توان از هزاران بار شبیه‌سازی موقعیت‌های برخورد با توزیع آماری استفاده کرد.

روش مونت کارلو (Monte Carlo Method)

ابتدا بهتر است تفاوت روش شبیه‌سازی و روش مونت-کارلو را با یک مثال، بیان کرده تا به درک بهتری از این روش برسیم.

فیلم آموزش شبیه سازی مونت کارلو در اکسل برای مدیریت پروژه در فرادرس

کلیک کنید

شبیه‌سازی نتایج بازی شیر یا خط: براساس یک متغیر تصادفی با توزیع یکنواخت در فاصله (0,1) مقداری را تولید می‌کنیم. اگر این مقدار از ۰.۵ بیشتر باشد نتیجه پرتاب سکه شیر و در غیر اینصورت خط خواهد بود. با این کار بازی پرتاب سکه شبیه‌سازی می‌شود.

روش مونت کارلو: هزار عدد تصادفی از توزیع یکنواخت در فاصله (0,1) تولید می کنیم. تعداد اعدادی که بیشتر از 0.5 هستند، بیانگر تعداد شیرها و آن‌هایی که از 0.5 کمتر هستند تعداد خط‌ها را نشان می‌دهند. پس با تکرار یک عمل شبیه‌سازی می‌توانیم در مورد نااریب بودن سکه مورد بحث نظر بدهیم. یعنی اگر نسبت تعداد شیرها به خط‌ها نزدیک ۱ باشد، رای به نااریب بودن سکه می‌دهیم.

هر چه تعداد تکرار‌ها در شبیه‌سازی برای روش مونت کارلو بیشتر باشد، نتایج حاصله قابل اعتمادتر خواهند بود. یکی از ویژگی‌هایی که روش مونت کارلو دارد، حفظ داده‌های مناسب و حذف داده‌های نامناسب است. که به تکنیک «قبول-رد» (Accept-Reject) شهرت دارد.

مثال ۱

یکی از مشهورترین مثال‌ها برای روش مونت کارلو، محاسبه عدد «پی» ($$\pi$$) است که برای محاسبه محیط یا مساحت دایره به کار می‌رود. البته شیوه‌های دیگری نیز برای محاسبه عدد پی وجود دارد. برای مثال یکی از این شیوه‌ها به سوزن بوفون معروف است. به منظور محاسبه این عدد باید نسبت مساحت یک دایره را به مربع شعاع آن بدست آورد.

$$\pi=\dfrac{area}{radius^2}$$

حال اگر شعاع دایره (Radius) را ۱ انتخاب کنیم، مساحت دایره برابر با عدد پی خواهد شد. اکنون یک مربع با ضلع ۲ را در نظر بگیرید که یک دایره با شعاع ۱ درون آن محاط شده است.

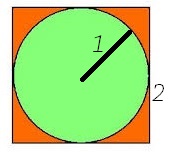
حال به کمک شبیه‌سازی دو متغیر مستقل از توزیع یکنواخت در فاصله $$(-1,1)$$ تولید می‌کنیم. اولی را با x و دومی را با y نشان می‌دهیم. در نتیجه نقاط (x,y) درون مربع قرار می‌گیرند. واضح است که مساحت مربع برابر با 4 است.

نقاط درون دایره باید در رابطه $$x^2+y^2\leq r^2$$‌ صدق کنند، این کار نقاط مورد قبول (Accept) را تعیین می‌کنند. بقیه نقاط نیز جزء گروه نقاط رد (Reject) خواهند بود. پس نسبت تعداد نقاط درون دایره (مساحت دایره) به نقاط تولید شده (مساحت مربع) برابر با یک چهارم عدد پی است، پس کافی است این نسبت را چهار برابر کنیم تا عدد پی بدست آید.

کد تولید شده در زبان برنامه نویسی R برای انجام این محاسبات در ادامه قرار دارد.

1options(scipen=999)
2set.seed(12345)
3in_circle=0
4n=c(100,1000,10000,100000)
5
6print(cat('      Pi','    number of iteration'))
7
8for (i in 1:length(n))
9  {
10    x=runif(n[i],-1,1)
11    y=runif(n[i],-1,1)
12    in_circle=sum(x^2+y^2<1)
13    tot=in_circle/n[i]
14    p=tot*4
15    print(paste(format(p,digits=6,nsmall = 5),format(n[i],digits = 8)))
16}

در این کد، n تعداد تکرار‌ها و x ,y مقدارهای تصادفی از توزیع یکنواخت هستند که توسط شبیه‌سازی با دستور runif ایجاد شده‌اند. خروجی برنامه به صورت زیر است.

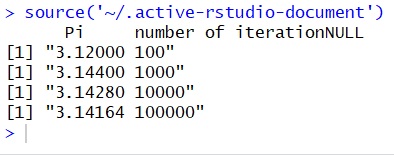
همانطور که دیده می‌شود، برای حدود یک میلیون نقطه شبیه‌سازی شده مقدار عدد پی با سه رقم اعشار صحیح به دست آمده است.

روند حل مسئله در روش مونت کارلو

هر چند روش مونت کارلو، دارای حالت‌های مختلفی است ولی معمولا می‌توان مراحل زیر را برای همه آن‌ها در نظر گرفت:

1. ویژگی‌ داده‌های ورودی مشخص می‌شود. (فاصله ۱- تا ۱ برای اعداد شبیه‌سازی شده به منظور پیدا کردن عدد پی)
2. ورودی، مقدارهایی به عنوان داده‌های تصادفی شبیه‌سازی شده است. (انتخاب توزیع یکنواخت برای تولید اعداد تصادفی برای پیدا کردن عدد پی)
3. انجام محاسبات روی اعداد تصادفی تولید شده (محاسبه رابطه مربوط به دایره)
4. تعیین نقاط قبول و رد در نتیجه شبیه‌سازی (نقاط درون دایره، قبول و نقاط بیرون دایره، رد)
5. جمع‌بندی و نهایی‌سازی محاسبات به منظور دسترسی به پاسخ پرسش اصلی (محاسبه ۴ برابر نسبت مساحت دایره به مربع)

محاسبه انتگرال به روش مونت کارلو

فرض کنید برای محاسبه انتگرال تابع $$h(x)$$ روش تحلیلی وجود ندارد. در همین راستا لازم است برای محاسبه این انتگرال در بازه a تا b از روش‌های عددی کمک گرفت.

فیلم آموزش محاسبه انتگرال با شبیه سازی مونت کارلو در فرادرس

کلیک کنید

بنابراین طبق روش مونت کارلو در فاصله $$(a,b)$$ اعداد تصادفی از توزیع یکنواخت تولید می‌کنیم. سپس تابع $$h(x)$$ را به صورت زیر تغییر می‌دهیم.

$$w(x)=h(x).(b-a)$$

از آنجایی که تابع جرم احتمال برای توزیع یکنواخت به صورت $$f(x)=\dfrac{1}{b-a}$$ نوشته می‌شود، خواهیم داشت:

$$\int_a^bh(x)dx=\int_a^bw(x)f(x)dx=E(w(x))$$

که منظور از $$E(w(x))$$ امید-ریاضی $$w(x)$$‌ است. پس کافی است که متوسط یا میانگین مقدارهای $$w(x)$$ که برای نقاط شبیه‌سازی شده در فاصله a تا b محاسبه شده را بدست آوریم.

مثال ۲

مقدار انتگرال $$h(x)=x^3$$ در فاصله ۰ تا ۱ به روش تحلیلی برابر با $$\dfrac{1}{4}$$‌ است. حال به روش مونت کارلو این محاسبه را انجام می‌دهیم.

ابتدا فرض کنید از توزیع یکنواخت با تابع چگالی $$f(x)=\dfrac{1}{b-a}$$ استفاده خواهیم کرد. انتگرال مورد نظر را به صورت زیر نوشته‌ایم:

$$\int_0^1x^3dx=\int_0^1x^3(b-a)f(x)dx=\int_0^1\dfrac{x^3(1-0)}{(1-0)}dx$$

که همان امید-ریاضی متغیر تصادفی $$X^3$$ است، اگر X از توزیع یکنواخت باشد. طبق قانون اعداد بزرگ،‌ مشخص است میانگین مقدارهای مشاهده شده، برآوردی برای امید-ریاضی $$X^3$$ خواهد بود. بنابراین برای محاسبه این انتگرال مراحل زیر را طی می‌کنیم:

1. محدوده مورد نظر برای داده‌های تصادفی را تعیین می‌کنیم. از آنجایی که حدود انتگرال بین ۰ تا ۱ است، این محدوده را فاصله $$(0,1)$$ در نظر می‌گیریم.
2. ۱۰۰۰ نمونه تصادفی از توزیع یکنواخت در فاصله $$(0,1)$$ تولید می‌کنیم.
3. تابع $$w(x)$$ را برای این نقاط محاسبه می‌کنیم. یعنی همه را به توان ۳ می‌رسانیم.
4. میانگین مقدارهای حاصل از مرحله ۳ را بدست می‌آوریم.

با این کار انتگرال مربوطه محاسبه خواهد شد. کد برنامه محاسباتی به زبان R برای این مسئله در زیر دیده می‌شود. در این برنامه تابعی به نام integral تعریف شده که دارای سه پارامتر n (تعداد نقاط شبیه‌سازی شده)، a (کران پایین انتگرال) و b (کران بالای انتگرال) است.

1set.seed(12345)
2integtal=function(n,a,b)
3{
4  random=runif(n,a,b)
5  wx=random^3*(b-a)
6  integ=mean(wx)
7}
8a=0
9b=1
10n=1000
11integralval=integtal(n,a,b)
12integralval

درون برنامه، تابع integral با پارامترهای 1000، 0 و 1 اجرا شده است. نتیجه نیز بر این اساس، برابر با 0.2583 خواهد بود که اندکی با 0.25 که مقدار تحلیلی محاسبه انتگرال مورد نظر است، اختلاف دارد.

البته توجه داشته باشید خط اول $$set.seed (12345)$$، برای کنترل اعداد تصادفی در کد نوشته شده تا نتایج بدست آمده از روی داده‌های تصادفی یکسان باشد. در صورتی که آن را حذف کنید، با هر بار اجرای کد برنامه نتایج متفاوت ولی نزدیک به هم خواهید گرفت.

اگر مطلب بالا برای‌تان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آزمایش تصادفی، پیشامد و تابع احتمال
• آموزش محاسبه انتگرال به کمک شبیه سازی مونت کارلو
• شبیه سازی سیستم با سیمیولینک
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های نرم‌افزارهای آماری

^^