مدیریت مقادیر پرت با تابع Outlier در اکسل — راهنمای کاربردی (+ دانلود فیلم آموزش گام به گام)

یک مقدار پرت یا به اصطلاح «Outlier»، مقداری است که از بیشتر داده‌های موجود در لیست بسیار بیشتر یا بسیار کمتر است. زمانی که از اکسل برای بررسی داده‌های خود استفاده می‌کنید، این مقادیر پرت می‌توانند نتیجه را به سمت دیگری سوق دهند. برای مثال ممکن است مقدار متوسط مجموعه‌ای از داده‌ها دقیقا منعکس کننده‌ی مقادیر شما باشد. اکسل تعدادی تابع کاربردی در اختیار شما قرار داده است تا با استفاده از آن‌ها بتوانید این مقادیر را مدیریت کنید. در ادامه نگاهی به این توابع می‌اندازیم.

یک مثال سریع

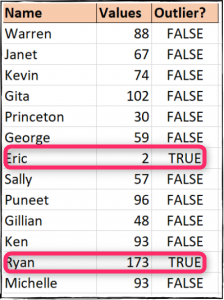
در تصویر زیر، مقادیر پرت به سادگی قابل مشاهده هستند. مقدار 2 به «Eric» و مقدار 173 نیز به «Ryan» نسبت داده شده است.

فیلم آموزش اکسل – محاسبات ریاضی و ماتریسی با Microsoft Excel 2016 در فرادرس

کلیک کنید

در یک مجموعه داده‌ای نظیر شکل زیر، پیدا کردن و مدیریت مقادیر پرت به صورت دستی کاری آسان است.

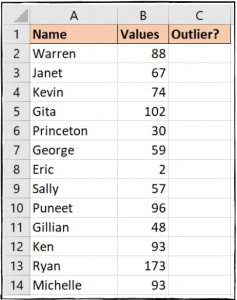
در یک مجموعه داده‌ای بزرگتر، ممکن است شرایط طور دیگری باشد. پیدا کردن و حذف این مقادیر از محاسبات آماری بسیار ضروری است و به همین دلیل است که در این مطلب به چنین مساله‌ای پرداخته‌ایم.

پیدا کردن مقادیر پرت در داده‌ها

برای پیدا کردن مقادیر پرت در یک مجموعه داده‌ای، گام‌های زیر را دنبال کنید:

1. چارک اول و سوم داده‌های خود را حساب کنید (در ادامه بیشتر توضیح خواهیم داد).
2. محدوده‌ی بین چارک اول و سوم را محاسبه کنید (در ادامه بیشتر توضیح خواهیم داد).
3. کران بالا و کران پایین مجموعه داده‌ای خود را حساب کنید.
4. با استفاده از این کران‌ها، مقادیر پرت را پیدا نمایید.

فیلم آموزش جداول محوری در اکسل یا پیوت تیبل Pivot Tables در فرادرس

کلیک کنید

جدولی که در سمت راست تصویر زیر قرار داده‌ایم برای نگه‌داری این مقادیر خواهد بود.

گام اول: محاسبه ربع‌های داده‌ها

اگر داده‌های خود را به چهار بخش تبدیل کنید، نقاط برش دهنده را چارک می‌نامند. %25 کمترین مقادیر از چارک اول کوچکترند، %25 بعدی در ربع دوم هستند که بین چارک دوم و سوم قرار دارند و الی آخر. دلیل استفاده از این روش این است که مرسوم‌ترین تعریف موجود برای مقادیر پرت داده‌هایی هستند که 1.5 برابر از محدوده بین چارک اول کمتر و 1.5 برابر از محدوده بین چارک سون بیشتر هستند. برای پیدا کردن این مقادیر، ابتدا باید ربع‌های خود را پیدا کنیم. برای پیدا کردن آن‌ها، ابتدا باید بدانیم چارک‌های ما به چه شکل هستند.

اکسل یک تابع به نام «QUARTILE» دارد که چارک‌ها داده‌های شما را حساب می‌کند. این تابع دو مقدار نیاز دارد. مقدار اول «array» و مقدار دوم «quart» است.

«array» محدوده داده‌هایی است که در حال محاسبه آن‌ها هستید و «quart» نیز عدد چارک است که می‌خواهید حساب شود (برای مثال عدد 1 گویای چارک اول، عدد 2 گویای چارک دوم و الی آخر).

توجه داشته باشید که در اکسل 2010 مایکروسافت توابع «QUARTILE.INC» و «QUARTILE.EXC» را به عنوان نسخه‌های بهبود یافته تابع «QUARTILE» عرضه کرده است، ولی استفاده از تابع «QUARTILE» بهتر است، چراکه امکان اجرا شدن در نسخه‌های قدیمی‌تر اکسل را دارد.

مجددا به جدول خود نگاهی می‌اندازیم.

برای محاسبه چارک اول، فرمول زیر را در سلول «F2» قرار می‌دهیم.

1=QUARTILE(B2:B14,1)

در حین پر کردن مقادیر، اکسل لیستی از گزینه‌های ممکن برای آرگومان «quart» ارائه می‌دهد.

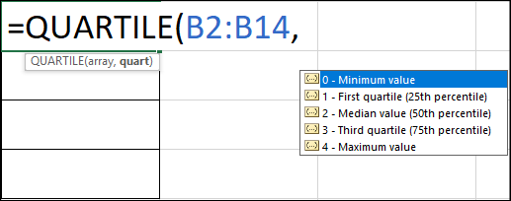
برای محاسبه چارک سوم نیز از فرمول زیر در سلول «F3» استفاده می‌کنیم:

1=QUARTILE(B2:B14,3)

حال چارک داده‌های خود را در جدول مشاهده می‌کنیم.

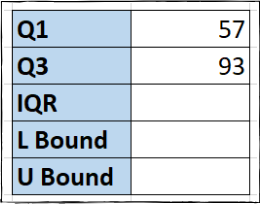
گام دوم: ارزیابی محدوده میان چارکی

دامنه یا برد میان چارکی یا «IQR»، ‏50% مقدار بین چارک اول و سوم مقادیر داده‌های شما است. این مقدار بر اساس تفاوت بین چارک اول و چارک سوم به دست می‌آید.

ما از یک فرمول خیلی ساده در سلول «F4» استفاده می‌کنیم که مقدار چارک اول را از چارک سوم کم می‌کند:

1=F3-F2

حال برد میان چارکی ما به دست آمده است.

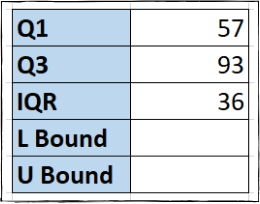
گام سوم: به دست آوردن کران بالا و کران پایین

کران بالا و کران پایین، بیشترین و کمترین مقادیر موجود در مجموعه داده‌ای ما هستند که می‌خواهیم مورد استفاده قرار دهیم. هر مقداری کمتر یا بیشتر از این محدوده، مقادیر پرت ما به حساب می‌آیند.

برای محاسبه کران پایین در سلول «F5»، مقدار «IQR» را ضرب در 1.5 کرده و سپس آن را از مقدار «Q1» کم می‌کنیم:

1=F2-(1.5*F4)

استفاده از پرانتز در این فرمول ضروری نیست چراکه در هر صورت ضرب نسبت به تفریق مقدم است، ولی این کار باعث خواناتر شدن فرمول ما می‌شود.

برای به دست آوردن کران بالا در سلول «F6»، مقدار «IQR» را مجددا ضرب در 1.5 می‌کنیم و سپس آن را با مقدار «Q3» جمع می‌زنیم:

1=F3+(1.5*F4)

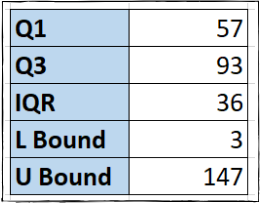
گام چهارم: پیدا کردن مقادیر پرت

حال که تمام داده‌های مورد نیاز خود را به دست آورده‌ایم، زمان پیدا کردن مقادیر پرت است؛ داده‌هایی که از کران پایین کمتر و از کران بالا بیشتر هستند.

برای این کار از تابع «OR» استفاده می‌کنیم تا یک بررسی منطقی انجام دهیم و مقادیری که این شرط را ندارند به دست بیاوریم. فرمول زیر را در سلول «C2» می‌نویسیم:

1=OR(B2<$F$5,B2>$F$6)

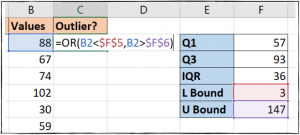
سپس این فرمول را در سلول‌های «C3» تا «C14» اعمال می‌کنیم. مقدار «TRUE» نشان دهنده‌ی مقادیر پرت ما است. همانطور که مشاهده می‌کنید دو مقدار پرت داریم.

نادیده گرفتن مقادیر پرت به هنگام حساب کردن مقدار متوسط

تابع «QUARTILE» به ما امکان محاسبه «IQR» و کار کردن با مرسوم‌ترین تعریف موجود از مقدار پرت را می‌دهد. با این حال برای محاسبه مقدار متوسط یک محدوده بدون در نظر گرفتن «outlier»ها، یک تابع بسیار سریع و آسان‌تر وجود دارد. این روش دیگر مقادیر پرت را برای ما شناسایی نمی‌کند، ولی به ما در انتخاب مقادیر پرت انعطاف‌پذیری بیشتری می‌دهد.

فیلم آموزش استفاده از توابع و فرمول نویسی در اکسل Excel در فرادرس

کلیک کنید

این تابع «TRIMMEAN» نام دارد و با استفاده از فرمول زیر می‌توان آن را پیاده‌سازی کرد:

1=TRIMMEAN(array, percent)

مقدار «array» محدوده مقادیر است که می‌خواهید محاسبه کنید. مقدار «percent» نیز درصد داده‌هایی است که از بالا و پایین مجموعه داده‌ها باید حذف شود.

ما فرمول زیر را در سلول «D3» نوشته‌ایم تا مقدار متوسط را با حذف ۲۰٪ اعدادی که بیشترین یا کمترین مقدارها را دارند، به دست بیاوریم:

1=TRIMMEAN(B2:B14, 20%)

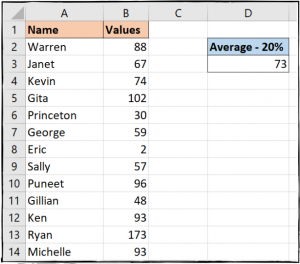
با استفاده از فرمول‌های بالا هم می‌توانید اعداد پرت را شناسایی کنید و هم در صورت نیاز می‌توانید تنها متوسط آن‌ها را بدون در نظر گرفتن اعداد خارج از محدوده به دست بیاوریم.

اگر این مطلب برای شما مفید بوده است،‌ آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های نرم‌افزار مایکروسافت اکسل
• آموزش استفاده از توابع و فرمول نویسی در اکسل
• آموزش‌های مجموعه نرم‌افزاری آفیس
• آموزش تشخیص داده‌های پرت یا Outlier Detection
• کاربرد انواع نمودارها و گراف‌‌ها در اکسل

^^