فرادرسمعادله خط — به زبان ساده
معادلات خطی به روابطی اطلاق می‌شوند که توصیف کننده خط راست باشند. برای نمونه تمامی روابط زیر، معادلاتی خطی را نشان می‌دهند.
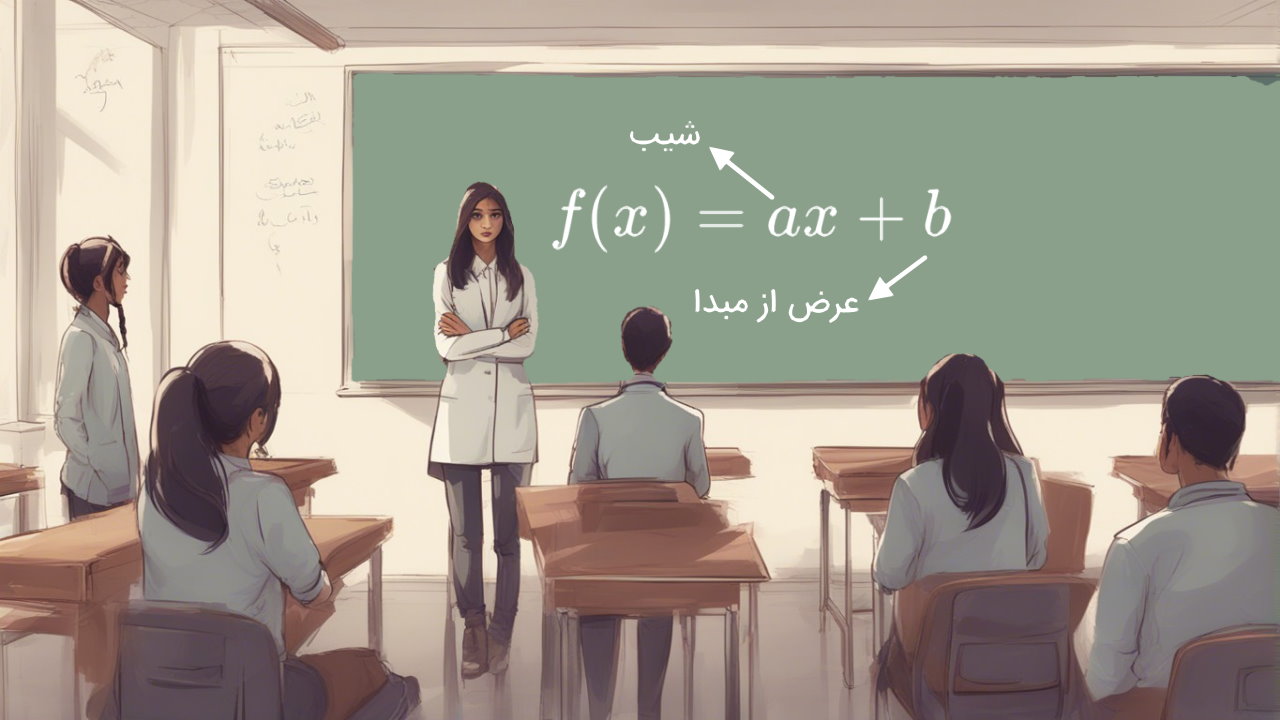
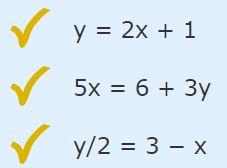
به عنوان مثال تابع زیر را در نظر بگیرید:
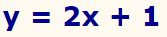
شکل این تابع به‌صورت زیر است:
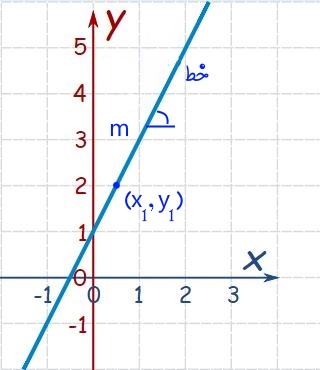
در شکل بالا:
- اگر x افزایش یابد، y به اندازه‌ای دوبرابر افزایش می‌یابد. در نتیجه به عبارت 2x نیاز است.
- زمانی که x برابر با ۰ باشد، y برابر با ۱ است. بنابراین به ۱+ نیز نیاز داریم.
- با توجه به دو گذاره بالا رابطه تابع مربوط به شکل فوق برابر با y=2x+1 است.
در زیر مقادیری از این تابع، محاسبه شده‌اند.
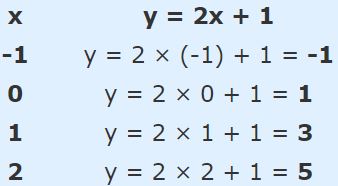
می‌توانید چک کنید و ببینید که نقاط بدست آمده در فوق، روی نمودار شکل ۱ قرار می‌گیرند.
شکل‌های مختلف
یک معادله خطی را می‌توان به شکل‌های مختلفی نمایش داد.
در ادامه این مطلب از مجله فرادرس، حالت‌های مختلفی از یک معادله خطی نشان داده شده است.
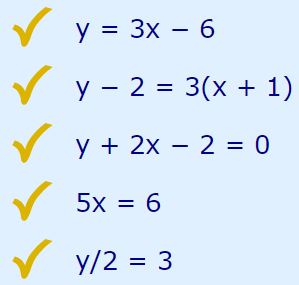
نکته بسیار مهم در روابط بالا این است که در آن‌ها کمیت‌های x,y بصورت توانی، رادیکالی، توان سوم و غیره نیستند. برای نمونه روابطی به شکل زیر خطی محسوب نمی‌شوند:
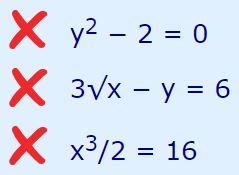
شیب و عرض از مبدأ خط
معمول‌ترین شکل نمایش یک تابع -یا همان معادله- خطی با شیب و عرض از مبدأ است. در حقیقت شیب و عرض از مبدأ خطی به شکل زیر به‌ترتیب برابر با m و b است.
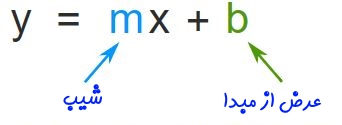
در شکل زیر شیب و عرض از مبدأ مرتبط با تابع فوق نشان داده شده.
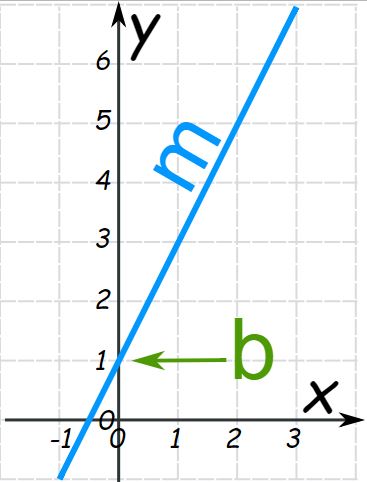
برای نمونه شیب و عرض از مبدأ در نمودار بالا به‌ترتیب برابر با ۲ و ۱ هستند.
شیب و نقطه
یکی دیگر از روش‌های معمول نشان دادن یک معادله خطی، استفاده از شیب و یک نقطه از آن خط است. برای نمونه شکل زیر یک نقطه و شیب خط فرضی را نشان می‌دهد.
با توجه به نقاط مشخص شده در فوق، رابطه این خط را می‌توان به‌صورت زیر بیان کرد:
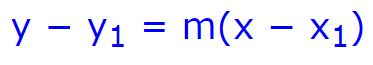
برای نمونه رابطه زیر، مربوط به یک خط است.
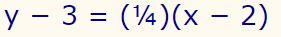
با توجه رابطه فوق، شیب خط مرتبط با رابطه فوق برابر با ۱/۴ و نقطه (۲,3) روی آن قرار گرفته است.
شکل عمومی رابطه مربوط به خط
در بالا شکل‌های متداول برای نمایش یک رابطه خطی را بیان کردیم. اما شکل کلی -یا عمومی- یک خط، به‌شکل زیر است.
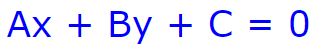
توجه داشته باشید که در رابطه بالا هر دو مقدار A و B نمی‌توانند به‌صورت همزمان برابر با ۰ باشند. جهت توضیح این مفهوم، رابطه زیر را در نظر بگیرید:
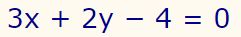
در این رابطه ثوابت عمومی معادله خطی برابر هستند با:
البته توجه داشته باشید که به‌غیر از روش‌های مطرح شده، راه‌های دیگری نیز جهت نشان دادن یک رابطه خطی وجود دارد که معمول نیستند.
معادله در قالب رابطه خطی
همان‌گونه که احتمالا تاکنون متوجه شده‌اید یک تابع خطی و معادله خطی، برابر با یکدیگر هستند. برای نمونه دو عبارت زیر معادل با یکدیگر هستند.
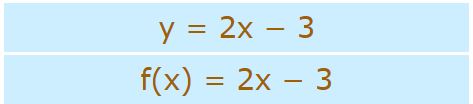
البته توجه داشته باشید که می‌توان از هر نمادی جهت نشان دادن تابع و متغیر استفاده کرد. در زیر ۳ رابطه ارائه شده معادل با یکدیگر هستند.
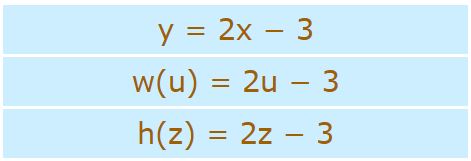
تابع همانی
در معادلات خطی، توابعی وجود دارند که دارای ویژگی‌های خاصی هستند.
این تابع برابر است با:
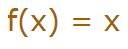
در شکل زیر نمودار مربوط به این رابطه نشان داده شده.
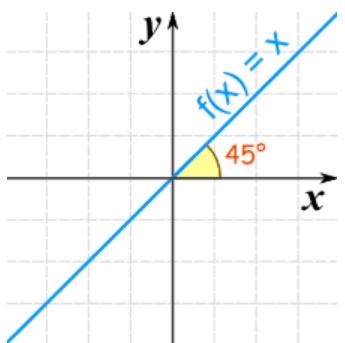
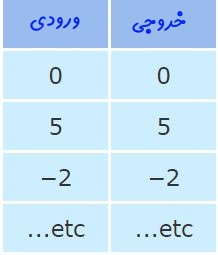
به تابع ارائه شده در بالا، «تابع همانی» (Identity Function) گفته می‌شود. دلیل این نامگذاری، برابر بودن مقدار ورودی و خروجی است. جدول زیر چندین ورودی و خروجی مربوط به این تابع را نشان می‌دهد.
توابع ثابت
شکل خاصی از توابع هستند که در آن‌ها به ازای هر مقدارِ ورودی، عدد ثابتی را به‌عنوان خروجی می‌گیریم. رابطه مربوط به چنین توابعی به‌صورت زیر هستند.
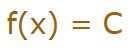
هم‌چنین شکل این توابع، مشابه با تصویر زیر هستند.
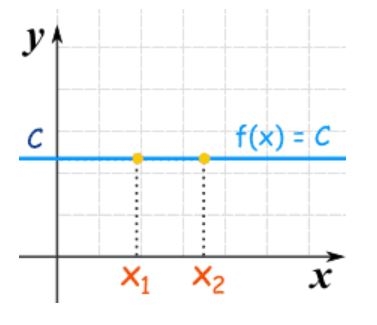
برای نمونه در رابطه بالا به ازای هر ورودی x، خروجی برابر با C است.
ممنون از توضيحاتتون
ممنون از توضيحاتتون واقعا عالى بود
فوق العاده مثل همیشه خدا قبول کنه ازتون
محشره ❤
بسیار عالی توضیح داده متشکرم