جست و جوی هیوریستیک (Heuristic Search) در پایتون — راهنمای کاربردی

«جست و جوی هیوریستیک» (Heuristic Search) که به آن «جست و جوی کاشف» یا «جست و جوی ابتکاری» نیر گفته می‌شود، یکی از انواع روش‌های مورد استفاده در علوم کامپیوتر، «هوش مصنوعی» (Artificial Intelligence) و بهینه‌سازی ریاضیاتی است که به حل سریع‌تر مسائل کمک می‌کند. در این مطلب، اصول جست و جوی هیوریستیک که بخش جدایی ناپذیری از هوش مصنوعی هستند مورد بررسی قرار می‌گیرد. در اینجا، به روش‌های گوناگون هیوریستیک، شامل «مسائل ارضای محدودیت» (Constraint Satisfaction Problems)، «تپه نوردی» (Hill Climbing) و «تبرید شبیه‌سازی شده» (Simulated Annealing) پرداخته می‌شود. همچنین، الگوریتم مسائل ارضای محدودیت (CSP) با استفاده از زبان پایتون پیاده‌سازی می‌شود.

جست و جوی هیوریستیک چیست؟

جست و جوی ابتکاری، روشی است که در حل مسائل، نسبت به روش‌های کلاسیک سریع‌تر عمل می‌کند. جست و جوی کاشف یا ابتکاری، هنگامی که روش‌های کلاسیک در ارائه پاسخ مساله ناتوان هستند، یک راهکار تخمینی برای مساله می‌یابد. این روش، نوعی میانبر برای حل مسائل است، زیرا کاربران معمولا در تلاش برای ایجاد موازنه‌ای میان سرعت و «بهینگی» (Optimality)، «کامل بودن» (Completeness)، «صحت» (Accuracy) یا «دقت» (Precision) هستند.

فیلم آموزش هوش مصنوعی – مقدماتی در فرادرس

کلیک کنید

یک هیوریستیک (یا تابع هیوریستیک)، شباهتی به الگوریتم‌های جست و جو دارد. در هر گام «انشعاب» (Branching)، اطلاعات موجود را ارزیابی می‌کند و تصمیمی بر اساس اینکه کدام شاخه را دنبال می‌کند می‌گیرد. الگوریتم این کار را با رتبه‌بندی جایگزین‌ها انجام می‌دهد. هیوریستیک، معمولا در انواع مسائل موثر است، اما الزاما در همه مسائل کار نمی‌کند.

چرا به هیوریستیک نیاز است؟

یکی از دلایل نیاز به روش هیوریستیک، ارائه راهکاری در زمان منطقی است که برای مساله مطرح به اندازه کافی خوب باشد. نیازی نیست که خروجی این روش بهترین باشد، زیرا به دلیل داشتن سرعت کافی، بیشتر یک راهکار تخمینی محسوب می‌شود. اغلب مسائلی که از هیوریستیک در آن‌ها استفاده می‌شود، «نمایی» (Exponential) هستند.

فیلم آموزش الگوریتم بهینه سازی سیاه چاله BH در فرادرس

کلیک کنید

جست و جوی هیوریستیک امکان کاهش این میزان را به یک عدد چند جمله‌ای می‌دهد. از روش‌های جست و جوی هیوریستیک به این دلیل در هوش مصنوعی استفاده می‌شود که می‌توان از آن‌ها در شرایط‌های گوناگونی بهره برد که امکان استفاده از الگوریتم‌های شناخته شده دیگر وجود ندارد. می‌توان گفت که روش‌های هیوریستیک، روش‌هایی ضعیف محسوب می‌شوند، زیرا نسبت به «انفجار ترکیبی» (Combinatorial Explosion) آسیب‌پذیر هستند.

روش‌های جست و جوی هیوریستیک در هوش مصنوعی

به طور کلی، می‌توان روش‌های جست و جوی هیوریستیک را در دو دسته روش‌های «ضعیف» (Weak Techniques) و «مستقیم» (Direct Techniques) قرار داد. در ادامه به هر یک از این موارد پرداخته خواهد شد.

فیلم آموزش هوش مصنوعی – مقدماتی در فرادرس

کلیک کنید

روش‌های جست و جوی هیوریستیک مستقیم

«جست و جوی ناآگاهانه» یا «جست و جوی کور»‌ (Blind Search)، «جست و جوی غیر مطلع» (Uninformed Search) و «استراتژی کنترل ناآگاهانه» (Blind Control Strategy) نام‌های دیگری هستند که برای روش‌های جست و جوی هیوریستیک مستقیم مورد استفاده قرار می‌گیرند. بهره‌گیری از این روش‌ها همیشه امکان‌پذیر نیست، زیرا نیاز به حافظه یا زمان بیشتری دارند. روش‌های جست و جوی ناآگاهانه، کل «فضای حالت» (State Space) را به دنبال یک راهکار، جست و جو و از یک ترتیب دلخواه از عملیات استفاده می‌کنند. مثالی از این الگوریتم‌ها، «جست و جوی اول سطح» (Breadth First Search | BFS) و «جست و جوی اول عمق» (Depth First Search | DFS) هستند.

روش‌های جست و جوی هیوریستیک ضعیف

«جست و جوی آگاهانه» یا «جست و جوی مطلع» (Informed Search)، «جست و جوی ابتکاری» یا «جست و جوی هیوریستیک» (Heuristic Search) و «استراتژی کنترل هیوریستیک» (Heuristic Control Strategy) اسامی دیگری هستند که برای روش‌های «جست و جوی ضعیف» (Weak Heuristic Search) مورد استفاده قرار می‌گیرند. این روش‌ها، در صورتی که روی نوع صحیحی از مسائل اعمال شوند موثر واقع می‌شوند و معمولا نیاز به نوع خاصی از اطلاعات ویژه دامنه دارند.

فیلم آموزش یادگیری ماشین در فرادرس

کلیک کنید

به این اطلاعات مازاد برای محاسبه کارایی در میان گره‌های فرزند به منظور اکتشاف و بسط دادن آن‌ها نیاز است. هر گره دارای یک تابع هیوریسیتک اختصاص یافته به آن است. مثال‌هایی از این نوع جست و جو عبارتند از «جست و جوی اول بهترین» (BFS | ) و *A. پیش از آنکه روش‌های خاصی تشریح شوند، در ادامه، لیستی از محبوب‌ترین روش‌های جست و جوی هیوریستیک ضعیف آورده شده و سپس، برخی از مهم‌ترین آن‌ها تشریح شده‌اند.

• جست و جوی اول بهترین
• جست و جوی *A
• جست و جوی دوجهته (Bidirectional Search)
• جست و جوی ممنوعه (Tabu Search)
• تپه نوردی
• مسائل ارضای محدودیت

الگوریتم تپه‌نوردی در هوش مصنوعی

در ادامه، الگوریتم تپه نوردی در هوش مصنوعی مورد بررسی قرار می‌گیرد. این الگوریتم، یک روش هیوریستیک برای مسائل بهینه‌سازی ریاضیاتی است. در الگوریتم تپه نوردی، نیاز به انتخاب یک مقدار از ورودی برای بیشینه یا کمینه کردن تابع واقعی است.

فیلم آموزش هوش مصنوعی – تکمیلی در فرادرس

کلیک کنید

این مساله در صورتی که راهکار بیشینه بهینه سراسری نباشد، مناسب محسوب می‌شود. یک مثال شناخته شده برای این نوع الگوریتم، مساله «فروشنده دوره گرد» (Travelling Salesman Problem) است. در این مساله، باید فاصله‌ای که فروشنده می‌پیماید را به حداقل رساند.

ویژگی‌های الگوریتم تپه نوردی

در ادامه، برخی از ویژگی‌های الگوریتم تپه نوردی بیان شده است.

• تپه نوردی، نوعی از الگوریتم‌های «آزمون و خطا» (Generate-and-Test) است.
• در این روش، از رویکرد حریصانه استفاده می‌شود. این یعنی، الگوریتم به تولید راهکاهای حریصانه تا هنگامی ادامه می‌دهد که راهکار مورد نظر خود را بیابد و تنها در جهتی حرکت کند که تابع هزینه را برای آن بهینه می‌کند.

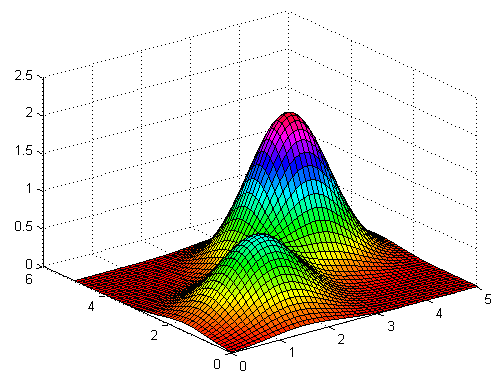
انواع تپه نوردی در هوش مصنوعی

انواع الگوریتم تپه نوردی در ادامه بیان شده است.

• تپه نوردی ساده (Simple Hill Climbing): این روش یک همسایگی گره را در هر زمان بررسی می‌کند و اولین گره‌ای که «هزینه» (Cost) کنونی را بهینه می‌کند به عنوان گره بعدی انتخاب می‌کند.
• تپه نوردی سریع‌ترین صعود (Steepest Ascent Hill Climbing): این روش، همه گره‌های همسایگی را بررسی می‌کند و نزدیک‌ترین گره به حالت راهکار را انتخاب می‌کند.
• تپه نوردی تصادفی: در این روش، الگوریتم یک گره همسایگی را به صورت تصادفی انتخاب می‌کند و تصمیم می‌گیرد که آیا به آن گره حرکت کند و یا گره دیگری را بررسی کند.

الگوریتم تپه نوردی ساده در ادامه آمده است:

۱.حالت اولیه را ارزیابی کن، اگر حالت هدف بود، توقف کن و موفقیت را بازگردان. در غیر این صورت، حالت اولیه را به حالت جاری تغییر بده.

۲. تا هنگام رسیدن به راهکار و یا تا زمانی که هیچ عملگر جدیدی برای اعمال روی حالت جاری باقی نمانده باشد:

الف. یک عملگر جدید برای اعمال روی جاری مولد حالت جدید انتخاب کن.

ب. حالت جدید را ارزیابی کن:

• اگر حالت هدف بود، توقف کن و موفقت را بازگردان.
• اگر حالتی بهتر از حالت جاری بود، آن را به حالت جاری تغییر بده و پردازش کن.
• حتی اگر حالتی بهتر از حالت جاری نبود، تا زمانی که به راهکار برسی ادامه بده.

۳. خروج

مشکلات الگوریتم تپه نوردی

الگوریتم تپه نوردی معمولا دارای سه مشکل است:

فیلم آموزش هوش مصنوعی – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

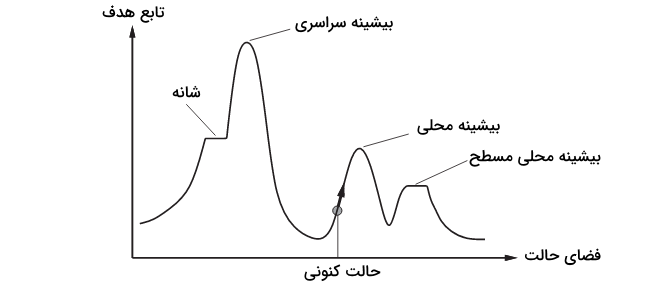
بیشینه محلی (Local Maximum): همه حالات همسایگی دارای مقداری بدتر از مقدار کنونی هستند. رویکرد حریصانه از یک حالت خوب به یک حالت بدتر حرکت نمی‌کند. این موجب می‌شود که فرآیند متوقف شود، حتی اگر راهکارهای خیلی بهتری وجود داشته باشد. «بازگشت به عقب» یا «عقب نشینی» (Backtracking) راهکاری است که در چنین شرایطی مورد استفاده قرار می‌گیرد.

فلات (Plateau): همه همسایگی‌ها دارای مقدار یکسانی هستند. این موجب می‌شود که انتخاب یک جهت غیر ممکن باشد. برای اجتناب از این امر، به طور تصادفی یک پرش بزرگ انجام می‌شود.

خط‌الراس (Ridge): در راس، حرکت در همه جهت‌های ممکن رو به پایین است. این موجب می‌شود که مانند قله به نظر برسد و فرایند متوقف شود. برای اجتناب از این امر، پیش از آزمون (تست) از دو یا تعداد بیشتری قاعده استفاده می‌شود.

مسائل ارضای محدودیت (CSP)

منظور از Constraint همان Limitation یا Restriction و در واقع محدودیت است. در کار با هوش مصنوعی، گاه نیاز می‌شود که برخی از محدودیت‌ها برای حل مساله ارضا شوند. در ادامه، با استفاده از این روش یک مساله حل می‌شود.

فیلم آموزش هوش مصنوعی – تکمیلی در فرادرس

کلیک کنید

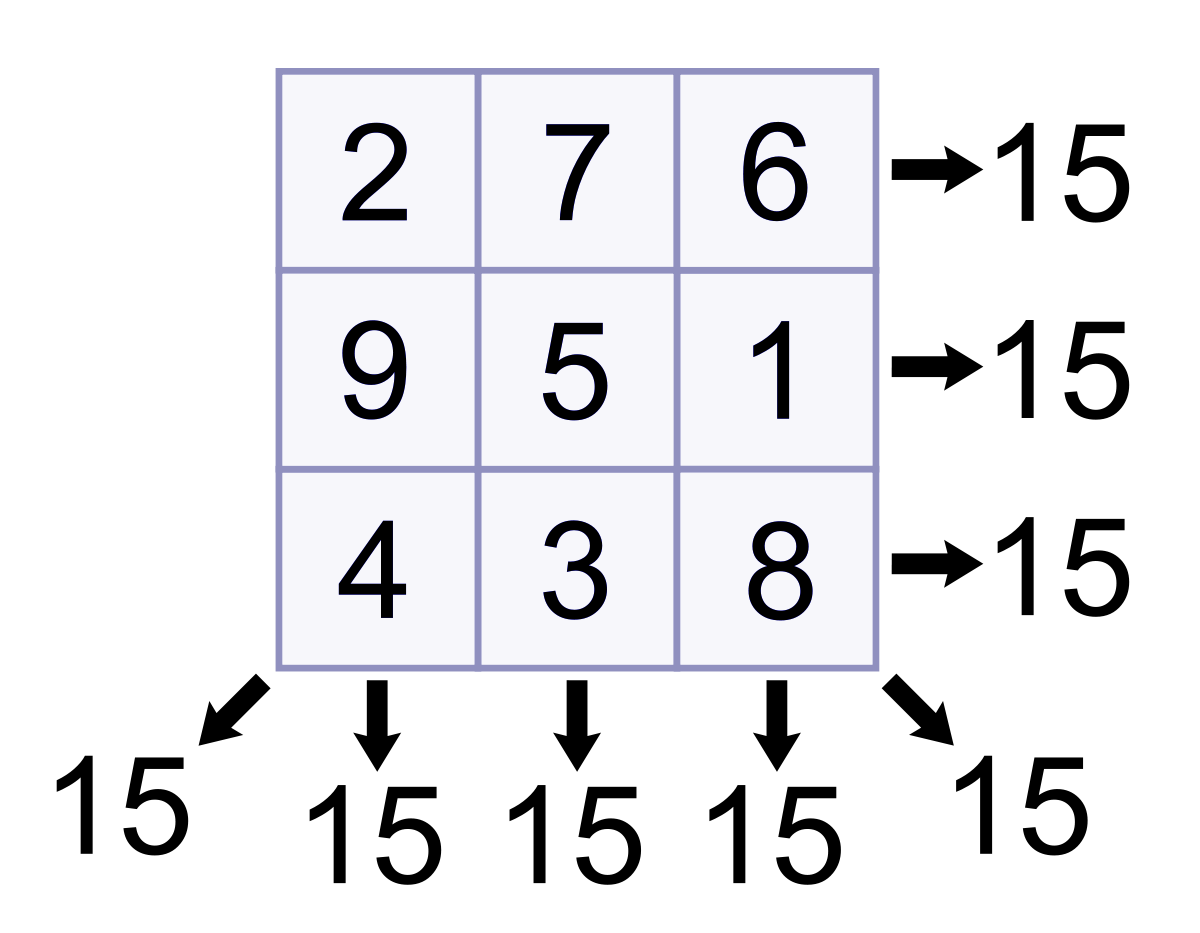
یک «مربع جادویی» یا «مربع وفقی» (Magic Square)، یک توالی از اعداد - معمولا صحیح - است که در یک مربع مشبک مرتب شده‌اند. در این مربع، مجموع اعداد هر سطر، هر ستون و هر قطر برابر با یک مقدار ثابت هستند که به آن «ثابت جادویی» (Magic Constant) گفته می‌شود. در ادامه، این روش با پایتون پیاده‌سازی می‌شود.

1def magic_square(matrix):
2   size=len(matrix[0])
3   sum_list=[]
4   for col in range(size): #Vertical sum
5       sum_list.append(sum(row[col] for row in matrix))
6   sum_list.extend([sum(lines) for lines in matrix])#Horizontal sum
7   result1=0
8   for i in range(0,size):
9       result1+=matrix[i][i]
10   sum_list.append(result1)
11   result2=0
12   for i in range(size-1,-1,-1):
13       result2+=matrix[i][i]
14   sum_list.append(result2)
15   if len(set(sum_list))>1:
16       return False
17   return True

در ادامه، این کد اجرا می‌شود:

1>>> magic_square([[1,2,3],[4,5,6],[7,8,9]])

غلط است. این یک مربع جادویی نیست. مجموع اعداد در هر سطر، ستون و قطر برابر با یک مقدار ثابت نیستند. در ادامه، یک لیست دیگر از لیست‌ها بررسی می‌شود.

1>>> magic_square([[2,7,6],[9,5,1],[4,3,8]])

درست است. با توجه به اینکه مجموع اعداد در همه جهت‌ها (سطرها، ستون‌ها و قطرها) برابر با ۱۵ می‌شود، لیست موجود یک مربع جادویی است.

جست و جوی هیوریستیک تبرید شبیه‌سازی شده

در «متالورژی» (Metallurgy)، هنگام سرد کردن فلزات به منظور رساندن آن‌ها به حالت انرژی پایین، فلز مقداری استحکام به دست می‌آورد. می‌توان این فرایند تبرید را شبیه‌سازی کرد. نظر به اینکه درجه حرارت بالا شاهد حرکات تصادفی بیشتری است، درجه حرارت پایین، حرکات تصادفی کمتری دارد.

فیلم آموزش شبیه سازی تبرید Simulated Annealing در متلب MATLAB در فرادرس

کلیک کنید

در هوش مصنوعی، از آنچه بیان شد برای تولید چیزی که تبرید شبیه‌سازی شده نام دارد، استفاده شده است. این کار، راهی برای بهینه‌سازی در هنگامی است که کار با جست و جوی تصادفی در درجه حرارت بالا آغاز می‌شود و سپس، درجه حرارت به آرامی کاهش پیدا می‌کند.

در نهایت، هنگامی که درجه حرارت به صفر می‌رسد، جست و جو به صورت «حریصانه نزولی خالص» (Pure Greedy Descent) می‌شود. در هر گام، این فرایند به صورت تصادفی یک متغیر و مقدار انتخاب می‌کند. در این روش، تخصیص‌ها تنها هنگامی پذیرفته شده‌اند که موجب بهبود وضعیت فعلی شوند و یا منجر به ناسازگاری (Conflict) بیشتر نشوند. در غیر این صورت، اگر دما نسبت به وضعیت کنونی بدتر شود (کاهش یا افزایش یابد)، تخصیص با یک احتمال مشخص قابل قبول خواهد بود.

یک برنامه تبرید نشان می‌دهد که درجه حرارت چگونه پیشرفت جست و جو را کاهش داده و قطع می‌کند. یک برنامه خیلی متداول در این راستا، «سرد کردن هندسی» (Geometric Cooling) است. اگر کار با درجه حرارت ۱۰ شروع شود و در هر گام درجه حرارت در 0.97 ضرب شود، پس از ۱۰۰ گام، نیاز به درجه حرارت ۰.۴۸ است.

جست و جوی هیوریستیک اول بهترین

جست و جوی اول بهترین، یک جست و جوی آگاهانه است که از یک تابع تکاملی برای تصمیم‌گیری پیرامون این موضوع استفاده می‌کند که کدام هم جوار مناسب‌ترین گزینه (امیدوار کننده‌ترین گزینه) پیش از ادامه اکتشاف محسوب می‌شود. جست و جوی اول عمق و اول سطح به صورت ناآگاهانه مسیرهایی را اکتشاف می‌کنند، بدون آنکه تابع هزینه را در نظر داشته باشند.

فیلم مجموعه آموزش هوش مصنوعی – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

اما موضوع در BFS متفاوت است. در اینجا، از یک صف اولویت برای ذخیره‌سازی هزینه گره‌ها استفاده می‌شود. در ادامه، برای درک بهتر الگوریتم اول بهترین، شبه کد آن ارائه شده است.

۱. لیست OPEN را با یک گره S - گره آغاز - تعریف کن

۲. اگر لیست خالی است، شکست را بازگردان

۳. گره n را (گره با بهترین امتیاز) را از لیست حذف کن، آن را به لیست CLOSED منتقل کن.

۴. گره n را بسط بده.

۵. اگر هر جانشینی برای n گره هدف است، موفقیت را بازگردان و مسیر را از گره هدف تا S به منظور باز گرداندن راهکار، ردیابی کن.

۶. برای هر گره جانشین:

• تابع ارزیابی f را اعمال کن.
• اگر گره در هیچ یک از لیست‌ها نیست، آن را به لیست OPEN اضافه کن.

۷. به گام ۲ حلقه بزن

جمع‌بندی

در این مطلب، روش‌های جست و جوی هیوریستیک در هوش مصنوعی مورد بررسی قرار گرفتند. در همین راستا، برخی از روش‌های این حوزه، شامل جست و جوی اول عمق، جست و جوی اول سطح، جست و جوی اول بهترین، جست و جوی *A، جست و جوی تپه نوردی، تبرید شبیه‌سازی شده و مسائل ارضای محدودیت معرفی شدند.

فیلم مجموعه آموزش داده کاوی و یادگیری ماشین – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

همچنین، به برخی از الگوریتم‌های بیان شده به صورت کامل‌تر پرداخته شد و الگوریتم مسائل ارضای محدودیت در پایتون پیاده‌سازی شد.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های الگوریتم ژنتیک و محاسبات تکاملی
• آموزش هوش مصنوعی
• مجموعه آموزش‌‌های هوش محاسباتی
• آموزش یادگیری ماشین با مثال‌‌های کاربردی
• فراگیری مفاهیم هوش مصنوعی — مجموعه مقالات جامع وبلاگ فرادرس
• معرفی منابع جهت آموزش یادگیری عمیق (Deep Learning) — راهنمای کامل
• درس هوش مصنوعی | مفاهیم پایه به زبان ساده — منابع، کتاب و فیلم آموزشی

^^